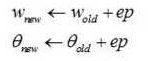深度学习入门

1.1 什么是学习？

  赫伯特·西蒙教授（Herbert Simon，1975年图灵奖获得者、1978年诺贝尔经济学奖获得者）曾对“学习”给了一个定义：“如果一个系统，能够通过执行某个过程，就此改进了它的性能，那么这个过程就是学习”

  学习的核心目的，就是改善性能。

1.2 什么是机器学习？

  对于某类任务（Task，简称T）和某项性能评价准则（Performance，简称P），如果一个计算机程序在T上，以P作为性能的度量，随着很多经验（Experience，简称E）不断自我完善，那么我们称这个计算机程序在从经验E中学习了

  对于一个学习问题，我们需要明确三个特征：任务的类型，衡量任务性能提升的标准以及获取经验的来源

1.3 学习的4个象限

1.4 机器学习的方法论

  “end-to-end”（端到端）说的是，输入的是原始数据（始端），然后输出的直接就是最终目标（末端），中间过程不可知，因此也难以知。

  就此，有人批评深度学习就是一个黑箱（Black Box）系统，其性能很好，却不知道为何而好，也就是说，缺乏解释性。其实，这是由于深度学习所处的知识象限决定的。从图1可以看出，深度学习，在本质上，属于可统计不可推理的范畴。“可统计”是很容易理解的，就是说，对于同类数据，它具有一定的统计规律，这是一切统计学习的基本假设。

  在哲学上讲，这种非线性状态，是具备了整体性的“复杂系统”，属于复杂性科学范畴。复杂性科学认为，构成复杂系统的各个要素，自成体系，但阡陌纵横，其内部结构难以分割。简单来说，对于复杂系统，1+1≠2，也就是说，一个简单系统，加上另外一个简单系统，其效果绝不是两个系统的简单累加效应，而可能是大于部分之和。因此，我们必须从整体上认识这样的复杂系统。于是，在认知上，就有了从一个系统或状态（end）直接整体变迁到另外一个系统或状态（end）的形态。这就是深度学习背后的方法论。

  “Divide and Conquer（分而治之）”，其理念正好相反，在哲学它属于“还原主义（reductionism，或称还原论）”。在这种方法论中，有一种“追本溯源”的蕴意包含其内，即一个系统（或理论）无论多复杂，都可以分解、分解、再分解，直到能够还原到逻辑原点。

  在意象上，还原主义就是“1+1=2”，也就是说，一个复杂的系统，都可以由简单的系统简单叠加而成（可以理解为线性系统），如果各个简单系统的问题解决了，那么整体的问题也就得以解决。

  经典机器学习（位于第Ⅱ象限），在哲学上，在某种程度上，就可归属于还原主义。传统的机器学习方式，通常是用人类的先验知识，把原始数据预处理成各种特征（feature），然后对特征进行分类。

  然而，这种分类的效果，高度取决于特征选取的好坏。传统的机器学习专家们，把大部分时间都花在如何寻找更加合适的特征上。故此，传统的机器学习，其实可以有个更合适的称呼——特征工程（feature engineering）。这也是有好处的，因为这些特征是由人找出来的，自然也就为人所能理解，性能好坏，可以灵活调整。

1.5 什么是深度学习？

  机器学习的专家们发现，可以让神经网络自己学习如何抓取数据的特征，这种学习的方式，效果更佳。于是兴起了特征表示学习（feature representation learning）的风潮。这种学习方式，对数据的拟合也更加的灵活好用。于是，人们终于从自寻“特征”的中解脱出来。

  但这种解脱也付出了代价，那就是机器自己学习出来的特征，它们存在于机器空间，完全超越了人类理解的范畴，对人而言，这就是一个黑盒世界。为了让神经网络的学习性能，表现得更好一些，人们只能依据经验，不断地尝试性地进行大量重复的网络参数调整。于是，“人工智能”领域就有这样的调侃：“有多少人工，就有多少智能”。

  再后来，网络进一步加深，出现了多层次的“表示学习”，它把学习的性能提升到另一个高度。这种学习的层次多了，就给它取了个特别的名称——Deep Learning（深度学习）。

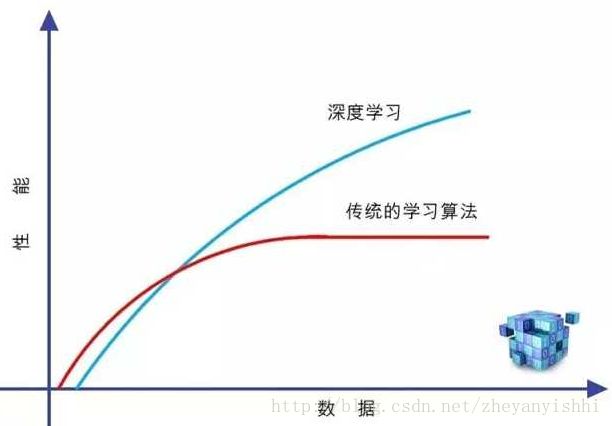
  深度学习的学习对象同样是数据。与传统机器学习所不同的是，它需要大量的数据，也就是“大数据（Big Data）”。

2.2 深度学习的归属

  把深度学习和传统的监督学习和无监督学习单列出来，自然是有一定道理的。这就是因为，深度学习是高度数据依赖型的算法，它的性能通常随着数据量的增加而不断增强，也就是说它的可扩展性（Scalability）显著优于传统的机器学习算法

  如果训练数据比较少，深度学习的性能并不见得就比传统机器学习好。其原因在于，作为复杂系统代表的深度学习算法，只有数据量足够多，才能通过训练，在深度神经网络中，将蕴含于数据之中的复杂模式表征出来。

机器学习要想做得好，需要走好三大步：

（1） 如何找一系列函数来实现预期的功能，这是建模问题；
（2） 如何找出一组合理的评价标准，来评估函数的好坏，这是评价问题；
（3） 如何快速找到性能最佳的函数，这是优化问题（比如说，机器学习中梯度下降法）。

2.4 为什么要用神经网络？

  深度学习的概念源于人工神经网络的研究。含多隐层的多层感知机就是一种深度学习结构。所以说到深度学习，就不能不提神经网络。

  “神经网络，是一种由具有自适应性的简单单元构成的广泛并行互联的网络，它的组织结构能够模拟生物神经系统对真实世界所作出的交互反应。”

那为什么要用神经网络学习呢？

  在人工智能领域，有两大主流。第一个是符号主义。符号主义的理念是，知识是信息的一种表达形式，人工智能的核心任务，就是处理好知识表示、知识推理和知识运用。核心方法论是，自顶向下设计规则，然后通过各种推理，逐步解决问题。很多人工智能的先驱（比如CMU的赫伯特•西蒙）和逻辑学家，很喜欢这种方法。但这个的发展，目前看来并不太好。

  还有一个就是试图编写一个通用模型，然后通过数据训练，不断改善模型中的参数，直到输出的结果符合预期，这个就是连接主义。连接主义认为，人的思维就是某些神经元的组合。因此，可以在网络层次上模拟人的认知功能，用人脑的并行处理模式，来表征认知过程。这种受神经科学的启发的网络，被称之人工神经网络（Artificial Neural Network，简称ANN）。这个网络的升级版，就是目前非常流行的深度学习。

  机器学习在本质就是寻找一个好用的函数。而人工神经网络最“牛逼”的地方在于，它可以在理论上证明：只需一个包含足够多神经元的隐藏层，多层前馈网络能以任意进度逼近任意复杂度的连续函数。这个定理也被称之为通用近似定理（Universal Approximation Theorem）。这里的“Universal”，也有人将其翻译成“万能的”，由此可见，这个定理的能量有多大。换句话说，神经网络可在理论上解决任何问题。

3.1 M-P神经元模型是什么？

  现在所讲的神经网络包括深度学习，都在某种程度上，都是在模拟大脑神经元的工作机理，它就是上世纪40年代提出但一直沿用至今的“M-P神经元模型”。

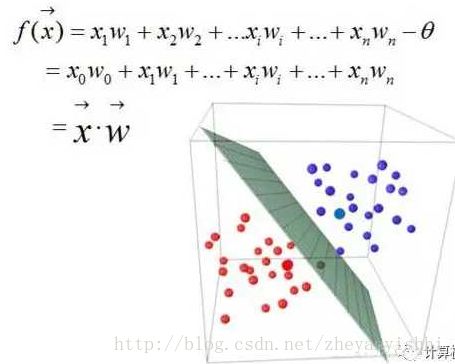
  在这个模型中，神经元接收来自n个其它神经元传递过来的输入信号，这些信号的表达，通常通过神经元之间连接的权重（weight）大小来表示，神经元将接收到的输入值按照某种权重叠加起来，并将当前神经元的阈值进行比较，然后通过“激活函数（activation function）”向外表达输出（这在概念上就叫感知机）。

3.3 激活函数是怎样的一种存在？

  神经元的工作模型存在“激活（1）”和“抑制（0）”等两种状态的跳变，那么理想型的激活函数（activation functions）就应该是阶跃函数，但这种函数具有不光滑、不连续等众多不“友好”的特性。为什么说它“不友好”呢，这是因为在训练网络权重时，通常依赖对某个权重求偏导、寻极值，而不光滑、不连续等通常意味着该函数无法“连续可导”。

  因此，我们通常用Sigmoid函数来代替阶跃函数。这个函数可以把较大变化范围内输入值（x）挤压输出在（0,1）范围之内，故此这个函数又称为“挤压函数（Squashing function）”。

3.4 卷积函数又是什么？

  所谓卷积，就是一个功能和另一个功能在时间的维度上的“叠加”作用。

  由卷积得到的函数h一般要比f和g都光滑。利用这一性质，对于任意的可积函数f，都可简单地构造出一列逼近于f的光滑函数列，这种方法被称之为函数的光滑化或正则化。

  在时间的维度上的“叠加作用”，如果函数是离散的，就用求累积和来刻画。如果函数是连续的，就求积分来表达。

4.1机器学习的三个层次

大致可分为三类：

（1）监督学习（Supervised Learning）:
  监督学习基本上就是“分类（classification）”的代名词。它从有标签的训练数据中学习，然后给定某个新数据，预测它的标签（given data, predict labels）。
  简单来说，监督学习的工作，就是通过有标签的数据训练，获得一个模型，然后通过构建的模型，给新数据添加上特定的标签。
  整个机器学习的目标，都是使学习得到的模型，能很好地适用于“新样本”，而不是仅仅在训练样本上工作得很好。通过训练得到的模型，适用于新样本的能力，称之为“泛化（generalization）能力”。

（2）非监督学习（Unsupervised Learning）：
  与监督学习相反的是，非监督学习所处的学习环境，都是非标签的数据。非监督学习，本质上，就是“聚类（cluster）”的近义词。
  简单来说，给定数据，从数据中学，能学到什么，就看数据本身具备什么特性（given data, learn about that data）。我们常说的“物以类聚，人以群分”说得就是“非监督学习”。这里的“类”也好，“群”也罢，事先我们是不知道的。一旦我们归纳出“类”或“群”的特征，如果再要来一个新数据，我们就根据它距离哪个“类”或“群”较近，就“预测”它属于哪个“类”或“群”，从而完成新数据的“分类”或“分群”功能。

（3）半监督学习（Semi-supervised Learning）：
  这类学习方式，既用到了标签数据，又用到了非标签数据。
  给定一个来自某未知分布的有标记示例集L={(x1, y1), (x2, y2), …, (xl, yl)}，其中xi是数据，yi是标签。对于一个未标记示例集U = {xl+1, x l+1, … , xl+u}，I《u，于是，我们期望学得函数 f:X→Y 可以准确地对未标识的数据xi预测其标记yi。这里均为d维向量, yi∈Y为示例xi的标记。
  半监督学习就是以“已知之认知（标签化的分类信息）”，扩大“未知之领域（通过聚类思想将未知事物归类为已知事物）”。但这里隐含了一个基本假设——“聚类假设（cluster assumption）”，其核心要义就是：“相似的样本，拥有相似的输出”。

5.2 认识“感知机”

  所谓的感知机，其实就是一个由两层神经元构成的网络结构，它在输入层接收外界的输入，通过激活函数（含阈值）的变换，把信号传送至输出层，因此它也称之为“阈值逻辑单元（threshold logic unit）”。

  所有“有监督”的学习，在某种程度上，都是分类（classification）学习算法。而感知机就是有监督的学习，所以，它也是一种分类算法。

5.3 感知机是如何学习的？

  对象本身的特征值，一旦确定下来就不会变化。因此，所谓神经网络的学习规则，就是调整权值和阈值的规则（这个结论对于深度学习而言，依然是适用的）。

假设我们的规则是这样的：

其中ep = y- y’，y为期望输出，y’是实际输出，所以，具体说来，ep是二者的差值。

5.4 感知机的训练法则

  感知机的学习规则：对于训练样例（x，y）（需要注意的是，这里粗体字x表示训练集合），若当前感知机的实际输出y’，假设它不符合预期，存在“落差”，那么感知机的权值依据如公式规则调整：

其中，η∈(0,1)称为学习率(learning rate)

  这里需要注意的是，学习率η的作用是“缓和”每一步权值调整强度的。它本身的大小，也是比较难以确定的。如果η太小，网络调参的次数就太多，从而收敛很慢。如果η太大，容易错过了网络的参数的最优解。因此，合适的η大小，在某种程度上，还依赖于人工经验。

5.5 感知机的表征能力

  1969年，马文·明斯基和西摩尔· 派普特（Seymour Papert）在出版了《感知机：计算几何简介”》一书[2], 书中论述了感知机模型存在的两个关键问题：
（1）单层的神经网络无法解决不可线性分割的问题，典型例子如异或门电路（XOR Circuit）；
（2）更为严重的问题是，即使使用当时最先进的计算机，也没有足够计算能力，完成神经网络模型所需要的超大的计算量（比如调整网络中的权重参数）。
  鉴于明斯基的江湖地位（1969年刚刚获得大名鼎鼎的图灵奖），他老人家一发话不要紧，直接就把人工智能的研究，送进一个长达近二十年的低潮，史称“人工智能冬天（AI Winter）”。

6.1 复杂网络解决“异或”问题

  感知机之所以当初无法解决“非线性可分”问题，是因为相比于深度学习这个复杂网络，感知机太过于简单”。

  想解决“异或”问题，就需要使用多层网络。这是因为，多层网络可以学习更高层语义的特征，其特征表达能力更强。因此，我们在输入层和输出层之间，添加一层神经元，将其称之为隐含层（“隐层”）。于是隐层和输出层中的神经元都有激活函数。

  1958年Frank Rosenblatt提出感知机的概念。1965年Alexey Grigorevich Ivakhnenko提出了多层人工神经网络的设想。而这种基于多层神经网络的机器学习模型，后来被人们称为“深度学习”。

6.2 多层前馈神经网络

  常见的多层神经网络如图所示。在这种结构中，每一层神经元仅仅与下一层的神经元全连接。而在同一层，神经元彼此不连接，而且跨层的神经元，彼此间也不相连。这种被简化的神经网络结构，被称之为“多层前馈神经网络（multi-layer feedforward neural networks）”。

  在多层前馈神经网络中，输入层神经元主要用于接收外加的输入信息，在隐含层和输出层中，都有内置的激活函数，可对输入信号进行加工处理，最终的结果，由输出层“呈现”出来。

  这里需要说明的是，神经元中的激活函数，并不限于我们前面提到的阶跃函数、Sigmod函数，还可以是现在深度学习常用的ReLU（Rectified Linear Unit）和sofmax等。

  简单来说，神经网络的学习过程，就是通过根据训练数据，来调整神经元之间的连接权值（connection weight）以及每个功能神经元的输出阈值。换言之，神经网络需要学习的东西，就蕴含在连接权值和阈值之中。

6.3 误差逆传播算法

  对于相对复杂的前馈神经网络，其各个神经元之间的链接权值和其内部的阈值，是整个神经网络的灵魂所在，它需要通过反复训练，方可得到合适的值。而训练的抓手，就是实际输出值和预期输出值之间存在着“误差”。

  在机器学习中的“有监督学习”算法里，在假设空间中，构造一个决策函数f，对于给定的输入X，由f(X)给出相应的输出Y，这个实际输出值Y和原先预期值Y’可能不一致。于是，我们需要定义一个损失函数（loss function），也有人称之为代价函数（cost function）来度量这二者之间的“落差”程度。这个损失函数通常记作L(Y,Y)= L(Y, f(X))，为了方便起见，这个函数的值为非负数（请注意：这里的大写Y和Y’，分别表示的是一个输出值向量和期望值向量，它们分别包括多个不同对象的实际输出值和期望值）。

常见的损失函数有如下3类：

  损失函数值越小，说明实际输出和预期输出的差值就越小，也就说明我们构建的模型越好。

  神经网络学习的本质，其实就是利用“损失函数（loss function）”，来调节网络中的权重（weight）。

  调神经网络的权值，有两大类方法比较好使。第一种方法就是“误差反向传播（Error Back propagation，简称BP）”。简单说来，就是首先随机设定初值，然后计算当前网络的输出，然后根据网络输出与预期输出之间的差值，采用迭代的算法，反方向地去改变前面各层的参数，直至网络收敛稳定。

  BP算法非常经典，在很多领域都有着经典的应用，当时它的火爆程度在绝不输给现在的“深度学习”。但后来大家发现，实际用起来它还是有些问题。比如说，在一个层数较多网络中，当它的残差反向传播到最前面的层（即输入层），其影响已经变得非常之小，甚至出现梯度扩散（gradient-diffusion），严重影响训练精度。

  再后来，第二类改进方法就孕育而生了。它就是当前主流的方法，也就是“深度学习”常用的“逐层初始化”(layer-wise pre-training)训练机制，不同于BP的“从后至前”的训练参数方法，“深度学习”采取的是一种从“从前至后”的逐层训练方法。

7.3到底什么是梯度？

  在单变量的实值函数中，梯度就可以简单地理解为只是导数，或者说对于一个线性函数而言，梯度就是线的斜率。但对于多维变量的函数，它的梯度概念就不那么容易理解了。

  在向量微积分中，标量场的梯度其实是一个向量场（vector field）。对于特定函数的某个特定点，它的梯度就表示从该点出发，该函数值增长最为迅猛的方向（direction of greatest increase of a function）。

  梯度最明显的应用，就是快速找到多维变量函数的极(大/小)值。

  “梯度递减”的问题所在，那就是它很容易收敛到局部最小值。

7.5 重温神经网络的损失函数

  相比于神经网络输入、输出层设计的简单直观，它的隐含层设计，可就没有那么简单了。依赖于“工匠”的打磨，它就是一个体力活，需要不断地“试错”。

  但通过不断地“折腾”，研究人员掌握了一些针对隐层的启发式设计规则（如下文即将提到的BP算法），以此降低训练网络所花的开销，并尽量提升网络的性能。

  为了达到理想状态，我们希望快速配置好网络参数，从而让这个损失函数达到极小值。这时，神经网络的性能也就接近最优！

8.1 BP神经网络

BP算法，是一个典型的双向算法。更确切来说，它的工作流程是分两大步走：
  （1）正向传播输入信号，输出分类信息（对于有监督学习而言，基本上都可归属于分类算法）；
  （2）反向传播误差信息，调整全网权值（通过微调网络参数，让下一轮的输出更加准确）。

8.2.1正向传播信息
  类似于感知机，每一个神经元的功能都可细分两大部分：（1）汇集各路链接带来的加权信息；（2）加权信息在激活函数的“加工”下，神经元给出相应的输出

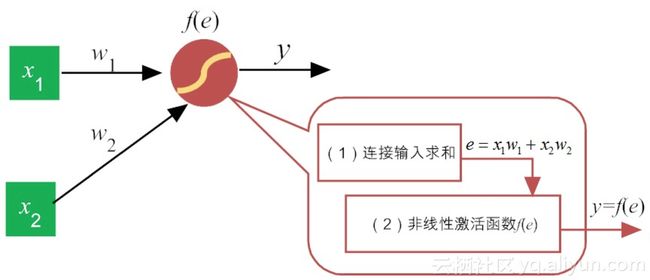
  到第一轮信号前向传播的输出值计算出来后，实际输出向量与预期输出的向量之间的误差就可计算出来。下面我们就用“误差”信息反向传播，来逐层调整网络参数。为了提高权值更新效率，这里就要用到下文即将提到的“反向模式微分法则（chain rule）”。

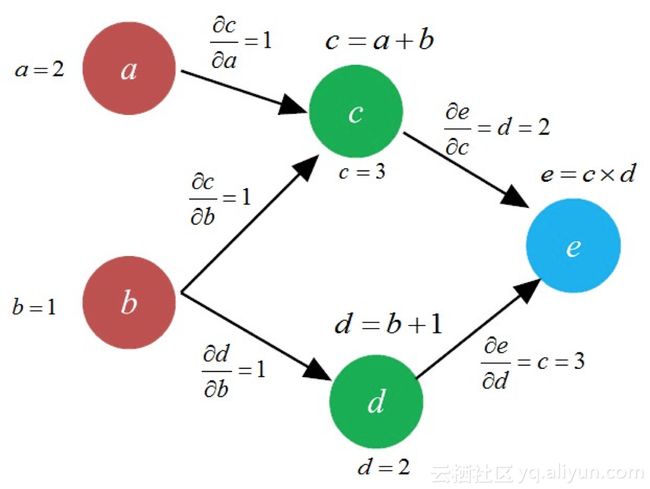
8.2.2 求导中的链式法则

一般化的神经网络示意图：

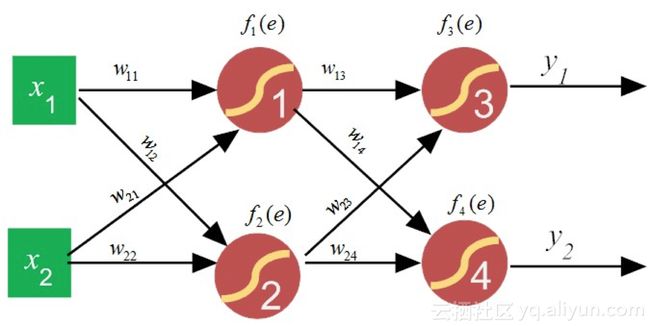
  为了简化理解，暂时假设神经元没有激活函数（或称激活函数为y=xy=x），于是对于隐含层神经元，它的输出可分别表示为：
        
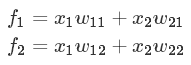
  然后，对于输出层神经元有：
        
  于是，损失函数 L 可表示为公式：
        
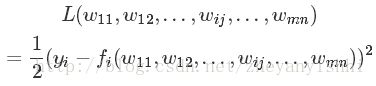
  这里 Y 为预期输出值向量(由 y1,y2,...,yi,... 等元素构成)，实际输出向量为 fi(w11,w12,...,wij,...,wmn) 。
  对于有监督学习而言，在特定训练集合下，输入元素 xi 和预期输出 yi 都可视为常量。由此可以看到，损失函数 L ，在本质上，就是一个单纯与权值 wij 相关的函数（即使把原本的激活函数作用加上去，除了使得损失函数的形式表现得更加复杂外，并不影响这个结论）。
  于是，损失函数 L 梯度向量可表示为公式：
        
其中，这里的 eij 是正交单位向量。为了求出这个梯度，需要求出损失函数 L 对每一个权值 wij 的偏导数。

链式求导示例图：

---

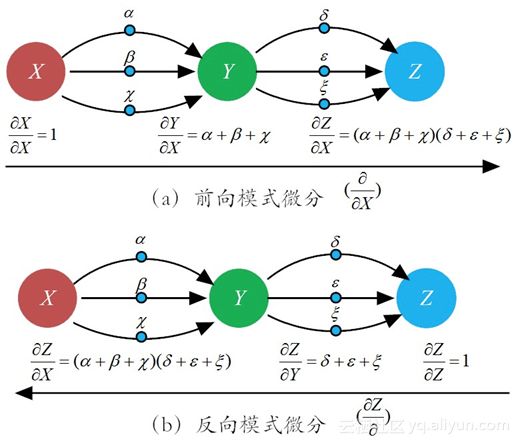
  当网络结构简单时，即使 X 到 Z 的每一个路径都使用前向模式微分（forward-mode differentiation）”，也不会有很多路径，但一旦网络结构的复杂度上去了，这种“前向模式微分”，就会让求偏导数的次数和神经元个数的平方成正比。这个计算量，就很可能是成为机器“难以承受的计算之重”。

  为了避免这种海量求导模式，数学家们另辟蹊径，提出了一种称之为“反向模式微分（reverse-mode differentiation）”。取代之前的简易的表达方式，我们用下面的公式的表达方式来求 X 对 Z 的偏导：
        

  前向模式微分方法，其实就是我们在高数课堂上学习的求导方式。在这种求导模式中，强调的是某一个输入（比如 X ）对某一个节点（如神经元）的影响。因此，在求导过程中，偏导数的分子部分，总是根据不同的节点总是不断变化，而分母则锁定为偏导变量“ ∂X ”，保持定不变。

  反向模式微分方法则有很大不同。首先在求导方向上，它是从输出端（output）到输入端进行逐层求导。其次，在求导方法上，它不再是对每一条“路径”加权相乘然后求和，而是针对节点采纳“合并同类路径”和“分阶段求解”的策略。先求 Y 节点对 Z 节点的”总影响”（反向第一层），然后，再求节点 X 对节点 Z 的总影响（反向第二层）。

  特别需要注意的是， ∂Z/∂Y 已经在第一层求导得到。在第二层仅仅需要求得 ∂Y/∂X ，然后二者相乘即可得到所求。这样一来，就大大减轻了第二层的求导负担。在求导形式上，偏导数的分子部分（节点）不变，而分母部分总是随着节点不同而变化。

  利用链式法则，反向模式微分方法就能避免冗余对所有路径只求一次导数，大大加快了运行速度！BP算法把网络权值纠错的运算量,从原来的与神经元数目的平方成正比，下降到只和神经元数目本身成正比。其功劳，正是得益于这个反向模式微分方法节省的计算冗余。

8.2.3 误差反向传播

  误差反向传播通过梯度下降算法，迭代处理训练集合中的样例，一次处理一个样例。对于样例 d ，如果它的预期输出和实际输出有“误差”，BP算法抓住这个误差信号 Ld ，以“梯度递减”的模式修改权值。也就是说，对于每个训练样例 d ，权值 wji 的校正幅度为 Δwji （需要说明的是， wji 和 wij 其实都是同一个权值， wji 表示的是神经元 j 的第 i 个输入相关的权值，这里之所以把下标“ j ”置于“ i ”之前，仅仅表示这是一个反向更新过程而已）：
        
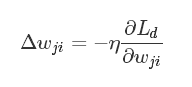
  在这里， Ld 表示的是训练集合中样例 d 的误差，分解到输出层的所有输出向量， Ld 可表示为：
        
其中：
yj 表示的是第 j 个神经单元的预期输出值。
y'j 表示的 j 个神经单元的实际输出值。
outputs 的范围是网络最后一层的神经元集合。

  下面我们推导出 ∂Ld/∂wji 的一个表达式，以便在上面的公式中使用梯度下降规则。
  首先，我们注意到，权值 wji 仅仅能通过 netj 影响其他相连的神经元。因此利用链式法则有：
        
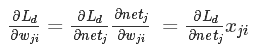
在这里， netj=∑iwjixji ，也就是神经元 j 输入的加权和。 xji 表示的神经 j 的第 i 个输入。需要注意的是，这里的 xji 是个统称，实际上，在反向传播过程中，在经历输出层、隐含层和输入层时，它的标记可能有所不同。

  由于在输出层和隐含层的神经元对“纠偏”工作，承担的“责任”是不同的，至少是形式不同，所以需要我们分别给出推导。
（1）在输出层，对第 i 个神经元而言，省略部分推导过程，上一公式的左侧第一项为：
        
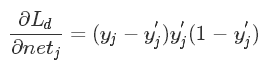
  为了方便表达，我们用该神经元的纠偏“责任（responsibility）” δ(1)j 描述这个偏导，即：
        
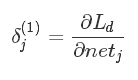
  这里 δ(1)j 的上标“(1)”，表示的是第1类（即输出层）神经元的责任。如果上标为“(2)”，则表示第2类（即隐含层）神经元的责任，见下面的描述。
（2）对隐含层神经元jj的梯度法则（省略了部分推导过程），有：
        
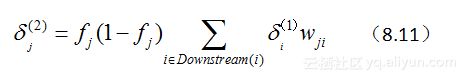
其中：
   fj 表示神经单元jj的计算输出。
   netj 表示的是神经单元jj的加权之和。
   Downstream(j) 表示的是在网络中神经单元jj的直接下游单元集合。

  在明确了各个神经元“纠偏”的职责之后，下面就可以依据类似于感知机学习，通过如下加法法则更新权值：
对于输出层神经元有：
        
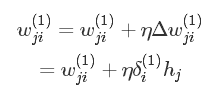
对于隐含层神经元有：
        
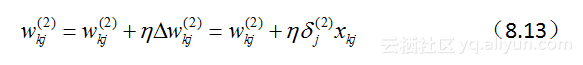
在这里， η∈(0,1) 表示学习率。在实际操作过程中，为了防止错过极值， η 通常取小于0.1的值。 hj 为神经元j的输出。 xjk 表示的是神经单元 j 的第 k 个输入。

题外话：
LeCun成功应用BP神经网络在手写邮编识别之后，与LeCun同在一个贝尔实验室的同事Vladimir Vapnik（弗拉基米尔·万普尼克），提出并发扬光大了支持向量机 (Support Vector Machine) 算法。
SVM作为一种分类算法，对于线性分类，自然不在话下。在数据样本线性不可分时，它使用了所谓“核机制(kernel trick)”，将线性不可分的样本，映射到高维特征空间 (high-dimensional feature space)，从而使其线性可分。自上世纪九十年代初开始，SVM在图像和语音识别等领域，获得了广泛而成功的应用。
在手写邮政编码的识别问题上，LeCun利用BP算法，把错误率整到5%左右，而SVM在1998年就把错误率降到低至0.8%。这远超越同期的传统神经网络算法。
就这样，万普尼克又把神经网络研究送到了一个新的低潮！