为什么研究彩票是一种“侮辱智商”的行为?
你有没有在买股票、期货、彩票的时候,在连续好几把上来就亏损的情况下,是不是觉得下一把挣钱的概率很大?
你有没有有过这样的妄想,希望少干活多挣钱,甚至不干活光挣钱。
有这样想法的人当中,有少数人会去做两件事:研究彩票如何中奖,赌博。
这里说的赌博,可不只是去赌场,还包括每天研究各种K线图来预测股票价格的。这类人最长的谈资往往是这样的:
“已经涨了这么久了,下次该跌了吧?”
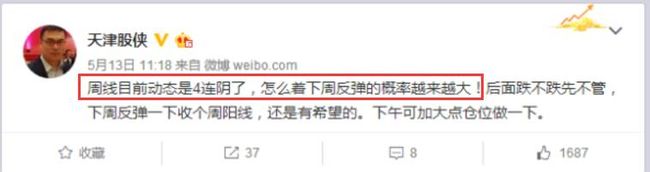
“这只股票已经连续跌了1周了,所以下周反弹的概率越来越多。”
这样的人不在少数,包括下面这位在微博上有255万粉丝的红人“天津股侠”。
而且越是窘迫的时候,他们越容易采取这种极端方式,希望自己成为那极少数的幸运儿。但结果往往是连最后翻身的资本都没有了。
如果你今天学习了概率思维给我们的第1个智慧:赌徒谬论,就会知道这样的举动有多么的“侮辱智商”。
概率其实最早就来自于赌博。法国数学家帕斯卡一个喜欢赌博的朋友遇到个问题请教他:兄弟,我赌掷三个骰子出现某种组合时为什么老是输钱?
帕斯卡 于是就通过信件和他的好基友 费马 对这个问题进行了讨论。这一讨论不要紧,引发他们提出了一些概率论的原理,从而创立了概率论。
回到正题上来,
“赌徒谬误”(Gambler's Fallacy),指的是:
绝大多数赌徒倾向于相信 之前的下注结果对当前下注有影响。
这是什么意思呢?
假如你在赌场玩纸牌,一上来运气不太好,连输好几把。这时候你是否有种强烈的感觉,你很快该赢了?
买股票、期货、彩票都是一样。连续好几把上来就亏损的情况下,是不是觉得下一把挣钱的概率很大?这就是赌徒谬论。
其实,这完全是一种错觉。
赌博完全是独立的随机事件,这意味着下一把的结果和以前所有的结果都没有任何联系,已经发生了的事情不会影响将来。
赌徒之所以是赌徒,其实就是知识欠缺,他们无力理解和接受概率学上的那个重要概念:“独立事件”。
在概率中事件有两种类型:独立事件,相关事件。今天我们先来看看什么是独立事件。
独立事件是不受过去事件影响的。
如何理解这句话呢?
如果A和B是独立事件,则A的结果对B的结果没有影响,同时B的结果对A的结果没有影响。
也就是A和B各自的结果对对方没有影响。所以独立事件不会影响对方的概率。
例如抛硬币就是独立事件,硬币不“知道”它以前曾经正面向上还是向下。每一次抛掷硬币都是个绝对独立的事件,所以不管你抛一个硬币2次,还是3次,每次正面向上的概率都是50% 。
很多时候,了解多个事件同时发生的概率是很有价值的。例如某小区停电且备用发电机失灵的可能性有多大。
如果事件A和B是独立事件,A和B同时发生的概率等于A 的概率乘以B 的概率。
举个例子可能会更直观一些。
你抛一个硬币三次,结果全是"正面"的概率是多少?
抛一枚标准硬币得到正面朝上的概率为1/2,连续抛两次都得到正面朝上的概率为1/2×1/2=1/4,连续抛3次都得到正面朝上的概率为1/8
有些人可能想:“已经三次正面了,这一次应该轮到反面了吧”,但无论如可,下一次抛掷与以前的抛掷是完全独立的,概率还是1/2。
同样的,那些说“这只股票已经连续跌了1周了,所以下周反弹的概率越来越多。” 也是因为不理解独立事件常识。最终导致的结果,就是成为“韭菜”。
有个笑话说一个人乘坐飞机时总带着一颗炸弹,他认为这样就不会被恐怖分子炸飞机了,因为一架飞机上有两颗炸弹的可能性非常小。
战场上士兵有个说法,如果战斗中炸弹在你身边爆炸,你应该迅速跳进那个弹坑,因为两颗炸弹不大可能打到同一个地方。
这都是不理解独立事件导致的。
1.什么是赌徒谬论?
赌徒谬论是说:绝大多数赌徒倾向于相信之前的下注结果对当前下注有影响。
这种错误的认知是因为人们不了解什么是独立事件。
常见的错误行为有:研究彩票中奖,短期看K线图预测股价。
2.什么是独立事件?
独立事件是不受过去事件影响的事件。例如抛硬币。
3.如何计算多个独立事件的概率?
如果事件A和B是独立事件,A和B同时发生的概率等于A 的概率乘以B 的概率。
有统计表明,无论学没学过概率,真正不受“赌徒谬误”影响的人,低于总人口比例的20%,也就是说,至少有80% 的人或多或少会受“赌徒谬误”影响——别震惊,事实如此。
相信你通过今天的知识,现在已经摆脱了赌徒谬论的错误思维。
如果你是为了碰运气,撞大运,偶尔买下彩票是可以的,但是花大力气研究彩票中奖,还是洗洗睡吧。有这时间倒不如学点统计概率知识提高下认知。
![]()