tensorflow 2.0 深度学习(第一部分 part1)
日萌社
人工智能AI:Keras PyTorch MXNet TensorFlow PaddlePaddle 深度学习实战(不定时更新)
tensorflow 2.0 深度学习(第一部分 part1)
tensorflow 2.0 深度学习(第一部分 part2)
tensorflow 2.0 深度学习(第一部分 part3)
tensorflow 2.0 深度学习(第二部分 part1)
tensorflow 2.0 深度学习(第二部分 part2)
tensorflow 2.0 深度学习(第二部分 part3)
tensorflow 2.0 深度学习 (第三部分 卷积神经网络 part1)
tensorflow 2.0 深度学习 (第三部分 卷积神经网络 part2)
tensorflow 2.0 深度学习(第四部分 循环神经网络)
tensorflow 2.0 深度学习(第五部分 GAN生成神经网络 part1)
tensorflow 2.0 深度学习(第五部分 GAN生成神经网络 part2)
tensorflow 2.0 深度学习(第六部分 强化学习)
综合
CPU 和 GPU 的运算时间区别
加速计算
神经网络本质上由大量的矩阵相乘,矩阵相加等基本数学运算构成,TensorFlow 的重
要功能就是利用 GPU 方便地实现并行计算加速功能。为了演示 GPU 的加速效果,我们通
过完成多次矩阵 A 和矩阵 B 的矩阵相乘运算的平均运算时间来验证。其中矩阵 A 的 shape
为[1,],矩阵 B 的 shape 为[, 1],通过调节 n 即可控制矩阵的大小。
首先我们分别创建使用 CPU 和 GPU 运算的 2 个矩阵:
import tensorflow as tf
import timeit
n = 10
# 创建在 CPU 上运算的 2 个矩阵
with tf.device('/cpu:0'):
cpu_a = tf.random.normal([1, n])
cpu_b = tf.random.normal([n, 1])
print(cpu_a.device, cpu_b.device)
# 创建使用 GPU 运算的 2 个矩阵
with tf.device('/gpu:0'):
gpu_a = tf.random.normal([1, n])
gpu_b = tf.random.normal([n, 1])
print(gpu_a.device, gpu_b.device)
#通过 timeit.timeit()函数来测量 2 个矩阵的运算时间:
def cpu_run():
with tf.device('/cpu:0'):
print(cpu_a, cpu_b)
c = tf.matmul(cpu_a, cpu_b)
return c
def gpu_run():
with tf.device('/gpu:0'):
print(cpu_a, cpu_b)
c = tf.matmul(gpu_a, gpu_b)
return c
# 第一次计算需要热身,避免将初始化阶段时间结算在内
cpu_time = timeit.timeit(cpu_run, number=10)
gpu_time = timeit.timeit(gpu_run, number=10)
print('warmup:', cpu_time, gpu_time)
# 正式计算 10 次,取平均时间
cpu_time = timeit.timeit(cpu_run, number=10)
gpu_time = timeit.timeit(gpu_run, number=10)
print('run time:', cpu_time, gpu_time)
我们将不同大小的 n 下的 CPU 和 GPU 的运算时间绘制为曲线,如图 1.21 所示。可以看
到,在矩阵 A 和 B 较小时,CPU 和 GPU 时间几乎一致,并不能体现出 GPU 并行计算的
优势;在矩阵较大时,CPU 的计算时间明显上升,而 GPU 充分发挥并行计算优势,运算
时间几乎不变。
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
# Default parameters for plots
matplotlib.rcParams['font.size'] = 20
matplotlib.rcParams['figure.titlesize'] = 20
matplotlib.rcParams['figure.figsize'] = [9, 7]
matplotlib.rcParams['font.family'] = ['STKaiti']
matplotlib.rcParams['axes.unicode_minus']=False
import tensorflow as tf
import timeit
cpu_data = []
gpu_data = []
for n in range(9):
n = 10**n
# 创建在CPU上运算的2个矩阵
with tf.device('/cpu:0'):
cpu_a = tf.random.normal([1, n])
cpu_b = tf.random.normal([n, 1])
print(cpu_a.device, cpu_b.device)
# 创建使用GPU运算的2个矩阵
with tf.device('/gpu:0'):
gpu_a = tf.random.normal([1, n])
gpu_b = tf.random.normal([n, 1])
print(gpu_a.device, gpu_b.device)
def cpu_run():
# 创建在CPU上运算的2个矩阵
with tf.device('/cpu:0'):
c = tf.matmul(cpu_a, cpu_b)
return c
def gpu_run():
# 创建使用GPU运算的2个矩阵
with tf.device('/gpu:0'):
c = tf.matmul(gpu_a, gpu_b)
return c
# 第一次计算需要热身,避免将初始化阶段时间结算在内
cpu_time = timeit.timeit(cpu_run, number=10)
gpu_time = timeit.timeit(gpu_run, number=10)
print('warmup:', cpu_time, gpu_time)
# 正式计算10次,取平均时间
cpu_time = timeit.timeit(cpu_run, number=10)
gpu_time = timeit.timeit(gpu_run, number=10)
print('run time:', cpu_time, gpu_time)
cpu_data.append(cpu_time/10)
gpu_data.append(gpu_time/10)
del cpu_a,cpu_b,gpu_a,gpu_b
x = [10**i for i in range(9)]
cpu_data = [1000*i for i in cpu_data]
gpu_data = [1000*i for i in gpu_data]
plt.plot(x, cpu_data, 'C1')
plt.plot(x, cpu_data, color='C1', marker='s', label='CPU')
plt.plot(x, gpu_data,'C0')
plt.plot(x, gpu_data, color='C0', marker='^', label='GPU')
plt.gca().set_xscale('log')
plt.gca().set_yscale('log')
plt.ylim([0,100])
plt.xlabel('矩阵大小n:(1xn)@(nx1)')
plt.ylabel('运算时间(ms)')
plt.legend()
plt.savefig('gpu-time.svg')
import tensorflow as tf
# 创建4个张量
a = tf.constant(1.)
b = tf.constant(2.)
c = tf.constant(3.)
w = tf.constant(4.)
with tf.GradientTape() as tape:# 构建梯度环境
tape.watch([w]) # 将w加入梯度跟踪列表
# 构建计算过程
y = a * w**2 + b * w + c
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
[dy_dw] = tape.gradient(y, [w])
print(dy_dw)
import tensorflow as tf
x = tf.constant(1.)
a = tf.constant(2.)
b = tf.constant(3.)
c = tf.constant(4.)
# 构建梯度环境
with tf.GradientTape() as tape:
# 将a, b, c加入梯度跟踪列表
tape.watch([a, b, c])
# 构建计算过程
y = a**2 * x + b * x + c
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
[dy_da, dy_db, dy_dc] = tape.gradient(y, [a, b, c])
print(dy_da, dy_db, dy_dc)
conv_train.py
import os
import time
import numpy as np
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # or any {'0', '1', '2'}
import tensorflow as tf
from tensorflow.python.ops import summary_ops_v2
from tensorflow import keras
from tensorflow.keras import datasets, layers, models, optimizers, metrics
model = tf.keras.Sequential([
layers.Reshape(
target_shape=[28, 28, 1],
input_shape=(28, 28,)),
layers.Conv2D(2, 5, padding='same', activation=tf.nn.relu),
layers.MaxPooling2D((2, 2), (2, 2), padding='same'),
layers.Conv2D(4, 5, padding='same', activation=tf.nn.relu),
layers.MaxPooling2D((2, 2), (2, 2), padding='same'),
layers.Flatten(),
layers.Dense(32, activation=tf.nn.relu),
layers.Dropout(rate=0.4),
layers.Dense(10)])
compute_loss = tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True) #计算loss = compute_loss(真实标签labels, 预测输出logits标签)
compute_accuracy = tf.keras.metrics.SparseCategoricalAccuracy() #计算准确率accuracy = compute_accuracy(真实标签labels, 预测输出logits标签)
optimizer = optimizers.SGD(learning_rate=0.01, momentum=0.5) #SGD随机梯度下降
def mnist_datasets():
(x_train, y_train), (x_test, y_test) = datasets.mnist.load_data()
# Numpy defaults to dtype=float64; TF defaults to float32. Stick with float32.
x_train, x_test = x_train / np.float32(255), x_test / np.float32(255) #标准化/归一化
y_train, y_test = y_train.astype(np.int64), y_test.astype(np.int64)
train_dataset = tf.data.Dataset.from_tensor_slices((x_train, y_train)) #构建数据集用于按照批量大小进行遍历
test_dataset = tf.data.Dataset.from_tensor_slices((x_test, y_test))
return train_dataset, test_dataset
train_ds, test_ds = mnist_datasets()
train_ds = train_ds.shuffle(60000).batch(100) #shuffle打乱样本数据顺序,然后数据集中的按照批量大小构建
test_ds = test_ds.batch(100)
def train_step(model, optimizer, images, labels):
# Record the operations used to compute the loss, so that the gradient
# of the loss with respect to the variables can be computed.
#构建梯度记录环境
with tf.GradientTape() as tape:
logits = model(images, training=True)#输入数据到模型中训练,预测输出logits标签
loss = compute_loss(labels, logits) #根据预测输出logits标签和真实标签labels,计算loss两者之间的误差值
compute_accuracy(labels, logits) #根据预测输出logits标签和真实标签labels,计算accuracy两者之间的准确率
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
grads = tape.gradient(loss, model.trainable_variables)
#优化器规则,根据 模型参数θ = θ - lr * grad 更新网络参数
optimizer.apply_gradients(zip(grads, model.trainable_variables))
return loss
def train(model, optimizer, dataset, log_freq=50):
"""
Trains model on `dataset` using `optimizer`.
"""
# Metrics are stateful. They accumulate values and return a cumulative
# result when you call .result(). Clear accumulated values with .reset_states()
avg_loss = metrics.Mean('loss', dtype=tf.float32) #定义指标loss计算的规则:求loss平均值
# Datasets can be iterated over like any other Python iterable.
# 通过生成器每次遍历一个批量大小的数据
for images, labels in dataset:
loss = train_step(model, optimizer, images, labels) #计算这个批量大小的数据loss
avg_loss(loss) #计算loss的平均值
if tf.equal(optimizer.iterations % log_freq, 0):
# summary_ops_v2.scalar('loss', avg_loss.result(), step=optimizer.iterations)
# summary_ops_v2.scalar('accuracy', compute_accuracy.result(), step=optimizer.iterations)
print('step:', int(optimizer.iterations),
'loss:', avg_loss.result().numpy(),
'acc:', compute_accuracy.result().numpy())
avg_loss.reset_states() #清空
compute_accuracy.reset_states()
def test(model, dataset, step_num):
"""
Perform an evaluation of `model` on the examples from `dataset`.
"""
avg_loss = metrics.Mean('loss', dtype=tf.float32) #定义指标loss计算的规则:求loss平均值
for (images, labels) in dataset:
logits = model(images, training=False) #输入数据到模型中训练,预测输出logits标签
#compute_loss根据预测输出logits标签和真实标签labels,计算loss两者之间的误差值
avg_loss(compute_loss(labels, logits))#计算有loss的平均值
compute_accuracy(labels, logits) #根据预测输出logits标签和真实标签labels,计算accuracy两者之间的准确率
print('Model test set loss: {:0.4f} accuracy: {:0.2f}%'.format(avg_loss.result(), compute_accuracy.result() * 100))
print('loss:', avg_loss.result(), 'acc:', compute_accuracy.result())
# summary_ops_v2.scalar('loss', avg_loss.result(), step=step_num)
# summary_ops_v2.scalar('accuracy', compute_accuracy.result(), step=step_num)
# Where to save checkpoints, tensorboard summaries, etc.
MODEL_DIR = '/tmp/tensorflow/mnist'
def apply_clean():
if tf.io.gfile.exists(MODEL_DIR):
print('Removing existing model dir: {}'.format(MODEL_DIR))
tf.io.gfile.rmtree(MODEL_DIR)
apply_clean()
checkpoint_dir = os.path.join(MODEL_DIR, 'checkpoints')
checkpoint_prefix = os.path.join(checkpoint_dir, 'ckpt')
checkpoint = tf.train.Checkpoint(model=model, optimizer=optimizer)
# Restore variables on creation if a checkpoint exists.
checkpoint.restore(tf.train.latest_checkpoint(checkpoint_dir))
NUM_TRAIN_EPOCHS = 5
for i in range(NUM_TRAIN_EPOCHS):
start = time.time()
# with train_summary_writer.as_default():
train(model, optimizer, train_ds, log_freq=500)
end = time.time()
print('Train time for epoch #{} ({} total steps): {}'.format(
i + 1, int(optimizer.iterations), end - start))
# with test_summary_writer.as_default():
# test(model, test_ds, optimizer.iterations)
checkpoint.save(checkpoint_prefix)
print('saved checkpoint.')
export_path = os.path.join(MODEL_DIR, 'export')
tf.saved_model.save(model, export_path)
print('saved SavedModel for exporting.')
fc_train.py
import os
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers, optimizers, datasets
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # or any {'0', '1', '2'}
def mnist_dataset():
(x, y), _ = datasets.mnist.load_data()
ds = tf.data.Dataset.from_tensor_slices((x, y))#构建训练集:样品数据+真实标签
ds = ds.map(prepare_mnist_features_and_labels) #调用自定义函数对训练集数据进行标准化等预处理操作
ds = ds.take(20000).shuffle(20000).batch(100) #take取20000个训练样本+真实标签,然后shuffle打乱顺序,然后构建批量大小
return ds
@tf.function
def prepare_mnist_features_and_labels(x, y):
x = tf.cast(x, tf.float32) / 255.0 #训练样本数据标准化
y = tf.cast(y, tf.int64)
return x, y
model = keras.Sequential([
layers.Reshape(target_shape=(28 * 28,), input_shape=(28, 28)),
layers.Dense(100, activation='relu'),
layers.Dense(100, activation='relu'),
layers.Dense(10)])
optimizer = optimizers.Adam() #Adam优化算法
@tf.function
def compute_loss(logits, labels):
#定义并计算loss平均值
return tf.reduce_mean(
tf.nn.sparse_softmax_cross_entropy_with_logits(
logits=logits, labels=labels))
@tf.function
def compute_accuracy(logits, labels):
#获取每个样品的预测最大类别概率值的索引值,代表该类别的索引值
predictions = tf.argmax(logits, axis=1)
#比较预测最大类别的索引值和真实类别值,返回bool值然后转换为数值,然后统计平均值
return tf.reduce_mean(tf.cast(tf.equal(predictions, labels), tf.float32))
@tf.function
def train_one_step(model, optimizer, x, y):
#构建梯度记录环境
with tf.GradientTape() as tape:
logits = model(x) #输入数据到模型中训练,预测输出logits标签
loss = compute_loss(logits, y) #根据预测输出logits标签和真实标签labels,计算loss两者之间的误差值
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
# compute gradient
grads = tape.gradient(loss, model.trainable_variables)
#优化器规则,根据 模型参数θ = θ - lr * grad 更新网络参数
# update to weights
optimizer.apply_gradients(zip(grads, model.trainable_variables))
#根据预测输出logits标签和真实标签labels,计算accuracy两者之间的准确率
accuracy = compute_accuracy(logits, y)
# loss and accuracy is scalar tensor
return loss, accuracy
def train(epoch, model, optimizer):
train_ds = mnist_dataset()
loss = 0.0
accuracy = 0.0
# 通过生成器每次遍历一个批量大小的数据
for step, (x, y) in enumerate(train_ds):
loss, accuracy = train_one_step(model, optimizer, x, y)
if step % 500 == 0:
print('epoch', epoch, ': loss', loss.numpy(), '; accuracy', accuracy.numpy())
return loss, accuracy
for epoch in range(20):
loss, accuracy = train(epoch, model, optimizer)
print('Final epoch', epoch, ': loss', loss.numpy(), '; accuracy', accuracy.numpy())
AutoGraph
import tensorflow as tf
import timeit
cell = tf.keras.layers.LSTMCell(10)
@tf.function
def fn(input, state):
"""
use static graph to compute LSTM
:param input:
:param state:
:return:
"""
return cell(input, state)
input = tf.zeros([10, 10])
state = [tf.zeros([10, 10])] * 2
# warmup
cell(input, state) #动态图计算
fn(input, state) #静态图计算
dynamic_graph_time = timeit.timeit(lambda: cell(input, state), number=100) #动态图计算100次耗时
static_graph_time = timeit.timeit(lambda: fn(input, state), number=100) #静态图计算100次耗时
print('dynamic_graph_time:', dynamic_graph_time) #0.05584586199999997
print('static_graph_time:', static_graph_time) #0.02275101700000004
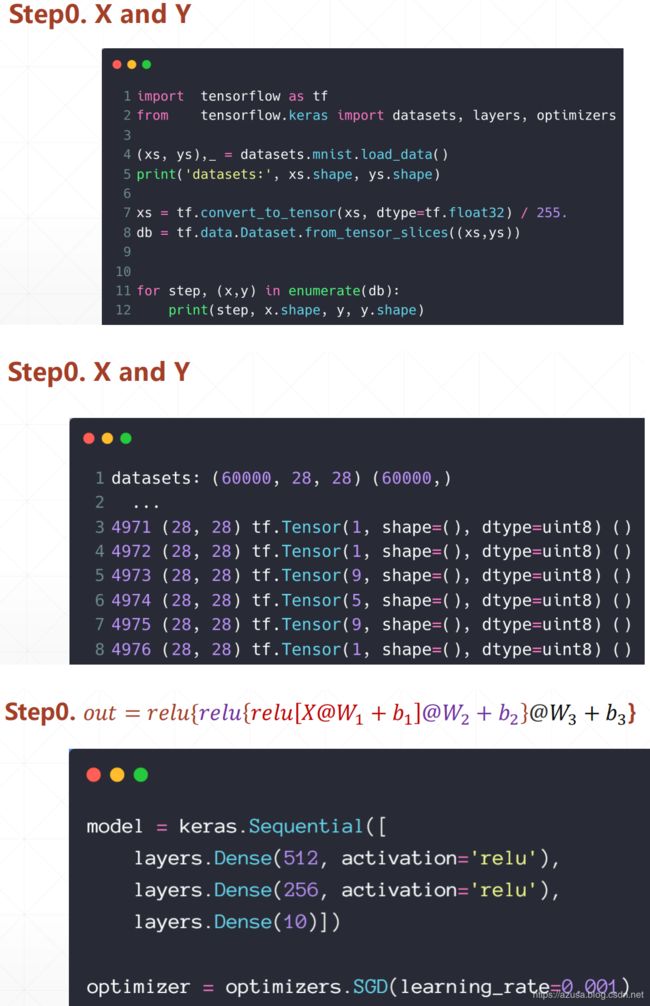
Play with MNIST
import tensorflow as tf
from tensorflow.keras import datasets, layers, optimizers, Sequential, metrics
(xs, ys),_ = datasets.mnist.load_data()
print('datasets:', xs.shape, ys.shape, xs.min(), xs.max())
xs = tf.convert_to_tensor(xs, dtype=tf.float32) / 255. #标准化/归一化
db = tf.data.Dataset.from_tensor_slices((xs,ys)) #构建样本集数据+标签集数据
db = db.batch(32).repeat(10) #batch构建批量大小、repeat定义epoch训练次数
network = Sequential([layers.Dense(256, activation='relu'),
layers.Dense(256, activation='relu'),
layers.Dense(256, activation='relu'),
layers.Dense(10)])
network.build(input_shape=(None, 28*28))
network.summary()
optimizer = optimizers.SGD(lr=0.01) #SGD随机梯度下降
acc_meter = metrics.Accuracy() #定义准确率指标Accuracy
for step, (x,y) in enumerate(db):
#构建梯度记录环境
with tf.GradientTape() as tape:
# [b, 28, 28] => [b, 784]
x = tf.reshape(x, (-1, 28*28))
# [b, 784] => [b, 10] 输出模型预测值
out = network(x)
# [b] => [b, 10] 真实标签one-hot化
y_onehot = tf.one_hot(y, depth=10)
#均方差mse = mean(sum(y-out)^2) 预测值与真实值之差的平方的平均值
# [b, 10] 计算每个样本的平均误差
loss = tf.square(out-y_onehot)
# [b] 把总误差除以总样本数
loss = tf.reduce_sum(loss) / 32
acc_meter.update_state(tf.argmax(out, axis=1), y) #把预测最大概率的类别索引值和真实标签传入准确率指标Accuracy中进行计算准确率结果
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
grads = tape.gradient(loss, network.trainable_variables)
#优化器规则,根据 模型参数θ = θ - lr * grad 更新网络参数
optimizer.apply_gradients(zip(grads, network.trainable_variables))
if step % 200==0:
print(step, 'loss:', float(loss), 'acc:', acc_meter.result().numpy())
acc_meter.reset_states()
mnist_tensor.py
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets, layers, optimizers
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
print(tf.__version__)
def preprocess(x, y):
# [b, 28, 28], [b]
x = tf.cast(x, dtype=tf.float32) / 255. #标准化/归一化
x = tf.reshape(x, [-1, 28*28]) #展平为(批量大小,行*列)
y = tf.cast(y, dtype=tf.int32)
y = tf.one_hot(y, depth=10) #真实标签one-hot化
return x,y
(x, y), (x_test, y_test) = datasets.mnist.load_data()
print('x:', x.shape, 'y:', y.shape, 'x test:', x_test.shape, 'y test:', y_test)
train_db = tf.data.Dataset.from_tensor_slices((x, y))
#shuffle打乱样本顺序,batch构建批量大小,map对数据执行preprocess函数实现的数据标准化,repeat定义epoch训练次数
train_db = train_db.shuffle(60000).batch(128).map(preprocess).repeat(30)
test_db = tf.data.Dataset.from_tensor_slices((x_test, y_test))
#shuffle打乱样本顺序,batch构建批量大小,map对数据执行preprocess函数实现的数据标准化
test_db = test_db.shuffle(10000).batch(128).map(preprocess)
x,y = next(iter(train_db)) #iter返回生成器对象,next调用生成器返回第一个批量大小的数据
print('train sample:', x.shape, y.shape)
# print(x[0], y[0])
def main():
# learning rate 学习率
lr = 1e-3
# 784 => 512 [dim_in, dim_out], [dim_out] 第一层权重[输入神经元节点数, 输出神经元节点数]、偏置[输出神经元节点数]
w1, b1 = tf.Variable(tf.random.truncated_normal([784, 512], stddev=0.1)), tf.Variable(tf.zeros([512]))
# 512 => 256
w2, b2 = tf.Variable(tf.random.truncated_normal([512, 256], stddev=0.1)), tf.Variable(tf.zeros([256]))
# 256 => 10
w3, b3 = tf.Variable(tf.random.truncated_normal([256, 10], stddev=0.1)), tf.Variable(tf.zeros([10]))
#遍历生成器对象,每次获取每个批量大小的数据
for step, (x,y) in enumerate(train_db):
# [b, 28, 28] => [b, 784] 展平为 (批量大小,行*列)
x = tf.reshape(x, (-1, 784))
#构建梯度记录环境
with tf.GradientTape() as tape:
# layer1.
h1 = x @ w1 + b1
h1 = tf.nn.relu(h1)
# layer2
h2 = h1 @ w2 + b2
h2 = tf.nn.relu(h2)
# output
out = h2 @ w3 + b3
# out = tf.nn.relu(out)
# compute loss 均方差mse = mean(sum(y-out)^2) 预测值与真实值之差的平方的平均值
# [b, 10] - [b, 10]
loss = tf.square(y-out)
# [b, 10] => [b] 计算每个样本的平均误差
loss = tf.reduce_mean(loss, axis=1)
# [b] => scalar 计算总的平均误差
loss = tf.reduce_mean(loss)
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
# compute gradient
grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# for g in grads:
# print(tf.norm(g))
# update w' = w - lr*grad
for p, g in zip([w1, b1, w2, b2, w3, b3], grads):
#优化器规则,根据 模型参数θ = θ - lr * grad 更新网络参数
p.assign_sub(lr * g)
# print
if step % 100 == 0:
print(step, 'loss:', float(loss))
# evaluate
if step % 500 == 0:
total, total_correct = 0., 0
#遍历测试集的生成器,获取每个批量大小的数据进行验证
for step, (x, y) in enumerate(test_db):
# layer1.
h1 = x @ w1 + b1
h1 = tf.nn.relu(h1)
# layer2
h2 = h1 @ w2 + b2
h2 = tf.nn.relu(h2)
# output
out = h2 @ w3 + b3
# [b, 10] => [b]
pred = tf.argmax(out, axis=1)
# convert one_hot y to number y
y = tf.argmax(y, axis=1)
# bool type
correct = tf.equal(pred, y)
# bool tensor => int tensor => numpy
total_correct += tf.reduce_sum(tf.cast(correct, dtype=tf.int32)).numpy()
total += x.shape[0]
print(step, 'Evaluate Acc:', total_correct/total)
if __name__ == '__main__':
main()
forward.py
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# x: [60k, 28, 28], [10, 28, 28]
# y: [60k], [10k]
(x, y), (x_test, y_test) = datasets.mnist.load_data()
# x: [0~255] => [0~1.]
x = tf.convert_to_tensor(x, dtype=tf.float32) / 255. #标准化/归一化
y = tf.convert_to_tensor(y, dtype=tf.int32)
x_test = tf.convert_to_tensor(x_test, dtype=tf.float32) / 255. #标准化/归一化
y_test = tf.convert_to_tensor(y_test, dtype=tf.int32)
print(x.shape, y.shape, x.dtype, y.dtype)
print(tf.reduce_min(x), tf.reduce_max(x))
print(tf.reduce_min(y), tf.reduce_max(y))
#batch构建批量大小
train_db = tf.data.Dataset.from_tensor_slices((x,y)).batch(128)
test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test)).batch(128)
train_iter = iter(train_db) #iter返回生成器对象
sample = next(train_iter) #next调用生成器返回第一个批量大小的数据
print('batch:', sample[0].shape, sample[1].shape)
# [b, 784] => [b, 256] => [b, 128] => [b, 10]
# [dim_in, dim_out], [dim_out] 第一层权重[输入神经元节点数, 输出神经元节点数]、偏置[输出神经元节点数]
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1))
b2 = tf.Variable(tf.zeros([128]))
w3 = tf.Variable(tf.random.truncated_normal([128, 10], stddev=0.1))
b3 = tf.Variable(tf.zeros([10]))
lr = 1e-3 #学习率
#构建epoch训练次数
for epoch in range(100): # iterate db for 10
#遍历生成器对象,每次获取每个批量大小的数据
for step, (x, y) in enumerate(train_db): # for every batch
# x:[128, 28, 28]
# y: [128]
# [b, 28, 28] => [b, 28*28] 展平为 (批量大小,行*列)
x = tf.reshape(x, [-1, 28*28])
#构建梯度记录环境
with tf.GradientTape() as tape: # tf.Variable
# x: [b, 28*28]
# h1 = x@w1 + b1
# [b, 784]@[784, 256] + [256] => [b, 256] + [256] => [b, 256] + [b, 256]
h1 = x@w1 + tf.broadcast_to(b1, [x.shape[0], 256])
h1 = tf.nn.relu(h1)
# [b, 256] => [b, 128]
h2 = h1@w2 + b2
h2 = tf.nn.relu(h2)
# [b, 128] => [b, 10]
out = h2@w3 + b3
# compute loss
# out: [b, 10]
# y: [b] => [b, 10] 真实标签one-hot化
y_onehot = tf.one_hot(y, depth=10)
# mse = mean(sum(y-out)^2)
# [b, 10] 均方差mse = mean(sum(y-out)^2) 预测值与真实值之差的平方的平均值
loss = tf.square(y_onehot - out)
# mean: scalar
loss = tf.reduce_mean(loss)
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
# compute gradients
grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# print(grads)
# w1 = w1 - lr * w1_grad 优化器规则,根据 模型参数θ = θ - lr * grad 更新网络参数
w1.assign_sub(lr * grads[0])
b1.assign_sub(lr * grads[1])
w2.assign_sub(lr * grads[2])
b2.assign_sub(lr * grads[3])
w3.assign_sub(lr * grads[4])
b3.assign_sub(lr * grads[5])
if step % 100 == 0:
print(epoch, step, 'loss:', float(loss))
# test/evluation
# [w1, b1, w2, b2, w3, b3]
total_correct, total_num = 0, 0
for step, (x,y) in enumerate(test_db):
# [b, 28, 28] => [b, 28*28]
x = tf.reshape(x, [-1, 28*28])
# [b, 784] => [b, 256] => [b, 128] => [b, 10]
h1 = tf.nn.relu(x@w1 + b1)
h2 = tf.nn.relu(h1@w2 + b2)
out = h2@w3 +b3
# out: [b, 10] ~ R
# prob: [b, 10] ~ [0, 1]
prob = tf.nn.softmax(out, axis=1)
# [b, 10] => [b]
# int64!!!
pred = tf.argmax(prob, axis=1)
pred = tf.cast(pred, dtype=tf.int32)
# y: [b]
# [b], int32
# print(pred.dtype, y.dtype)
correct = tf.cast(tf.equal(pred, y), dtype=tf.int32)
correct = tf.reduce_sum(correct)
total_correct += int(correct)
total_num += x.shape[0]
acc = total_correct / total_num
print('test acc:', acc)
回归问题、分类问题
自动求梯度
import tensorflow as tf
# 创建 4 个张量
a = tf.constant(1.)
b = tf.constant(2.)
c = tf.constant(3.)
w = tf.constant(4.)
# 构建梯度环境
with tf.GradientTape() as tape:
# 将 w 加入梯度跟踪列表
tape.watch([w])
# 构建计算过程
y = a * w**2 + b * w + c
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 求导
[dy_dw] = tape.gradient(y, [w])
print(dy_dw) # 打印出导数 tf.Tensor(10.0, shape=(), dtype=float32)
import tensorflow as tf
# 创建4个张量
a = tf.constant(1.)
b = tf.constant(2.)
c = tf.constant(3.)
w = tf.constant(4.)
with tf.GradientTape() as tape:# 构建梯度环境
tape.watch([w]) # 将w加入梯度跟踪列表
# 构建计算过程
y = a * w**2 + b * w + c
# 求导
[dy_dw] = tape.gradient(y, [w])
print(dy_dw)
手动求梯度
均方差MSE
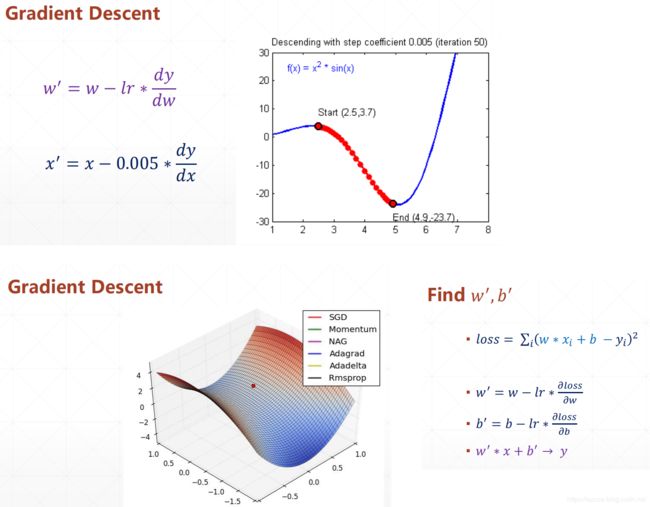
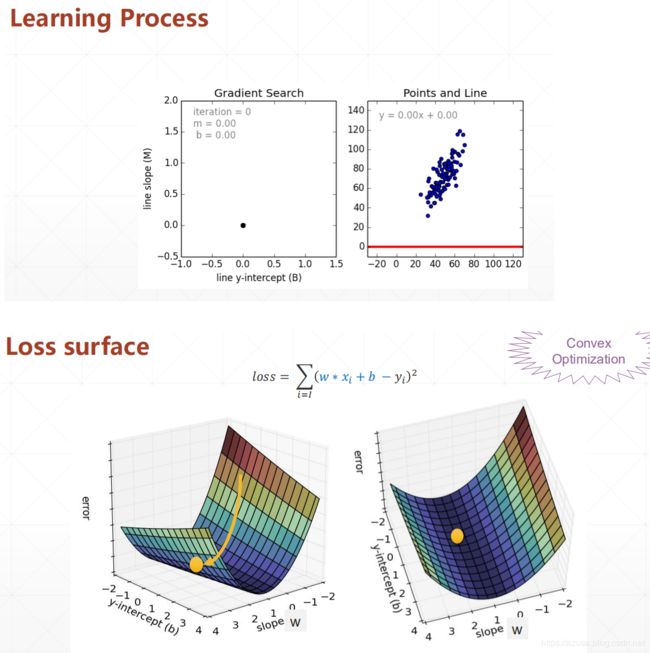
函数求导、梯度下降、导数和偏导数
线性模型的求导、梯度下降
import numpy as np
# data = []
# for i in range(100):
# x = np.random.uniform(3., 12.)
# # mean=0, std=0.1
# eps = np.random.normal(0., 0.1)
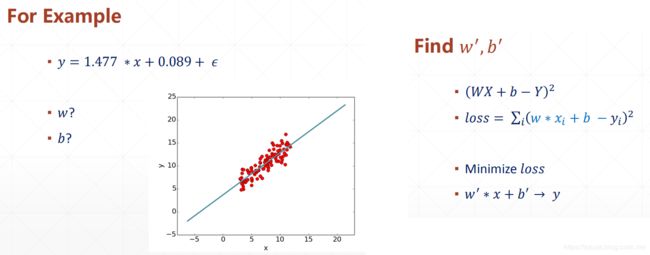
# y = 1.477 * x + 0.089 + eps
# data.append([x, y])
# data = np.array(data)
# print(data.shape, data)
# y = wx + b
def compute_error_for_line_given_points(b, w, points):
totalError = 0
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
# computer mean-squared-error
totalError += (y - (w * x + b)) ** 2
# average loss for each point
return totalError / float(len(points))
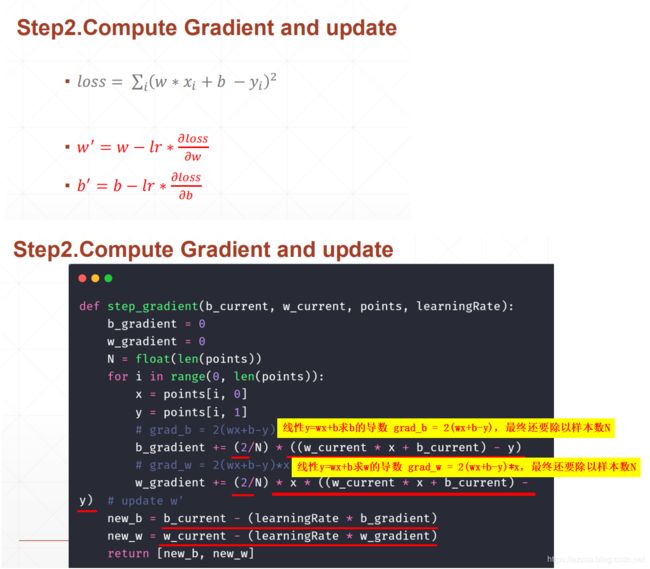
def step_gradient(b_current, w_current, points, learningRate):
b_gradient = 0
w_gradient = 0
N = float(len(points))
for i in range(0, len(points)):
x = points[i, 0]
y = points[i, 1]
# grad_b = 2(wx+b-y)
b_gradient += (2/N) * ((w_current * x + b_current) - y)
# grad_w = 2(wx+b-y)*x
w_gradient += (2/N) * x * ((w_current * x + b_current) - y)
# update w'
new_b = b_current - (learningRate * b_gradient)
new_w = w_current - (learningRate * w_gradient)
return [new_b, new_w]
def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
b = starting_b
w = starting_w
# update for several times
for i in range(num_iterations):
b, w = step_gradient(b, w, np.array(points), learning_rate)
return [b, w]
def run():
points = np.genfromtxt("data.csv", delimiter=",")
learning_rate = 0.0001
initial_b = 0 # initial y-intercept guess
initial_w = 0 # initial slope guess
num_iterations = 1000
print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
.format(initial_b, initial_w,
compute_error_for_line_given_points(initial_b, initial_w, points))
)
print("Running...")
[b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
print("After {0} iterations b = {1}, w = {2}, error = {3}".
format(num_iterations, b, w,
compute_error_for_line_given_points(b, w, points))
)
if __name__ == '__main__':
run()
import tensorflow as tf
import numpy as np
from tensorflow import keras
import os
class Regressor(keras.layers.Layer):
def __init__(self):
super(Regressor, self).__init__()
# here must specify shape instead of tensor !
# name here is meanless !
# [dim_in, dim_out] 即[输入维度,输出维度]
self.w = self.add_variable('meanless-name', [13, 1])
# [dim_out] 即[输出维度]
self.b = self.add_variable('meanless-name', [1])
print(self.w.shape, self.b.shape)
print(type(self.w), tf.is_tensor(self.w), self.w.name)
print(type(self.b), tf.is_tensor(self.b), self.b.name)
def call(self, x):
#即线性w@x+b
x = tf.matmul(x, self.w) + self.b
return x
def main():
tf.random.set_seed(22)
np.random.seed(22)
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
assert tf.__version__.startswith('2.')
#加载波士顿房屋数据
(x_train, y_train), (x_val, y_val) = keras.datasets.boston_housing.load_data()
x_train, x_val = x_train.astype(np.float32), x_val.astype(np.float32)
# (404, 13) (404,) (102, 13) (102,)
print(x_train.shape, y_train.shape, x_val.shape, y_val.shape)
# Here has two mis-leading issues:
# 1.(x_train, y_train) cant be written as [x_train, y_train]
# 2.(x_val, y_val) cant be written as [x_val, y_val]
db_train = tf.data.Dataset.from_tensor_slices((x_train, y_train)).batch(64) #构建批量大小为64的样本特征数据集+真实标签数据集
db_val = tf.data.Dataset.from_tensor_slices((x_val, y_val)).batch(102) #构建批量大小为102的样本特征数据集+真实标签数据集
model = Regressor() #定义模型类对象
criteon = keras.losses.MeanSquaredError() #定义均方差mse = mean(sum(y-out)^2) 预测值与真实值之差的平方的平均值
optimizer = keras.optimizers.Adam(learning_rate=1e-2) #Adam优化算法
#定义epoch训练次数
for epoch in range(200):
#每次遍历数据集的一个批量大小的数据
for step, (x, y) in enumerate(db_train):
#构建梯度记录环境
with tf.GradientTape() as tape:
# [b, 1] 输出预测值
logits = model(x)
# [b] squeeze降维/压缩维度,把axis=1即维度为1的第二维度删除掉
logits = tf.squeeze(logits, axis=1)
# [b] vs [b] 传入预测值logits和真实标签y计算loss
loss = criteon(y, logits)
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
grads = tape.gradient(loss, model.trainable_variables)
#优化器规则,根据 模型参数θ = θ - lr * grad 更新网络参数
optimizer.apply_gradients(zip(grads, model.trainable_variables))
print(epoch, 'loss:', loss.numpy())
if epoch % 10 == 0:
for x, y in db_val:
# [b, 1]
logits = model(x)
# [b]
logits = tf.squeeze(logits, axis=1)
# [b] vs [b]
loss = criteon(y, logits)
print(epoch, 'val loss:', loss.numpy())
if __name__ == '__main__':
main()
分类问题
import tensorflow as tf
from tensorflow.keras import datasets, layers, optimizers, Sequential, metrics
# 设置GPU使用方式
# 获取GPU列表
gpus = tf.config.experimental.list_physical_devices('GPU')
if gpus:
try:
# 设置GPU为增长式占用
for gpu in gpus:
tf.config.experimental.set_memory_growth(gpu, True)
except RuntimeError as e:
# 打印异常
print(e)
#获取训练集数据和标签集
(xs, ys),_ = datasets.mnist.load_data()
#datasets: (60000, 28, 28) (60000,) 0 255
print('datasets:', xs.shape, ys.shape, xs.min(), xs.max())
#批量大小(样本数)
batch_size = 32
#归一化/标准化
xs = tf.convert_to_tensor(xs, dtype=tf.float32) / 255.
#构建
db = tf.data.Dataset.from_tensor_slices((xs,ys))
print(db) #
#batch()构建批量大小、repeat(30) 数据集遍历 30遍才终止
db = db.batch(batch_size).repeat(30)
print(db) #
model = Sequential([layers.Dense(256, activation='relu'),
layers.Dense(128, activation='relu'),
layers.Dense(10)])
model.build(input_shape=(4, 28*28))
model.summary()
#随机梯度下降SGD
optimizer = optimizers.SGD(lr=0.01)
#准确率
acc_meter = metrics.Accuracy()
#每次遍历数据集中的批量大小的数据
for step, (x,y) in enumerate(db):
#构建梯度记录环境
with tf.GradientTape() as tape:
# 打平操作,[b, 28, 28] => [b, 784]
x = tf.reshape(x, (-1, 28*28))
# Step1. 得到模型输出output [b, 784] => [b, 10]
out = model(x)
# [b] => [b, 10]
y_onehot = tf.one_hot(y, depth=10)
# 计算差的平方和,[b, 10]
loss = tf.square(out-y_onehot)
# 计算每个样本的平均误差,[b]。总误差除以样本数x.shape[0]
loss = tf.reduce_sum(loss) / x.shape[0]
#根据预测值tf.argmax(out, axis=1)与真实值y写入测量器,计算准确率
acc_meter.update_state(tf.argmax(out, axis=1), y)
#求导,根据loss对模型所有参数求导
grads = tape.gradient(loss, model.trainable_variables)
#优化器规则,根据 模型参数θ = θ - lr * grad 更新网络参数
optimizer.apply_gradients(zip(grads, model.trainable_variables))
if step % 200==0:
print(step, 'loss:', float(loss), 'acc:', acc_meter.result().numpy()) #读取统计结果
acc_meter.reset_states() #清零测量器
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers, optimizers, datasets
(x, y), (x_val, y_val) = datasets.mnist.load_data()
#训练集图像标准化
x = tf.convert_to_tensor(x, dtype=tf.float32) / 255.
#把标签数据转换为矩阵
y = tf.convert_to_tensor(y, dtype=tf.int32)
#把每个标签one-hot化,每个标签的维度是10,目的是把本身为连续值的标签值向量化之后,以便于训练,因为连续值本身无法用于直接学习
y = tf.one_hot(y, depth=10)
print(x.shape, y.shape)
#构建训练集和标签集数据用于训练
train_dataset = tf.data.Dataset.from_tensor_slices((x, y))
#构建批量大小
train_dataset = train_dataset.batch(200)
#三层模型:前两次层都是线性+非线性relu的组合,第三层直接是线性
model = keras.Sequential([
layers.Dense(512, activation='relu'),
layers.Dense(256, activation='relu'),
layers.Dense(10)])
#SGD随机梯度下降的优化器
optimizer = optimizers.SGD(learning_rate=0.001)
def train_epoch(epoch):
# Step4.loop 每次遍历数据集中的批量大小的数据
for step, (x, y) in enumerate(train_dataset):
#构建梯度记录环境
with tf.GradientTape() as tape:
# 展平化为(批量大小,行*列) [b, 28, 28] => [b, 784]
x = tf.reshape(x, (-1, 28*28))
# Step1. compute output 从输入的784维转换为输出的10维
# [b, 784] => [b, 10]
out = model(x)
# Step2. compute loss 计算每个样本的平均误差,把总误差除以总样本数
loss = tf.reduce_sum(tf.square(out - y)) / x.shape[0]
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# 根据loss对模型所有参数求导 tape.gradient(loss, model.trainable_variables)
# Step3. optimize and update w1, w2, w3, b1, b2, b3
# 根据loss 求w1, w2, w3, b1, b2, b3的梯度值 用于后面继续更新对应的模型参数θ
grads = tape.gradient(loss, model.trainable_variables)
# w' = w - lr * grad
#优化器规则,根据 模型参数θ = θ - lr * grad 更新网络参数
optimizer.apply_gradients(zip(grads, model.trainable_variables))
if step % 100 == 0:
print(epoch, step, 'loss:', loss.numpy())
def train():
for epoch in range(30):
train_epoch(epoch)
if __name__ == '__main__':
train()
import matplotlib
from matplotlib import pyplot as plt
# Default parameters for plots
matplotlib.rcParams['font.size'] = 20
matplotlib.rcParams['figure.titlesize'] = 20
matplotlib.rcParams['figure.figsize'] = [9, 7]
matplotlib.rcParams['font.family'] = ['STKaiTi']
matplotlib.rcParams['axes.unicode_minus']=False
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# x: [60k, 28, 28] (样本数,行,列)
# y: [60k] (样本数)
(x, y), _ = datasets.mnist.load_data()
# x: [0~255] => [0~1.] 把像素点标准化
x = tf.convert_to_tensor(x, dtype=tf.float32) / 255.
y = tf.convert_to_tensor(y, dtype=tf.int32)
print(x.shape, y.shape, x.dtype, y.dtype) #(60000, 28, 28) (60000,)
print(tf.reduce_min(x), tf.reduce_max(x)) #tf.Tensor(0.0, shape=(), dtype=float32) tf.Tensor(1.0, shape=(), dtype=float32)
print(tf.reduce_min(y), tf.reduce_max(y)) #tf.Tensor(0, shape=(), dtype=int32) tf.Tensor(9, shape=(), dtype=int32)
#构建批量大小
train_db = tf.data.Dataset.from_tensor_slices((x,y)).batch(128)
train_iter = iter(train_db) #把训练集构建为迭代器
sample = next(train_iter) #每次next均为获取下一个128批量大小的样本数据+标签数据
print('batch:', sample[0].shape, sample[1].shape) #batch: (128, 28, 28) (128,)
# [b, 784] => [b, 256] => [b, 128] => [b, 10]。b为批量大小,784为输入层维度,256和128均为隐藏层的神经数量,10为输出层的神经元数量。
# [dim_in, dim_out], [dim_out]
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1)) #第一层权重矩阵的维度
b1 = tf.Variable(tf.zeros([256])) #第一层偏置向量的维度
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1)) #第二层权重矩阵的维度
b2 = tf.Variable(tf.zeros([128])) #第二层偏置向量的维度
w3 = tf.Variable(tf.random.truncated_normal([128, 10], stddev=0.1)) #第三层权重矩阵的维度
b3 = tf.Variable(tf.zeros([10])) #第三层偏置向量的维度
lr = 1e-3 #学习率
losses = []
for epoch in range(20): # iterate db for 10
# 每次遍历数据集中的批量大小的数据
for step, (x, y) in enumerate(train_db): # for every batch
# x:[128, 28, 28]。y: [128]。
# 展平化 (批量大小,行*列) [b, 28, 28] => [b, 28*28]
x = tf.reshape(x, [-1, 28*28])
#构建梯度记录环境
with tf.GradientTape() as tape: # tf.Variable
# 输入x的维度: [b, 28*28]。b为批量大小。
# 计算第一层线性输出 h1 = x@w1 + b1(X@W表示矩阵乘法运算)
# 第一层线性输出的维度计算转换流程 [b, 784]@[784, 256] + [256] => [b, 256] + [256] => [b, 256] + [b, 256] => [b, 256]
# tf.broadcast_to(b1, [x.shape[0], 256]) 表示把 [256]维度的偏置 广播为 [b, 256] 的维度大小
h1 = x@w1 + tf.broadcast_to(b1, [x.shape[0], 256])
# 计算第一层非线性输出relu
h1 = tf.nn.relu(h1)
# 第二层线性输出的维度计算转换流程 [b, 256]@[256, 128] + [128] => [b, 128] + [128]=> [b, 128]
h2 = h1@w2 + b2
# 计算第二层非线性输出relu
h2 = tf.nn.relu(h2)
# 输出层输出的维度计算流程 [b, 128]@[128, 10] + [10] => [b, 10] + [10] => [b, 10]
out = h2@w3 + b3
# compute loss
# out: [b, 10]
# 真实标签值y 进行one-hot向量化,维度为10: [b] => [b, 10]
y_onehot = tf.one_hot(y, depth=10)
# 均方差mse = mean(sum(y-out)^2) 预测值与真实值之差的平方的平均值
# [b, 10]
loss = tf.square(y_onehot - out) # 计算每个样本的 MSE
# mean: scalar
loss = tf.reduce_mean(loss) #平均 MSE,计算平均值
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# compute gradients。根据loss 求w1, w2, w3, b1, b2, b3的梯度值 用于后面继续更新对应的模型参数θ。
grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# print(grads)
#根据 模型参数θ = θ - lr * grad 更新网络参数
w1.assign_sub(lr * grads[0]) # w1 = w1 - lr * w1_grad
b1.assign_sub(lr * grads[1]) # b1 = b1 - lr * b1_grad
w2.assign_sub(lr * grads[2]) # w2 = w2 - lr * w2_grad
b2.assign_sub(lr * grads[3]) # b2 = b2 - lr * b2_grad
w3.assign_sub(lr * grads[4]) # w3 = w3 - lr * w3_grad
b3.assign_sub(lr * grads[5]) # b3 = b3 - lr * b3_grad
if step % 100 == 0:
print(epoch, step, 'loss:', float(loss))
losses.append(float(loss))
plt.figure()
plt.plot(losses, color='C0', marker='s', label='шонч╗Г')
plt.xlabel('Epoch')
plt.legend()
plt.ylabel('MSE')
plt.savefig('forward.svg')
# plt.show()
import numpy as np
# y = wx + b
def compute_error_for_line_given_points(b, w, points):
totalError = 0
for i in range(0, len(points)):#遍历次数 0~样本数
x = points[i, 0] #该行样本数据的特征值
y = points[i, 1] #该行样本数据对应的真实标签值
# computer mean-squared-error 均方差mse = mean(sum(y-out)^2) 预测值与真实值之差的平方的平均值
totalError += (y - (w * x + b)) ** 2
# average loss for each point 总误差除以样本数
return totalError / float(len(points))
def step_gradient(b_current, w_current, points, learningRate):
b_gradient = 0 #线性y=wx+b求b的梯度值
w_gradient = 0 #线性y=wx+b求w的梯度值
N = float(len(points)) #样本数
for i in range(0, len(points)):#遍历次数 0~样本数
x = points[i, 0] #该行样本数据的特征值
y = points[i, 1] #该行样本数据对应的真实标签值
# 线性y=wx+b求b的导数 grad_b = 2(wx+b-y),最终还要除以样本数N
b_gradient += (2/N) * ((w_current * x + b_current) - y)
# 线性y=wx+b求w的导数 grad_w = 2(wx+b-y)*x,最终还要除以样本数N
w_gradient += (2/N) * x * ((w_current * x + b_current) - y)
# update w'、b'。根据 模型参数θ = θ - lr * grad 更新网络参数
new_b = b_current - (learningRate * b_gradient)
new_w = w_current - (learningRate * w_gradient)
return [new_b, new_w]
def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
b = starting_b
w = starting_w
# update for several times
#num_iterations定义epoch训练次数
for i in range(num_iterations):
b, w = step_gradient(b, w, np.array(points), learning_rate)
return [b, w]
def run():
points = np.genfromtxt("data.csv", delimiter=",")
learning_rate = 0.0001 #学习率
initial_b = 0 # initial y-intercept guess
initial_w = 0 # initial slope guess
num_iterations = 1000 #训练次数
print("Starting gradient descent at b = {0}, w = {1}, error = {2}"
.format(initial_b, initial_w,
compute_error_for_line_given_points(initial_b, initial_w, points))
)
print("Running...")
[b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
print("After {0} iterations b = {1}, w = {2}, error = {3}".
format(num_iterations, b, w,
compute_error_for_line_given_points(b, w, points))
)
if __name__ == '__main__':
run()
回归问题
手写数字问题
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='2'
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers, optimizers, datasets
(x, y), (x_val, y_val) = datasets.mnist.load_data()
x = tf.convert_to_tensor(x, dtype=tf.float32) / 255. #标准化/归一化
y = tf.convert_to_tensor(y, dtype=tf.int32)
y = tf.one_hot(y, depth=10) #真实标签one-hot化
print(x.shape, y.shape)
train_dataset = tf.data.Dataset.from_tensor_slices((x, y))
train_dataset = train_dataset.batch(200) #构建批量大小
model = keras.Sequential([
layers.Dense(512, activation='relu'),
layers.Dense(256, activation='relu'),
layers.Dense(10)])
optimizer = optimizers.SGD(learning_rate=0.001) #SGD随机梯度下降
def train_epoch(epoch):
# Step4.loop 遍历数据集中的每个批量大小的数据
for step, (x, y) in enumerate(train_dataset):
#构建梯度记录环境
with tf.GradientTape() as tape:
# [b, 28, 28] => [b, 784]
x = tf.reshape(x, (-1, 28*28))
# Step1. compute output 输出预测值
# [b, 784] => [b, 10]
out = model(x)
# Step2. compute loss 均方差mse = mean(sum(y-out)^2) 预测值与真实值之差的平方的平均值
loss = tf.reduce_sum(tf.square(out - y)) / x.shape[0]
#1.求导,tape.gradient(y,[参数θ])求参数θ相对于y的梯度信息
# dy_dw = tape.gradient(y, [w])
#2.通过tape.gradient(loss,[参数θ])函数求得网络参数θ的梯度信息
# grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])
# Step3. optimize and update w1, w2, w3, b1, b2, b3
grads = tape.gradient(loss, model.trainable_variables)
# w' = w - lr * grad。根据 模型参数θ = θ - lr * grad 更新网络参数。
optimizer.apply_gradients(zip(grads, model.trainable_variables))
if step % 100 == 0:
print(epoch, step, 'loss:', loss.numpy())
def train():
for epoch in range(30): #epoch训练30次
train_epoch(epoch)
if __name__ == '__main__':
train()