卷积神经网络CNN、感受野、边缘检测、卷积层(零填充padding、步长、多通道卷积、多卷积核)、池化层Pooling、全连接层
 日萌社
日萌社
人工智能AI:Keras PyTorch MXNet TensorFlow PaddlePaddle 深度学习实战(不定时更新)
3.3 卷积神经网络(CNN)
3.3.1 为什么需要卷积神经网络
在计算机视觉领域,通常要做的就是指用机器程序替代人眼对目标图像进行识别等。那么神经网络也好还是卷积神经网络其实都是上个世纪就有的算法,只是近些年来电脑的计算能力已非当年的那种计算水平,同时现在的训练数据很多,于是神经网络的相关算法又重新流行起来,因此卷积神经网络也一样流行。
- 1974年,Paul Werbos提出了误差反向传导来训练人工神经网络,使得训练多层神经网络成为可能。
- 1979年,Kunihiko Fukushima(福岛邦彦),提出了Neocognitron, 卷积、池化的概念基本形成。
- 1986年,Geoffrey Hinton与人合著了一篇论文:Learning representations by back-propagation errors。
- 1989年,Yann LeCun提出了一种用反向传导进行更新的卷积神经网络,称为LeNet。
- 1998年,Yann LeCun改进了原来的卷积网络,LeNet-5。
3.1.1.2 图像特征数量对神经网络效果压力
假设下图是一图片大小为28 * 28 的黑白图片时候,每一个像素点只有一个值(单通道)。那么总的数值个数为 784个特征。
那现在这张图片是彩色的,那么彩色图片由RGB三通道组成,也就意味着总的数值有28 28 3 = 2352个值。
从上面我们得到一张图片的输入是2352个特征值,即神经网路当中与若干个神经元连接,假设第一个隐层是10个神经元,那么也就是23520个权重参数。
如果图片再大一些呢,假设图片为1000*1000*3,那么总共有3百万数值,同样接入10个神经元,那么就是3千万个权重参数。这样的参数大小,神经网络参数更新需要大量的计算不说,也很难达到更好的效果,大家就不倾向于使用多层神经网络了。
所以就有了卷积神经网络的流行,那么卷积神经网络为什么大家会选择它。那么先来介绍感受野以及边缘检测的概念。
3.3.2 感受野的来源
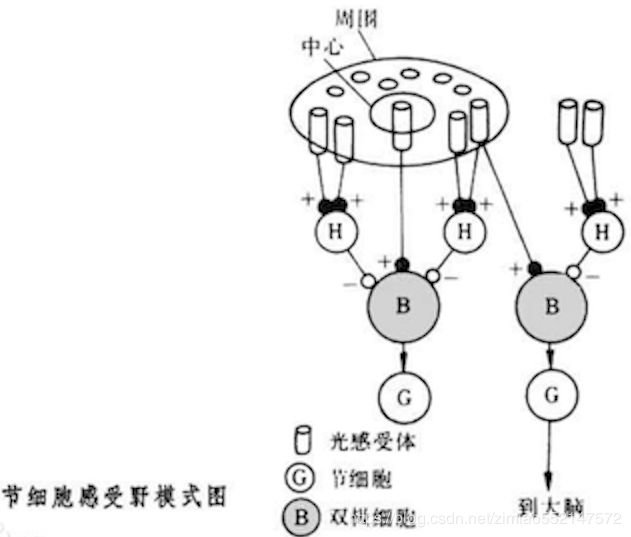
1962年Hubel和Wiesel通过对猫视觉皮层细胞的研究,提出了感受野(receptive field)的概念,Fukushima基于感受野概念提出的神经认知机(neocognitron)可以看作是卷积神经网络的第一个实现网络。
单个感受器与许多感觉神经纤维相联系,感觉信息是通过许多感受神经纤维得到神经冲动。一个神经元所反应的刺激区域就叫做神经元的感受野(receptive field)
在机器视觉领域的深度神经网络中有一个概念叫做感受野,用来表示网络内部的不同位置的神经元对原图像的感受范围的大小。
3.3.3 边缘检测
为了能够用更少的参数,检测出更多的信息,基于上面的感受野思想。通常神经网络需要检测出物体最明显的垂直和水平边缘来区分物体。比如
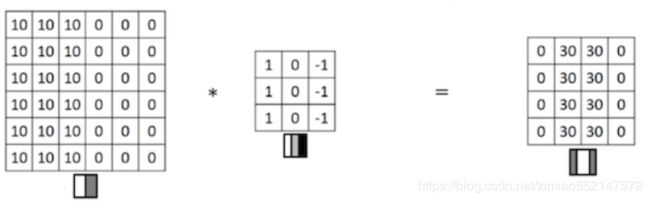
看一个列子,一个 6×6的图像卷积与一个3×3的过滤器(Filter or kenel)进行卷积运算(符号为 ), 也可能是矩阵乘法所以通常特别指定是卷积的时候代表卷积意思。
- 相当于将 Filter 放在Image 上,从左到右、从上到下地(默认一个像素)移动过整个Image,分别计算 ImageImage 被 Filter 盖住的部分与 Filter的逐元素乘积的和
在这个6×6 的图像中,左边一半像素的值全是 10,右边一半像素的值全是 0,中间是一条非常明显的垂直边缘。这个图像与过滤器卷积的结果中,中间两列的值都是 30,两边两列的值都是 0,即检测到了原 6×6 图像中的垂直边缘。
注:虽然看上去非常粗,是因为我们的图像太小,只有5个像素长、宽,所以最终得到结果看到的是两个像素位置,如果在一个500 x 500的图当中,就是一个竖直的边缘了。(通常正的表示亮,负的表示暗)
随着深度学习的发展,我们需要检测更复杂的图像中的边缘,与其使用由人手工设计的过滤器,还可以将过滤器中的数值作为参数,通过反向传播来学习得到。算法可以根据实际数据来选择合适的检测目标,无论是检测水平边缘、垂直边缘还是其他角度的边缘,并习得图像的低层特征。
3.3.4 卷积神经网络的组成
- 定义
- 卷积神经网络由一个或多个卷积层、池化层以及全连接层等组成。与其他深度学习结构相比,卷积神经网络在图像等方面能够给出更好的结果。这一模型也可以使用反向传播算法进行训练。相比较其他浅层或深度神经网络,卷积神经网络需要考量的参数更少,使之成为一种颇具吸引力的深度学习结构。
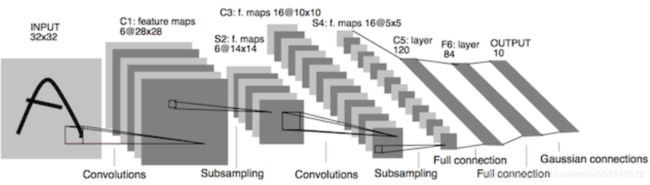
我们来看一下卷积网络的整体结构什么样子。
其中包含了几个主要结构
- 卷积层(Convolutions)
- 池化层(Subsampling)
- 全连接层(Full connection)
- 激活函数
3.3.4.1 卷积层
- 目的
- 卷积运算的目的是提取输入的不同特征,某些卷积层可能只能提取一些低级的特征如边缘、线条等层级,更多层的网路能从低级特征中迭代提取更复杂的特征。
- 参数:
- size:卷积核/过滤器大小,选择有1*1,3*3,5 * 5
- padding:零填充,Valid 与Same
- stride:步长,通常默认为1
- 计算公式
3.3.4.2 卷积运算过程
对于之前介绍的卷积运算过程,我们用一张动图来表示更好理解些。一下计算中,假设图片长宽相等,设为N
- 一个步长,3 X 3 卷积核运算
假设是一张5 X 5 的单通道图片,通过使用3 X 3 大小的卷积核运算得到一个 3 X 3大小的运算结果(图片像素数值仅供参考)
我们会发现进行卷积之后的图片变小了,假设N为图片大小,F为卷积核大小
相当于N - F + 1 = 5 - 3 + 1 = 3N−F+1=5−3+1=3
如果我们换一个卷积核大小或者加入很多层卷积之后,图像可能最后就变成了1 X 1 大小,这不是我们希望看到的结果。并且对于原始图片当中的边缘像素来说,只计算了一遍,二对于中间的像素会有很多次过滤器与之计算,这样导致对边缘信息的丢失。
- 缺点
- 图像变小
- 边缘信息丢失
3.3.4.3 padding-零填充
零填充:在图片像素的最外层加上若干层0值,若一层,记做p =1。
-
为什么增加的是0?
因为0在权重乘积和运算中对最终结果不造成影响,也就避免了图片增加了额外的干扰信息。
这张图中,还是移动一个像素,并且外面增加了一层0。那么最终计算结果我们可以这样用公式来计算:
5 + 2 * p - 3 + 1 = 55+2∗p−3+1=5
P为1,那么最终特征结果为5。实际上我们可以填充更多的像素,假设为2层,则
5 + 2 * 2 - 3 + 1 = 75+2∗2−3+1=7,这样得到的观察特征大小比之前图片大小还大。所以我们对于零填充会有一些选择,该填充多少?
3.3.4.4 Valid and Same卷积
有两种两种形式,所以为了避免上述情况,大家选择都是Same这种填充卷积计算方式
-
Valid :不填充,也就是最终大小为
- (N - F + 1) * (N - F + 1)(N−F+1)∗(N−F+1)
- Same:输出大小与原图大小一致,那么 NN变成了N + 2PN+2P
- (N + 2P - F + 1) * (N + 2P - F + 1)(N+2P−F+1)∗(N+2P−F+1)
那也就意味着,之前大小与之后的大小一样,得出下面的等式
所以当知道了卷积核的大小之后,就可以得出要填充多少层像素。
3.3.4.5 奇数维度的过滤器
通过上面的式子,如果F不是奇数而是偶数个,那么最终计算结果不是一个整数,造成0.5,1.5.....这种情况,这样填充不均匀,所以也就是为什么卷积核默认都去使用奇数维度大小
-
1*1,3*3, 5*5,7 7
-
另一个解释角度
- 奇数维度的过滤器有中心,便于指出过滤器的位置
当然这个都是一些假设的原因,最终原因还是在F对于计算结果的影响。所以通常选择奇数维度的过滤器,是大家约定成俗的结果,可能也是基于大量实验奇数能得出更好的结果。
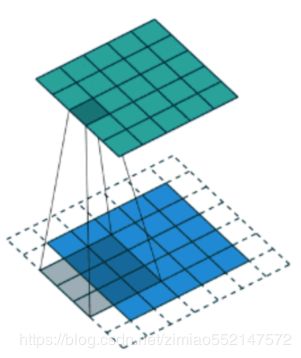
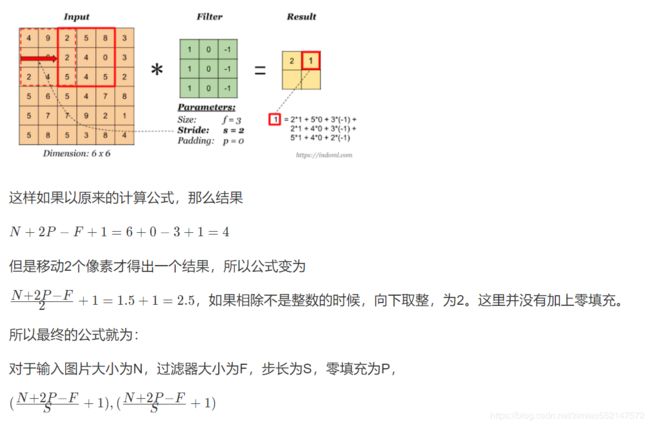
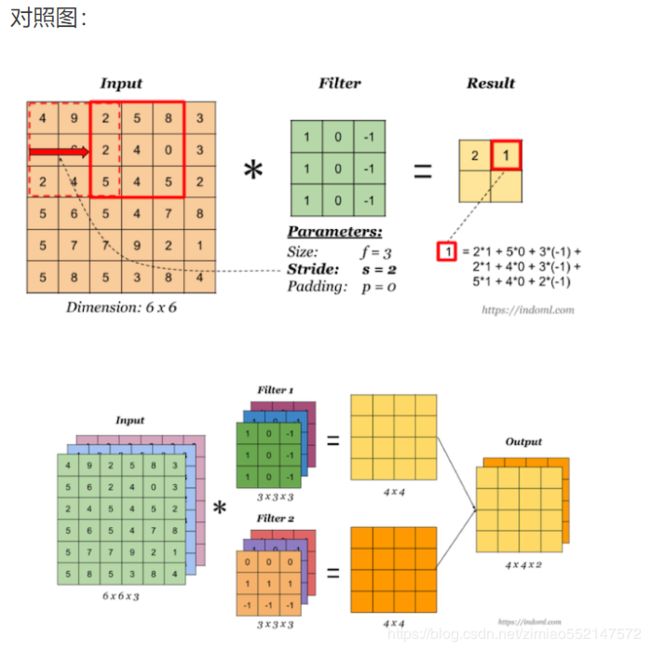
3.3.4.6 stride-步长
以上例子中我们看到的都是每次移动一个像素步长的结果,如果将这个步长修改为2,那结果如何?
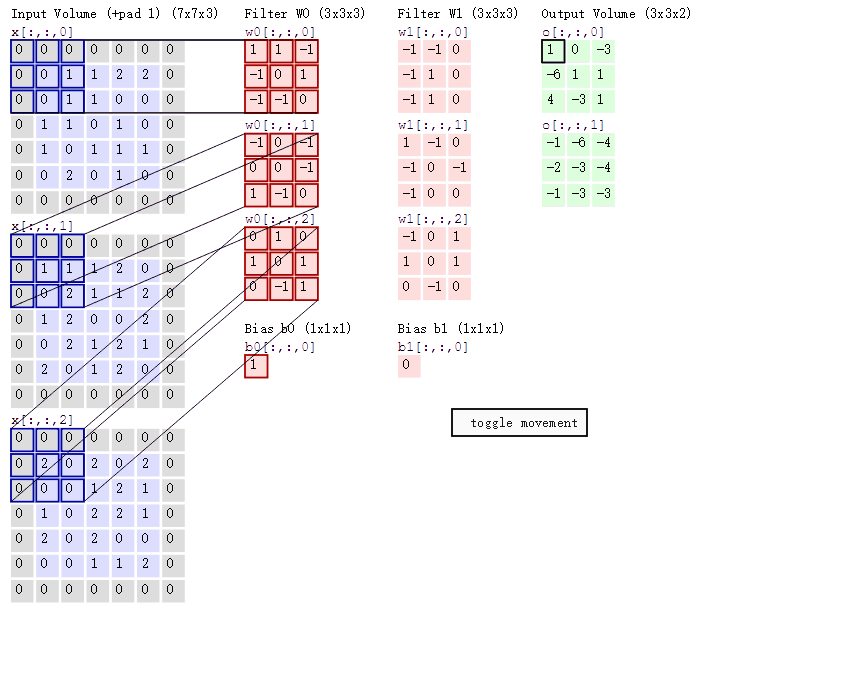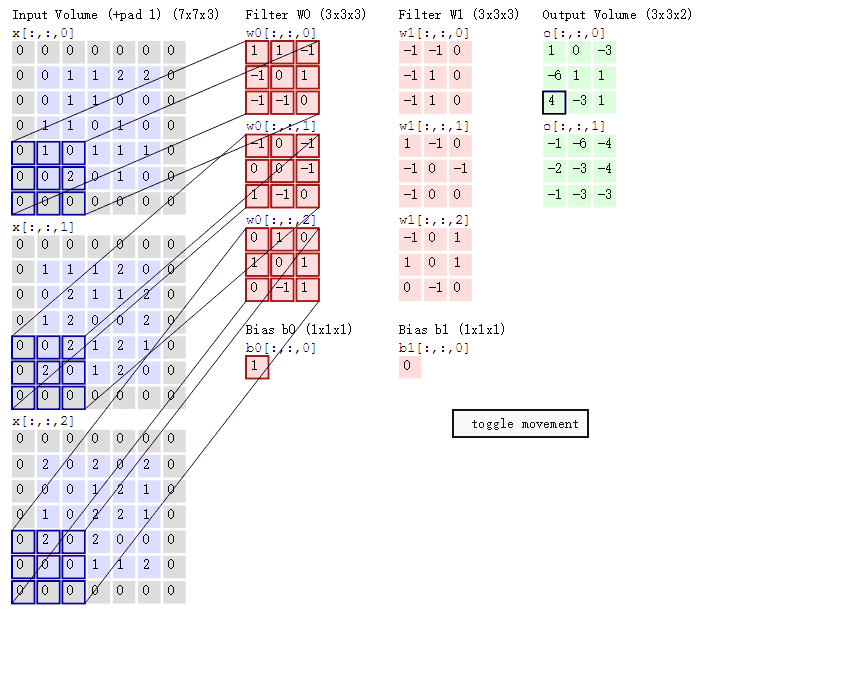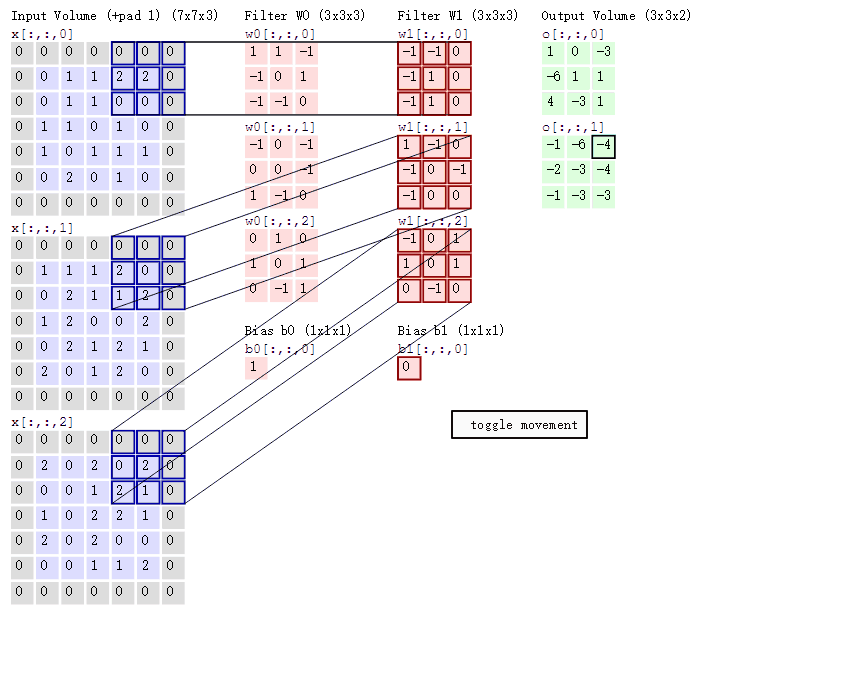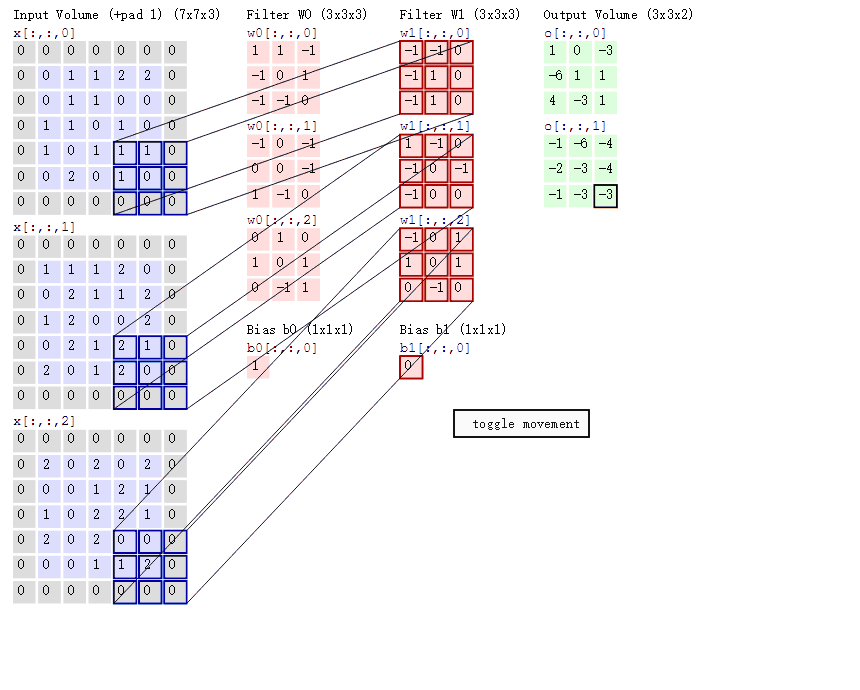
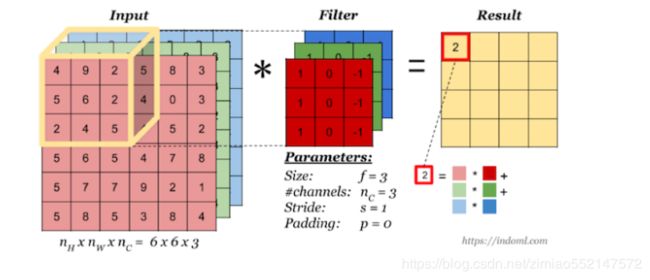
3.3.4.7 多通道卷积
当输入有多个通道(channel)时(例如图片可以有 RGB 三个通道),卷积核需要拥有相同的channel数,每个卷积核 channel 与输入层的对应 channel 进行卷积,将每个 channel 的卷积结果按位相加得到最终的 Feature Map。
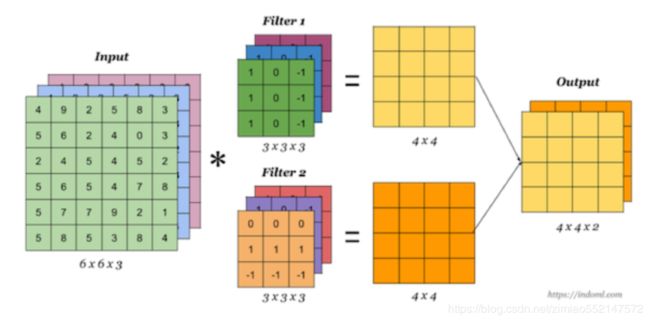
3.3.4.8 多卷积核
当有多个卷积核时,可以学习到多种不同的特征,对应产生包含多个 channel 的 Feature Map, 例如上图有两个 filter,所以 output 有两个 channel。这里的多少个卷积核也可理解为多少个神经元。
相当于我们把多个功能的卷积核的计算结果放在一起,比如水平边缘检测和垂直边缘检测器。
3.3.5 卷积总结
我们来通过一个例子看一下结算结果,以及参数的计算
3.3.5.1 设计单个卷积Filter的计算公式
3.3.5.2 卷积层实现代码介绍
以下代码主要通过numpy进行实现,再此我们只介绍实现过程理解,并不需要大家手写这样的代码,帮助理解原理过程。卷积实现的难点在于如何通过图片和过滤器去循环图片获得区域。
def conv_(img, conv_filter):
"""
卷积核计算操作
:param img: 图片数据
:param conv_filter: 卷积核
:return:
"""
# 1、获取卷积核的大小
filter_size = conv_filter.shape[1]
# 初始化卷积后的结果,给个较大的输出结果
result = np.zeros((img.shape))
# 2、对图片进行循环使用卷积操作(获取当前区域并使用过滤器进行相乘操作.)
# (1)r和c为特征图的下表,从0到特征图输出大小
for r in np.uint16(np.arange(filter_size/2.0, img.shape[0]-filter_size/2.0+1)):
for c in np.uint16(np.arange(filter_size/2.0, img.shape[1]-filter_size/2.0+1)):
# 取出过滤器大小的图片区域,从图片左上角开始
curr_region = img[r-np.uint16(np.floor(filter_size/2.0)):r+np.uint16(np.ceil(filter_size/2.0)),
c-np.uint16(np.floor(filter_size/2.0)):c+np.uint16(np.ceil(filter_size/2.0))]
# 图片当前区域与卷积核进行线性相乘
curr_result = curr_region * conv_filter
# 结果求和并保存,按照下表保存
conv_sum = np.sum(curr_result)
result[r, c] = conv_sum
# 裁剪矩阵
final_result = result[np.uint16(filter_size/2.0):result.shape[0]-np.uint16(filter_size/2.0),
np.uint16(filter_size/2.0):result.shape[1]-np.uint16(filter_size/2.0)]
return final_result
def conv(img, conv_filter):
"""
卷积过程实现
:param img: 图像
:param conv_filter: 卷积过滤器
:return:
"""
# 1、输入的参数大小做异常检测
# 检查输入的图片和卷积核是否一样大小
if len(img.shape) != len(conv_filter.shape) - 1:
print("Error: Number of dimensions in conv filter and image do not match.")
exit()
# 检查输入的图片的通道数和卷积的深度一样
if len(img.shape) > 2 or len(conv_filter.shape) > 3:
if img.shape[-1] != conv_filter.shape[-1]:
print("Error: Number of channels in both image and filter must match.")
sys.exit()
# 检查是否过滤器的长宽一样
if conv_filter.shape[1] != conv_filter.shape[2]:
print('Error: Filter must be a square matrix. I.e. number of rows and columns must match.')
sys.exit()
# 检查过滤器的维度是奇数
if conv_filter.shape[1] % 2 == 0:
print('Error: Filter must have an odd size. I.e. number of rows and columns must be odd.')
sys.exit()
# 2、初始化一个空的特征图来装入计算的结果
feature_maps = np.zeros((img.shape[0]-conv_filter.shape[1]+1,
img.shape[1]-conv_filter.shape[1]+1,
conv_filter.shape[0]))
# 3、图片的卷积完整操作(分别使用每一个过滤器进行过滤操作)
for filter_num in range(conv_filter.shape[0]):
print("Filter ", filter_num + 1)
# 获取当前的filter参数
curr_filter = conv_filter[filter_num, :]
# 当前filter进行卷积核计算操作
if len(curr_filter.shape) > 2:
# 对图片的每个channel进行卷积运算
conv_map = conv_(img[:, :, 0], curr_filter[:, :, 0])
for ch_num in range(1, curr_filter.shape[-1]):
conv_map = conv_map + conv_(img[:, :, ch_num], curr_filter[:, :, ch_num])
else:
# 只有一个filter的情况
conv_map = conv_(img, curr_filter)
feature_maps[:, :, filter_num] = conv_map
return feature_maps
# 使用过程
# 1、定义这层有两个卷积核,每个大小3x3(例子默认对黑白图片进行计算),默认一个步长,不零填充
l1_filter = np.zeros((2,3,3))
# 初始化参数
l1_filter[0, :, :] = np.array([[[-1, 0, 1],
[-1, 0, 1],
[-1, 0, 1]]])
l1_filter[1, :, :] = np.array([[[1, 1, 1],
[0, 0, 0],
[-1, -1, -1]]])
# 卷积计算
l1_feature_map = cnn.conv(img, l1_filter)3.3.5.3 池化层(Pooling)
池化层主要对卷积层学习到的特征图进行亚采样(subsampling)处理,主要由两种
-
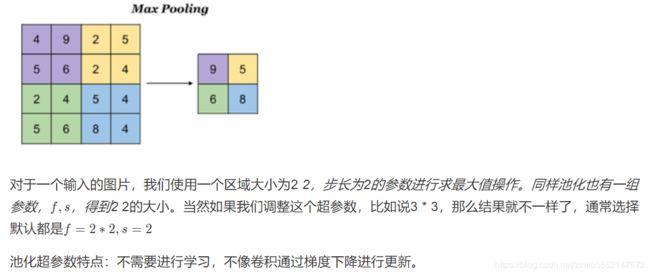
最大池化:Max Pooling,取窗口内的最大值作为输出
- 平均池化:Avg Pooling,取窗口内的所有值的均值作为输出
意义在于:
- 降低了后续网络层的输入维度,缩减模型大小,提高计算速度
- 提高了Feature Map 的鲁棒性,防止过拟合
3.3.5.4 最大池化层实现代码解释
def pooling(feature_map, size=2, stride=2):
"""
最大池化实现
:param feature_map: 特征图
:param size: 池化大小
:param stride: 步长
:return:
"""
# 1、准备池化层的输出初始化
pool_out = np.zeros((np.uint16((feature_map.shape[0] - size + 1) / stride + 1),
np.uint16((feature_map.shape[1] - size + 1) / stride + 1),
feature_map.shape[-1]))
# 2、循环取出每个方格当中的最大值作为新的输出
for map_num in range(feature_map.shape[-1]):
# 获取左上角横初始下标
r2 = 0
for r in np.arange(0, feature_map.shape[0] - size + 1, stride):
# 获取左上角纵初始下标
c2 = 0
for c in np.arange(0, feature_map.shape[1] - size + 1, stride):
pool_out[r2, c2, map_num] = np.max([feature_map[r:r + size, c:c + size, map_num]])
c2 = c2 + 1
r2 = r2 + 1
return pool_out3.3.5.5 全连接层
卷积层+激活层+池化层可以看成是CNN的特征学习/特征提取层,而学习到的特征(Feature Map)最终应用于模型任务(分类、回归):
- 先对所有 Feature Map 进行扁平化(flatten, 即 reshape 成 1 x N 向量)
- 再接一个或多个全连接层,进行模型学习
3.3.5.6 案例:通过封装的接口构建一个卷积网络
-
目的:通过上述的卷积、池化、接口完成一个卷积网络的识别过程
-
步骤:
- 1、读取图片处理图片、转换图片到灰度图
- 2、构建网络计算
- relu激活函数的实现
- 项目结构:
cnn_graph:为通过实现的CNN结构构建网络计算,numpyCNN是实现卷积、池化、relu激活函数接口文件
1、读取图片处理图片、转换图片到灰度图
# 导入包
import skimage.data
import numpy as np
from matplotlib import pyplot
import cnn
# 1、获取猫图片,转成单通道方便计算
img = skimage.data.chelsea()
img = skimage.color.rgb2gray(img)
# 定义过滤器(如上面介绍)
l1_filter = np.zeros((2,3,3))
l1_filter[0, :, :] = np.array([[[-1, 0, 1],
[-1, 0, 1],
[-1, 0, 1]]])
l1_filter[1, :, :] = np.array([[[1, 1, 1],
[0, 0, 0],
[-1, -1, -1]]])
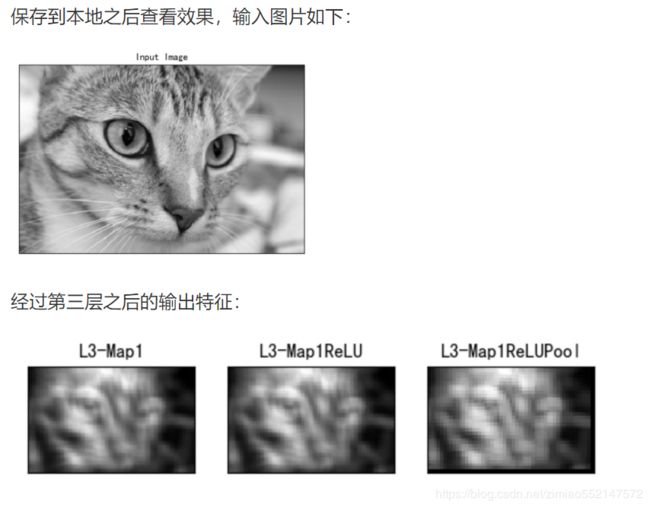
2、构建网络计算
这里构建三层网络结构,卷积、激活、池化
# 构建第一层
print("第一个卷积、池化层计算")
l1_feature_map = cnn.conv(img, l1_filter)
l1_feature_map_relu = cnn.relu(l1_feature_map)
l1_feature_map_relu_pool = cnn.pooling(l1_feature_map_relu, 2, 2)
# 构建第二层
print("第一个卷积、池化层计算")
l2_filter = np.random.rand(3, 5, 5, l1_feature_map_relu_pool.shape[-1])
l2_feature_map = cnn.conv(l1_feature_map_relu_pool, l2_filter)
l2_feature_map_relu = cnn.relu(l2_feature_map)
l2_feature_map_relu_pool = cnn.pooling(l2_feature_map_relu, 2, 2)
# 构建第三层
l3_filter = np.random.rand(1, 7, 7, l2_feature_map_relu_pool.shape[-1])
l3_feature_map = cnn.conv(l2_feature_map_relu_pool, l3_filter)
l3_feature_map_relu = cnn.relu(l3_feature_map)
l3_feature_map_relu_pool = cnn.pooling(l3_feature_map_relu, 2, 2)
- relu函数的实现
def relu(feature_map):
"""
relu激活函数实现
:param feature_map: 输入的特征图
:return:
"""
# 准备特征输入到relu激活函数
relu_out = np.zeros(feature_map.shape)
for map_num in range(feature_map.shape[-1]):
for r in np.arange(0, feature_map.shape[0]):
for c in np.arange(0, feature_map.shape[1]):
relu_out[r, c, map_num] = np.max([feature_map[r, c, map_num], 0])
return relu_out
- 最后的输出显示绘图
# 3、画出输出结果
fig0, ax0 = pyplot.subplots(nrows=1, ncols=1)
ax0.imshow(img).set_cmap("gray")
ax0.set_title("Input Image")
ax0.get_xaxis().set_ticks([])
ax0.get_yaxis().set_ticks([])
pyplot.savefig("in_img.png", bbox_inches="tight")
pyplot.close(fig0)
# 第三层卷积层输出结果显示
fig3, ax3 = pyplot.subplots(nrows=1, ncols=3)
ax3[0].imshow(l3_feature_map[:, :, 0]).set_cmap("gray")
ax3[0].get_xaxis().set_ticks([])
ax3[0].get_yaxis().set_ticks([])
ax3[0].set_title("L3-Map1")
ax3[1].imshow(l3_feature_map_relu[:, :, 0]).set_cmap("gray")
ax3[1].get_xaxis().set_ticks([])
ax3[1].get_yaxis().set_ticks([])
ax3[1].set_title("L3-Map1ReLU")
ax3[2].imshow(l3_feature_map_relu_pool[:, :, 0]).set_cmap("gray")
ax3[2].get_xaxis().set_ticks([])
ax3[2].get_yaxis().set_ticks([])
ax3[2].set_title("L3-Map1ReLUPool")
pyplot.savefig("L3.png", bbox_inches="tight")
pyplot.close(fig3)
3.3.6 卷积网络的感受野Receptive field (RF)以及计算
3.3.6.1 为什么学习感受野
感受野的感念前面提到是1962年Hubel和Wiesel通过对猫视觉皮层细胞的研究,提出了感受野(receptive field)的概念,Fukushima基于感受野概念提出的神经认知机(neocognitron)可以看作是卷积神经网络的第一个实现网络。
- 1、感受野的理解有助于对分类、检测网络架构的设计有深入的思考
- 2、感受野是卷积网络理解的基石,甚至自己去设计深度网络架构有着重要的作用。
3.3.6.2 感受野定义
- 定义:在卷积神经网络中,感受野的定义是 卷积神经网络每一层输出的特征图(feature map)上的像素点在原始图像上映射的区域大小。
- 或者也叫:感受野(Receptive Field)指的是神经网络中神经元“看到的”输入区域,在卷积神经网络中,feature map上某个元素的计算受输入图像上某个区域的影响,这个区域即该元素的感受野。
- 1、神经元感受野的值越大表示其能接触到的原始图像范围就越大,也意味着他可能蕴含更为全局、语义层次更高的特征;
- 2、神经元感受野的值越小则表示其所包含的特征越趋向于局部和细节。因此感受野的值可以大致用来判断每一层的抽象层次。
- 由于图像是二维的,具有空间信息,因此感受野的实质其实也是一个二维区域。但业界通常将感受野定义为一个正方形区域,因此也就使用边长来描述其大小
下面这张图表示感受野的理解:
3.3.6.3 计算
首先介绍cnn感受野计算公式:
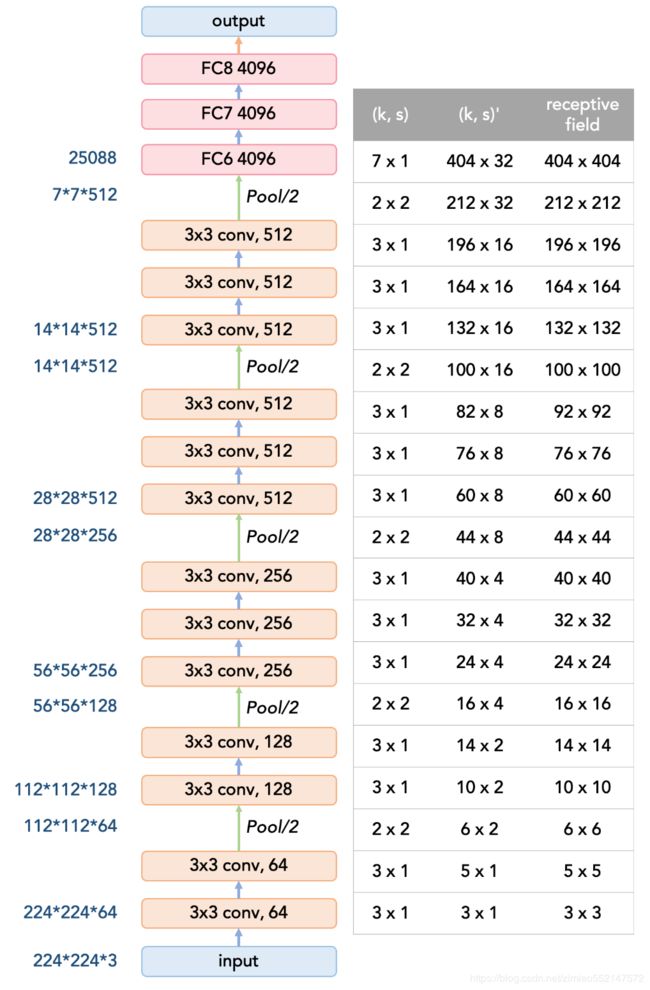
下图为后面要介绍的VGG感受野大小计算对应图:
3.3.7 总结
- 卷积神经网路的组成
- 卷积的计算过程
- 卷积过滤器个数
- 卷积过滤器大小
- 卷积过滤器步数
- 卷积过滤器零填充
- 池化的计算过程原理
- CNN结构的实现和构建实现程序
cnn.py
import numpy as np
import sys
def conv_(img, conv_filter):
"""
卷积核计算操作
:param img: 图片数据
:param conv_filter: 卷积核
:return:
"""
# 1、获取卷积核的大小
filter_size = conv_filter.shape[1]
# 初始化卷积后的结果
result = np.zeros((img.shape))
# 2、对图片进行循环使用卷积操作(获取当前区域并使用过滤器进行相乘操作.)
# (1)r和c为获取
for r in np.uint16(np.arange(filter_size/2.0, img.shape[0]-filter_size/2.0+1)):
for c in np.uint16(np.arange(filter_size/2.0, img.shape[1]-filter_size/2.0+1)):
curr_region = img[r-np.uint16(np.floor(filter_size/2.0)):r+np.uint16(np.ceil(filter_size/2.0)),
c-np.uint16(np.floor(filter_size/2.0)):c+np.uint16(np.ceil(filter_size/2.0))]
# 图片当前区域与卷积核进行线性相乘
curr_result = curr_region * conv_filter
# 结果求和并保存
conv_sum = np.sum(curr_result)
result[r, c] = conv_sum
# 裁剪结果矩阵的异常值
final_result = result[np.uint16(filter_size/2.0):result.shape[0]-np.uint16(filter_size/2.0),
np.uint16(filter_size/2.0):result.shape[1]-np.uint16(filter_size/2.0)]
return final_result
def conv(img, conv_filter):
"""
卷积过程实现
:param img: 图像
:param conv_filter: 卷积过滤器
:return:
"""
# 1、输入的参数大小做异常检测
# 检查输入的图片和卷积核是否一样大小
if len(img.shape) != len(conv_filter.shape) - 1:
print("Error: Number of dimensions in conv filter and image do not match.")
exit()
# 检查输入的图片的通道数和卷积的深度一样
if len(img.shape) > 2 or len(conv_filter.shape) > 3:
if img.shape[-1] != conv_filter.shape[-1]:
print("Error: Number of channels in both image and filter must match.")
sys.exit()
# 检查是否过滤器的长宽一样
if conv_filter.shape[1] != conv_filter.shape[2]:
print('Error: Filter must be a square matrix. I.e. number of rows and columns must match.')
sys.exit()
# 检查过滤器的维度是奇数
if conv_filter.shape[1] % 2 == 0:
print('Error: Filter must have an odd size. I.e. number of rows and columns must be odd.')
sys.exit()
# 2、初始化一个空的特征图来装入计算的结果
feature_maps = np.zeros((img.shape[0]-conv_filter.shape[1]+1,
img.shape[1]-conv_filter.shape[1]+1,
conv_filter.shape[0]))
# 3、图片的卷积完整操作(分别使用每一个过滤器进行过滤操作)
for filter_num in range(conv_filter.shape[0]):
print("Filter ", filter_num + 1)
# 获取当前的filter参数
curr_filter = conv_filter[filter_num, :]
# 当前filter进行卷积核计算操作
if len(curr_filter.shape) > 2:
# 对图片的每个channel进行卷积运算
conv_map = conv_(img[:, :, 0], curr_filter[:, :, 0])
for ch_num in range(1, curr_filter.shape[-1]):
conv_map = conv_map + conv_(img[:, :, ch_num], curr_filter[:, :, ch_num])
else:
# 只有一个filter的情况
conv_map = conv_(img, curr_filter)
feature_maps[:, :, filter_num] = conv_map
return feature_maps
def pooling(feature_map, size=2, stride=2):
"""
最大池化实现
:param feature_map: 特征图
:param size: 池化大小
:param stride: 步长
:return:
"""
# 1、准备池化层的输出初始化
pool_out = np.zeros((np.uint16((feature_map.shape[0] - size + 1) / stride + 1),
np.uint16((feature_map.shape[1] - size + 1) / stride + 1),
feature_map.shape[-1]))
# 2、循环取出每个方格当中的最大值作为新的输出
for map_num in range(feature_map.shape[-1]):
# 获取左上角横初始下标
r2 = 0
for r in np.arange(0, feature_map.shape[0] - size + 1, stride):
# 获取左上角纵初始下标
c2 = 0
for c in np.arange(0, feature_map.shape[1] - size + 1, stride):
pool_out[r2, c2, map_num] = np.max([feature_map[r:r + size, c:c + size, map_num]])
c2 = c2 + 1
r2 = r2 + 1
return pool_out
def relu(feature_map):
"""
relu激活函数实现
:param feature_map: 输入的特征图
:return:
"""
# 准备特征输入到relu激活函数
relu_out = np.zeros(feature_map.shape)
for map_num in range(feature_map.shape[-1]):
for r in np.arange(0, feature_map.shape[0]):
for c in np.arange(0, feature_map.shape[1]):
relu_out[r, c, map_num] = np.max([feature_map[r, c, map_num], 0])
return relu_out
cnn_graph.py
import skimage.data
import numpy as np
from matplotlib import pyplot
import cnn
def main():
# 1、读取图片数据进行处理
img = skimage.data.chelsea()
img = skimage.color.rgb2gray(img)
# 2、构建模型CNN,三层CNN,第一层:2个过滤器 第二层:三个过滤器5x5 第三层:1个过滤器7x7
# 第一层:
l1_filter = np.zeros((2, 3, 3))
l1_filter[0, :, :] = np.array([[[-1, 0, 1],
[-1, 0, 1],
[-1, 0, 1]]])
l1_filter[1, :, :] = np.array([[[1, 1, 1],
[0, 0, 0],
[-1, -1, -1]]])
l1_feature_map = cnn.conv(img, l1_filter)
l1_feature_map_relu = cnn.relu(l1_feature_map)
l1_feature_map_relu_pool = cnn.pooling(l1_feature_map_relu, 2, 2)
# 第一到三层卷积层输出结果显示
fig3, ax3 = pyplot.subplots(nrows=3, ncols=3)
ax3[0][0].imshow(l1_feature_map[:, :, 0]).set_cmap("gray")
ax3[0][0].get_xaxis().set_ticks([])
ax3[0][0].get_yaxis().set_ticks([])
ax3[0][0].set_title("L1-Map1")
ax3[0][1].imshow(l1_feature_map_relu[:, :, 0]).set_cmap("gray")
ax3[0][1].get_xaxis().set_ticks([])
ax3[0][1].get_yaxis().set_ticks([])
ax3[0][1].set_title("L1-Map1ReLU")
ax3[0][2].imshow(l1_feature_map_relu_pool[:, :, 0]).set_cmap("gray")
ax3[0][2].get_xaxis().set_ticks([])
ax3[0][2].get_yaxis().set_ticks([])
ax3[0][2].set_title("L1-Map1ReLUPool")
# 第二层
l2_filter = np.random.rand(3, 5, 5, l1_feature_map_relu_pool.shape[-1])
l2_feature_map = cnn.conv(l1_feature_map_relu_pool, l2_filter)
l2_feature_map_relu = cnn.relu(l2_feature_map)
l2_feature_map_relu_pool = cnn.pooling(l2_feature_map_relu, 2, 2)
ax3[1][0].imshow(l2_feature_map[:, :, 0]).set_cmap("gray")
ax3[1][0].get_xaxis().set_ticks([])
ax3[1][0].get_yaxis().set_ticks([])
ax3[1][0].set_title("L2-Map1")
ax3[1][1].imshow(l2_feature_map_relu[:, :, 0]).set_cmap("gray")
ax3[1][1].get_xaxis().set_ticks([])
ax3[1][1].get_yaxis().set_ticks([])
ax3[1][1].set_title("L2-Map1ReLU")
ax3[1][2].imshow(l2_feature_map_relu_pool[:, :, 0]).set_cmap("gray")
ax3[1][2].get_xaxis().set_ticks([])
ax3[1][2].get_yaxis().set_ticks([])
ax3[1][2].set_title("L2-Map1ReLUPool")
# 第三层
l3_filter = np.random.rand(1, 7, 7, l2_feature_map_relu_pool.shape[-1])
l3_feature_map = cnn.conv(l2_feature_map_relu_pool, l3_filter)
l3_feature_map_relu = cnn.relu(l3_feature_map)
l3_feature_map_relu_pool = cnn.pooling(l3_feature_map_relu, 2, 2)
# 3、显示处理之后的特征以及输出图片
# 3、画出输出结果
fig0, ax0 = pyplot.subplots(nrows=1, ncols=1)
ax0.imshow(img).set_cmap("gray")
ax0.set_title("Input Image")
ax0.get_xaxis().set_ticks([])
ax0.get_yaxis().set_ticks([])
pyplot.savefig("in_img.png", bbox_inches="tight")
pyplot.close(fig0)
ax3[2][0].imshow(l3_feature_map[:, :, 0]).set_cmap("gray")
ax3[2][0].get_xaxis().set_ticks([])
ax3[2][0].get_yaxis().set_ticks([])
ax3[2][0].set_title("L3-Map1")
ax3[2][1].imshow(l3_feature_map_relu[:, :, 0]).set_cmap("gray")
ax3[2][1].get_xaxis().set_ticks([])
ax3[2][1].get_yaxis().set_ticks([])
ax3[2][1].set_title("L3-Map1ReLU")
ax3[2][2].imshow(l3_feature_map_relu_pool[:, :, 0]).set_cmap("gray")
ax3[2][2].get_xaxis().set_ticks([])
ax3[2][2].get_yaxis().set_ticks([])
ax3[2][2].set_title("L3-Map1ReLUPool")
# 第三层卷积层输出结果显示
# fig3, ax3 = pyplot.subplots(nrows=1, ncols=3)
# ax3[0].imshow(l3_feature_map[:, :, 0]).set_cmap("gray")
# ax3[0].get_xaxis().set_ticks([])
# ax3[0].get_yaxis().set_ticks([])
# ax3[0].set_title("L3-Map1")
#
# ax3[1].imshow(l3_feature_map_relu[:, :, 0]).set_cmap("gray")
# ax3[1].get_xaxis().set_ticks([])
# ax3[1].get_yaxis().set_ticks([])
# ax3[1].set_title("L3-Map1ReLU")
#
# ax3[2].imshow(l3_feature_map_relu_pool[:, :, 0]).set_cmap("gray")
# ax3[2].get_xaxis().set_ticks([])
# ax3[2].get_yaxis().set_ticks([])
# ax3[2].set_title("L3-Map1ReLUPool")
pyplot.savefig("L3.png", bbox_inches="tight")
pyplot.close(fig3)
if __name__ == '__main__':
main()