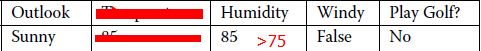一步一步详解ID3和C4.5的C++实现
1. 关于ID3和C4.5的原理介绍这里不赘述,网上到处都是,可以下载讲义c9641_c001.pdf或者参考李航的《统计学习方法》.(本文在博客园http://www.cnblogs.com/90zeng/p/ID3_C4_5.html同步发表)
2. 数据与数据处理
- 本文采用下面的训练数据:
- 数据处理:本文只采用了"Outlook", "Humidity", "Windy"三个属性,然后根据Humidity的值是否大于75,将Humidity的值归为两类,Play Golf 的值就是类别标签,只有yes 和 no两类
- 训练集是字符和数字的混合,这会给编程带来麻烦,所以首先把训练集用数字表示出来:
1 const unsigned att_num = 3; 2 const unsigned rule_num = 14; 3 string decision_tree_name("Play Golf ?"); 4 string attribute_names[] = {"Outlook", "Humidity", "Windy"}; 5 string attribute_values[] = {"Sunny", "Overcast", "Rainy", "> 75", "<= 75", "True", "False", "Yes", "No"}; 6 //训练集最后一列为分类标签,所以总列数为属性数加1 7 unsigned train_data[rule_num][att_num + 1] = { 8 {0, 3, 6, 8},{0, 3, 5, 8},{1, 3, 6, 7}, 9 {2, 3, 6, 7},{2, 3, 6, 7},{2, 4, 5, 8}, 10 {1, 4, 5, 7},{0, 3, 6, 8},{0, 4, 6, 7}, 11 {2, 3, 6, 7},{0, 4, 5, 7},{1, 3, 5, 7}, 12 {1, 4, 6, 7},{2, 3, 5, 8} 13 };以train_data的第一行{0, 3, 6, 8}为例解释:前三列值对应的属性与attribute_names中的元素分别对应,最后一列是类别标签的值,0 表示 attribute_values的第1个元素,即”Sunny“,类似3便是attribute_values的第4个元素"> 75",6 是 "False",8 是"No",所以{0, 3, 6, 8} 代表的实例就是:
其他实例都是以这样的方式数字化,方便编程.
3. 编写必要函数
因为ID3和C4.5都需要计算属性的信息增益,C4.5还需要计算属性的信息增益比,所正确编写这两个函数很重要,对比着讲义c9641_c001.pdf或者其他参考资料,编写出这两个函数.(代码最后附上)
4. 确定数据结构
这是最重要的一环,明确目的:构造一个决策树!这就直接决定了编程的正确或者难易,网上有很多例子,但是我觉得不够简洁,这里我采用一种简单且容易理解的方式:
1 struct Tree{
2 unsigned root;//节点属性值
3 vector branches;//节点可能取值
4 vector children; //孩子节点
5 };
每一个决策树都是由根节点开始,然后有很多分支,分支连接着孩子节点,而每一个孩子节点以及这个孩子节点对应的所有子孙又可以组成一棵树,这是一个不断递归的过程,所以采用了上面的数据结构.
5. 构造决策树
有了上面的基础,开始着手构造决策树,根据规则选出某一属性作为根节点,根据根节点的取值确定分支,然后构造孩子节点,根据上面的陈述可以知道,每一个孩子节点及其后面的子孙又是一棵树,所以这是一个递归操作,即采用前面同样的方式来构造这个子树,以此类推。
6. 打印决策树
因为树的结构是递归的,所以打印决策树同样是一个递归的过程。
7. 代码实现
1 /*************************************************
2 Copyright:1.0
3 Author:太白路上的小混混
4 Date:2014-11-25
5 Description:ID3/C4.5 algorithm
6 **************************************************/
7
8 #include
9 #include
10 #include
11 #include <string>
12 #include
13 using namespace std;
14
15
16 const unsigned att_num = 3;
17 const unsigned rule_num = 14;
18 string decision_tree_name("Play Golf ?");
19 string attribute_names[] = {"Outlook", "Humidity", "Windy"};
20 string attribute_values[] = {"Sunny", "Overcast", "Rainy", "> 75", "<= 75", "True", "False", "Yes", "No"};
21 //训练集最后一列为分类标签,所以总列数为属性数加1
22 unsigned train_data[rule_num][att_num + 1] = {
23 {0, 3, 6, 8},{0, 3, 5, 8},{1, 3, 6, 7},
24 {2, 3, 6, 7},{2, 3, 6, 7},{2, 4, 5, 8},
25 {1, 4, 5, 7},{0, 3, 6, 8},{0, 4, 6, 7},
26 {2, 3, 6, 7},{0, 4, 5, 7},{1, 3, 5, 7},
27 {1, 4, 6, 7},{2, 3, 5, 8}
28 };
29
30
31
32
33 /*************************************************
34 Function: unique()
35 Description: 将vector中重复元素合并,只保留一个
36 Calls: 无
37 Input: vector
38 Output: vector
39 *************************************************/
40 template
41 vector unique(vector vals)
42 {
43 vector unique_vals;
44 vector::iterator itr;
45 vector::iterator subitr;
46
47 int flag = 0;
48 while( !vals.empty() )
49 {
50 unique_vals.push_back(vals[0]);
51 itr = vals.begin();
52 subitr = unique_vals.begin() + flag;
53 while ( itr != vals.end())
54 {
55 if (*subitr == *itr)
56 itr = vals.erase(itr);
57 else
58 itr++;
59 }
60 flag++;
61 }
62 return unique_vals;
63 }
64
65 /*************************************************
66 Function: log2()
67 Description: 计算一个数值得以2为底的对数
68 Calls: 无
69 Input: double
70 Output: double
71 *************************************************/
72
73 double log2(double n)
74 {
75 return log10(n) / log10(2.0);
76 }
77
78 /*************************************************
79 Function: compute_entropy()
80 Description: 根据属性的取值,计算该属性的熵
81 Calls: unique(),log2(),count(),其中count()
82 在STL的algorithm库中
83 Input: vector
84 Output: double
85 *************************************************/
86 double compute_entropy(vector v)
87 {
88 vector unique_v;
89 unique_v = unique(v);
90
91 vector::iterator itr;
92 itr = unique_v.begin();
93
94 double entropy = 0.0;
95 auto total = v.size();
96 while(itr != unique_v.end())
97 {
98 double cnt = count(v.begin(), v.end(), *itr);
99 entropy -= cnt / total * log2(cnt / total);
100 itr++;
101 }
102 return entropy;
103 }
104
105 /*************************************************
106 Function: compute_gain()
107 Description: 计算数据集中所有属性的信息增益
108 Calls: compute_entropy(),unique()
109 Input: vector >
110 相当于一个二维数组,存储着训练数据集
111 Output: vector 存储着所有属性的信息
112 增益
113 *************************************************/
114 vector<double> compute_gain(vector > truths)
115 {
116 vector<double> gain(truths[0].size() - 1, 0);
117 vector attribute_vals;
118 vector labels;
119 for(unsigned j = 0; j < truths.size(); j++)
120 {
121 labels.push_back(truths[j].back());
122 }
123
124 for(unsigned i = 0; i < truths[0].size() - 1; i++)//最后一列是类别标签,没必要计算信息增益
125 {
126 for(unsigned j = 0; j < truths.size(); j++)
127 attribute_vals.push_back(truths[j][i]);
128
129 vector unique_vals = unique(attribute_vals);
130 vector::iterator itr = unique_vals.begin();
131 vector subset;
132 while(itr != unique_vals.end())
133 {
134 for(unsigned k = 0; k < truths.size(); k++)
135 {
136 if (*itr == attribute_vals[k])
137 {
138 subset.push_back(truths[k].back());
139 }
140 }
141 double A = (double)subset.size();
142 gain[i] += A / truths.size() * compute_entropy(subset);
143 itr++;
144 subset.clear();
145 }
146 gain[i] = compute_entropy(labels) - gain[i];
147 attribute_vals.clear();
148 }
149 return gain;
150 }
151
152 /*************************************************
153 Function: compute_gain_ratio()
154 Description: 计算数据集中所有属性的信息增益比
155 C4.5算法中用到
156 Calls: compute_gain();compute_entropy()
157 Input: 训练数据集
158 Output: 信息增益比
159 *************************************************/
160 vector<double> compute_gain_ratio(vector > truths)
161 {
162 vector<double> gain = compute_gain(truths);
163 vector<double> entropies;
164 vector<double> gain_ratio;
165
166 for(unsigned i = 0; i < truths[0].size() - 1; i++)//最后一列是类别标签,没必要计算信息增益比
167 {
168 vector attribute_vals(truths.size(), 0);
169 for(unsigned j = 0; j < truths.size(); j++)
170 {
171 attribute_vals[j] = truths[j][i];
172 }
173 double current_entropy = compute_entropy(attribute_vals);
174 if (current_entropy)
175 {
176 gain_ratio.push_back(gain[i] / current_entropy);
177 }
178 else
179 gain_ratio.push_back(0.0);
180
181 }
182 return gain_ratio;
183 }
184
185 /*************************************************
186 Function: find_most_common_label()
187 Description: 找出数据集中最多的类别标签
188
189 Calls: count();
190 Input: 数据集
191 Output: 类别标签
192 *************************************************/
193 template
194 T find_most_common_label(vector > data)
195 {
196 vector labels;
197 for (unsigned i = 0; i < data.size(); i++)
198 {
199 labels.push_back(data[i].back());
200 }
201 vector:: iterator itr = labels.begin();
202 T most_common_label;
203 unsigned most_counter = 0;
204 while (itr != labels.end())
205 {
206 unsigned current_counter = count(labels.begin(), labels.end(), *itr);
207 if (current_counter > most_counter)
208 {
209 most_common_label = *itr;
210 most_counter = current_counter;
211 }
212 itr++;
213 }
214 return most_common_label;
215 }
216
217 /*************************************************
218 Function: find_attribute_values()
219 Description: 根据属性,找出该属性可能的取值
220
221 Calls: unique();
222 Input: 属性,数据集
223 Output: 属性所有可能的取值(不重复)
224 *************************************************/
225 template
226 vector find_attribute_values(T attribute, vector > data)
227 {
228 vector values;
229 for (unsigned i = 0; i < data.size(); i++)
230 {
231 values.push_back(data[i][attribute]);
232 }
233 return unique(values);
234 }
235
236 /*************************************************
237 Function: drop_one_attribute()
238 Description: 在构建决策树的过程中,如果某一属性已经考察过了
239 那么就从数据集中去掉这一属性,此处不是真正意义
240 上的去掉,而是将考虑过的属性全部标记为110,当
241 然可以是其他数字,只要能和原来训练集中的任意数
242 字区别开来即可
243 Calls: unique();
244 Input: 属性,数据集
245 Output: 属性所有可能的取值(不重复)
246 *************************************************/
247 template
248 vector > drop_one_attribute(T attribute, vector > data)
249 {
250 vector > new_data(data.size(),vector(data[0].size() - 1, 0));
251 for (unsigned i = 0; i < data.size(); i++)
252 {
253 data[i][attribute] = 110;
254 }
255 return data;
256 }
257
258
259 struct Tree{
260 unsigned root;//节点属性值
261 vector branches;//节点可能取值
262 vector children; //孩子节点
263 };
264
265 /*************************************************
266 Function: build_decision_tree()
267 Description: 递归构建决策树
268
269 Calls: unique(),count(),
270 find_most_common_label()
271 compute_gain()(ID3),
272 compute_gain_ratio()(C4.5),
273 find_attribute_values(),
274 drop_one_attribute(),
275 build_decision_tree()(递归,
276 当然要调用函数本身)
277 Input: 训练数据集,一个空决策树
278 Output: 无
279 *************************************************/
280 void build_decision_tree(vector > examples, Tree &tree)
281 {
282 //第一步:判断所有实例是否都属于同一类,如果是,则决策树是单节点
283 vector labels(examples.size(), 0);
284 for (unsigned i = 0; i < examples.size(); i++)
285 {
286 labels[i] = examples[i].back();
287 }
288 if (unique(labels).size() == 1)
289 {
290 tree.root = labels[0];
291 return;
292 }
293
294 //第二步:判断是否还有剩余的属性没有考虑,如果所有属性都已经考虑过了,
295 //那么此时属性数量为0,将训练集中最多的类别标记作为该节点的类别标记
296 if (count(examples[0].begin(),examples[0].end(),110) == examples[0].size() - 1)//只剩下一列类别标记
297 {
298 tree.root = find_most_common_label(examples);
299 return;
300 }
301 //第三步:在上面两步的条件都判断失败后,计算信息增益,选择信息增益最大
302 //的属性作为根节点,并找出该节点的所有取值
303
304 vector<double> standard = compute_gain(examples);
305
306 //要是采用C4.5,将上面一行注释掉,把下面一行的注释去掉即可
307 //vector standard = compute_gain_ratio(examples);
308 tree.root = 0;
309 for (unsigned i = 0; i < standard.size(); i++)
310 {
311 if (standard[i] >= standard[tree.root] && examples[0][i] != 110)
312 tree.root = i;
313 }
314
315
316 tree.branches = find_attribute_values(tree.root, examples);
317 //第四步:根据节点的取值,将examples分成若干子集
318 vector > new_examples = drop_one_attribute(tree.root, examples);
319 vector > subset;
320 for (unsigned i = 0; i < tree.branches.size(); i++)
321 {
322 for (unsigned j = 0; j < examples.size(); j++)
323 {
324 for (unsigned k = 0; k < examples[0].size(); k++)
325 {
326 if (tree.branches[i] == examples[j][k])
327 subset.push_back(new_examples[j]);
328 }
329 }
330 // 第六步:对每一个子集递归调用build_decision_tree()函数
331 Tree new_tree;
332 build_decision_tree(subset,new_tree);
333 tree.children.push_back(new_tree);
334 subset.clear();
335 }
336 }
337
338 /*************************************************
339 Function: print_tree()
340 Description: 从第根节点开始,逐层将决策树输出到终
341 端显示
342
343 Calls: print_tree();
344 Input: 决策树,层数
345 Output: 无
346 *************************************************/
347 void print_tree(Tree tree,unsigned depth)
348 {
349 for (unsigned d = 0; d < depth; d++) cout << "\t";
350 if (!tree.branches.empty()) //不是叶子节点
351 {
352 cout << attribute_names[tree.root] << endl;
353
354 for (unsigned i = 0; i < tree.branches.size(); i++)
355 {
356 for (unsigned d = 0; d < depth + 1; d++) cout << "\t";
357 cout << attribute_values[tree.branches[i]] << endl;
358 print_tree(tree.children[i],depth + 2);
359 }
360 }
361 else //是叶子节点
362 {
363 cout << attribute_values[tree.root] << endl;
364 }
365
366 }
367
368
369 int main()
370 {
371 vector > rules(rule_num, vector(att_num + 1, 0));
372 for(unsigned i = 0; i < rule_num; i++)
373 {
374 for(unsigned j = 0; j <= att_num; j++)
375 rules[i][j] = train_data[i][j];
376 }
377 Tree tree;
378 build_decision_tree(rules, tree);
379 cout << decision_tree_name << endl;
380 print_tree(tree,0);
381 return 0;
382 }
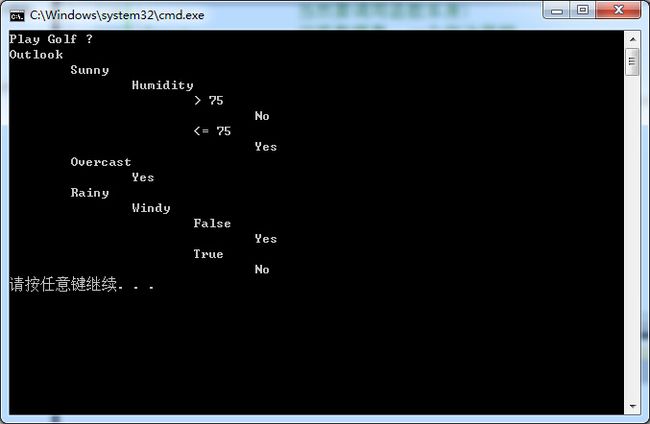
8.运行结果:
前者是采用ID3运行的结果,后者是讲义c9641_c001.pdf给出的构造的决策树,二者一致,验证了程序的正确性.
9.总结
所谓”百鸟在林,不如一鸟在手“, ID3和C4.5的思想都很简单,容易理解,但是在实现的的过程中由于数据结构的确定和递归调用等问题,还是调试了很久,收获很多,实践出真知!