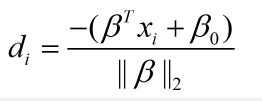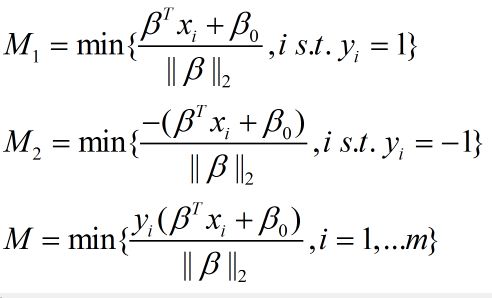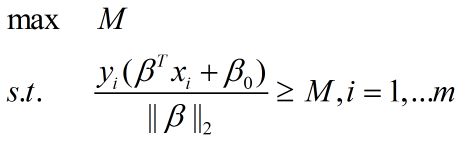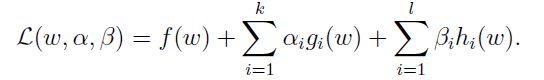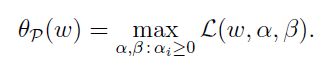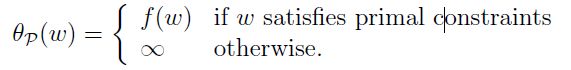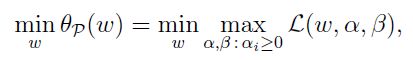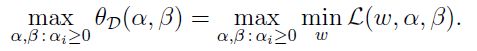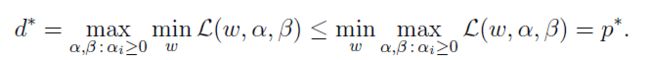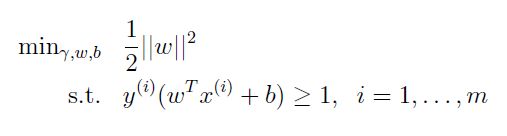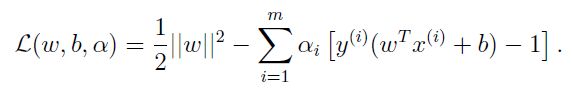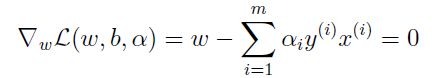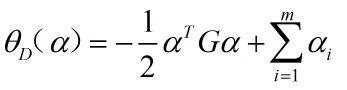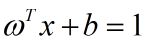SVM支撑向量机详解(一)

一、SVM简介

SVM(Support Vector Machine)被认为是现存的最好的监督学习算法之一，甚至有人认为它就是最好的。Ng为了讲清楚这个算法，先是从最优间隔分类器开始，再到KKT条件原问题和对偶问题，最后引出SVM的概念和求解方法。我按我的理解来，可能细节有点不一样，但最后是殊途同归。

二、最优间隔分类算法

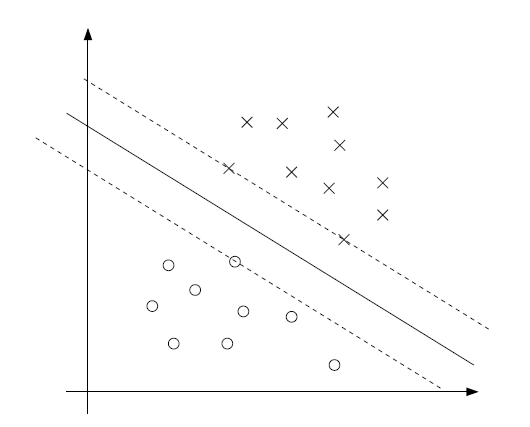
假设有两个数据集{(xi,yi):i=1,...m},其中xi是p维向量，p为特征维数，而yi∈{-1,1}，i=1,...,m是样本数量。并且假设该数据集是线性可分的。如下图：

上面是正样本，下面是负样本，中间是一个分割超平面。上图所示即为当p=2时，xi为二维向量，代表的是平面上的点，如果p等于一个很大的数，用图形是无法形象表达的。

因为数据是线性可分的，即

计算任一点xi到超平面的距离，根据点到平面距离公式：

正样本点：

负样本点：

（因为距离不可能为负数，所以在前面添加一个负号）

令：

M被称为几何间隔。

试想一下，一个好的分类超平面，肯定是两边的点到其距离都尽可能的小。所以最优间隔分类器 的目标函数为：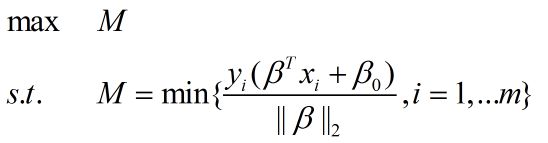

这个意义也是明显的，最优的分类器肯定使所有样本到超平面的最小距离最大化。上述最优化问题等价为：

两边同时除以M,将约束进一步简化为：

所以，最优间隔分类算法的目标函数又变为：

这是个QP(这是一个凸二次规划，可以用现成软件求解)问题。

三、Lagrange乘子与其对偶

我们知道，对于无约束凸优化问题，稳定点即为极小点，但是对于类似于上面的最优间隔分类算法，明显是个约束优化，此时应该如何解决呢，所以这里引入KKT条件及对偶，是用来解决约束convex问题的基石。

假设我们有如下优化问题：

为了将其间接的转化成无约束优化问题，将原问题和条件进行一定的加权整合，加权因子α和β即为Lagrange乘子，得到Lagrange函数为：

写出Lagrange对偶问题：

为什么是这个式子呢，我们可以看到，基于α大于零和β无限制这个条件，如果g(w)和h(w)不满足条件，则该式就会趋于无穷大，即：

根据对偶原理，原问题为min max，对偶问题即为max min（这里可参见数学规划基础）可以写出对偶问题为：

且同时满足对偶定理：

d*和p*分别为对偶问题和原问题的最优值。相应的最优解为w*，α*，β*，当满足某些正则性条件时（比较复杂这里不做详细说明）， 在最优解处就有KKT条件成立：

这是局部最优解的必要条件。

四、SVM算法

在介绍完最优间隔分类器和Lagrange对偶及kkt条件之后，我们就可以引出SVM的真面目了，SVM其实就是最优间隔分类的对偶问题。最优间隔分类的目标函数为：

（4-1）

即不等式约束为：

（4-2）

所以该问题的Lagrange函数为：

（4-3）

对偶问题为：

（4-4）

由于内层参数w为p维实向量，b为实数，所以内层为无约束优化问题，直接求导(或者说根据kkt条件)。有：

(4-5)

（4-6）

将(4-5)和(4-6)式代入(4-3)，得：

(4-7)

上式就是L(w,b;α)的最小值minL(w,b:α)，令

，则有

(4-8)

所以SVM问题为：

(4-9)

这是个很简单的二次规划问题，可以借助优化软件求解得最优解α*向量，则

下面就根据这个式子解释支撑向量的由来：

根据KKT互补条件，不等于0对应着不等式约束(4-2)严格成立，不等式(4-2)对应的边界为下图中两条虚线，分别

为和，

在这两条边界之外的向量称为支撑向量，即超平面最后的法向量w*是由支撑向量的线性组合而成，组合系数即为对应的不为0的lagrange最优乘子α*，所以(4-9)问题解出的即为支撑向量！

五、代码实现

opencv2.4.9中支持SVM算法，这里暂时给出线性SVM算法的代码。基于opencv实现的啦，比较简单。

#include 
#include 
#include 

using namespace cv;

int main()
{
	// Data for visual representation
	int width = 512, height = 512;
	Mat image = Mat::zeros(height, width, CV_8UC3);

	// Set up training data
	float labels[4] = { 1.0, -1.0, -1.0, -1.0 };
	Mat labelsMat(3, 1, CV_32FC1, labels);

	float trainingData[4][2] = { { 501, 10 }, { 255, 10 }, { 501, 255 }, { 10, 501 } };
	Mat trainingDataMat(3, 2, CV_32FC1, trainingData);

	// Set up SVM's parameters
	CvSVMParams params;
	params.svm_type = CvSVM::C_SVC;
	params.kernel_type = CvSVM::LINEAR;
	params.term_crit = cvTermCriteria(CV_TERMCRIT_ITER, 100, 1e-6);

	// Train the SVM
	CvSVM SVM;
	SVM.train(trainingDataMat, labelsMat, Mat(), Mat(), params);

	Vec3b green(0, 255, 0), blue(255, 0, 0);
	// Show the decision regions given by the SVM
	for (int i = 0; i < image.rows; ++i)
		for (int j = 0; j < image.cols; ++j)
		{
		Mat sampleMat = (Mat_(1, 2) << i, j);
		float response = SVM.predict(sampleMat);

		if (response == 1)
			image.at(j, i) = green;
		else if (response == -1)
			image.at(j, i) = blue;
		}

	// Show the training data
	int thickness = -1;
	int lineType = 8;
	circle(image, Point(501, 10), 5, Scalar(0, 0, 0), thickness, lineType);
	circle(image, Point(255, 10), 5, Scalar(255, 255, 255), thickness, lineType);
	circle(image, Point(501, 255), 5, Scalar(255, 255, 255), thickness, lineType);
	circle(image, Point(10, 501), 5, Scalar(255, 255, 255), thickness, lineType);

	// Show support vectors
	thickness = 2;
	lineType = 8;
	int c = SVM.get_support_vector_count();

	for (int i = 0; i < c; ++i)
	{
		const float* v = SVM.get_support_vector(i);
		circle(image, Point((int)v[0], (int)v[1]), 6, Scalar(128, 128, 128), thickness, lineType);
	}

	imwrite("result.png", image);        // save the image 

	imshow("SVM Simple Example", image); // show it to the user
	waitKey(0);

}