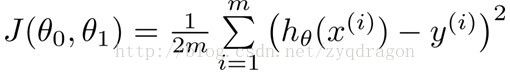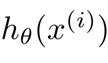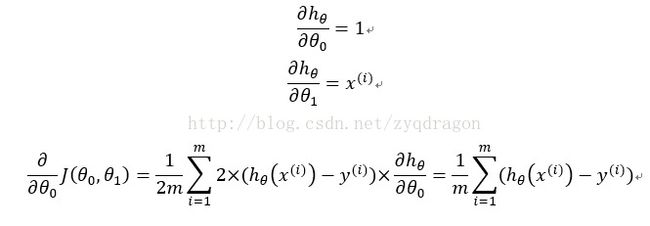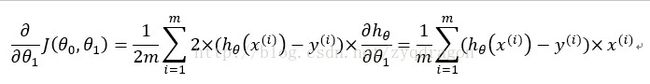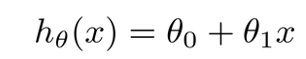利用梯度下降法实现线性回归的算法及matlab实现
利用梯度下降法实现线性回归的算法及matlab实现
1. 线性回归算法概述
线性回归属于监督学习，因此方法和监督学习应该是一样的，先给定一个训练集，根据这个训练集学习出一个线性函数，然后测试这个函数训练的好不好（即此函数是否足够拟合训练集数据），挑选出最好的函数（cost function最小）即可；
注意：
(1)因为是线性回归，所以学习到的函数为线性函数，即直线函数；
(2)线性回归可分为单变量线性回归和多变量线性回归；对于单变量线性回归而言，只有一个输入变量x；
(1). 单变量线性回归
我们能够给出单变量线性回归的模型：
我们常称x为feature，h(x)为hypothesis；上述模型中的θ0和θ1在代码中分别用theta0和theta1表示。
从上面“方法”中，我们肯定有一个疑问，怎么样能够看出线性函数拟合的好不好呢？我们需要使用到Cost Function（代价函数），代价函数越小，说明线性回归地越好（和训练集拟合地越好），当然最小就是0，即完全拟合。cost Function的内部构造如下面公式所述：
其中：
x(i)表示向量x中的第i个元素；
y(i)表示向量y中的第i个元素；
表示已知的假设函数；
m为训练集的数量；
虽然给定一个函数，我们能够根据cost function知道这个函数拟合的好不好，但是毕竟函数有这么多，总不可能一个一个试吧？因此我们引出了梯度下降：能够找出cost function函数的最小值；
梯度下降原理：将函数比作一座山，我们站在某个山坡上，往四周看，从哪个方向向下走一小步，能够下降的最快；当然解决问题的方法有很多，梯度下降只是其中一个，还有一种方法叫Normal Equation；
方法：
(1)先确定向下一步的步伐大小，我们称为Learning rate (alpha)；
(2)任意给定一个初始值：
(用theta0和theta1表示)；
(3)确定一个向下的方向，并向下走预先规定的步伐，并更新；
(4)当下降的高度小于某个定义的值，则停止下降；
算法：
特点：
(1)初始点不同，获得的最小值也不同，因此梯度下降求得的只是局部最小值；
(2)越接近最小值时，下降速度越慢；
梯度下降能够求出一个函数的最小值；
线性回归需要使得cost function的最小；
因此我们能够对cost function运用梯度下降，即将梯度下降和线性回归进行整合，如下图所示：
上式中右边的公式推导过程如下：
从上面的推导中可以看出，要想满足梯度下降的条件，则项后面必须乘以对应的输入信号。
梯度下降是通过不停的迭代，而我们比较关注迭代的次数，因为这关系到梯度下降的执行速度，为了减少迭代次数，因此引入了Feature Scaling。
(2). Feature Scaling
此种方法应用于梯度下降，为了加快梯度下降的执行速度；
思想：将各个feature的值标准化，使得取值范围大致都在-1<=x<=1之间；
(3). 常用的方法是Mean Normalization(均值归一化处理)
或者：
[X-mean(X)]/std(X);
(4). 收获汇总
学习速率的大小对于系统是否收敛有决定性的影响。如果学习速率太大，那么可能导致系统震荡发撒；如果学习速率太小，那么可能导致系统收敛速度变慢。
(a) 根据给定数据架设预测函数h(x)
(b) 计算代价函数J
(c) 计算各参数偏导
(d) 更新参数
(e) 重复2~4直到代价函数跟新的步长小于设定值或者是重复次数达到预设值。
为了在相同学习速率的前提下加快相同收敛，可采用训练数据归一化的方法来对样本数据进行预处理。采用均值均值归一化处理后，缩小了原来数据的变化幅度，从而可极大地提高学习速率，从而提高了梯度下降的执行速度。在第四部分的matlab代码中，对输入值向量进行归一化处理之后，将学习速率从0.01提高到1.9,从而将获得系统收敛的epoch次数由10000次减少到300次。
2. Matlab实现单变量梯度下降的线性回归
(1). Gradient descend code 1
clear all
clc
% training sample data;
p0=3;
p1=7;
x=1:3;
y=p0+p1*x;
num_sample=size(y,2);
% gradient descending process
% initial values of parameters
theta0=1;
theta1=3;
%learning rate
alpha=0.02;
% if alpha is too large, the final error will be much large.
% if alpha is too small, the convergence will be slow
epoch=500;
for k=1:epoch
v_k=k
h_theta_x=theta0+theta1*x; % hypothesis function
Jcost(k)=((h_theta_x(1)-y(1))^2+(h_theta_x(2)-y(2))^2+(h_theta_x(3)-y(3))^2)/num_sample
theta0=theta0-alpha*((h_theta_x(1)-y(1))+(h_theta_x(2)-y(2))+(h_theta_x(3)-y(3)))/num_sample;
theta1=theta1-alpha*((h_theta_x(1)-y(1))*x(1)+(h_theta_x(2)-y(2))*x(2)+(h_theta_x(3)-y(3))*x(3))/num_sample;
end
plot(Jcost)
(5). Gradient descend code 2
clear all
clc
% training sample data;
p0=26;
p1=73;
x=1:3;
y=p0+p1*x;
num_sample=size(y,2);
% gradient descending process
% initial values of parameters
theta0=1;
theta1=3;
%learning rate
alpha=0.08;
% if alpha is too large, the final error will be much large.
% if alpha is too small, the convergence will be slow
epoch=500;
for k=1:epoch
v_k=k
h_theta_x=theta0+theta1*x; % hypothesis function
Jcost(k)=((h_theta_x(1)-y(1))^2+(h_theta_x(2)-y(2))^2+(h_theta_x(3)-y(3))^2)/num_sample;
theta0=theta0-alpha*((h_theta_x(1)-y(1))+(h_theta_x(2)-y(2))+(h_theta_x(3)-y(3)))/num_sample;
theta1=theta1-alpha*((h_theta_x(1)-y(1))*x(1)+(h_theta_x(2)-y(2))*x(2)+(h_theta_x(3)-y(3))*x(3))/num_sample;
% disp('*********comp 1**************');
r1=((h_theta_x(1)-y(1))+(h_theta_x(2)-y(2))+(h_theta_x(3)-y(3)));
r2=sum(h_theta_x-y);
% disp('*********comp 2**************');
r3=((h_theta_x(1)-y(1))^2+(h_theta_x(2)-y(2))^2+(h_theta_x(3)-y(3))^2);
r4=sum((h_theta_x-y).^2);
% disp('*********comp 3**************');
r5=((h_theta_x(1)-y(1))*x(1)+(h_theta_x(2)-y(2))*x(2)+(h_theta_x(3)-y(3))*x(3));
r6=sum((h_theta_x-y).*x);
if((r1~=r2)||(r3~=r4)||(r5~=r6))
disp('***wrong result******')
end
end
plot(Jcost)
3. 线性回归与单神经元的对应关系
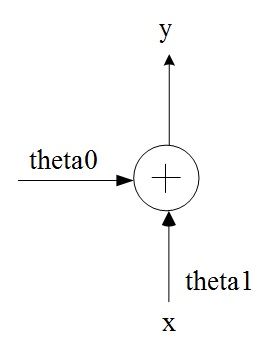
单变量线性回归的模型：
与单神经元模型具有对应的关系，可实现相同的功能。其中θ0相当于单神经元的偏置值bias值，x相当于单神经元的单个输入，θ1相当于单神经元的权值w。如果不包含θ0，那么则可能无法准确完成线性回归的功能。因此，对于单神经元结构而言，偏置值bias是必不可少的。
图1. 单神经元单变量输入与线性回归的对应模型
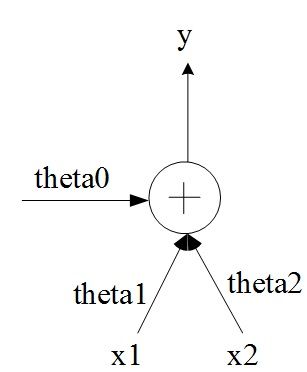
对于双变量线性回归模型：
而言，可实现双输入单神经元的功能。其偏置值对应θ0。
图2. 单神经元双变量输入与线性回归的对应模型
4. Matlab实现多变量梯度下降的线性回归
(1). 未进行归一化处理之前的matlab代码
两个输入变量x1和x2.
clear all
clc
% training sample data;
p0=6;
p1=7;
p2=2;
% the first group of inputs
x1=[7 9 12 5 4];
x2=[1 8 21 3 5];
% the second group of inputs
x1=[7 9 12 5 4 3];
x2=[1 8 21 3 5 26];
y=p0+p1*x1+p2*x2;
num_sample=size(y,2);
% gradient descending process
% initial values of parameters
theta0=9;
theta1=3;
theta2=9;
% theta0=19;theta1=23;theta2=91;
% theta0=0;theta1=0;theta2=0;
%learning rate
alpha=0.01; % good for the system with the first group of inputs
alpha=0.005; % good for the system the second group of inputs
% alpha=0.02; % bad for the system. the system will be unstable
% if alpha is too large, the final error will be much large.
% if alpha is too small, the convergence will be slow
epoch=10000;
for k=1:epoch
v_k=k
h_theta_x=theta0+theta1*x1+theta2*x2; % hypothesis function
Jcost(k)=((h_theta_x(1)-y(1))^2+(h_theta_x(2)-y(2))^2+(h_theta_x(3)-y(3))^2+(h_theta_x(4)-y(4))^2+(h_theta_x(5)-y(5))^2)/num_sample;
theta0=theta0-alpha*((h_theta_x(1)-y(1)) +(h_theta_x(2)-y(2)) +(h_theta_x(3)-y(3)) +(h_theta_x(4)-y(4)) +(h_theta_x(5)-y(5)))/num_sample;
theta1=theta1-alpha*((h_theta_x(1)-y(1))*x1(1)+(h_theta_x(2)-y(2))*x1(2)+(h_theta_x(3)-y(3))*x1(3)+(h_theta_x(4)-y(4))*x1(4)+(h_theta_x(5)-y(5))*x1(5))/num_sample;
theta2=theta2-alpha*((h_theta_x(1)-y(1))*x2(1)+(h_theta_x(2)-y(2))*x2(2)+(h_theta_x(3)-y(3))*x2(3)+(h_theta_x(4)-y(4))*x2(4)+(h_theta_x(5)-y(5))*x2(5))/num_sample;
% % disp('*********comp 1**************');
% r1=((h_theta_x(1)-y(1))+(h_theta_x(2)-y(2))+(h_theta_x(3)-y(3)));
% r2=sum(h_theta_x-y);
% % disp('*********comp 2**************');
% r3=((h_theta_x(1)-y(1))^2+(h_theta_x(2)-y(2))^2+(h_theta_x(3)-y(3))^2);
% r4=sum((h_theta_x-y).^2);
% % disp('*********comp 3**************');
% r5=((h_theta_x(1)-y(1))*x(1)+(h_theta_x(2)-y(2))*x(2)+(h_theta_x(3)-y(3))*x(3));
% r6=sum((h_theta_x-y).*x);
% if((r1~=r2)||(r3~=r4)||(r5~=r6))
% disp('***wrong result******')
% end
end
yt=theta0+theta1*x1+theta2*x2
plot(Jcost)
上述matlab代码中，当学习速率alpha小于等于0.01时，系统能收敛；但是，如果学习速率alpha越小，系统收敛的速度越慢。当学习速率alpha大于等于0.02时，系统发散，无法收敛。为了使得系统尽快收敛下一步采用归一化的方法来加速系统收敛。
(2). 对表达式进行简化后的matlab代码
clear all
clc
% training sample data;
p0=6;
p1=7;
p2=2;
x1=[7 9 12 5 4];
x2=[1 8 21 3 5];
y=p0+p1*x1+p2*x2;
num_sample=size(y,2);
% gradient descending process
% initial values of parameters
theta0=9;
theta1=3;
theta2=9;
% theta0=19;theta1=23;theta2=91;
% theta0=0;theta1=0;theta2=0;
%learning rate
alpha=0.005; % good for the system
alpha=0.01; % good for the system
% alpha=0.02; % bad for the system. the system will be unstable
% if alpha is too large, the final error will be much large.
% if alpha is too small, the convergence will be slow
epoch=10000;
for k=1:epoch
v_k=k
h_theta_x=theta0+theta1*x1+theta2*x2; % hypothesis function
Jcost(k)=sum((h_theta_x-y).^2)/num_sample;
r0=sum(h_theta_x-y);
theta0=theta0-alpha*r0/num_sample;
r1=sum((h_theta_x-y).*x1);
theta1=theta1-alpha*r1/num_sample;
r2=sum((h_theta_x-y).*x2);
theta2=theta2-alpha*r2/num_sample;
% Jcost(k)=((h_theta_x(1)-y(1))^2+(h_theta_x(2)-y(2))^2+(h_theta_x(3)-y(3))^2+(h_theta_x(4)-y(4))^2+(h_theta_x(5)-y(5))^2)/num_sample;
% theta1=theta1-alpha*((h_theta_x(1)-y(1))*x1(1)+(h_theta_x(2)-y(2))*x1(2)+(h_theta_x(3)-y(3))*x1(3)+(h_theta_x(4)-y(4))*x1(4)+(h_theta_x(5)-y(5))*x1(5))/num_sample;
% theta2=theta2-alpha*((h_theta_x(1)-y(1))*x2(1)+(h_theta_x(2)-y(2))*x2(2)+(h_theta_x(3)-y(3))*x2(3)+(h_theta_x(4)-y(4))*x2(4)+(h_theta_x(5)-y(5))*x2(5))/num_sample;
% % disp('*********comp 1**************');
% r1=((h_theta_x(1)-y(1))+(h_theta_x(2)-y(2))+(h_theta_x(3)-y(3)));
% r2=sum(h_theta_x-y);
% % disp('*********comp 2**************');
% r3=((h_theta_x(1)-y(1))^2+(h_theta_x(2)-y(2))^2+(h_theta_x(3)-y(3))^2);
% r4=sum((h_theta_x-y).^2);
% % disp('*********comp 3**************');
% r5=((h_theta_x(1)-y(1))*x(1)+(h_theta_x(2)-y(2))*x(2)+(h_theta_x(3)-y(3))*x(3));
% r6=sum((h_theta_x-y).*x);
% if((r1~=r2)||(r3~=r4)||(r5~=r6))
% disp('***wrong result******')
% end
end
yt=theta0+theta1*x1+theta2*x2
plot(Jcost)
(3). 进行归一化处理之后的matlab代码
clear all
clc
% training sample data;
p0=6;
p1=7;
p2=2;
x1=[7 9 12 5 4];
x2=[1 8 21 3 5];
x1_mean=mean(x1)
x1_max=max(x1)
x1_min=min(x1)
x2_mean=mean(x2)
x2_max=max(x2)
x2_min=min(x2)
x1=(x1-x1_mean)/(x1_max-x1_min)
x2=(x2-x2_mean)/(x2_max-x2_min)
% x1=[7 9 12 5 4 3];
% x2=[1 8 21 3 5 26];
y=p0+p1*x1+p2*x2;
num_sample=size(y,2);
% gradient descending process
% initial values of parameters
theta0=9;
theta1=3;
theta2=9;
% theta0=19;theta1=23;theta2=91;
% theta0=0;theta1=0;theta2=0;
%learning rate
alpha=1.9; % good for the system
% if alpha is too large, the final error will be much large.
% if alpha is too small, the convergence will be slow
epoch=300;
for k=1:epoch
v_k=k
h_theta_x=theta0+theta1*x1+theta2*x2; % hypothesis function
Jcost(k)=sum((h_theta_x-y).^2)/num_sample;
r0=sum(h_theta_x-y);
theta0=theta0-alpha*r0/num_sample;
r1=sum((h_theta_x-y).*x1);
theta1=theta1-alpha*r1/num_sample;
r2=sum((h_theta_x-y).*x2);
theta2=theta2-alpha*r2/num_sample;
end
yt=theta0+theta1*x1+theta2*x2
plot(Jcost)
(4). 进行归一化处理之后的matlab代码2
三个个输入变量x1、x2和x3.
clear all
clc
% training sample data;
p0=6;
p1=7;
p2=2;
p3=9;
x1=[7 9 12 5 4];
x2=[1 8 21 3 5];
x3=[3 2 11 4 8];
x1_mean=mean(x1)
x1_max=max(x1)
x1_min=min(x1)
x1=(x1-x1_mean)/(x1_max-x1_min)
x2_mean=mean(x2)
x2_max=max(x2)
x2_min=min(x2)
x2=(x2-x2_mean)/(x2_max-x2_min)
x3_mean=mean(x3)
x3_max=max(x3)
x3_min=min(x3)
x3=(x3-x3_mean)/(x3_max-x3_min)
y=p0+p1*x1+p2*x2+p3*x3;
num_sample=size(y,2);
% gradient descending process
% initial values of parameters
theta0=9;
theta1=3;
theta2=9;
theta3=2;
% theta0=19;theta1=23;theta2=91;
% theta0=0;theta1=0;theta2=0;
%learning rate
alpha=1.8; % good for the system
% alpha=0.01; % good for the system
% alpha=0.02; % bad for the system. the system will be unstable
% if alpha is too large, the final error will be much large.
% if alpha is too small, the convergence will be slow
epoch=2260;
for k=1:epoch
v_k=k
h_theta_x=theta0+theta1*x1+theta2*x2+theta3*x3; % hypothesis function
Jcost(k)=sum((h_theta_x-y).^2)/num_sample;
r0=sum(h_theta_x-y);
theta0=theta0-alpha*r0/num_sample;
r1=sum((h_theta_x-y).*x1);
theta1=theta1-alpha*r1/num_sample;
r2=sum((h_theta_x-y).*x2);
theta2=theta2-alpha*r2/num_sample;
r3=sum((h_theta_x-y).*x3);
theta3=theta3-alpha*r3/num_sample;
end
yt=theta0+theta1*x1+theta2*x2+theta3*x3
plot(Jcost)
(5). 结论
对输入值向量进行归一化处理之后，将学习速率从0.01提高到1.9,从而将获得系统收敛的epoch次数由10000次减少到300次。