opencv图片变形 仿射 旋转 透视 弯曲 鱼眼特效

1. 仿射变换

可将图片变换为平行四边形

/**@brief从三对对应点计算仿射变换。
@param src[] :原图上取三点坐标（三角形）
@param dst[] :目标三点坐标
@param return :返回2*3的变换矩阵
*/
CV_EXPORTS Mat getAffineTransform( const Point2f src[], const Point2f dst[] );


/ ** @brief对图像应用仿射变换。
函数warpAffine使用指定的矩阵转换源图像：
@param src输入图像。
@param dst输出图像，其大小为dsize，并且与src类型相同。
@param M \ f $ 2 \ times 3 \ f $转换矩阵。
@param dsize输出图像的大小。
@param标志插值方法( 详见 结构定义)
@param borderMode像素外推方法（ 详见 结构定义）
borderMode =＃BORDER_TRANSPARENT，表示目标图像中的像素对应于源图像中的“异常值”不会被该功能修改。
@param borderValue边界不变时使用的值；默认情况下为0。

@sa warpPerspective，调整大小，重新映射，getRectSubPix，转换
*/
CV_EXPORTS_W void warpAffine( InputArray src, OutputArray dst,
                              InputArray M, Size dsize,
                              int flags = INTER_LINEAR,
                              int borderMode = BORDER_CONSTANT,
                              const Scalar& borderValue = Scalar());

2. 旋转

/ ** @brief计算2D旋转的仿射矩阵。
@param center源图像中旋转的中心。
@param angle旋转角度，以度为单位。 正值表示逆时针旋转（坐标原点假定为左上角）。
@param scale各向同性比例因子。
@sa getAffineTransform，warpAffine，变换
* /
CV_EXPORTS_W Mat getRotationMatrix2D( Point2f center, double angle, double scale );

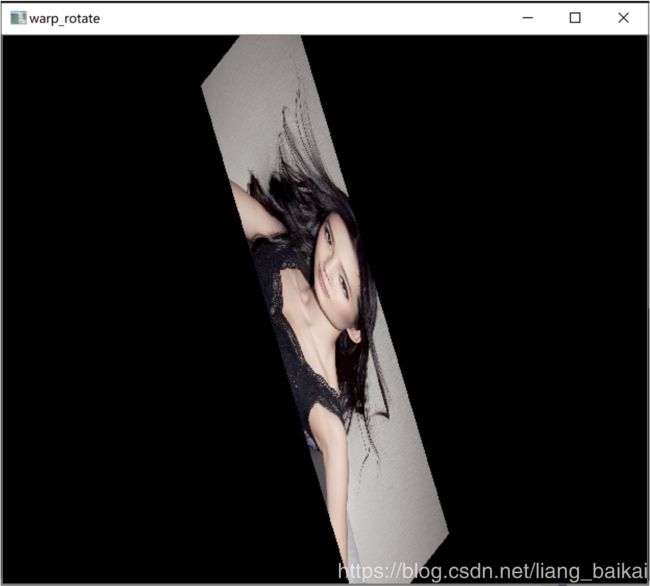
2.1 demo

int MPT_test_warpAffine(std::string file)
{
	Point2f srcTri[3];
	Point2f dstTri[3];
	Mat rot_mat(2, 3, CV_32FC1);
	Mat warp_mat(2, 3, CV_32FC1);
	Mat src, warp_dst, warp_rotate_dst;

	// 加载源图像
	src = imread(file, 1);
	// 设置目标图像的大小和类型与源图像一致
	warp_dst = Mat::zeros(src.rows, src.cols, src.type());
	// 设置源图像和目标图像上的三组点以计算仿射变换
	srcTri[0] = cv::Point2f(0, 0);
	srcTri[1] = cv::Point2f(src.cols - 1, 0);
	srcTri[2] = cv::Point2f(0, src.rows - 1);
	dstTri[0] = cv::Point2f(0, 0);
	dstTri[1] = cv::Point2f(src.cols - 1, src.rows * 0.5);
	dstTri[2] = cv::Point2f(0, src.rows * 0.5);

	// 求得仿射变换
	warp_mat = getAffineTransform(srcTri, dstTri);
	// 对源图像应用上面求得的仿射变换
	warpAffine(src, warp_dst, warp_mat, warp_dst.size());
	/** 对图像扭曲后再旋转 */
	// 计算绕图像中点顺时针旋转50度缩放因子为0.6的旋转矩阵
	Point center = Point(warp_dst.cols / 2, warp_dst.rows / 2);
	double angle = -50.0;
	double scale = 0.6;
	// 通过上面的旋转细节信息求得旋转矩阵
	rot_mat = getRotationMatrix2D(center, angle, scale);
	// 旋转已扭曲图像
	warpAffine(warp_dst, warp_rotate_dst, rot_mat, warp_dst.size());
	// 显示结果
	namedWindow("src", CV_WINDOW_NORMAL);
	namedWindow("warp", CV_WINDOW_NORMAL);
	namedWindow("warp_rotate", CV_WINDOW_NORMAL);
	imshow("src", src);
	imshow("warp", warp_dst);
	imshow("warp_rotate", warp_rotate_dst);
	waitKey(0);
	return 0;
}

3. 透视变换

可将矩形图片变换成梯形

根据4组点变换 返回3*3矩阵
CV_EXPORTS Mat getPerspectiveTransform( const Point2f src[], const Point2f dst[] );

/ ** @brief将透视转换应用于图像。
@param src输入图像。
@param dst输出图像，其大小为dsize，并且与src类型相同。
@param M \ f $ 3 \ times 3 \ f $转换矩阵。
@param dsize输出图像的大小。
@param标志插值方法
@param borderMode像素外推方法（#BORDER_CONSTANT或#BORDER_REPLICATE）。
@param borderValue边界不变时使用的值；默认情况下，它等于0。
@sa warpAffine，调整大小，重新映射，getRectSubPix，perspectiveTransform
* /
CV_EXPORTS_W void warpPerspective( InputArray src, OutputArray dst,
                                   InputArray M, Size dsize,
                                   int flags = INTER_LINEAR,
                                   int borderMode = BORDER_CONSTANT,
                                   const Scalar& borderValue = Scalar());

3.1 demo

int MPT_test_warpPerspective(std::string file)
{
	Point2f srcTri[4];
	Point2f dstTri[4];
	Mat warpPerspective_mat(3, 3, CV_32FC1);
	Mat src, warpPerspective_dst;

	// Load the image
	src = imread(file, IMREAD_COLOR);

	// Set the dst image the same type and size as src
	warpPerspective_dst = Mat::zeros(src.rows, src.cols, src.type());

	// 设置四组点，求出变换矩阵
	srcTri[0] = Point2f(0, 0);
	srcTri[1] = Point2f(src.cols - 1, 0);
	srcTri[2] = Point2f(0, src.rows - 1);
	srcTri[3] = Point2f(src.cols - 1, src.rows - 1);

	dstTri[0] = Point2f(0, src.rows * 0.13);
	dstTri[1] = Point2f(src.cols * 0.9, 0);
	dstTri[2] = Point2f(src.cols * 0.2, src.rows * 0.7);
	dstTri[3] = Point2f(src.cols * 0.8, src.rows);

	warpPerspective_mat = getPerspectiveTransform(srcTri, dstTri);

	//透视变换
	warpPerspective(src, warpPerspective_dst, warpPerspective_mat, src.size());

	namedWindow("src", 0);
	imshow("src", src);
	namedWindow("warpPerspective", 0);
	imshow("warpPerspective", warpPerspective_dst);
	waitKey(0);
	return 0;
}

4. 弯曲

4.1 S形状

int MPT_test_S_change(std::string file) {

	double RANGE = 1000;
	double PI = 3.1415926;
	Mat src = imread(file, IMREAD_COLOR);

	Mat dst(src.rows, src.cols, CV_8UC3, Scalar(0));
	for (int i = 0; i < dst.rows; i++) {
		double temp = (dst.cols - RANGE) / 2 + (dst.cols - RANGE) * sin((2 * PI * i) / dst.rows + PI) / 2;
		for (int j = int(temp + 0.5); j < RANGE + temp; j++) {
			int m = (int)((j - temp) * (src.cols) / RANGE);
			if (m >= src.cols)
				m = src.cols - 1;
			if (m < 0)
				m = 0;
			dst.at(i, j)[0] = src.at(i, m)[0];
			dst.at(i, j)[1] = src.at(i, m)[1];
			dst.at(i, j)[2] = src.at(i, m)[2];
		}
	}
	namedWindow("S形变形", CV_WINDOW_NORMAL);
	imshow("S形变形", dst);
	cv::waitKey(0);
	return 0;
}

4.2 波浪形

int MPT_test_2S_change(std::string file) {
	double RANGE = 100;
	double PI = 3.1415926;
	Mat src = imread(file, IMREAD_COLOR);
	Mat dst(src.rows, src.cols, CV_8UC3, Scalar(0));
	for (int j = 0; j < dst.cols; j++) {
		double temp = RANGE + RANGE * sin(j * PI * 2 / dst.cols);//利用sin函数得到一段正弦波，将图像映射到两个正弦波中即得到波浪形

		for (int i = int(temp); i < dst.rows + temp - 2 * RANGE; i++) {
			int m = (int)((i - temp) * (src.rows) / (dst.rows - RANGE));
			if (m >= src.rows)
				m = src.rows - 1;
			if (m < 0)
				m = 0;
			dst.at(i, j)[0] = src.at(m, j)[0];
			dst.at(i, j)[1] = src.at(m, j)[1];
			dst.at(i, j)[2] = src.at(m, j)[2];
		}
	}
	namedWindow("波浪变形", CV_WINDOW_NORMAL);
	imshow("波浪变形", dst);
	cv::waitKey(0);
	return 0;
}

5. 鱼眼特效

int MPT_test_fish_change(std::string file) {
	double PI = 3.1415926;
	Mat src = imread(file, IMREAD_COLOR);
	cv::resize(src, src, Size(1080, 1080));
	Mat dst(src.rows, src.cols, CV_8UC3, Scalar(0));

	for (int id = 0; id < dst.rows; id++) {
		for (int jd = 0; jd < dst.cols; jd++) {
			double xd = jd * 2.0 / dst.cols - 1.0;
			double yd = id * 2.0 / dst.cols - 1.0;
			double rd = sqrt(xd * xd + yd * yd);
			double phid = atan2(yd, xd);
			double xs = asin(rd) * 2 / PI * cos(phid);
			double ys = asin(rd) * 2 / PI * sin(phid);
			int is = round((ys + 1.0) * dst.rows / 2.0);
			int js = round((xs + 1.0) * dst.cols / 2.0);
			if (is > dst.rows || is < 0 || js>dst.cols || js < 0)
				continue;
			dst.at(id, jd)[0] = src.at(is, js)[0];
			dst.at(id, jd)[1] = src.at(is, js)[1];
			dst.at(id, jd)[2] = src.at(is, js)[2];
		}
	}
	cv::resize(dst, dst, Size(1080, 720));
	cv::namedWindow("鱼眼特效", CV_WINDOW_NORMAL);
	cv::imshow("鱼眼特效", dst);
	cv::imwrite("../image/fisheye.jpg", dst);
	cv::waitKey(0);
	return 0;
}

6. 结构定义

enum BorderTypes {
    BORDER_CONSTANT    = 0, //!< `iiiiii|abcdefgh|iiiiiii`  with some specified `i`
    BORDER_REPLICATE   = 1, //!< `aaaaaa|abcdefgh|hhhhhhh`
    BORDER_REFLECT     = 2, //!< `fedcba|abcdefgh|hgfedcb`
    BORDER_WRAP        = 3, //!< `cdefgh|abcdefgh|abcdefg`
    BORDER_REFLECT_101 = 4, //!< `gfedcb|abcdefgh|gfedcba`
    BORDER_TRANSPARENT = 5, //!< `uvwxyz|abcdefgh|ijklmno`

    BORDER_REFLECT101  = BORDER_REFLECT_101, //!< same as BORDER_REFLECT_101
    BORDER_DEFAULT     = BORDER_REFLECT_101, //!< same as BORDER_REFLECT_101
    BORDER_ISOLATED    = 16 //!< do not look outside of ROI
};

enum InterpolationFlags{
    /** nearest neighbor interpolation */
    INTER_NEAREST        = 0,
    /** bilinear interpolation */
    INTER_LINEAR         = 1,
    /** bicubic interpolation */
    INTER_CUBIC          = 2,
    /** resampling using pixel area relation. It may be a preferred method for image decimation, as
    it gives moire'-free results. But when the image is zoomed, it is similar to the INTER_NEAREST
    method. */
    INTER_AREA           = 3,
    /** Lanczos interpolation over 8x8 neighborhood */
    INTER_LANCZOS4       = 4,
    /** Bit exact bilinear interpolation */
    INTER_LINEAR_EXACT = 5,
    /** mask for interpolation codes */
    INTER_MAX            = 7,
    /** flag, fills all of the destination image pixels. If some of them correspond to outliers in the
    source image, they are set to zero */
    WARP_FILL_OUTLIERS   = 8,
    /** flag, inverse transformation

    For example, #linearPolar or #logPolar transforms:
    - flag is __not__ set: \f$dst( \rho , \phi ) = src(x,y)\f$
    - flag is set: \f$dst(x,y) = src( \rho , \phi )\f$
    */
    WARP_INVERSE_MAP     = 16
};

结构定义（中文）

enum InterpolationFlags {
    /**最近邻插值*/
    INTER_NEAREST = 0，
    /**双线性插值*/
    INTER_LINEAR = 1
    /**双三次插值*/
    INTER_CUBIC = 2
    /**使用像素面积关系重新采样。它可能是图像抽取的首选方法，因为它提供无云纹的结果。但是当图像放大时，它类似于INTER_NEAREST方法。 */
    INTER_AREA = 3，
    /**在8x8邻域上进行Lanczos插值*/
    INTER_LANCZOS4 = 4
    /**位精确双线性插值*/
    INTER_LINEAR_EXACT = 5
    /**内插代码的掩码*/
    INTER_MAX = 7
    /**标志，填充所有目标图像像素。如果其中一些对应于源图像，它们设置为零*/
    WARP_FILL_OUTLIERS = 8
    /** 标志，逆变换例如，#linearPolar或#logPolar转换为：-__not__标志未设置：\ f $ dst（\ rho，\ phi）= src（x，y）\ f $-设置了标志：\ f $ dst（x，y）= src（\ rho，\ phi）\ f $ */
    WARP_INVERSE_MAP = 16
};

参考文档

参考文档