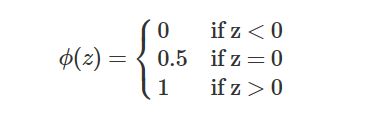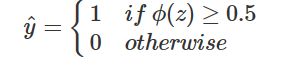银行流失用户分析及预测模型

自学的一个银行流失客户预警的小项目

0.引言-银行流失用户分析

银行客户流失是指银行的客户终止在该行的所有业务，并销号。但在实际运营中，对于具体业务部门，银行客户流失可以定位为特定的业务终止行为。

商业银行的客户流失较为严重，流失率可达20%。而获得新客的成本是维护老客户的5倍。因此，从海量客户交易数据中挖掘出对流失有影响的信息，建立高效的客户流失预警体系尤为重要。

客户流失的主要原因有：价格流失、产品流失、服务流失、市场流失、促销流失、技术流失、政治流失。有些时候表面上是价格导致的客户流失，但实际上多重因素共同作用导致了客户的流失。比如说，不现实的利润目标、价格结构的不合理、业务流程过于复杂、组织结构的不合理等等。

维护客户关系的基本方法：追踪制度，产品跟进，扩大销售，维护访问，机制维护。

因此建立量化模型，合理预测客群的流失风险是很有必要的。比如：常用的风险因子，客户持有的产品数量、种类，客户的年龄、性别，地理区域的影响，产品类别的影响，交易的时间间隔，促销的手段等等。根据这些因素及客户流失的历史数据对现有客户进行流失预测，针对不同的客群提供不同的维护手段，从而降低客户的流失率。

1. 数据初探索

1.1银行客户数据变量含义统计：

从业务水平上判定用户是否为流失客户

CUST_ID	用户ID
OPEN_ACC_DUR	开户时长
AGE	年龄
GENDER_CD	性别
HASNT_HOME_ADDRESS_INF	家庭住址
HASNT_MOBILE_TEL_NUM_INF	电话信息
LOCAL_CUR_SAV_SLOPE	本币活期储蓄波动率
LOCAL_CUR_MON_AVG_BAL	本币活期月均余额
LOCAL_CUR_MON_AVG_BAL_PROP	本币活期月均月占比
LOCAL_CUR_ACCT(account)_NUM	本币活期帐户数
LOCAL_OVEONEYR_FF_MON_AVG_BAL	本币一年以上整整季日均余额
LOCAL_FIX_MON_AVG_BAL	本币定期月均余额
LOCAL_FIX_MON_AVG_BAL_PROP	本币定期月均余额比例
LOCAL_BELONEYR_FF_SLOPE	本币一年以下整整波动率
LOCAL_BELONEYR_FF_MON_AVG_BAL	本币一年以下整整季日均余额
LOCAL_OVEONEYR_FF_SLOPE	本币一年以上整整波动率
LOCAL_SAV_SLOPE	本币存款波动率
LOCAL_SAV_CUR_ALL_BAL	本币活期存款总余额
LOCAL_SAV_MON_AVG_BAL	本币存款月均余额
SAV_SLOPE	存款波动率
SAV_CUR_ALL_BAL	活期存款总余额
SAV_MON_AVG_BAL	存款月均余额
FR_SAV_CUR_ALL_BAL
ASSET_CUR_ALL_BAL	活期资产总余额
ASSET_MON_AVG_BAL	资产月均余额
LOCAL_CUR_TRANS_TX_AMT	本币活期转账交易笔数
LOCAL_CUR_TRANS_TX_NUM	本币活期转账交易总数
LOCAL_CUR_LASTSAV_TX_AMT	本币活期续存交易金额
LOCAL_CUR_LASTSAV_TX_NUM	本币活期续存交易笔数
LOCAL_CUR_WITHDRAW_TX_AMT	本币活期存款金额
LOCAL_CUR_WITHDRAW_TX_NUM	本币活期存款笔数
LOCAL_FIX_OPEN_ACC_TX_NUM	本币定期开户交易笔数
LOCAL_FIX_OPEN_ACC_TX_AMT	本币定期开户交易金额
LOCAL_FIX_WITHDRAW_TX_NUM	本币定期存款交易笔数
LOCAL_FIX_WITHDRAW_TX_AMT	本币定期存款交易金额
LOCAL_FIX_CLOSE_ACC_TX_NUM	本币定期销户笔数
LOCAL_FIX_CLOSE_ACC_TX_AMT	本币定期销户总金额
L6M_INDFINA_ALL_TX_NUM	最近六个月个人理财总交易数目
L6M_INDFINA_ALL_TX_AMT	最近六个月个人理财总交易金额
POS_CONSUME_TX_AMT	客户POS财务类交易总金额
POS_CONSUME_TX_NUM	客户POS交易总数目
ATM_ACCT_TX_NUM	ATM交易总数目
ATM_ACCT_TX_AMT	AMT交易总金额
ATM_NOT_ACCT_TX_NUM	ATM非财务类交易数目
ATM_ALL_TX_NUM	ATM总交易数目
COUNTER_NOT_ACCT_TX_NUM	柜面非财务交易数目
COUNTER_ACCT_TX_AMT	柜面财务交易总金额
COUNTER_ACCT_TX_NUM	柜面财务交易总数目
COUNTER_ALL_TX_NUM	柜面总交易数目
NAT_DEBT_OPEN_ACC_DUR	国债开户时长
FINA_OPEN_ACC_DUR	委托理财开户时长
FUND_OPEN_ACC_DUR	代理基金开户时长
TELEBANK_ALL_TX_NUM	手机银行交易总数
CHURN_CUST_IND	流失客户

1.2数据统计性初探

1.2.1单因子分析

#导包（基于python3）：
import pandas as pd
import numbers
import numpy as np
import matplotlib.pyplot as plt
import random
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm#方差分析应用
from scipy.stats import chisquare
#读取数据：
bankChurn = pd.read_csv(r'/path/bankChurn.csv', header = 0)
externalData = pd.read_csv(r'/path/ExternalData.csv',header = 0)

#基于CUST_ID变量字段，连接两个表
AllData = pd.merge(bankChurn, externalData, on ='CUST_ID')

#构建数值型统计探索函数，其主要功能为作图描述各个变量的分布特性，确定离群值，函数输入参数如下：
def NumVarTracker(df, col, Target, filepath,):
    ‘‘‘
    :param df: the dataset containing numerical independent variable and dependent       variable样本集
    :param col: independent variable with numerical type变量
    :param target: dependent variable, class of 0-1目标
    :param filepath: the location where we save the histogram图片存储路径
    :param truncation: indication whether we need to do some truncation for outliers判断是否需要剔除离群值
    :return: the descriptive statistics
    ’’’

    #数据初步筛除空值（空值具有自己不与自己相等的属性）
    # extract target variable and specific indepedent variable
    validDf = df.loc[df[col] == df[col]][[col,target]]
	
    #统计非空值占比：
    validRcd = validDf.shape[0]*1.0/df.shape[0]
    validRcdFmt = "%.2f%%"%(validRcd*100)

    #数值型数据统计性描述：
    descStats = validDf[col].describe()
    mu = "%.2e" % descStats['mean']
    std = "%.2e" % descStats['std']
    maxVal = "%.2e" % descStats['max']
    minVal = "%.2e" % descStats['min']

    #各变量用户流失分布情况：
    x = validDf.loc[validDf[target]==1][col]
    y = validDf.loc[validDf[target]==0][col]
    xweights = 100.0 * np.ones_like(x) / x.size
    yweights = 100.0 * np.ones_like(y) / y.size

    #判断是否需要剔除离群值（离群值基于0.95分位点进行剔除）：
    if truncation == True:
        pcnt95 = np.percentile(validDf[col],95)
        x = x.map(lambda x: min(x,pcnt95))
        y = y.map(lambda x: min(x,pcnt95))

    #数据可视化探索数据：
    fig, ax = plt.subplots()
    ax.hist(x, weights=xweights, alpha=0.5,label='Attrition')#直方图
    ax.hist(y, weights=yweights, alpha=0.5,label='Retained')#直方图
    titleText = 'Histogram of '+ col +'\n'+'valid 
    pcnt ='+validRcdFmt+', Mean ='+mu+ ',  Std='+std+'\n max='+maxVal+', min='+minVal	
    #变量指标
    ax.set(title = titleText, ylabel = '% of Dataset in Bin')
    ax.margins(0.05)
    ax.set_ylim(bottom=0)
    plt.legend(loc='upper right')
    figSavePath = filepath+str(col)+'.png'
    plt.savefig(figSavePath)
    plt.close(1)#画图后图片不打开

 

可视化初步探索：

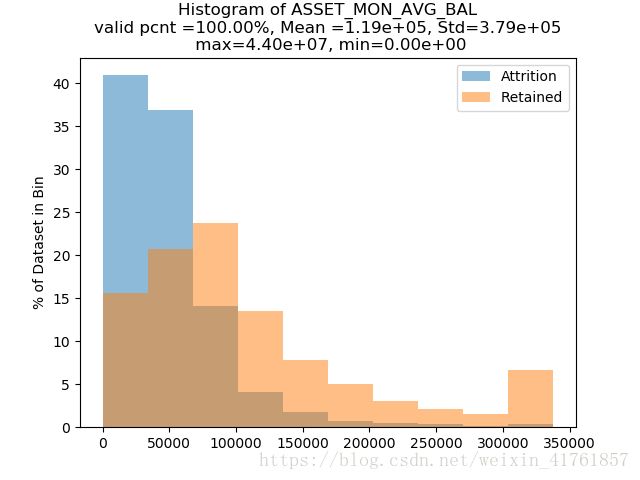
可视化图表判断某变量下，流失客户与非流失客户的分布情况，以ASSET_MON_AVG_BAL资产月均余额为例，该变量为行尾变量：

图1. 客户ASSET_MON_AVG_BAL变量下客户流失情况分布

可以看出，资产水平较低的客户流失率明显高于高资产水平客户的流失率。同时在图表上方可以看到该特征数据样本的缺失率，均值与标准差。

图2. 客户Age变量下客户流失情况分布

由图2，可以看出，低年龄客户的用户流失率更高。

这种分布类型的特征样本其方差过大，使得数据学习容易发生过拟合：

图3.本币活期转账交易金额变量下的客户流失情况分析

2）字符型变量数据

#数据与变量输入：
def CharVarPerf(df,col,target,filepath):
    '''
:param df: the dataset containing numerical independent variable and dependent variable
    :param col: independent variable with numerical type
    :param target: dependent variable, class of 0-1
    :param filepath: the location where we save the histogram
    :return: the descriptive statistics
'''
#初步筛除空值：
validDf = df.loc[df[col] == df[col]][[col, target]]
validRcd = validDf.shape[0]*1.0/df.shape[0]
recdNum = validDf.shape[0]
validRcdFmt = "%.2f%%"%(validRcd*100)

#统计类别变量的各个值的分布：
freqDict = {}
churnRateDict = {}
#for each category in the categorical variable, we count the percentage and churn rate（每个值的比例与对应的流失比例）
for v in set(validDf[col]):
#统计不同值的个数/collections的Counter函数可计算变量与变量的个数
vDf = validDf.loc[validDf[col] == v]
freqDict[v] = vDf.shape[0]*1.0/recdNum #Dataframe
churnRateDict[v] = sum(vDf[target])*1.0/vDf.shape[0]
descStats=pd.DataFrame({'percent':freqDict,'churnrate':churn RateDict})
fig = plt.figure()  # Create matplotlib figure
ax = fig.add_subplot(111)  # Create matplotlib axes子图
ax2 = ax.twinx()  # Create another axes that shares the same x-axis as ax.
plt.title('The percentage and churn rate for '+col+'\n valid pcnt ='+validRcdFmt)
descStats['churn rate'].plot(kind='line', color='red', ax=ax)
descStats.percent.plot(kind='bar', color='blue', ax=ax2, width=0.2,position = 1)
ax.set_ylabel('churn rate')
ax2.set_ylabel('percentage')
figSavePath = filepath+str(col)+'.png'
plt.savefig(figSavePath)
plt.close(1)

数据可视化结果讨论（举几个变量的例子）：

图5 客户买车比例与流失比例

对于新买车的用户的流失比例较低，而大多数的客户未向银行透露自己是否买车，而这部分客户流失比例较高。

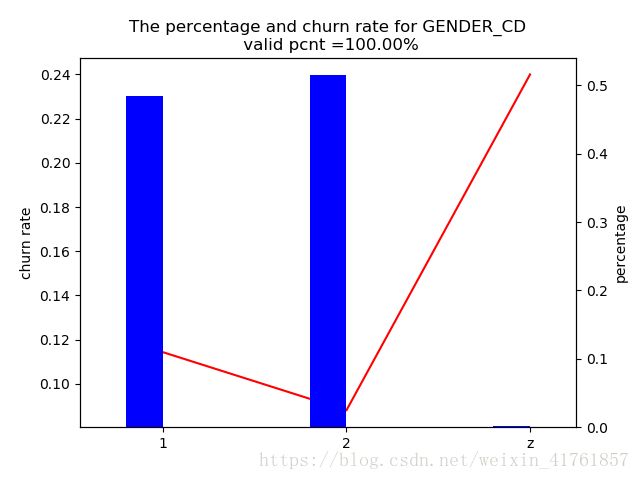
图6 性别与流失客户比例的关系

对于性别变量来说，男性客户2的用户流失比例小于男性客户1，而未知性别的客户对银行的信任度较低，其流失率也较高。

2.方差检验

利用方差检验方法，来探究类别变量对于结果是否有较为显著的影响。

        例如：检验ASSET_MON_AVG_BAL与CHURN_CUST_IND之间的差异性

anova_results=anova_lm(ols('ASSET_MON_AVG_BAL~CHURN_CUST_IND',AllData).fit())

print(anova_results)

PR值越小(越接近于0)，两组样本之间的差异性越小

 

1.2.2 多因子分析

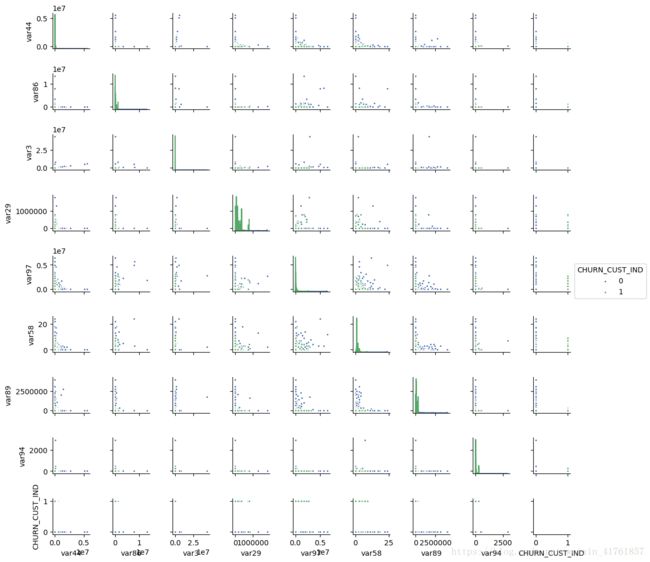
随机抽取8个变量探究变量两两间的关系

图4.随机抽取8个变量，探究两两之间关系

由图4可以看出，该图体现了两两变量之间的关系，及两个变量对预测结果的影响情况。本项目变量较多，且变量之间的关系较为复杂，有些变量对预测结果的可解释性影响较大。具体的特征工程还需要进一步的研究与讨论。如果两指标之间有较强的正相关或负相关的关系，则适当的删除冗余特征。

2. 数据预处理及指标去重

2.1数据预处理

        对于某些算法，例如lightgbm、xgboost算法，可以将数据空值作为类别或值进行预测，但有些算法无法根据空值进行训练，因此还需要进一步处理，对于缺失比例不大的数据可以应用均值或中值进行填充，如果数据缺失比例较大，应用回归填充或将空值作为一个统一的数值（结合具体的业务）进行填充。类别型变量预处理，则可根据最频繁模式与随机模型进行填补。其中较为特别的是将日期转化为开户持续时长duration：

import time

import datetime

#基准值获取，base为参考基准值

base2 = time.strptime(base,'%Y/%m/%d')

base3 = datetime.datetime(base2[0],base2[1],base2[2])

base4 = time.strptime(str(dateORI),'%m/%d/%Y')#日期字段匹配

date2 = datetime.datetime(base4[0],base4[1],base4[2])

daysGap = (date2-base3).days#得当前日期值与初始值之间的差值

 

2.2指标去重

1.指标合并

        将本币活期类与定期类指标相加，可以得到总指标（比如将本币活期余额与本币定期余额相加，得到的本币总余额）：

modelData['TOTAL_LOCAL_MON_AVG_BAL'] = modelData['LOCAL_CUR_MON_AVG_BAL','LOCAL_FIX_MON_AVG_BAL'].apply(sum, axis = 1)

       

2.比例计算

        由月均余额各类指标与年度指标相除，得到各个比例指标（Ratio）

3. 模型与参数调节

选择用GBDT进行预测，将所有特征样本输入训练模型会造成非常严重的过拟合，因此需要进行特征选择，

 

3.1特征选择（和降维的区别是什么？？？）

1.方差过滤法

        首先查看所有特征样本的方差：

        由于我想保留OPEN_ACC_DUR字段，因此设置方差过滤阈值为（阈值设定方法较为主观，可以基于具体的统计特征筛选方差/有些金额分布过于悬殊的值，可以设定阈值将其划分为几个等级）：100

       

from sklearn.feature_selection import VarianceThreshold
varianceThreshold = VarianceThreshold(threshold = 100)
varianceThreshold.fit_transform(modelData[allFeatures])
NumV=varianceThreshold.get_support()#大于阈值threshold的特征位置为True，否则为False

SeleFeatures = []#基于方差筛选特征
for i in range(len(NumV)):
    if NumV[i] == False:
        SeleFeatures.append(allFeatures[i])

2.相关系数法（皮尔逊）

        先计算各个特征对目标值的相关系数，选择更加相关的特征。

selectKBest = SelectKBest(f_regression,k=15)#找出与客户流失水平相关系数最大的15个特征找出来
selectKBest.fit_transform(modelData[SeleFeatures],modelData['CHURN_CUST_IND'])#在前十五范围内为True，不在为False
NumV2 = selectKBest.get_support()
print(NumV2)
SeleFeatures2 = []
for i in range(len(NumV2)):
    if NumV2[i] == True:
        SeleFeatures2.append(SeleFeatures[i])
print(len(SeleFeatures2))
print(SeleFeatures2)

 

3.卡方检验

检验变量对结果影响的显著性与否

检验性别是否对客户流失具有显著影响。

探究所筛选出的15个变量是否对客户流失具有显著影响

卡方检验值越大，拒绝假设的可能性越大

 

3.2模型选择

        GBDT的介绍：梯度提升决策树

        采用逻辑回归决策树CART Tree进行分类，应用梯度提升方法求解模型参数。

1. 逻辑回归

假设有一个二分类问题，输出为y∈{0,1}，而线性回归模型产生的预测值为z=wTx+b，z=wTx+b是实数值，我们希望有一个理想的阶跃函数来帮我们实现z值到0/1值的转化：

然而该函数不连续，我们希望有一个单调可微的函数来供我们使用，于是便找到了Sigmoid function来替代。

 

 

有了Sigmoid fuction之后，由于其取值在[0,1]，我们就可以将其视为类11的后验概率估计p(y=1|x)。说白了，就是如果有了一个测试点x，那么就可以用Sigmoid fuctionSigmoid fuction算出来的结果来当做该点x属于类别1的概率大小。于是，非常自然地，我们把Sigmoid fuction计算得到的值大于等于0.5的归为类别1，小于0.5的归为类别0。

2）梯度下降法

为确定逻辑回归中z的各参数，需要确定损失函数，使得损失函数最小的各w值。

        损失函数定义（由误差平方和结合最大似然估计法求得）为：(损失函数的选取各不相同)

        而利用梯度下降法，不断迭代求得最低点的wT，此时的wT即为使得损失函数最小的权重值。

        将样本输入即可得出判断目标结果所属的分类结果。

3.3参数调节

n_estimators：分类树的个数

learning rate：每个弱分类器的权重缩减系数v，也称之为步长。

Subsample:（不放回）抽样率，推荐在[0.5,0.8]之间，默认为1.0

init：即初始化的弱学习器，多用于对数据有先验知识，且在之前做过一定的拟合的时候

loss：算法的损失函数

max_features：划分时考虑的最大特征数

max_depth：决策树最大深度

min_samples_split：内部节点再划分所需的最小样本数，默认为2，样本量如果较大，则可以扩大该数。

min_simples_leaf: 叶子节点最少样本数

min_weight_fraction_leaf：叶子节点最小的样本权重

max_leaf_nodes：最大叶子节点数，通过限制最大叶子节点数，可以防止过拟合

min_impurity_split：节点划分最小不纯度

 

X_train,X_test,y_train,y_test = train_test_split(modelData[allFeatures2],modelData['CHURN_CUST_IND'],test_size = 0.3,random_state=9)
gbm0 = GradientBoostingClassifier(max_depth=1,random_state = 1)
gbm0.fit(X_train,y_train)
y_pred = gbm0.predict(X_test)
y_predprob = gbm0.predict_proba(X_test)[:,1]

#参数调节过程：
### tunning max_features
param_test4 = {'max_features':range(5,31,2)}
gsearch4 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, n_estimators=70,max_depth=9, min_samples_leaf =70,min_samples_split =500, subsample=0.8, random_state=10), param_grid = param_test4, scoring='roc_auc',iid=False, cv=5)
gsearch4.fit(X_train,y_train)
gsearch4.grid_scores_, gsearch4.best_params_, gsearch4.best_score_

## tunning subsample
param_test5 = {'subsample':[0.6,0.7,0.75,0.8,0.85,0.9]}
gsearch5 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.1, n_estimators=70,max_depth=9, min_samples_leaf =70, min_samples_split =500, max_features=28, random_state=10), param_grid = param_test5, scoring='roc_auc',iid=False, cv=5)
gsearch5.fit(X_train,y_train)
gsearch5.grid_scores_, gsearch5.best_params_, gsearch5.best_score_

# tunning the learning rate
gbm2 = GridSearchCV(estimator = GradientBoostingClassifier(learning_rate=0.05, n_estimators=70,max_depth=9, min_samples_leaf =70, min_samples_split =1000, max_features=28, random_state=10,subsample=0.8), param_grid = param_test5, scoring='roc_auc',iid=False, cv=5)
gbm2.fit(X_train,y_train)

 

针对具体的业务问题，关键在于迭代更新方案（不断优化泛化性能），发现数据的新的特性，最终设计出合适于具体业务的模型。