对抗变分贝叶斯：变分自编码器与生成对抗网络的统一（三）

       在之前的两篇博文中都是讲的如何利用pytorch进行AVB的代码实践，而关于论文的翻译则在这篇博文中进行。全文皆是译者人工翻译，如有不恰当或不正确的地方还请及时指出。

对抗变分贝叶斯：变分自编码器与生成对抗网络的统一

摘要

       变分自编码器是一类具有显式隐变量的模型，可以学习训练数据的复杂的概率分布。但是VAE模型的质量却非常依赖于推断模型的显式表现力。本文提出了对抗变分自编码器——一种可以用具有任意显式表现力的推断模型训练变分自编码器的技术。我们通过引入一个辅助的判别网络将最大似然问题重新描述成一个二人博弈游戏，从而有原则地结合了VAE与GAN。文中展示了在非参数限制中我们的方法可以完成一个对于生成模型参数精确的最大似然分布，以及对于给定观测的隐变量的精确后验分布。与结合VAE与GAN的很多有竞争力的模型相反的是，我们的方法具有一套清晰的理论依据，此外还保留了标准VAE的大多数优点并且易于实现。

1、介绍

       在机器学习中，生成模型是一类可以用无标签的数据集训练并在训练完成后可以生成新的数据点的模型。因为生成新内容需要对已有训练数据很好的理解，因此这类模型通常也被视为无监督学习的关键因素。
       近几年来，生成模型效果越来越好，已经有很多模型诸如Pixel-RNNs、Pixel-CNNs、real NVP、Plug&Play 生成模型被提出和研究，其中两个最重要的生成模型就是VAEs和GANs。
       VAEs和GANs各有各的优缺点：在学习自然图像的表达时，GAN通常生成视觉上轮廓清晰的图像，VAE可以产生生成模型和推断模型，并据研究称，VAE通常带来更好的对数似然。进来被提出的BiGANs就是给GANs添加了一个推断模型，然而可以看到它的重建结果也只是模糊地近似与输入，并且通常是在语义上而非像素值上近似。
       VAEs不能生成清晰图像的原因通常被认为是训练过程中的推断模型不能足够显式有表现力地捕捉到真实后验分布。的确，最近有工作表明使用更显式具有表现力的模型基本上可以在视觉上以及对数似然界上带来更好的结果。最近也有工作表明一个高度显式表现力很强的推断模型对于一个强有力的解码器是十分必要的，它允许模型更完全地利用隐空间。
       在这篇文章中，我们提出了对抗变分贝叶斯，一种可以用任意灵活的由神经网络参数化的推断模型训练变分自编码器的技术。我们展示了在非参数限制中我们可以得到关于生成模型的最大似然分布以及正确的后验分布。
       此前也存在着结合VAEs和GANs的一些尝试，但是大多数尝试都不是从最大似然角度出发的，因此通常不会产生最大似然分布。举例来说，在对抗自编码器AAE中，VAE训练目标函数中的KL散度正则化项被替换成了对抗损失，用来鼓励总的后验分布接近于隐变量的先验分布。尽管如此，AAE仍然不能最大化最大似然目标函数的下界，我们在6.2节中展示了AAE可以被解释成我们的方法的一种近似，从而建立起AAEs与最大似然学习的关系。
       在生成模型的介绍之外，AVB产生了一种用神经采样器实现变分贝叶斯的新方法。如图1阐述，我们用AVB训练神经网络去从复杂的非标准化的概率分布中采样，这可以导致对于概率模型后验分布精确的近似，例如进行贝叶斯参数估计。我们所想到的唯一可以处理这种显式具有表现力的推断模型的其他变分方法是基于Stein Discrepancy的。然而，这些方法通常并不能直接作用于逆KL散度，因此不能被用来在学习隐变量模型时近似变分下界。

图1：我们提出了一种可以允许神经采样器在变分贝叶斯中难于处理的概率密度进行采样、并且作为推断模型可以学习隐变量模型的方法。这个实验样例展示了我们的方法能够精确地近似复杂的后验分布，就像右面展示的那样。

       我们的贡献如下所示：
       （1）我们使得任意灵活的推断模型用于对抗训练变分自编码器变得可能；
       （2）我们给出了我们方法的理论推导，表明在非参数限制中我们的方法可以恢复真实的后验分布以及生成模型参数的真实的最大似然分布；
       （3）我们用实验阐述了我们的模型可以学习到丰富的后验分布并且对于复杂的数据集可以产生非常好的样本。

2、背景

       因为我们的模型是VAE的扩展，因此我们开始简要回顾一下VAEs。
       VAE是一种参数化的生成模型，可被阐述为一个给定隐变量后观测变量的分布$p_{\theta }(x|z)$，一个关于隐变量的先验分布$p(z)$，以及一个给定观测变量关于隐变量的近似推断模型$q_{\varphi }(z|x)$。可以证明：
$$\log p_{\theta }(x)\ge -\mathrm{K}\mathrm{L}(q_{\varphi }(z|x),p(z))+{\mathrm{E}}_{q_{\varphi }(z|x)}\log p_{\theta }(x|z).（2.1）$$
上式中等号右边的式子叫做变分下界或者ELBO，如果$\varphi$满足$q_{\varphi }(z|x)=p_{\theta }(x|z)$，我们可以得到：
$$\log p_{\theta }(x)=\underset{\varphi }{\max }-\mathrm{K}\mathrm{L}(q_{\varphi }(z|x),p(z))+{\mathrm{E}}_{q_{\varphi }(z|x)}\log p_{\theta }(x|z).（2.2）$$
然而，一般来说这种情况是不存在的，因此我们只能得到一个不等式。
       当实现最大似然训练时，我们的目标是优化边缘对数似然：
$${\mathrm{E}}_{p_{D(x)}}\log p_{\theta }(x).（2.3）$$
上式中的$p_D$是数据分布。不幸的是，关于$\log p_{\theta }(x)$的计算需要从$p_{\theta }(x,z)$中把$z$边缘化出来，这通常是难以实现的。变分贝叶斯采用不等式（2.1）将难以处理的优化问题（2.3）改写为：
$$\underset{\theta }{\max }\underset{\varphi }{\max }[-\mathrm{K}\mathrm{L}(q_{\varphi }(z|x),p(z))+{\mathrm{E}}_{q_{\varphi }(z|x)}\log p_{\theta }(x|z)].(2.4)$$
根据不等式（2.1），我们仍然可以优化真实最大似然目标函数（2.3）。
       自然可以看出，这个下界的质量取决于推断模型$q_{\varphi }(z|x)$的显式表现力。通常来说，$q_{\varphi }(z|x)$取作一个带有对角协方差矩阵的高斯分布，它的均值和方差向量被输入$x$的神经网络参数化。虽然这个模型关于$x$的取值非常灵活，但它关于$z$的取值非常受限，这潜在地限制了得到的生成模型的质量。事实上，可以观察到对自然图像应用标准的VAE通常会得到模糊的生成图像。

3、方法

       在这个部分我们将展示如何用一个黑箱推断模型$q_{\varphi }(z|x)$并采用对抗训练来获得一个关于$\theta$的近似最大似然分布${\theta }^{\ast }$以及关于真实后验分布$p_{\theta }(z|x)$的近似估计$q_{{\varphi }^{\ast }}(z|x)$。这在图2中进行了可视化：左边展示的是VAE的经典结构，右边展示的是我们灵活的黑箱推断模型。与应用高斯推断模型的VAE恰好相反，我们将噪声${ϵ}_1$作为推断模型额外的输入而不是将它添加在末尾，这样可以使推断网络学习更为复杂的概率分布。

图2：标准VAE与带有黑箱推断模型VAE的结构上的对比，其中${ϵ}_1$和${ϵ}_2$表示从某个噪声分布中采样的噪声。虽然对于变分自编码器来说可能存在更复杂的推断模型，通常它们都不如我们的黑箱方法灵活。

3.1、推导

       为了推导我们的方法，我们将（2.4）的优化问题重新写为：
$$\underset{\theta }{\max }\underset{\varphi }{\max }{\mathrm{E}}_{p_{D(x)}}{\mathrm{E}}_{q_{\varphi }(z|x)}(\log p(z)-\log q_{\varphi }(z|x)+\log p_{\theta }(x|z)).(3.1)$$
当我们有了一个精确的关于$q_{\varphi }(z|x)$的表达比如被神经网络参数化的高斯分布时，式（3.1）可以用重参数技巧和随机梯度下降方法进行优化。不幸的是，这种情况不适用于我们定义$q_{\varphi }(z|x)$为一个如图2b所示的黑箱过程。
       我们的想法是通过隐式地将
$$\log p(z)-\log q_{\varphi }(z|x).(3.2)$$
项表达为上述我们引出的问题中的一个额外的实值判别网络$T(x,z)$的优化值，来绕过这个问题。
       更具体地讲，考虑对于一个给定$q_{\varphi }(z|x)$的判别器$T(x,z)$的下列目标函数：
$$\underset{T}{\max }{\mathrm{E}}_{p_{D(x)}}{\mathrm{E}}_{q_{\varphi }(z|x)}\log \sigma (T(x,z))+{\mathrm{E}}_{p_{D(x)}}{\mathrm{E}}_{p(z)}\log (1-\sigma (T(x,z))).(3.3)$$
其中，$\sigma (t):=(1+e^{-t}{)}^{-1}$表示Sigmoid函数。直觉上，$T(x,z)$尽力地从目前的推断模型如$p_D(x)q_{\varphi }(z|x)$采样得到的$(x,z)$对中区分出从$p_D(x)p(z)$分布中独立采样得到的$(x,z)$对。
       为了简化理论分析，我们假设$T(x,z)$模型足够灵活可以代表任意关于$x$、$z$两个变量的函数，这个假设通常被引用为非参数限制并且可以由深度神经网络是广泛函数估计器的事实证明。
于是，根据目标函数（3.3）得到的最优判别器$T^{\ast }(x,z)$就被表示为式（3.2）中的负数项。

命题1、

       对于固定的$p_{\theta }(x|z)$以及$q_{\varphi }(z|x)$，根据（3.3）中的目标函数得到的最优判别器$T^{\ast }$可以写为：
$$T^{\ast }(x,z)=\log q_{\varphi }(z|x)-\log p(z).(3.4)$$
证明：
       证明细节类似于Goodfellow et al. (2014).文章中命题1的证明。
命题1与式（3.1）一起，允许我们将（2.4）中的优化目标重新写为：
$$\underset{\theta ,\varphi }{\max }{\mathrm{E}}_{p_{D(x)}}{\mathrm{E}}_{q_{\varphi }(z|x)}(-T^{\ast }(x,z)+\log p_{\theta }(x|z)).(3.5)$$
其中$T^{\ast }(x,z)$定义为最大化（3.3）的函数。
       为了优化（3.5），我们需要计算（3.5）的关于$\theta$和$\varphi$的梯度。虽然关于$\theta$梯度的推导很直接，但关于$\varphi$梯度的推导很复杂，因为我们已经间接地定义了$T^{\ast }(x,z)$作为辅助优化问题的解，而这个优化问题本身又取决于$\varphi$。但是，下述命题展示了对于$T^{\ast }(x,z)$中显式出现的$\varphi$的梯度推导不是必要的：

命题2、

       我们可以得到：
$${\mathrm{E}}_{q_{\varphi }(z|x)}({\nabla }_{\varphi }{T}^{\ast }(x,z))=0.(3.6)$$
对于一个合适的函数$z_{\varphi }(x,ϵ)$，采用重参数化技巧可以将（3.5）重新写为以下形式：
$$\underset{\theta ,\varphi }{\max }{\mathrm{E}}_{p_{D(x)}}{\mathrm{E}}_{ϵ}(-T^{\ast }(x,z_{\varphi }(x,ϵ))+\log p_{\theta }(x|z_{\varphi }(x,ϵ))).(3.7)$$
式（3.7）与命题1一起，允许我们推导关于$\theta$和$\varphi$的梯度的无偏估计。

3.2、算法

       理论上，命题1和命题2允许我们直接对（2.4）中的目标函数使用随机梯度下降方法。然而，这需要保证计算复杂的$T^{\ast }(x,z)$是最优的。因此，我们将（3.3）和（3.7）中的优化问题视为二人博弈游戏，命题1和命题2说明了这场博弈中的纳什平衡产生了（2.4）中目标函数的稳定点。
       实践上，我们尝试了对式子（3.3）和（3.7）采用带有不同步长$h_i$的SGD方法寻找纳什平衡，参考算法1。这里，我们用一个向量$\psi$将神经网络$T$重参数化。即使我们无法保证这个算法收敛，这个算法的任何稳定点都会产生（2.4）中目标函数的一个稳定点。


       注意，固定$\theta$和$T$优化（3.5）中的$\varphi$会使编码器网络坍塌到一个确定的函数，这也是对于常规GANs普遍存在的问题。因此，在优化（3.5）时，很有必要保证判别器$T$网络接近于最优值。因此，算法1的一个变体对对抗模型实施多次SGD更新，而对生成模型实施一次SGD更新。然而，除非另有说明，我们在实验中采用了简化的AVB的单步更新版本。

3.2、理论结果

       在3.1节中我们对（2.4）中的变分下界采用SGD推导了 AVB。在这一小节中，我们将从博弈论的角度分析算法1的一些特性。
如下列命题所示，算法1的全局纳什平衡产生了（2.4）目标函数的全局最优：

命题3、

       假设$T$可以代表有关两个变量的任意函数，若定义$({\theta }^{\ast },{\varphi }^{\ast },T^{\ast })$为（3.3）和（3.7）二者博弈的纳什平衡，则有：$$T^{\ast }(x,z)=\log q_{{\varphi }^{\ast }}(z|x)-\log p(z).(3.8)$$并且$({\theta }^{\ast },{\varphi }^{\ast })$是（2.4）中变分下界的全局最优。
       我们将$q_{\varphi }(z|x)$重参数化为一个神经网络的操作使得$q_{\varphi }(z|x)$可以代表隐空间的几乎任意一个概率密度函数，这也就产生了下列推论：

推论4、

       假设$T$可以代表有关两个变量的任意函数、$q_{\varphi }(z|x)$可以代表隐空间的任意一个概率密度函数，若定义$({\theta }^{\ast },{\varphi }^{\ast },T^{\ast })$为（3.3）和（3.7）二者博弈的纳什平衡，则有：
       （1）${\theta }^{\ast }$是最大似然分布；
       （2）$q_{{\varphi }^{\ast }}(z|x)$等于真实后验分布$p_{{\varphi }^{\ast }}(z|x)$；
       （3）$T^{\ast }$是$x$和$z$之间的点互信息（PMI），即：$$T^{\ast }(x,z)=\log \frac{p_{{\theta }^{\ast }}(x,z)}{p_{{\theta }^{\ast }}(x)p(z)}.(3.9)$$
证明：
       这是命题3的直接结果，因为在这种情况下如果（1）和（2）成立，那么$({\theta }^{\ast },{\varphi }^{\ast })$可以最优化（2.4）中的变分下界，将（2）中的结果代入到式（3.8）中即可得到（3）。

4、自适应对比度

       尽管在非参数限制中我们的方法可以产生正确的结果，但是在实践中$T(x,z)$可能不能足够接近最优的函数$T^{\ast }(x,z)$。这个问题的原因在于，AVB计算两个密度$p_D(x)q_{\varphi }(z|x)$和$p_D(x)p(z)$的对比度，而这两个密度往往是非常不同的。然而，众所周知，在对比两个非常相似的密度时，对于似然比估计，采用逻辑回归的方法可以得到不错的结果。
       为了提升估计的质量，我们由此提出了一个辅助的条件概率分布$r_{\alpha }(z|x)$，其密度已知，用来近似$q_{\varphi }(z|x)$。举个例子，$r_{\alpha }(z|x)$可以是带有对角协方差矩阵的高斯分布，其均值和方法与$q_{\varphi }(z|x)$的均值和方差相匹配。
       有了这个辅助的分布，我们可以将（2.4）中的变分下界重新写为：
$${\mathrm{E}}_{p_{D(x)}}[-\mathrm{K}\mathrm{L}(q_{\varphi }(z|x),r_{\alpha }(z|x))+{\mathrm{E}}_{q_{\varphi }(z|x)}(-\log r_{\alpha }(z|x)+\log p_{\varphi }(x,z))].(4.1)$$
       我们知道式（4.1）中的第二项的$r_{\alpha }(z|x)$适用于关于$\theta$和$\varphi$的SGD，然而，我们可以像第3节所述的那样用AVB估计第一项。如果$r_{\alpha }(z|x)$能很好地近似$q_{\varphi }(z|x)$，二者之间的KL散度$\mathrm{K}\mathrm{L}(q_{\varphi }(z|x),r_{\alpha }(z|x))$通常会比$\mathrm{K}\mathrm{L}(q_{\varphi }(z|x),p(z))$小很多，这使得对抗网络更容易地学到正确的概率比。
       我们称这种技术为自适应对比度（AC），因此我们现在正在将当前的推断网络$q_{\varphi }(z|x)$与一个自适应的分布$r_{\alpha }(z|x)$对比而不是与先验分布$p(z)$对比。采用自适应对比度，生成模型$p_{\theta }(x|z)$和推断模型$q_{\varphi }(z|x)$就可以由最大化下面的式子来进行训练：
$${\mathrm{E}}_{p_{D(x)}}{\mathrm{E}}_{q_{\varphi }(z|x)}(-T^{\ast }(x,z)-\log r_{\alpha }(z|x)+\log p_{\theta }(x|z)).(4.2)$$
其中，$T^{\ast }(x,z)$是能区分从$r_{\alpha }(z|x)$和$q_{\varphi }(z|x)$采样的样本的最优判别器。
       考虑到现在是这样一种情况：$r_{\alpha }(z|x)$是带有对角协方差矩阵的高斯分布，其均值和方法与$q_{\varphi }(z|x)$的均值和方差相匹配。因为在重参数化时KL散度是不变的，（4.1）中的第一项可以被重新写为：
$${\mathrm{E}}_{p_{D(x)}}\mathrm{K}\mathrm{L}({\tilde{q}}_{\varphi }(\tilde{z}|x),r_0(\tilde{z})).(4.3)$$
其中，${\tilde{q}}_{\varphi }(\tilde{z}|x)$表示标准化后的向量的分布$\tilde{z}:=\frac{z-\mu (x)}{\sigma (x)}$，$r_0(\tilde{z})$是均值为0、方差为1的高斯分布。此时，对抗网络只会影响从高斯分布产生$q_{\varphi }(z|x)$的偏差，而对它的位置与尺度无影响。
       实践中，我们采用了蒙特卡罗(MC)估计$\mu (x)$和$\sigma (x)$。

5、实验

       我们既在变分推断中作为一种黑箱方法，又在生成模型的学习中测试了我们的方法。前者的应用对应于我们固定生成模型和一个数据点$x$，希望学习后验分布$q_{\varphi }(z|x)$的情况。

5.1、变分推断

       当生成模型和数据点$x$固定时，AVB为带有任意复杂近似分布的变分贝叶斯提供了一种新的技术。我们将这个技术应用到 Gelman et al. (2014)书中的 “Eight School” 例子（这里译者给出例子的一个链接：https://docs.pymc.io/notebooks/Diagnosing_biased_Inference_with_Divergences.html#The-Eight-Schools-Model）。在这个例子中，八个学校的训练效果$y_i,i=1,...,8$被建模为：
$$y_i\sim \mathcal{N}(\mu +\theta \cdot {\eta }_i,{\sigma }_i),$$
其中，$\mu$，$\tau$和参数${\eta }_i$是需要推断的模型参数。我们给予模型参数一个$\mathcal{N}(0,1)$的先验，并将AVB与STAN中实施的带有高斯推断模型的两种变分方法进行比较。我们使用一个简单的两层模型作为后验以及一个强有力的带有残差模块的5层网络作为判别器。对于每个后验更新迭代，我们对对抗者实施了两步更新。真实的数据由采用STAN运行500000次HMC（Hamiltonian蒙特卡罗）得到。注意，AVB和作为基准的变分方法允许在训练后绘制任意数量的样本，但是HMC只能产生固定数量的样本。
       我们对来自真实数据的10000个样本应用ITE包（Szabo, 2013）以及相应的近似方法估计KL散度来评估所有这些方法。不同方法随着迭代次数的变化得到的KL散度在图3中画出。可以看到，我们的方法性能明显地优于带有高斯推断模型的方法。为了定性化可视化，我们也对2维的$(\mu ,\tau )-$和$(\tau ,{\eta }_1)-$变量应用了核密度估计，正如图4所示。与带有高斯推断模型的变分贝叶斯相反的是，我们的方法清晰地捕捉了后验分布的多模态。我们也观察到，自适应对比度（AC）可以使模型的学习更加鲁棒，并且可以提高所得模型的质量。

图3：与从Hamiltonian蒙特卡罗（HMC）方法得到的真实后验的KL散度的对比。

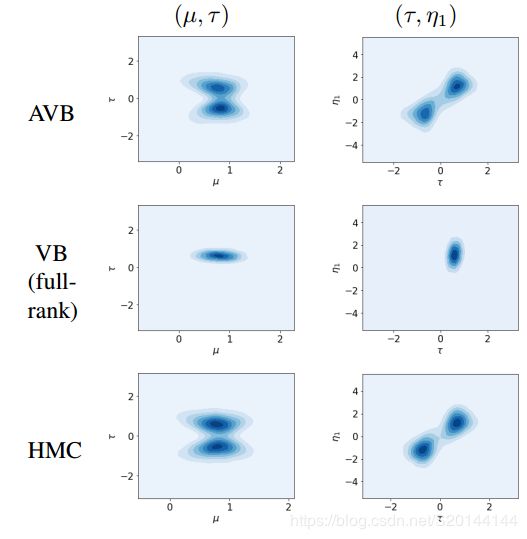
图4：通过查看10维后验的近似的两个边缘分布对比“Eight Schools”例子中的AVB与VB。可以看到，AVB准确地捕捉到后验分布的多模态；与之相反，VB仅仅关注于单个模态，由HMC方法得到的真实值已在最后一行给出。

5.2、生成模型

合成例子

       为了阐述我们的方法在学习生成模型时的应用，我们在一个只包含了如图5所示的2×2二值图像空间的4个数据点的简单的合成数据集和一个2维的隐空间上训练了神经网络，编码器和解码器都被每层512个神经元的2层全连接的神经网络参数化。编码器网络输入一个数据点$x$和一个高斯随机噪声向量$ϵ$，产生一个隐编码$z$；解码器网络输入一个隐编码$z$，产生四个独立的伯努利分布的参数，每个对应于输出图像的一个像素。对抗器部分被两个每层512神经元的两层神经网络参数化，两个网络分别作用于$x$和$z$，其512维的输出用内积方式结合起来。

图5：合成数据集中的训练样本。

       我们将我们的方法与带有对角高斯后验分布的变分自编码器进行比较。后者的编码器和解码器也按照上述方式参数化，但是编码器不将噪声$ϵ$作为输入，并且编码器产生的是均值向量和方差向量，而非单个样本。
       我们在图6中将隐空间所学到的划分进行可视化，其中每种颜色对应于$x-$隐空间的一种状态。尽管变分自编码器将隐空间划分成4个高斯的混合，但对抗变分自编码器学习到一个更复杂的后验分布。这个可以通过计算先验$p(z)$和总计的后验$q_{\varphi }(z):=\int q_{\varphi }(z|x)p_D(x)\mathrm{d}x$的KL散度来量化，这里我们采用了ITE-包 (Szabo, 2013)估计，参考表格1。注意图6中不同颜色的区别完全是由于推断模型中的噪声$ϵ$。

图6：在合成数据集上训练的VAE与AVB的隐编码分布。

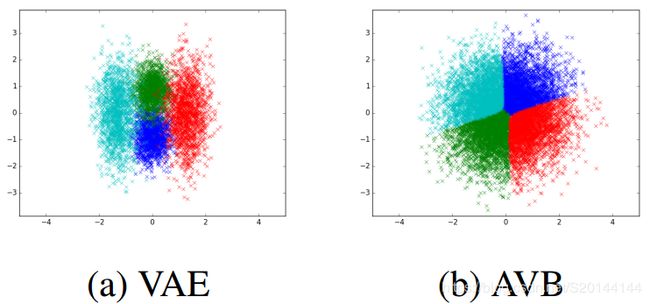
       AVB能学习到更为复杂的后验模型的能力导致了表格1所示的提升的性能。特别地，与标准VB相比，AVB能带来更高的与$-\mathrm{l}\mathrm{o}\mathrm{g}(4)$最优值接近的似然度，因为VB不能适当地划分隐空间。另外，可以看到当采用AVB而标准带有对角高斯推断模型的VB时，由输入$x$与采用编码器解码器网络得到的它的重构之间的平均交叉熵定义的重构误差也会更小。我们也可以观察到，估计的变分下界接近于真实的对数似然，说明对抗器已经学到了正确的函数。

表1：合成数据集上VAE与AVB的对比。

MNIST数据集

       此外，我们还基于DCGAN结构在二值化的MNIST数据集上训练了深度卷积网络。对于解码器网络，我们采用了5层深度卷积神经网络；对于编码器网络，我们采用了一个允许高效计算$q_{\varphi }(z|x)$时刻值的网络结构。想法是定义编码器为一个学到的基础噪声向量的线性组合，其中每个噪声向量由一个小型的全连接网络参数化，不同噪声组合的系数由一个作用于$x$的神经网络参数化。对于对抗器，我们将作用于$x$和$z$的全连接网络替换为每层1014个神经元的4层全连接网络。我们还给末尾的结果单独地加入了神经网络作用于$x$和$z$的结果。
       为了验证我们的方法，我们运行了Annealed Importance Sampling (AIS) (Neal, 2001)，一个用于验证基于生成模型解码器的黄金准则，带有在2048个测试样本上的1000个中间分布和5条并行链，结果在表格2中报道。采用了AIS，可以看到不带有AC的AVB将真实的ELBO估计过高，这降低了它的性能。尽管结果表明带有AC的AVB也会在高维情况下高估真实的ELBO，我们注意到由AIS计算得到的对数似然估计也只是真实对数似然的一个下界。

表2：在MNIST数据集上AVB以及其他提升VAE性能方法的对数似然。可以看到我们的方法在二值化的MNIST数据集上获得了最高的对数似然值。表格下半部分的近似的对数似然值是由重要性采样而非AIS方法得到的。

       可以看到，采用带有AC的AVB可以提升标准VAE以及不带有AC的AVB的性能。当与目前最先进的方法进行对比时，可以看到我们的方法在二值MNIST数据集上得到最好的结果。一些MNIST的随机样本已在图7中给出，可以看到我们的模型可以产生与训练数据集在感知上接近的随机样本。

图7：MNIST数据集训练的模型独立采样的样本。

6、相关工作

6.1、AVB与VAE的关系

       AVB与标准VAE的优化目标相同，但是在近似KL散度时采用的是对抗策略而非近似的公式。
       大量的工作都聚焦于使得近似推断模型类更具有表现力，如标准化流(Rezende & Mohamed, 2015; Kingma et al., 2016)通过结合一个简单的高斯后验和一个雅可比矩阵行列式易于处理的可逆的平滑映射，使得后验分布更加复杂；辅助变量VAEs (Maaløe et al., 2016)给后验分布添加了辅助的变量使它变得更灵活。然而，我们所知道的没有任何其他方法允许使用黑箱推断模型优化ELBO。

6.2、AVB与AAE的关系

       Makhzani et al. (Makhzani et al., 2015)提出了对抗自编码器的概念，这个想法就是将（2.4）中的项
$$\mathrm{K}\mathrm{L}(q_{\varphi }(z|x),p(z))(6.1)$$
替换成一个在式（6.2）收敛时强制执行的对抗损失。
$$\int q_{\varphi }(z|x)p_D(x)\mathrm{d}x\approx p(z)(6.2)$$
Makhzani et al. 的方法修改了变分目标函数，而我们的方法保留了这个目标函数。
       Makhzani et al. 的方法可以看做是我们的方法的一种近似，其中$T(x,z)$被限制为不依赖于$x$的一类函数。事实上，一个只依赖于$z$的理想的判别器最大化下式：
$$\int \int p_D(x)q(z|x)\log \sigma (T(z))\mathrm{d}x\mathrm{d}z+\int \int p_D(x)p(z)\log (1-\sigma (T(z)))\mathrm{d}x\mathrm{d}z,(6.3)$$
当且仅当下列情况成立：
$$T(z)=\log \int q(z|x)p_D(x)\mathrm{d}x-\log p(z).(6.4)$$
       显而易见，这个近似是第3节我们公式的一种粗暴的近似，但是Makhzani et al. 展示了这个方法仍然可以产生很好的采样结果。理论上，用这种方式限制$T(x,z)$确保了收敛时我们近似地可以得到：
$$\int q_{\varphi }(z|x)p_D(x)\mathrm{d}x=p(z),(6.5)$$
但是$q_{\varphi }(z|x)$需要接近于真实的后验$p_{\theta }(z|x)$。直觉上，通过$q_{\varphi }(z|x)$映射$p_D(x)$可以得到正确的边缘分布，分布中每个$x$的贡献可能非常不准确。
       与AAE相反，我们的目标是通过采用更好的概率推断提升ELBO，这允许我们的方法可以应用在更广泛的数据集上，因为我们只需要关注推断网络本身（参考第5节），并且这进一步提升了例如第4节中的自适应对比度（AC）这些在AAE中不可能提升的性能。

6.3、AVB与f-GANs的关系

       Nowozin et al. (Nowozin et al., 2016)提出将GANs推广到f散度。在这一小段中，我们将展示f散度允许将AVB表示成一个零和二人博弈游戏。
       f散度族由下式给出：
$$D_f(p||q)={\mathrm{E}}_{p}f(\frac{q(x)}{p(x)}),(6.6)$$
其中$f:R\to R_{\infty }$，并且$f(1)=0$。
       Nguyen et al. (2010)展示了通过采用$f$的凸共轭$f^{\ast }$，我们可以得到：
$$D_f(p||q)=\underset{T}{\sup }{\mathrm{E}}_{q(x)}[T(x)]-{\mathrm{E}}_{p(x)}[f^{\ast }(T(x))],(6.7)$$
其中，$T$是一个实值函数。特别地，当$f(t)=t\log t$时，这是一个反KL散度。因此我们可以得到：
$$\mathrm{K}\mathrm{L}(q(z|x),p(z))=D_f(p(z),q(z|x))=\underset{T}{\sup }{\mathrm{E}}_{q(z|x)}T(x,z)-{\mathrm{E}}_{p(z)}{f}^{\ast }(T(x,z)),(6.8)$$
其中$f^{\ast }(\xi )=\exp (\xi -1)$是$f(t)=t\log t$的凸共轭。
       总而言之，这可以产生下式：
$$\underset{\theta }{\max }{\mathrm{E}}_{p_D(x)}\log p_{\theta }(x)=\underset{\theta ,q}{\max }\underset{T}{\min }{\mathrm{E}}_{p_D(x)}{\mathrm{E}}_{p(z)}{f}^{\ast }(T(x,z))+{\mathrm{E}}_{p_D(x)}{\mathrm{E}}_{q(z|x)}(\log p_{\theta }(x|z)-T(x,z)).(6.9)$$
通过将（3.3）中判别器的目标函数替换成下式：
$$\underset{T}{\min }{\mathrm{E}}_{p_D(x)}[{\mathrm{E}}_{p(z)}{\mathrm{e}}^{T(x,z)-1}-{\mathrm{E}}_{q(z|x)}T(x,z)],(6.10)$$
我们可以将最大似然问题重新描述为一个最小最大零和博弈游戏。事实上，第3节的推导对于我们用来训练判别器的任意的f散度仍然有效，这与Poole et al. (Poole et al., 2016)的方法中提升GAN目标函数相似。实际上，可以观察到（6.10）目标函数导致了训练不稳定。因此我们采用了涉及到JS散度的标准GAN目标函数(3.3)。

6.4、AVB与BiGANs的关系

       BiGANs(Donahue et al., 2016; Dumoulin et al., 2016)是对GANs最近的一种扩展，目标是给生成模型添加了一个推断网络。与我们的方法类似，作者引入了作用于$(x,z)$数据点对和隐编码的对抗器。然而，尽管在BiGANs中对抗器用来分别优化生成网络和推断网络，我们的方法是共同优化生成网络和推断网络。结果我们的方法得到了对输入很好的重构，而在BiGANs中我们仅仅是间接得到这些重构的。

7、结论

       我们提出了一种基于对抗训练VAE的新方法，它使得推断模型更加灵活，并能有效地表示隐变量的几乎任何一种条件概率分布族。
       我们相信接下来可以更进一步地研究应用于对抗器、编码器网络和解码器网络的不同类别的神经网络结构，以及寻找更好的对比度分布。