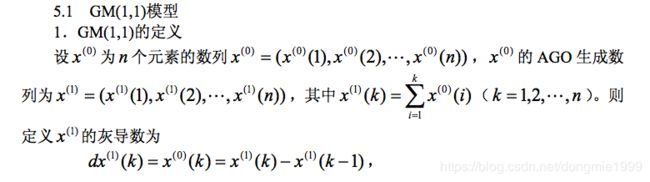数学建模各类算法学习笔记(附matlab代码)
目录
插值和拟合
线性规划
综合评价1:层次分析法(Analytic Hierarchy Process)AHP
综合评价2:Topsis(优劣解距离法)
最优解问题1:遗传算法Genitic algorithm ( GA )
最优解问题2:模拟退火算法Simulated annealing algorithm ( SA )
利用SPSS进行相关分析
MATLAB中的相关分析
对横截面数据分析预测:多元线性回归
使用SPSS对时间序列分析预测:季节分解、指数平滑方法和ARIMA模型
预测模型:灰色模型GM(Grey Model)
降维算法:主成分分析 ( Principal component analysis ) PCA
对随机发生的需求服务的系统分析预测:排队模型
传染病模型
微分方程建模
偏微分方程建模
使用Mathematica求解微分方程/差分方程
matlab求解偏微分方程
matlab快捷键
对于建模和编程的同学
1、假设很重要(题目中往往不提供数据或者提供很多数据,要恰当假设(即处理数据))
2、标准:假设合理、模型创造性、结果正确、表述清晰
3、十个较常用的(经典)算法:
3.1、蒙特卡洛(计算机仿真)
3.2、数据拟合、参数估计(最大似然、最大后验、最小二乘etc.)、插值等
3.3、线性规划、整数规划、二乘规划等(最优化问题,即最值求解问题,通常用Lingo软件实现)
3.4、图论算法(网络。选址等问题)
3.5、动态规划、回溯搜索、分支算法、分支界定etc.
3.6、对于很难写出目标函数的最优化问题(求最值问题):模拟退火法、神经网络、遗传算法
3.7、数值分析算法(方程组求解、矩阵运算、函数积分etc.)
3.8、网格算法和穷举法(搜索最优点、重点讨论模型本身而轻视算法时实用)
4、对于非线性规划问题(求解的目标函数是0/1或是分段函数etc.)
4.1、目标函数是分段函数的,要把分段函数写成一个函数才能求解. 如何把分段函数写成一个函数?
4.1.1、有几段就设置几个(组)自变量.(如有三段,则设置x1x2x3)
4.1.2、将各段的表达式用对应自变量写出并相加(如三段则为f(x) = f1(x1) + f2(x2) + f3(x3) )
4.1.3、对于2中的表达式设置约束(如0-5001x1为一段500-1000x2为一段,即 x2 > 500时 x1 为0一种写法是 (x1-500) x2 = 0 )
一些注意事项:
1、提交邮箱[email protected]
2、最终提交时间18号上午10点(最好提前一点交不然服务器可能卡,用注册的邮箱发比较好不然可能被退回)
3、邮件主题:Subject:2012xxx
4、论文命名:2012xxx.PDF
5、附件不应超过17M
6、正文中也要标注参考文献
7、比赛结束后24~48h登录官网查看提交的solution的状态
8、只能提交一次
9、论文最小号字体12pt
10、记得进入官网选题
11、简单、快、有效、令人容易读懂
12、摘要很重要
13、排版、画图也很重要
14、尽量以暖色为主
15、论文中不能出现关于身份的任何信息
16、有空可以自己查重(最好不超过20%)英文查重一般用turnitin(收费),也可翻译用中文查重
17、代码不推荐放在附录
选题具体操作步骤
一些算法的matlab源码参考
https://github.com/HuangCongQing/Algorithms_MathModels
https://github.com/liuzili97/MCM-ICM
往年论文
https://github.com/dick20/MCM-ICM
数据来源
https://max.book118.com/html/2019/0204/6232125043002005.shtm
https://blog.csdn.net/weixin_43102634/article/details/103696632
【简道云汇总】110+数据网站
虫部落数据搜索
【汇总】数据来源/大数据平台
大数据工具导航工具
数据平台
上面的数据多半都是宏观数据,微观数据市面上很少 大家可以在人大经济论坛搜索
另外也可以自己学习爬虫
MATLAB 绘制高精度海岸线地图教程
插值和拟合
插值是用现有数据来预测某个(些)指定点的数据(曲线要经过数据点)
拟合是用一个函数来描述所有现有的数据的规律(曲线不一定要经过数据点)
插值matlab实现
clear;
x = [0, 3, 5, 7, 9, 11, 12, 13, 14, 15];
y = [0, 1.2, 1.7, 2.0, 2.1, 2.0, 1.8, 1.2, 1.0, 1.6];
x1 = 0:0.1:15;
y1 = interp1(x, y, x1, 'spline');
% one dimension interpolation,
% x1 is the interpolated data,
% spline is the interpolate method, which includes linear,nearst,pchip,spline.
%'linear''nearest''next''previous''pchip''cubic''v5cubic''makima''spline' 默认为 'linear'
plot(x1, y1)spline为样条差值;linear:线性插值;nearest:最邻近插值;pchic:分段三次艾尔米特插值
interp1表一维线性插值
多项式拟合matlab实现
x = 1790:10:2010;
y = [3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6, 50.2,63.0,76.0,92.0,105.7,122.8,131.7,150.7,179.3,203.2,226.5,248.7,281.4,308.7];
plot(x,y,'*');
p = polyfit(x,y,3); % 3 means the number of fitting items,多项式的最高次项
polyval(p, 2020) % forecast 2010
plot(x, y, '*', x, polyval(p, x));
polyval(p, 2016)
线性规划
matlab中可用linprog求解. 以下为官方文档内容
x = linprog(f,A,b)f'*x such that A*x ≤ b.
x = linprog(f,A,b,Aeq,beq)Aeq*x = beq. Set A = [] and b = [] if no inequalities exist.
综合评价1:层次分析法(Analytic Hierarchy Process)AHP
用于评价模型,但是不建议在整个大的模型上使用(整道题目的模型),因为判断矩阵的主观性比较强
适用于指标较少的时候(n < 15, 因为一致性指标查表就到那里)
步骤如下:
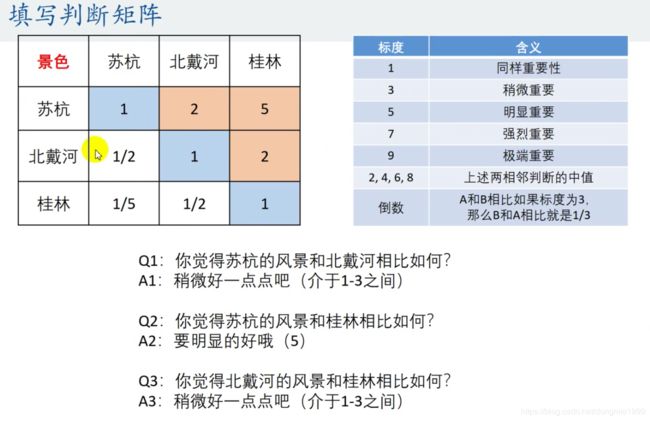
1、填写判断矩阵
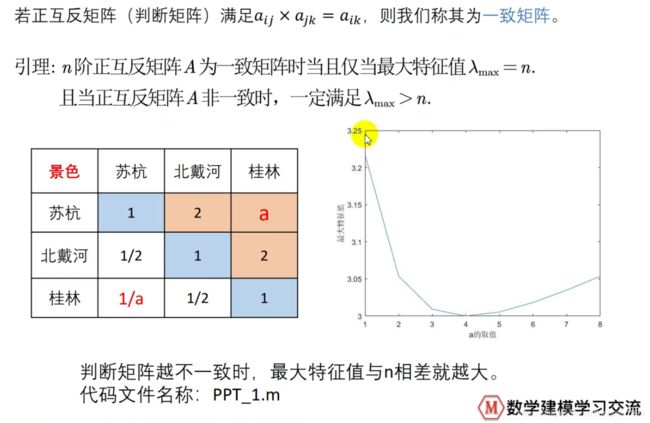
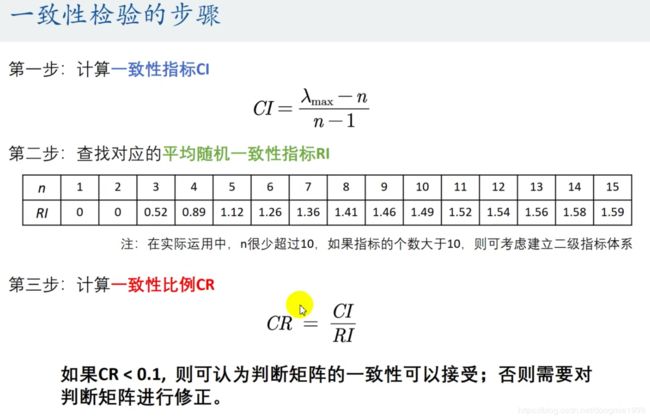
2、注意1中判断矩阵的一致性(希望对角线对称的互为倒数,主对角线上权全为1),可以不一致,但不能不一致太多。检验步骤如下
3、由判断矩阵得到权重(可根据算术平均、几何平均和特征值平均,特征值平均最为常用)
matlab代码如下 其中A为通过一致性检验的判断矩阵
%% 方法1:算术平均法求权重
% 第一步:将判断矩阵按照列归一化(每一个元素除以其所在列的和)
Sum_A = sum(A)
[n,n] = size(A) % 也可以写成n = size(A,1)
% 因为我们的判断矩阵A是一个方阵,所以这里的r和c相同,我们可以就用同一个字母n表示
SUM_A = repmat(Sum_A,n,1) %repeat matrix的缩写
clc;A
SUM_A
Stand_A = A ./ SUM_A
% 这里我们直接将两个矩阵对应的元素相除即可
% 第二步:将归一化的各列相加(按行求和)
sum(Stand_A,2)
% 第三步:将相加后得到的向量中每个元素除以n即可得到权重向量
disp('算术平均法求权重的结果为:');
disp(sum(Stand_A,2) / n)
% 首先对标准化后的矩阵按照行求和,得到一个列向量
% 然后再将这个列向量的每个元素同时除以n即可(注意这里也可以用./哦)
%% 方法2:几何平均法求权重
% 第一步:将A的元素按照行相乘得到一个新的列向量
clc;A
Prduct_A = prod(A,2)
% prod函数和sum函数类似,一个用于乘,一个用于加 dim = 2 维度是行
% 第二步:将新的向量的每个分量开n次方
Prduct_n_A = Prduct_A .^ (1/n)
% 这里对每个元素进行乘方操作,因此要加.号哦。 ^符号表示乘方哦 这里是开n次方,所以我们等价求1/n次方
% 第三步:对该列向量进行归一化即可得到权重向量
% 将这个列向量中的每一个元素除以这一个向量的和即可
disp('几何平均法求权重的结果为:');
disp(Prduct_n_A ./ sum(Prduct_n_A))
%% 方法3:特征值法求权重
% 第一步:求出矩阵A的最大特征值以及其对应的特征向量
clc
[V,D] = eig(A) %V是特征向量, D是由特征值构成的对角矩阵(除了对角线元素外,其余位置元素全为0)
Max_eig = max(max(D)) %也可以写成max(D(:))哦~
% 那么怎么找到最大特征值所在的位置了? 需要用到find函数,它可以用来返回向量或者矩阵中不为0的元素的位置索引。
% 那么问题来了,我们要得到最大特征值的位置,就需要将包含所有特征值的这个对角矩阵D中,不等于最大特征值的位置全变为0
% 这时候可以用到矩阵与常数的大小判断运算
D == Max_eig
[r,c] = find(D == Max_eig , 1)
% 找到D中第一个与最大特征值相等的元素的位置,记录它的行和列。
% 第二步:对求出的特征向量进行归一化即可得到我们的权重
V(:,c)
disp('特征值法求权重的结果为:');
disp( V(:,c) ./ sum(V(:,c)) )
% 我们先根据上面找到的最大特征值的列数c找到对应的特征向量,然后再进行标准化。4、根据权重算出每个备选的得分(excel中按F4即可锁定单元格),得分最高者是好的
综合评价2:Topsis(优劣解距离法)
适用于指标较多 / 指标之间的排序已知的时候(可以做更客观更精确的评价)
中心思想↓
matlab实现如下
[n,m] = size(X);
disp(['共有' num2str(n) '个评价对象, ' num2str(m) '个评价指标'])
Judge = input(['这' num2str(m) '个指标是否需要经过正向化处理,需要请输入1 ,不需要输入0: ']);
if Judge == 1
Position = input('请输入需要正向化处理的指标所在的列,例如第2、3、6三列需要处理,那么你需要输入[2,3,6]: '); %[2,3,4]
disp('请输入需要处理的这些列的指标类型(1:极小型, 2:中间型, 3:区间型) ')
Type = input('例如:第2列是极小型,第3列是区间型,第6列是中间型,就输入[1,3,2]: '); %[2,1,3]
% 注意,Position和Type是两个同维度的行向量
for i = 1 : size(Position,2) %这里需要对这些列分别处理,因此我们需要知道一共要处理的次数,即循环的次数
X(:,Position(i)) = Positivization(X(:,Position(i)),Type(i),Position(i));
% Positivization是我们自己定义的函数,其作用是进行正向化,其一共接收三个参数
% 第一个参数是要正向化处理的那一列向量 X(:,Position(i)) 回顾上一讲的知识,X(:,n)表示取第n列的全部元素
% 第二个参数是对应的这一列的指标类型(1:极小型, 2:中间型, 3:区间型)
% 第三个参数是告诉函数我们正在处理的是原始矩阵中的哪一列
% 该函数有一个返回值,它返回正向化之后的指标,我们可以将其直接赋值给我们原始要处理的那一列向量
end
disp('正向化后的矩阵 X = ')
disp(X)
end
%% 第三步:对正向化后的矩阵进行标准化
Z = X ./ repmat(sum(X.*X) .^ 0.5, n, 1);
disp('标准化矩阵 Z = ')
disp(Z)
%% 第四步:计算与最大值的距离和最小值的距离,并算出得分
D_P = sum([(Z - repmat(max(Z),n,1)) .^ 2 ],2) .^ 0.5; % D+ 与最大值的距离向量
D_N = sum([(Z - repmat(min(Z),n,1)) .^ 2 ],2) .^ 0.5; % D- 与最小值的距离向量
S = D_N ./ (D_P+D_N); % 未归一化的得分
disp('最后的得分为:')
stand_S = S / sum(S)
[sorted_S,index] = sort(stand_S ,'descend')
最优解问题1:遗传算法Genitic algorithm ( GA )
初始化一个种群,由父辈产生子辈不断迭代
需指定的变量:迭代倍数,变异几率,基因的长度etc.
- 函数crossover:由父本和母本产生孩子
- 函数mutation:以一定的几率变异(二进制中为简单的0与1对调,实数范围内以原本的基因为均值,变异强度为方差产生一个随机数)
- 函数translate:把基因翻译为性状,即如何从基因中挑选好的个体
- 函数ranking:挑选出每一代中性状最好的
注:进化算法为改进过的遗传算法,保留了性状优良的父辈(父辈与子辈进行竞争,赢的一方原封不动保留,输的一方的基因朝着赢的一方的基因改变一点再放回去迭代)
最优解问题2:模拟退火算法Simulated annealing algorithm ( SA )
不需要初始化种群(可以随机生成一个解)
每次对当前解产生一个扰动(这个扰动就是温度,温度越高扰动越大)得到新解,接受更好的新解,或根据一定概率接受性状不如当前解的新解
SA参考教程
利用SPSS进行相关分析
使用对象:几个变量,且每个变量只有一列的数据(如果不是则使用求平均的方法来降维成只有一列)
- 打开.sav文件(SPSS也可直接打开excel文件,保存成spss文件就是.sav了)
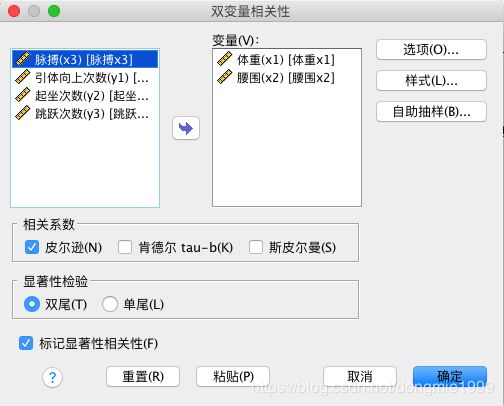
- 菜单栏 -> 分析 -> 双变量 添加想要分析相关性的变量,默认选择皮尔逊和显示显著相关性
- 某两个数据相关分析如下,Sig. 大于 0.05 说明显著相关,皮尔逊相关性大于零说明成正相关
中介效应:X ---M--->Y X通过M影响Y
在SPSS中利用process插件进行中介效应分析参考此教程
MATLAB中的相关分析
matlab描述基本统计量的函数
使用corrcoef(Test)来获得一个相关系数矩阵
其中Test是一个矩阵,矩阵的每一列是一个变量
相关分析通常与假设检验连在一起
如何用最通俗易懂的方式理解假设检验
对横截面数据分析预测:多元线性回归
横截面数据:同一时间收集到的不同数据
探究一个或多个自变量X1, X2 ,X3 ...对因变量Y的影响,达到通过 X 预测 Y 的目的。
注意:可以说是X与Y相关,但不能轻易说因为X所以Y,相关性不是因果性( e.g. 冰淇淋的销量与游泳死亡人数呈正相关)
要注意蒙特卡洛仿真的内生性(扰动项 μ 与变量 x1, x2, x3 ...无关,即 y = f(x1, x2, x3 ...) 函数应包括所有自变量,或者至少包括我们感兴趣的变量,即将变量分为核心解释变量和控制变量两类)
何时取对数:
伍德里奇的《计量经济学导论,现代观点》里,第六章176-177页有详细的论述; 取对数意味着原被解释变量对解释变量的弹性,即百分比的变化而不是数值的变化;目前,对于什么时候取对数还没有固定的规则,但是有一些经验法则:
(1)与市场价值相关的,例如,价格、销售额、工资等都可以取对数; (2)以年度量的变量,如受教育年限、工作经历等通常不取对数; (3)比例变量,如失业率、参与率等,两者均可; (4)变量取值必须是非负数,如果包含0,则可以对y取对数ln(1+y);
取对数的好处:(1)减弱数据的异方差性(2)如果变量本身不符合正态分布,取 了对数后可能渐近服从正态分布(3)模型形式的需要,让模型具有经济学意义。
为了更为精准的研究影响评价量的重要因素(去除量纲的影响), 我们可考虑使用标准化回归系数。
对数据进行标准化,就是将原始数据减去它的均数后,再除以该变量的标准差,计算得到新的变量值,新变量构成的回归方程称为标准化
回归方程,回归后相应可得到标准化回归系数。
标准化系数的绝对值越大,说明对因变量的影响就越大(只关注显著的回归系数哦)。
使用SPSS对时间序列分析预测:季节分解、指数平滑方法和ARIMA模型
时间序列:不同时间收集到的同一序列
时间序列通常有这个四种规律:
- 长期变动趋势T :持续上升/持续下降
- 季节变动规律S :随着季节(月、季或周,不能以年为单位)变动
- 周期变动规律C :遵循某一周期变化
- 不规则变动(随即扰动项)I :无规则
一般的时间序列可以用上述四种规律描述
SPSS对时间序列建模的思路
(1)处理数据的缺失值问题、生成时间变量并画出时间序列图;
(2)数据是否为季度数据或者月份数据(至少有两个完整的周期,即两年),如果是的话则要观察图形中是否存在季节性波动。
(3)根据时间序列图大致判断数据是否为平稳序列(数据围绕着均值上下波动, 无趋势和季节性)
(4)打开Spss,分析‐‐时间序列预测—创建传统模型(高版本的Spss可能才有这个功能哦,我用的是24版本),看看Spss专家建模器得出的最优的模型类型。
(5)如果最后的结果是ARIMA(p,0,q)模型,那么我们就可以画出时间序列的样本ACF和PACF图形进行分析;如果得到的是ARIMA(p,1,q)模型,我们可以先对数据进行1阶差分后再用ACF和PACF图形分析;如果得到的结果与季节性相关,那么我们可以考虑使用时间序列分解。
tips :
SPSS中在输出的图片右键->export->在document框里,type选none->在graphics框里选择保存路径,就可以保存为JPGF等图片格式了
预测两要:
一要结合背景;
二要合理假设。
预测两不要:
不要硬套模型;
不要不做解释。
预测模型:灰色模型GM(Grey Model)
已知信息较少但要做判断,就是灰色预测
一般使用累加生成(AGO)数据,用累减生成(IAGO)还原数据,常用的数据生成方法还有均值生成 z(k) = αx(k) + (1-α)x(k-1)
检验:①级比(应在可容覆盖范围内)②残差和级比偏差值(小于0.2)
可参考这篇文章
降维算法:主成分分析 ( Principal component analysis ) PCA
核心思想:用较少的新变量代替原来较多的旧变量,而且使这些较少的新变量尽可能多地保留原来变量所反映的信息
PCA的一般步骤如下
注:相关系数与协方差的关系如下,数值上差了一个方差
主成分分析最重要是解释降维后变量的意义 / 这个降维结果说明了什么
对随机发生的需求服务的系统分析预测:排队模型
四个常用模型:
(1) M/M/S/∞表示输入过程是 Poisson 流,服务时间服从负指数分布,系统有 S 个服务台平行服务,系统为容量无穷大的等待制排队系统。
(2) M/G/S/∞表示输入过程是 Poisson 流,服务时间服从一般概率分布,系统有 S 个服务台平行服务,系统容量无穷大的等待制排队系统。
(3)D/M/S/K 表示顾客相继到达时间间隔独立、服从定长分布,服务时间服从负指数分布,系统有 S 个服务台平行服务,系统容量为 K 个的混合制系统。
(4) M/M/S/S 表示输入过程是 Poisson 流,服务时间服从负指数分布,系统有 S 个服务台平行服务,顾客到达后不等待的损失制系统。
(5)M/M/S/K/K 表示输入过程是 Poisson 流,服务时间服从负指数分布,系统有 S 个服务台平行服务,系统容量和顾客容量都为 K 个的闭合制系统。
注:泊松分布和指数分布的区别与联系
一些常用指标:
2、排队系统的数量指标
(1)队长与等待队长
队长(通常记为 Ls )是指系统中的平均顾客数(包括正在接受服务的顾客)。等待队长(通常记为 Lq )指系统中处于等待的顾客的数量。显然,队长等于等待队长加上正在服务的顾客数。
(2)等待时间
等待时间包括顾客的平均逗留时间(通常记为Ws )和平均等待时间(通常记为Wq )。 顾客的平均逗留时间是指顾客进入系统到离开系统这段时间,包括等待时间和接受服务的时间。顾客的平均等待时间是指顾客进入系统到接受服务这段时间。
(3)忙期
从顾客到达空闲的系统,服务立即开始,直到再次变为空闲,这段时间是系统连续繁忙 的时期,称之为系统的忙期。它反映了系统中服务机构工作强度,是衡量服务系统利用效率 的指标,即服务强度=忙期/服务总时间=1─闲期/服务总时间 闲期与忙期对应的系统的空闲时间,也就是系统连续保持空闲的时间长度。 计算这些指标的基础是表达系统状态的概率。所谓系统的状态是指系统中的顾客数,如果系统中有 n 个顾客就说系统的状态是 n,它可能的数值是:
1队长没有限制时,n=0,1,2,...,
2队长有限制,最大数为 N,则 n=0,1,2,...,N
3即时制,服务台个数为 c 时,n=0,1,2,...,c。该状态又表示正在工作的服务台数。
传染病模型
四种人,都是时间的函数
S (susceptible) --> E (exposed) --> I (infectious) --> R (recovered)
本质上是一种微分方程建模求解,常用到的模型如logistic函数
微分方程建模
微分方程对应连续量,差分方程对应离散量
- 当成物理题来做,为简化问题套用易求解的理想模型时,需要做的假设(质量均分分布、阻力其他星球引力等可忽略、直线运动等)可认为是基本假设
- 通常会用到的:质量守恒、能量守恒、简单的动力学公式etc.
- 建好模型之后,如有数据应使用数据对模型进行测试检验(建出的模是否符合实际),如不符合思考应修改模型中的那些部分使符合
偏微分方程建模
- 第一类边界条件:
给出未知函数在边界上的数值;
- 第二类边界条件:
给出未知函数在边界外法线的方向导数;
- 第三类边界条件:
给出未知函数在边界上的函数值和外法线的方向导数的线性组合。
使用Mathematica求解微分方程/差分方程
matlab求解偏微分方程
参考教程
此教程中标准化过程如下
注:最终的求出来的u1和u2是一些数值(而不是具体的函数),可以plot出来观察
matlab的APP中海油一个叫PDE的工具箱可以查看使用教程
matlab快捷键
撤销 Ctrl + Z
重做 Shift + Ctrl + Z
多段注释 Ctrl + /
取消多段注释 Ctrl + T
智能缩进 Ctrl + I
补全命令 Tab
附:赛美官网rules的一段
a. Summary Sheet: The summary is an essential part of your MCM/ICM paper and should appear as the first page of your solution report. The judges place considerable weight on the summary, and winning papers are often distinguished from other papers based on the quality of the summary. Click here to download the Microsoft Word Summary Sheet.
• To write a good summary, imagine that a reader will choose whether to read the body of the paper based on your summary: Your concise presentation in the summary should inspire a reader to learn about the details of your work.
• You should write the summary last, as it should clearly describe your approach to the problem and, most prominently, your most important conclusions. Ensure you plan time after solving your problem to write a comprehensive and articulate summary.
• Summaries that are mere restatements of the contest problem, or are a cut-and-paste boilerplate from the Introduction are generally considered to be weak.
b. Overall: The team’s solution should be articulate, concise, and organized in order to allow the reader to easily follow the solution process and conclusions. Key statements should present major ideas and results.
• A Table of Contents assists the reader in previewing the organization of your report.
• Present a clarification or restatement of the problem as appropriate.
• Present a clear exposition of all variables and hypotheses.
• State and justify reasonable assumptions that bear on the problem.
• Present an analysis of the problem, motivating or justifying the model being used.
• Summarize derivations, computations, or illustrative examples in the main body of the solution, and leave lengthy derivations and/or calculations and data in appropriate appendices.
• Include a design of the model. Discuss how the model could be tested, to include error analysis, sensitivity, and/or stability.
• Discuss any apparent strengths or weaknesses to your model or approach.
• Provide a conclusion and report results explicitly.
• Document resources and references.