[转]机器学习算法库：liblinear/LibShortText

SVM原理简介：最大间隔分类器

SVM是一种二类分类模型，其求解目标在于确定一个分类的超平面，以最大化特征空间上的间隔。分类超平面的确定只取决于少数的样本信息，这些关键的样本被称之为支持向量Support Vector，这也是SVM—支持向量机名称的由来。

首先我们举一个二维空间的小例子，并假设样本是线性可分的，这样我们就可以在二维空间里划一条直线（高维空间的超平面在二维空间表现为直线），完全分开所有的正负样本。那么引出一个问题，显然存在多条区分正负样本的直线（例如下图的实线和虚线），哪条是更好的选择？

线性分类超平面

从直观上我们希望正负样本分得越开越好，也就是正负样本之间的几何间隔越大越好。这是因为距离分类超平面越近的样本，分类的置信度越低（实际上几何间隔代表了分类器的误差上界）。SVM的优化目标，正是最大化最接近分类超平面的点到分类超平面的距离。
我们把这个二维的分类超平面设为 f(x)=wTx+b=0 。把样本 x 代入 f(x) 中，如果得到的结果小于0，我们对该样本标一个-1的类别标签 yi ，大于0则标一个+1的 yi 。（约定为+1或-1只是为了下面的推导便利而已）。
首先定义函数间隔（function margin）：

γˆ=|wTx+b|=yi(wTx+b)

注意前面乘上 yi 可以保证这个margin的非负性（因为 f(x)<0 对应 yi=−1 的那些样本）。
如下图所示，对任意不在分类超平面上的点 xi ，我们可以依赖它到分类超平面的垂直投影 x0 ，计算出它到分类超平面上的几何间隔（geometrical margin）：

γ˜=|wTxi+b|||w||=yi(wTx+b)||w||=γˆ||w||

（ ||w|| 是向量 w 的范数，是对 w 长度的一种度量）。于是我们得到了函数间隔和几何间隔的数值关系。

几何间隔

假定所有样本到分类超平面的函数间隔最小值表示为 γˆ ，我们可以把SVM的优化问题描述成以下表达式：
maxγ˜=γˆ/||w||,s.t.yi(wTx+b)>=γˆ,i=1,…,n
由于 γˆ 和 ||w|| 是线性关联的，而即便在超平面固定的情况下， ||w|| 仍是可变化的（只要 b 随着 ||w|| 等比缩放，比如 x1+x2+1=0 和 2x1+2x2+2=0 其实是一个平面），那么 γˆ 实际上不影响SVM优化问题的求解，为了简化问题，我们设 γˆ=1 ，从而把优化问题转化为：

maxγ˜=1/||w||,s.t.yi(wTx+b)>=1,i=1,…,n

这个问题可以转化为一个等价的二次规划问题，也就是说它必然能得到一个全局的最优解。
通过求解这个问题，我们可以得到了一个最大化几何间隔的分类超平面（如下图红线所示），另外两条线到红线的距离都等于 1/||w|| ，而橘黄色的样本就是支持向量Support Vector。

最优超平面和支持向量

到此为止，通过最大化几何间隔，使得该分类器对样本分类时有了最大的置信度，准确的说，是对置信度最小的样本有了最大的置信度，这正是SVM的核心思想。

文章来源：http://guoze.me/2014/07/14/svm-introduction/

分类算法之朴素贝叶斯分类 (Naive Bayesian classification)

0、写在前面的话

      我个人一直很喜欢算法一类的东西，在我看来算法是人类智慧的精华，其中蕴含着无与伦比的美感。而每次将学过的算法应用到实际中，并解决了实际问题后，那种快感更是我在其它地方体会不到的。

      一直想写关于算法的博文，也曾写过零散的两篇，但也许是相比于工程性文章来说太小众，并没有引起大家的兴趣。最近面临毕业找工作，为了能给自己增加筹码，决定再次复习算法方面的知识，我决定趁这个机会，写一系列关于算法的文章。这样做，主要是为了加强自己复习的效果，我想，如果能将复习的东西用自己的理解写成文章，势必比单纯的读书做题掌握的更牢固，也更能触发自己的思考。如果能有感兴趣的朋友从中有所收获，那自然更好。

      这个系列我将其命名为“算法杂货铺”，其原因就是这些文章一大特征就是“杂”，我不会专门讨论堆栈、链表、二叉树、查找、排序等任何一本数据结构教科书都会讲的基础内容，我会从一个“专题”出发，如概率算法、分类算法、NP问题、遗传算法等，然后做一个引申，可能会涉及到算法与数据结构、离散数学、概率论、统计学、运筹学、数据挖掘、形式语言与自动机等诸多方面，因此其内容结构就像一个杂货铺。当然，我会竭尽所能，尽量使内容“杂而不乱”。

1.1、摘要

      贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。本文作为分类算法的第一篇，将首先介绍分类问题，对分类问题进行一个正式的定义。然后，介绍贝叶斯分类算法的基础——贝叶斯定理。最后，通过实例讨论贝叶斯分类中最简单的一种：朴素贝叶斯分类。

1.2、分类问题综述

      对于分类问题，其实谁都不会陌生，说我们每个人每天都在执行分类操作一点都不夸张，只是我们没有意识到罢了。例如，当你看到一个陌生人，你的脑子下意识判断TA是男是女；你可能经常会走在路上对身旁的朋友说“这个人一看就很有钱、那边有个非主流”之类的话，其实这就是一种分类操作。

      从数学角度来说，分类问题可做如下定义：

      已知集合：和，确定映射规则，使得任意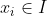有且仅有一个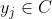使得成立。（不考虑模糊数学里的模糊集情况）

      其中C叫做类别集合，其中每一个元素是一个类别，而I叫做项集合，其中每一个元素是一个待分类项，f叫做分类器。分类算法的任务就是构造分类器f。

      这里要着重强调，分类问题往往采用经验性方法构造映射规则，即一般情况下的分类问题缺少足够的信息来构造100%正确的映射规则，而是通过对经验数据的学习从而实现一定概率意义上正确的分类，因此所训练出的分类器并不是一定能将每个待分类项准确映射到其分类，分类器的质量与分类器构造方法、待分类数据的特性以及训练样本数量等诸多因素有关。

      例如，医生对病人进行诊断就是一个典型的分类过程，任何一个医生都无法直接看到病人的病情，只能观察病人表现出的症状和各种化验检测数据来推断病情，这时医生就好比一个分类器，而这个医生诊断的准确率，与他当初受到的教育方式（构造方法）、病人的症状是否突出（待分类数据的特性）以及医生的经验多少（训练样本数量）都有密切关系。

1.3、贝叶斯分类的基础——贝叶斯定理

      每次提到贝叶斯定理，我心中的崇敬之情都油然而生，倒不是因为这个定理多高深，而是因为它特别有用。这个定理解决了现实生活里经常遇到的问题：已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率：

      表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。其基本求解公式为：。

      贝叶斯定理之所以有用，是因为我们在生活中经常遇到这种情况：我们可以很容易直接得出P(A|B)，P(B|A)则很难直接得出，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。

      下面不加证明地直接给出贝叶斯定理：

      

1.4、朴素贝叶斯分类

1.4.1、朴素贝叶斯分类的原理与流程

      朴素贝叶斯分类是一种十分简单的分类算法，叫它朴素贝叶斯分类是因为这种方法的思想真的很朴素，朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。通俗来说，就好比这么个道理，你在街上看到一个黑人，我问你你猜这哥们哪里来的，你十有八九猜非洲。为什么呢？因为黑人中非洲人的比率最高，当然人家也可能是美洲人或亚洲人，但在没有其它可用信息下，我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础。

      朴素贝叶斯分类的正式定义如下：

      1、设为一个待分类项，而每个a为x的一个特征属性。

      2、有类别集合。

      3、计算。

      4、如果，则。

      那么现在的关键就是如何计算第3步中的各个条件概率。我们可以这么做：

      1、找到一个已知分类的待分类项集合，这个集合叫做训练样本集。

      2、统计得到在各类别下各个特征属性的条件概率估计。即。

      3、如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：

      

      因为分母对于所有类别为常数，因为我们只要将分子最大化皆可。又因为各特征属性是条件独立的，所以有：

      

      根据上述分析，朴素贝叶斯分类的流程可以由下图表示（暂时不考虑验证）：

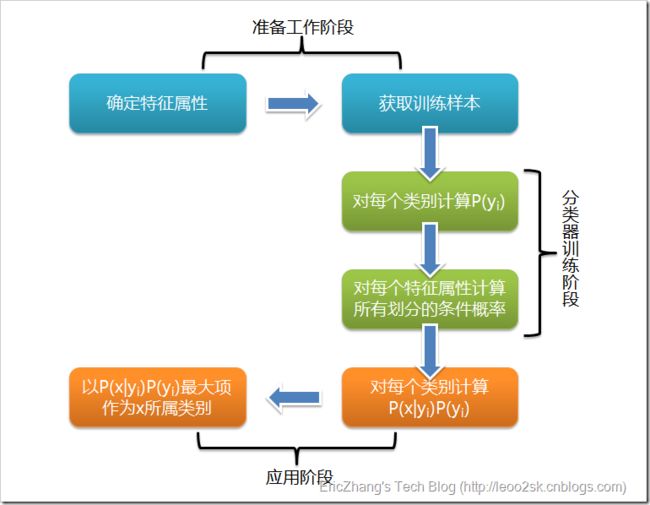
      可以看到，整个朴素贝叶斯分类分为三个阶段：

      第一阶段——准备工作阶段，这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

      第二阶段——分类器训练阶段，这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。

      第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

1.4.2、估计类别下特征属性划分的条件概率及Laplace校准

      这一节讨论P(a|y)的估计。

      由上文看出，计算各个划分的条件概率P(a|y)是朴素贝叶斯分类的关键性步骤，当特征属性为离散值时，只要很方便的统计训练样本中各个划分在每个类别中出现的频率即可用来估计P(a|y)，下面重点讨论特征属性是连续值的情况。

      当特征属性为连续值时，通常假定其值服从高斯分布（也称正态分布）。即：

      

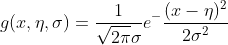
      而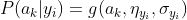

      因此只要计算出训练样本中各个类别中此特征项划分的各均值和标准差，代入上述公式即可得到需要的估计值。均值与标准差的计算在此不再赘述。

      另一个需要讨论的问题就是当P(a|y)=0怎么办，当某个类别下某个特征项划分没有出现时，就是产生这种现象，这会令分类器质量大大降低。为了解决这个问题，我们引入Laplace校准，它的思想非常简单，就是对没类别下所有划分的计数加1，这样如果训练样本集数量充分大时，并不会对结果产生影响，并且解决了上述频率为0的尴尬局面。

1.4.3、朴素贝叶斯分类实例：检测SNS社区中不真实账号

      下面讨论一个使用朴素贝叶斯分类解决实际问题的例子，为了简单起见，对例子中的数据做了适当的简化。

      这个问题是这样的，对于SNS社区来说，不真实账号（使用虚假身份或用户的小号）是一个普遍存在的问题，作为SNS社区的运营商，希望可以检测出这些不真实账号，从而在一些运营分析报告中避免这些账号的干扰，亦可以加强对SNS社区的了解与监管。

      如果通过纯人工检测，需要耗费大量的人力，效率也十分低下，如能引入自动检测机制，必将大大提升工作效率。这个问题说白了，就是要将社区中所有账号在真实账号和不真实账号两个类别上进行分类，下面我们一步一步实现这个过程。

      首先设C=0表示真实账号，C=1表示不真实账号。

      1、确定特征属性及划分

      这一步要找出可以帮助我们区分真实账号与不真实账号的特征属性，在实际应用中，特征属性的数量是很多的，划分也会比较细致，但这里为了简单起见，我们用少量的特征属性以及较粗的划分，并对数据做了修改。

      我们选择三个特征属性：a1：日志数量/注册天数，a2：好友数量/注册天数，a3：是否使用真实头像。在SNS社区中这三项都是可以直接从数据库里得到或计算出来的。

      下面给出划分：a1：{a<=0.05, 0.05=0.2}，a1：{a<=0.1, 0.1=0.8}，a3：{a=0（不是）,a=1（是）}。

      2、获取训练样本

      这里使用运维人员曾经人工检测过的1万个账号作为训练样本。

      3、计算训练样本中每个类别的频率

      用训练样本中真实账号和不真实账号数量分别除以一万，得到：

      

      

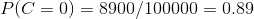
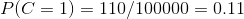
      4、计算每个类别条件下各个特征属性划分的频率

      

      

      

      

      

      

      

      

      

      

      

      

      

      

      

      

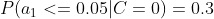
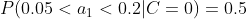
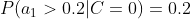
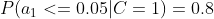
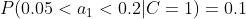
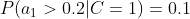
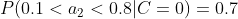
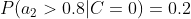
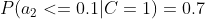
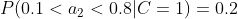
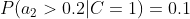
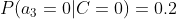
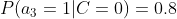
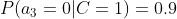
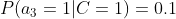
      5、使用分类器进行鉴别

      下面我们使用上面训练得到的分类器鉴别一个账号，这个账号使用非真实头像，日志数量与注册天数的比率为0.1，好友数与注册天数的比率为0.2。

      

      

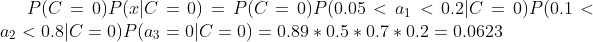
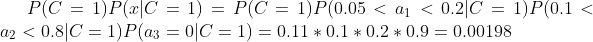
      可以看到，虽然这个用户没有使用真实头像，但是通过分类器的鉴别，更倾向于将此账号归入真实账号类别。这个例子也展示了当特征属性充分多时，朴素贝叶斯分类对个别属性的抗干扰性。

1.5、分类器的评价

      虽然后续还会提到其它分类算法，不过这里我想先提一下如何评价分类器的质量。

      首先要定义，分类器的正确率指分类器正确分类的项目占所有被分类项目的比率。

      通常使用回归测试来评估分类器的准确率，最简单的方法是用构造完成的分类器对训练数据进行分类，然后根据结果给出正确率评估。但这不是一个好方法，因为使用训练数据作为检测数据有可能因为过分拟合而导致结果过于乐观，所以一种更好的方法是在构造初期将训练数据一分为二，用一部分构造分类器，然后用另一部分检测分类器的准确率。

文章来源：http://www.cnblogs.com/leoo2sk/archive/2010/09/17/1829190.html

朴素贝叶斯分类器的应用

生活中很多场合需要用到分类，比如新闻分类、病人分类等等。

本文介绍朴素贝叶斯分类器（Naive Bayes classifier），它是一种简单有效的常用分类算法。

一、病人分类的例子

让我从一个例子开始讲起，你会看到贝叶斯分类器很好懂，一点都不难。

某个医院早上收了六个门诊病人，如下表。

　　症状　　职业　　　疾病

　　打喷嚏　护士　　　感冒 
　　打喷嚏　农夫　　　过敏 
　　头痛　　建筑工人　脑震荡 
　　头痛　　建筑工人　感冒 
　　打喷嚏　教师　　　感冒 
　　头痛　　教师　　　脑震荡

现在又来了第七个病人，是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大？

根据贝叶斯定理：

　P(A|B) = P(B|A) P(A) / P(B)

可得

　　　P(感冒|打喷嚏x建筑工人) 
　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
　　　　/ P(打喷嚏x建筑工人)

假定"打喷嚏"和"建筑工人"这两个特征是独立的，因此，上面的等式就变成了

　　　P(感冒|打喷嚏x建筑工人) 
　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒) 
　　　　/ P(打喷嚏) x P(建筑工人)

这是可以计算的。

　　P(感冒|打喷嚏x建筑工人) 
　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
　　　　= 0.66

因此，这个打喷嚏的建筑工人，有66%的概率是得了感冒。同理，可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率，就可以知道他最可能得什么病。

这就是贝叶斯分类器的基本方法：在统计资料的基础上，依据某些特征，计算各个类别的概率，从而实现分类。

二、朴素贝叶斯分类器的公式

假设某个体有n项特征（Feature），分别为F₁、F₂、...、F_n。现有m个类别（Category），分别为C₁、C₂、...、C_m。贝叶斯分类器就是计算出概率最大的那个分类，也就是求下面这个算式的最大值：

　P(C|F1F2...Fn) 
　　= P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

由于 P(F1F2...Fn) 对于所有的类别都是相同的，可以省略，问题就变成了求

　P(F1F2...Fn|C)P(C)

的最大值。

朴素贝叶斯分类器则是更进一步，假设所有特征都彼此独立，因此

　P(F1F2...Fn|C)P(C) 
　　= P(F1|C)P(F2|C) ... P(Fn|C)P(C)

上式等号右边的每一项，都可以从统计资料中得到，由此就可以计算出每个类别对应的概率，从而找出最大概率的那个类。

虽然"所有特征彼此独立"这个假设，在现实中不太可能成立，但是它可以大大简化计算，而且有研究表明对分类结果的准确性影响不大。

下面再通过两个例子，来看如何使用朴素贝叶斯分类器。

三、账号分类的例子

本例摘自张洋的《算法杂货铺----分类算法之朴素贝叶斯分类》。

根据某社区网站的抽样统计，该站10000个账号中有89%为真实账号（设为C₀），11%为虚假账号（设为C₁）。

　　C0 = 0.89

　　C1 = 0.11

接下来，就要用统计资料判断一个账号的真实性。假定某一个账号有以下三个特征：

　　　　F1: 日志数量/注册天数 
　　　　F2: 好友数量/注册天数 
　　　　F3: 是否使用真实头像（真实头像为1，非真实头像为0）

　　　　F1 = 0.1 
　　　　F2 = 0.2 
　　　　F3 = 0

请问该账号是真实账号还是虚假账号？

方法是使用朴素贝叶斯分类器，计算下面这个计算式的值。

　　　　P(F1|C)P(F2|C)P(F3|C)P(C)

虽然上面这些值可以从统计资料得到，但是这里有一个问题：F1和F2是连续变量，不适宜按照某个特定值计算概率。

一个技巧是将连续值变为离散值，计算区间的概率。比如将F1分解成[0, 0.05]、(0.05, 0.2)、[0.2, +∞]三个区间，然后计算每个区间的概率。在我们这个例子中，F1等于0.1，落在第二个区间，所以计算的时候，就使用第二个区间的发生概率。

根据统计资料，可得：

　　P(F1|C0) = 0.5, P(F1|C1) = 0.1 
　　P(F2|C0) = 0.7, P(F2|C1) = 0.2 
　　P(F3|C0) = 0.2, P(F3|C1) = 0.9

因此，

　　P(F1|C0) P(F2|C0) P(F3|C0) P(C0) 
　　　　= 0.5 x 0.7 x 0.2 x 0.89 
　　　　= 0.0623

　　P(F1|C1) P(F2|C1) P(F3|C1) P(C1) 
　　　　= 0.1 x 0.2 x 0.9 x 0.11 
　　　　= 0.00198

可以看到，虽然这个用户没有使用真实头像，但是他是真实账号的概率，比虚假账号高出30多倍，因此判断这个账号为真。

四、性别分类的例子

本例摘自维基百科，关于处理连续变量的另一种方法。

下面是一组人类身体特征的统计资料。

　　性别　　身高（英尺）　体重（磅）　　脚掌（英寸）

　　男 　　　6 　　　　　　180　　　　　12 
　　男 　　　5.92　　　　　190　　　　　11 
　　男 　　　5.58　　　　　170　　　　　12 
　　男 　　　5.92　　　　　165　　　　　10 
　　女 　　　5 　　　　　　100　　　　　6 
　　女 　　　5.5 　　　　　150　　　　　8 
　　女 　　　5.42　　　　　130　　　　　7 
　　女 　　　5.75　　　　　150　　　　　9

已知某人身高6英尺、体重130磅，脚掌8英寸，请问该人是男是女？

根据朴素贝叶斯分类器，计算下面这个式子的值。

P(身高|性别) x P(体重|性别) x P(脚掌|性别) x P(性别)

这里的困难在于，由于身高、体重、脚掌都是连续变量，不能采用离散变量的方法计算概率。而且由于样本太少，所以也无法分成区间计算。怎么办？

这时，可以假设男性和女性的身高、体重、脚掌都是正态分布，通过样本计算出均值和方差，也就是得到正态分布的密度函数。有了密度函数，就可以把值代入，算出某一点的密度函数的值。

比如，男性的身高是均值5.855、方差0.035的正态分布。所以，男性的身高为6英尺的概率的相对值等于1.5789（大于1并没有关系，因为这里是密度函数的值，只用来反映各个值的相对可能性）。

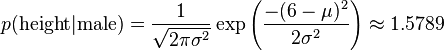
有了这些数据以后，就可以计算性别的分类了。

　　P(身高=6|男) x P(体重=130|男) x P(脚掌=8|男) x P(男) 
　　　　= 6.1984 x e^-9

　　P(身高=6|女) x P(体重=130|女) x P(脚掌=8|女) x P(女) 
　　　　= 5.3778 x e^-4

可以看到，女性的概率比男性要高出将近10000倍，所以判断该人为女性。

（完）

文章来源：http://www.ruanyifeng.com/blog/2013/12/naive_bayes_classifier.html

Libsvm和Liblinear的使用经验谈

 Libsvm和Liblinear都是国立台湾大学的Chih-Jen Lin博士开发的，Libsvm主要是用来进行非线性svm 分类器的生成，提出有一段时间了，而Liblinear则是去年才创建的，主要是应对large-scale的data classification，因为linear分类器的训练比非线性分类器的训练计算复杂度要低很多，时间也少很多，而且在large scale data上的性能和非线性的分类器性能相当，所以Liblinear是针对大数据而生的。

   两者都是一个跨平台的通用工具库，支持windows/linux/mac os,代码本身是c++写的，同时也有matlab，python，java，c/c++扩展接口，方便不同语言环境使用，可以说是科研和企业人员的首选！像我这样在学校的一般用matlab/c++，而我同学在百度则主要用的是python/c++，所以只是各自侧重不一样，但所使用的核心还是其svm库。

   以上Libsvm和Liblinear的主页上都有windows下的binary文件下载，zip,tar格式都有，解压后，找到matlab子文件目录，参看里面的readme文件，需要在matlab中进入此目录，运行make.m文件，matlab会根据本机默认的c/c++编译器将.c文件生成为.mexw32文件(由于我是32位操作系统，此处为mexw32,对于64位os，则对应为mexw64)，提供matlab下能使用的接口。之后生成了这些.mexw32文件复制到你自己的matlab工程根目录中，就可以在matlab文件中调用libsvm/liblinear库中的函数了~

http://blog.sina.com.cn/s/blog_5bd2cb260100ev25.html 这位网友对libsvm在matlab中的使用说明的很详细，可以参考下。

有关Liblinear和Libsvm各自的优势可以归纳如下：

1.libsvm用来就解决通用典型的分类问题

2.liblinear主要为大规模数据的线性模型设计

 

 

• it can be able to handle large-scaled dataset 可以用来处理大规模的数据
• it runs really faster than libsvm because it doesn't have to compute thekernel for any two points 由于采用线性核,所以不需要计算kernel value,速度更快
• trust region method for optimization looks new for machine learning people 

 

 

以下为一位网友采用liblinear进行数据分类的实验性能说明“

”今天试用了以下liblinear，速度很快（快到我没有想到）， 
我的实验数据： 
训练集：21504 * 1500（1500是样本的数量，21504是维度） 
测试集：21504 * 2985 
速度用秒来衡量，20次实验总共不到2分钟。 
 
同样的问题我用了libsvm实验速度上相差太大，libsvm实验5次，每次将近10分钟，时间是其次，发现一个问题就是，libsvm比liblinear的结果相差1个百分点，没有读liblinear的文章，不知道问题出在那个地方，libsvm我直接用的默认参数，线性模型。这样必然引起一个问题，如果我想评价线性模型和非线性模型的性能，我不可能一个用liblinear一个用libsvm,如果两个都用libsvm，报告的性能肯定有一些问题。 
 
所以如果你的问题维度很大（线性模型就有非常好的性能），不妨考虑liblinear. “

 

大致看了一下libsvm和liblinear的说明文档，发现一个问题就是在线性问题上两者的目标函数就不一样，所以性能上的差异是正常的，应该说如果优化同一样的目标函数两者性能应该会差不多，但是速度很明显，liblinear快很多。 
 
对于什么时候用线性模型的问题，我想上面的我举的例子用linear classifier就比较好，非线性分类不一定比线性分类器好，尤其是在样本及其有限，同时特征维度很高的情况下，因为样本有限的情况下，kernel map通常不准确，很有可能错误地划分类别空间，可能造成比线性模型更差的结果。 

 

说到scale，我建议不要用libsvm里自带的scale，因为一旦使用这个工具，它就会把原来稀疏的数据，变成非稀疏的格式，这样不但会生成非常大的数据文件，而且liblinear对稀疏数据快速处理的优势就不能体现出来了。因此，要scale，就自己写一个，以保持原来稀疏的格式

liblinear的好处就是速度快，尤其是对稀疏的特征。缺点就是太吃内存了。10G的数据量需要接近50G的内存，数据量再大就没法做了 。

另外，还有一个经常提到的svm库SVM-per：http://www.cs.cornell.edu/people/tj/svm_light/svm_perf.html 是康奈尔大学的人设计的。好像对计算机硬件的性能要求比liblinear要低...有做图像处理的人使用这个svm-per代替liblinear。

另外，对于多分类问题以及核函数的选取，以下经验规则可以借鉴：

 

• 如果如果特征数远远大于样本数的情况下,使用线性核就可以了.
• 如果特征数和样本数都很大,例如文档分类,一般使用线性核, LIBLINEAR比LIBSVM速度要快很多.
• 如果特征数远小于样本数,这种情况一般使用RBF.但是如果一定要用线性核,则选择LIBLINEAR较好,而且使用-s 2选项。

 

对于多分类问题：

对于15类场景来说，每类100幅训练图像，如果直接训练一个15类的multi-class classifier，则训练文件的Label值取1～15，wi标记不用指定（default 1）。如果对于每个类单独训练一个分类器，这样就把这个类的100幅图像作为正样本（假设Label=1），而其余所有的训练图像作为负样本（共1400幅，假设Label=-1），由此可以看出正负样本不平

原文地址：http://blog.sina.com.cn/s/blog_5b29caf7010127vh.html

liblinear VS libSVM

1. 关于trust region method:
trust region method是个优化的框架，a dual to line search。一般情况下，优化是个迭代的过程x_k+1 = x_k + alpha * p_k，其中p_k是方向，alpha是步长。在一般使用line search的优化中，先根据泰勒展式的局部模型计算p_k（就是在optimization里占大篇幅的各种方法的最速下降法、牛顿法、拟牛顿法等等），然后在确定p_k的情况下优化alpha，这一步就叫line search。trust region的思维恰恰相反，它是先确定一个region(hyperball)，或者说先确定它的半径delta（因为球心就是x_k），然后在此球内优化泰勒展式的局部模型（一般都是二阶）寻找方向p_k，如果优化成功则球心转移，并扩大半径；如果不成功则球心不变，缩小半径。并如此反复。
一个图文并茂的例子：http://www.applied-mathematics.net/optimization/optimizationIntro.html
wiki的介绍：http://en.wikipedia.org/wiki/Trust_region

2. truncated newton method
liblinear所用优化方法也是一种truncated newton method。truncated newton method是指牛顿法中计算H * p_k + g = 0时采用数值迭代解决这个线性系统问题而不是直接高斯消元，其中g和H分别是目标函数的一阶导和二阶导。通常情况下，这里可以用共轭梯度的近似解来逼近。
这里有篇综述，但是似乎不是很简单：http://iris.gmu.edu/~snash/nash/assets/TN_Survey/tn_survey.html

3. liblinear的l2-loss logistic regresssion and svm都是基于trust region newton method for large-scale logistic regression这篇论文的实现。文中的方法就是把1、2两点综合起来，具体可参阅文章。有两个有意思的地方，第一，文中将trust region newton和l-bfgs的复杂度进行了比较，直觉上l-bfgs应该要快一些，但是试验中却恰恰相反；第二，trust region引入了几个参数(sigma, lambda)，对于这些参数的取值作者说这都是经验的，不知道为什么在很多问题和数据下这就是最优的。具体的公式推导可以好好看文章，不管文章中的实验结果如何，liblinear的确已经得到界内广泛的认可了，今天的kddcup，这个研究组就用liblinear + feature engineering夺冠了。

liblinear的好处就是速度快，尤其是对稀疏的特征。缺点就是太吃内存了。10G的数据量需要接近50G的内存，数据量再大就没法做了
大数据量的可以用svmperf，也很快，耗内存少，精度嘛，不好比较。。

对于LibSVM:

何时使用线性核而非RBF核

■ 样本数远小于特征数

   例如生物学数据，70多个样本，7000多个特征

■ 样本数和特征数都很大

   例如文本分类，2万多样本，4万多特征

■ 样本数远大于特征数

   该情况作者并非推荐使用线性核，只是用来对比LibLinear和LibSVM的计算速度

文章来源： http://blog.sina.com.cn/s/blog_5b29caf701015ra0.html

LibShortText简要入门

LibShortText是一个开源的Python短文本（包括标题、短信、问题、句子等）分类工具包。它在LibLinear的基础上针对短文本进一步优化，主要特性有：

• 支持多分类
• 直接输入文本，无需做特征向量化的预处理
• 二元分词（Bigram），不去停顿词，不做词性过滤
• 基于线性核SVM分类器（参见SVM原理简介：最大间隔分类器），训练和测试的效率极高
• 提供了完整的API，用于特征分析和Bad Case检验

安装

下载并在解压后的目录下make就OK了。
注意：不支持Windows系统；Mac OS和Linux之间的库不通用

性能对比

关于LibShortText的性能，我们可以拿scikit-learn的朴素贝叶斯（参见用scikit-learn实现朴素贝叶斯分类器）和SVM（也是基于LibLinear）就前文提到的网页标题分类问题进行横向对比：

分类器	准确率	计算时间（秒）
scikit-learn(nb)	76.8%	134
scikit-learn(svm)	76.9%	121
libshorttext	79.6%	49

测试环境为低配版MBA2013

显然LibShortText无论在准确率和效率上都要更胜一筹。

API说明

虽然LibShortText提供了训练和测试的类命令行操作方式，但直接从Python脚本调用更加灵活和强大，了解和训练、预测和分析相关的API是有帮助的。

预处理

Converter模块负责将文本转化为数值化的数据集（数据格式与LibSVM相同），由于内置的分词器仅支持英文，如果要用于中文短文本的分类，就必须替换分词器（如下代码所示）。分词器是一个将文本转化为单词列表的函数，值得注意的是：分词器不会和模型一起保存，当重载模型时也必须重载分词器。

from libshorttext.libshorttext.converter import *

text_converter = Text2svmConverter()
text_converter.text_prep.tokenizer = comma_tokenizer
convert_text(train_file, text_converter, svm_file)

训练文本的格式如下：

娱乐\t组图：刘亦菲短裙秀腿 浓妆变冷艳时髦女

模型

LibShortText提供两组参数供训练时使用：

• train_arguments实际上是LibLinear的训练参数，可设定松弛参数C等
• feature_arguments是特征的表现形式，如词数、词频、TF-IDF等

预测

获得模型后，我们可以预测新文本的类别，LibShortText提供了两个API：

• predict_text(text_file, model) — 针对以行分隔的测试文本
• predict_single_text(single_text, model) — 针对单条文本

类别预测将返回一个PredictResult的对象，包含下列属性：

• predicted_y — 预测的类别（对单条文本预测时是字符串对象，对测试文本预测时是列表对象）
• decvals — 被预测文本对所有类别的决策变量，与文本到分类超平面的距离有关。它是一个列表而非字典对象，如果你希望和类别关联起来，可借助model的get_labels()：

decvals = zip(model.get_labels(), predict_result.decvals)

• true_y — 真实的类别（仅对测试文本预测时存在）
• get_accuracy() — 获得测试的准确率（仅对测试文本预测时存在）

分析

analyzer的作用是分析LibShortText的预测结果，通过它我们可以了解哪些特征更为关键、哪些类别容易被混淆。
比如分析一条体育新闻的标题：

analyzer = Analyzer(model)
analyzer.analyze_single('国青错失绝杀0-0韩国 下轮平越南就出线')

终端输出如下：

	sports	news	game	food	porn
……
国 青	4.600e-01	-1.349e-01	-4.283e-03	0.000e+00	0.000e+00
……
decval	1.192e+00	3.396e-01	3.132e-01	2.196e-01	1.910e-01

可见「国」和「青」一起促成最关键的sports类特征。
又比如，选择被误分的样本，调用gen_confusion_table()输出sports、star和movie的混淆表格，以了解哪些类别的特征界限比较模糊。

analyzer = Analyzer(model)
insts = InstanceSet(predict_result).select(wrong, with_labels(['sports', 'movie', 'star']))
analyzer.gen_confusion_table(insts)

终端输出如下（第一行表示预测类别，第一列表示真实类别）：

	star	movie	sports
star	0	19	5
movie	21	0	1
sports	15	4	0

完整demo请见lst_classifier.py。

文章来源：http://guoze.me/2014/09/25/libshorttext-introduction/