三角函数 [计算机数学专题(2)]
哈,明天就有一场考试。
考的内容也有三角函数,我们也想写一写 "用途多多的三角函数",
- 基本操作之地球周长
- 基本操作之地月距离
- 基本操作之恒星距离
- 基本操作之太阳地球间的距离
- 计算机新闻分类
- IT起源学说:e = 2.71828...
- 最美的数学公式
- 傅里叶变换
《目录》
- y = sin (x)
- y = cos(x)
- 弧度制
- 地球周长
- 地月距离
- 恒星距离
- 太阳地球间的距离
- 计算机新闻分类
- IT起源学说:e = 2.71828...
- 复数
- 陌生的指数
- 最美的数学公式
- 傅里叶变换
希望,我们能写的有趣和准确。
咳咳,为什么是我们 ?是自我的精神分裂:
自我1: 三角函数多用于工程上。
自我2: 的确,毕竟三角函数公式那么多,不过都是类似加减计算一样简单, 但记的我好郁闷。
自我1: 哈!?? 你是记的 ??我不记公式的,多写几遍就理解了。
自我2: 切,你那是被公式给唬住了。
......
自我1: 反正,三角函数这个东西,即简单又易懂。可是被你学杂了。
自我2: 一边去,我看你也就是知道逻辑,并没有理解内在!
自我1: 好,好,好,这样吧!!
物理学家费曼说:"如果你不能用简单的语言给一个外行解释一个东西,你就是没有真正理解这个东西"。
不需要我说了吧,赶紧去找幼儿园的小朋友,看谁可以让ta听懂三角函数。
自我2: who 怕 who,就是当着全宇宙的小朋友面,我也能讲懂 ! !
自我3: 不用找了,你们俩个不就是吗 ?
自我1,自我2 :0.0 ...... 0.0
听说,如果我们做的是不该做的事,内心就会有一些压力,ta就会发出禁止的声音。
从单位圆开始,单位圆是半径为 1 的圆,现在试着画一个单位圆。
用 Python 画出来。资料: turtle 、turtle官方文档
-
import turtle # 导入画画模块 turtle.showturtle() # 显示窗口 turtle.write(" 0 ", font = ("华为琥珀", 20 , "normal")) turtle.goto(200,0) # 向 x 轴正方向前进 100,y 不变 turtle.write("x", font = ("华为琥珀", 20 , "normal")) # 打印文字 turtle.goto(-200,0) # 向 x 轴负方向前进 100 , y不变 turtle.penup() # 提笔 turtle.goto(0,200) # 画 y 轴的坐标,因为提笔了所以没有画线 turtle.write("y", font = ("华为琥珀", 20 , "normal")) turtle.pendown() # 落笔 turtle.goto(0,-200) turtle.goto(0,-100) # 到坐标轴中心画圆 turtle.circle(100) turtle.write(" r = 1", font = ("华为琥珀", 20 , "normal")) turtle.done() # 保留窗口
假设 有一点,在圆上运动,记为P。
我们要研究P点运动时在圆的不同位置和 y 轴有什么关系,那么以什么标准研究好呢 ?
P 一直变化,ta的坐标也会一直变化,那就研究 ta产生的角度吧。
连接OP,与OX构成 ![]() ,这是一个随P运动而改变的角度。
,这是一个随P运动而改变的角度。
研究坐标与角度的关系:点 P 轴单位圆做圆周运动时 ,
![]() 与 y 轴的关系是怎样 ?
与 y 轴的关系是怎样 ?
![]() 与 x 轴的关系是怎样 ?
与 x 轴的关系是怎样 ?
y = sin (x)
如果把 ![]() 与 y 轴的关系 对应为函数。函数自变量 x 是角度,函数因变量 y 是 P 的 y坐标。
与 y 轴的关系 对应为函数。函数自变量 x 是角度,函数因变量 y 是 P 的 y坐标。
这个对应法则记为 sin,写法如下,
- y = sin (x),x 是 角度。
当 x = 0º,点 P 就在 x 正半轴上, sin (0º) = 0
当 x = 90º, 点 P 也正好在 y 正半轴上, sin(90º) = 1
现在 P 点转了一圈,那么 ta 运动范围可达到的极限是 -1 到 1,即函数 y = sin(x) ,y 的值域是 [-1, 1]。
对呀,在坐标轴上圆的半径是 1 ,P 在单位圆活动距离中 y 最大分别是,当 P 在 90º 和 270º。
不过,我们研究的是 坐标与角度的关系,距离是正数,在表示负下标时如 sin ( 270º ) ,要写成 负数,sin(270º) = -1。
所以,试试 sin(180º) 和 sin(360º) ...
"都是0、都是0",我猜小朋友能答对的。(如果这句话伤害到了您,我只能表示惬意~)
那 sin(45º) 是 sin(90º) 的一半是吗 ?
看看函数图像就明显了,sin(45º) 图像,
对比 y 轴,连接 y-P 的虚线显然要大于 1 的一半, 所以 sin(45º) 并不是 sin(90º) 的一半。
这是由俩个等边直角三角形组成的正方形,我们可以用 勾股定理 or 正方形对角线 计算出 PH 即sin(45º)。
勾股定理:研究的是直角三角形三边的关系 ![]() ,应该不陌生。
,应该不陌生。
![]()
![]()
![]()
![]()
那么,您能画图分析并计算出 sin(60º) 吗,可做辅助线。
这些都是三角函数的特殊特殊角,
看 sin 时,我发现 60 和 120 都是 ![]() , 这是为什么 ?
, 这是为什么 ?
哈哈,回想 P 点的图像,就会发现在 这俩个角度,P的 y 坐标并没有变化,只是 x 坐标变了,
那么,同理推出更多相似的角,
60º 和 120º 和 240º 和 300º 是相似的,超过 180º 的是负数。
如果把 sin(0º) 到 sin(360º) 的点连起来,在坐标轴上长啥样 ?
| sin | 分数形式 | 小数形式 |
| sin(0º) | 0 | 0.0 |
| sin(30º) | |
0.500··· |
| sin(45º) | 0.707··· | |
| sin(60º) | 0.866··· | |
| sin(90º) | 1 | 1.0 |
| 其ta象限都是对称角 | \ | \ |
看坐标轴的横坐标竟然不是 x ?
三角函数的正弦曲线研究的是 y 和 P 运动的角度 的关系,一般把 P 运动的角度记为希腊字母 ![]() (读西塔,也是渐进记号的读法)。
(读西塔,也是渐进记号的读法)。
y = cos(x)
那么, ![]() 与 x 轴的关系是怎样 ?
与 x 轴的关系是怎样 ?
相信您看了sin已经知道个大概,就不在复述,因为还有一个更重要的知识呢 --- 弧度制。
弧度制
用( º )的单位表示角,是角度制,1º 等于 周角的 ![]() 。
。
弧度制是由大数学家欧拉提出,长度等于半径长的弧所对的圆心角记为 1 弧度(rad),其核心:圆弧的长度是半径的多少倍。
我们知道了一些常用的角度与弧度的对应值,
| 角度 | 弧度 |
| 1º | |
| 90º | |
| 180º | |
| 360º |
举个例子,360º
360º时,P 刚好落在 x 轴上。
半径为 r 的圆的圆周 = 2 * 圆周率 * 半径,![]() ...
...
弧度制核心:圆弧的长度是半径的多少倍
90º 是 360º 的 四分之一, 60º 是 360º 的 六分之一 ,试着计算 90º 、60º 是多少弧度(rad) !
做另一个三角形,使勾股定理成立,这一步我省略了尝试自己推出来,最后得出 :![]() 。
。
哦,对了。角 ![]() 的弧度公式是
的弧度公式是 ![]() , l : 角
, l : 角 ![]() 对应的弧长, r :圆半径。
对应的弧长, r :圆半径。
地球周长
引言: 亚里士多德在其著作中记述了很多地球是圆形的证据,于是就有许多学者想要知道地球的周长是多少 !
回忆圆的周长公式 : ![]() , 只有地球半径是不知道的。
, 只有地球半径是不知道的。
![]() 知道地球半径即可~
知道地球半径即可~
不要百度?半径因为今天主角是数学...
数学史上,俩次数学高峰期第一次就在古希腊,让我们一起回到那个数学史上了不起的年代吧。
地球周长最早是被古希腊学者兼亚历山大图书馆第三任馆长所记录 --- ta叫埃拉托斯特尼 简称 埃尼吧。
埃尼 从书中便知道每年的6月21日,阳光在正午时会直射 (光线和地面是直角) 到埃及的阿斯旺水井中。
p.s. 因为阿斯旺处于北回归线上,阳光会在夏至时直射北回归线。
于是,埃尼测量了6月21日当天的亚历山大,阳光在正午时射入水井中的角度为 7º 12''。
接着,从旅行的商队那里得知了亚历山大与阿斯旺之间的近似距离,这是角 ![]() 对应的弧长 。
对应的弧长 。
按照上图分析,照射给亚历山大与阿斯旺的太阳光是平行的。
所以,亚历山大和阿斯旺之间的夹角也等于 7º 12''。
而亚历山大已经从商队知道了弧长 L ,因此我们转换公式为求半径 : ![]()
最后把弧长L代入便估算了地球的周长是 39, 690公理,与今天的 40,076公理只有 2% 的误差。
总结:计算地球周长,结合一个圆以圆上的一个弧度和角度,求出ta的半径再代入 圆的周长公式 : ![]() 即可。
即可。
地月距离
古希腊学者再计算出地球周长之后。又在这个基础上琢磨地球和月亮的距离了,我们一起回到那个搞事情 NX 的年代吧。
前置技能:圆形的阴影。
圆形的阴影:一个圆形的物体经过光的照射后会有一个圆形的阴影。随着物体的不断升高,阴影会渐渐变成一个 ▪️ 黑点。这个黑点到圆形物体的距离刚好是物体直径的 108 倍,地球?也是如此,可以用手电筒?代替太阳模拟。
古希腊学者,以这个规律来研究地月距离。说到月球,不得不说一个特殊现象 --- 天狗食月。
天狗食月,是因为地球夹在太阳和月亮之间,挡住了供给月球的太阳光导致看月亮好像是被咬了。
当月球不断运动经过地球产生的阴影区时,古希腊学者估算出月球通过面前这段阴影区(FE)长度大概是月球直径(ED)的 2.5 倍。
数学表达: FE = 2.5ED
为方便分析,古希腊学者又建立了数学模型,
这样就产生了 3 个三角形,刷题的经验告诉了我们,这就是求出地月距离的关键。
ta们分别是 ABC、AFE、CDE ...
三角形求高的公式:h=2×S△÷a(S△是三角形的面积,a是三角形的底)
思考 3 min...
从小到大,依次分析:
最小的三角形 CDE,ta的高就是 地月之间的距离,ta的底是 月亮的直径。
次大的三角形 AFE,ta的高是 FE * 到月球的距离,ta的底是 FE = 2.5ED。
最大的三角形 ABC,ta的高是 108*BC(根据圆形阴影理论),ta的底是 BC(地球直径)。
因为三角形 ![]() ,比例关系为 2.5。所以俩个三角形高的比例也是 2.5。
,比例关系为 2.5。所以俩个三角形高的比例也是 2.5。
p.s. 如果两个图形形状相同,但大小不一定相等,那么这两个图形相似(相似的符号:∽)。
把AFE三角形的高记为 AH(H点需要自己标注),CDE三角形的高设为 x ,则 AH = 2.5x。
三角形 ABC的高记为 AG,G点需要自己标注上去。
那么从H点到G点也是地月间的距离,因此 HG = x。
推出 :2.5x + x = AH + HG = AG,又因为 AG 是三角形 ABC 的高等于 108 * 地球的直径(记为d)。
![]()
![]()
埃尼计算出来的地球半径为 39, 690 ,古希腊学者们取了近似值 40, 000,那么地球直径为 d = r * 2 = 40, 000 * 2 = 80, 000。
代入公式即 ![]() 英里,这就是古希腊学者计算的地球距离,与今天计算的 239, 000 英里相差也不大。
英里,这就是古希腊学者计算的地球距离,与今天计算的 239, 000 英里相差也不大。
后来,法国学者运用三角函数(另三角学方法)也解出来,因为三角函数本就源于天文学......
恒星距离
计算恒星距离非常方便,因为只需要眼睛、鼻子、手指,电影里面水手也经常会用视差法。
p.s. 只适合度量 300 光年以内的恒星距离。
做实验:
如果把右手食指(竖起来)紧贴着鼻子的中间,现在俩只眼睛看手指,这时的食指是处于左右眼间。
如果闭上左眼看食指,食指会在右边一点;如果闭上右眼看食指,食指会在左边一点。
实验? ......
食指与俩只眼睛?之间的夹角,称为视差;
俩只眼睛?之间的距离,称为基线;
我们再一般化视差、基线这俩个概念,等下好用于计算恒星距离。
基线:有一定距离的俩个点(?) 之间的距离。
视差:从有一定距离的俩个点(?) 上同时观察一个目标(☝️) 产生的方向差异。
视差角:从目标看俩个点之间的夹角。
安利小知识:知道视差角和基线就可以计算出目标和点之间的距离。
推理上面小知识的连环画:
我们现在需要求出 h ,要怎么搞 ??
有点抱歉,三角函数的 tan 函数我还没讲,那简单介绍一下吧。
![]() ,
,![]() 是角度这个不用解释, a 是
是角度这个不用解释, a 是 ![]() 的对边, b 是
的对边, b 是 ![]() 的邻边。
的邻边。
举一个现成的例子,以上图的 ![]() 以为例。
以为例。
推一下公式,变成求 h 的:
![]()
好,这样就求出目标(食指)到点(眼睛)的距离。
看着这图(新图),目标就是恒星,点就是地球和 6 个月后的地球。
恒星与太阳的距离就是 点到目标的距离(d) ,求出 d 只需要知道 P 这个角度是多少 !
至于地球和 6 个月后的地球的距离也就是基线,是地球椭圆轨道长轴的一半记为 a。
p 需要计算得出,a 是以知,这样就可得出 d,恒星的距离就计算出来啦。
- 半长轴就是椭圆中离中心最远的点。
- 对于地球公转轨道来说,就是地球的远日点距离。
- 地球在远日点时,与太阳的距离是152,097,701.0千米,或是约1.521亿千米。
太阳地球间的距离
这张图,就是我们突破计算的关键,普及一点 太阳、地球、月亮 的关系。
每年每月的农历初一,月球正在太阳和地球中间(上图中,月球会在 斜线S 上),这时候的月亮无法看到因为地球看到的月球是没有光的背面。
随着月球的运动,月球逐渐挪开了,这时候从地球(西方才能看到)看到的月球是弯弯的勾月......
在农历初八时,从地球(东方可见前半夜)看的月亮是明亮的半面,如上面这样、几何图形是上上图那样 -- 直角三角形。
到农历十五、十六时,月亮已经运动到与太阳呈 180º。这时候从地球看到的月亮是完全的因为看到的是月球受光的一面。
这 4 个阶段,分别被称为 "新月"、"峨眉月"、"上弦"、"满月",如此反复 满中逝,逝中满......
日中则移,水满则溢,月盈则亏,这是自然界的铁律。
求的太阳与地球的距离,也就是斜线 S,而 L (地月距离)古希腊学者已经计算出来,所以以知。
![]()
我们现在只需要知道 ![]() 这个角度是多少即可求出 S ~
这个角度是多少即可求出 S ~
阿里(阿里斯塔克斯) 虽然不知道 "上弦" 月出现的正确时间,依然计算出 ![]() = 87º (实际是 89.853º)。
= 87º (实际是 89.853º)。
![]()
阿里的得出一个不确定结果 S: 地月距离的 20 倍。
实际上:地月距离的 390 倍,大概是 15 亿公里......
计算机新闻分类
现在浏览器上的新闻,都是计算机自动分类的。
计算机分类的原理是三角函数的余弦定理 + 向量。
余弦,我们已经知道一点点,更多的知识需要您自己学习,而向量是多维空间中有方向和特定长度的量。
原理 : 余弦定理可以只靠俩个三角形的俩个边的向量,计算出这俩个边的夹角。
一篇新闻里会有很多词,像 “之乎者也的” 这种虚词,对判断新闻的分类没有太大的意义。而像 “股票”、“利息” 这种实词,是判断新闻分类的重点词。科学家精选了一个词汇表,这里面收录着 64000 个词,每个词都对应一个编号。他们先把大量文字数据输入计算机,算出每个词出现的次数。
一般出现次数越少的词越有搜索价值,比如 “爱因斯坦”、“数学之美”;而出现次数越多的词,越没有搜索价值,比如“一个”、“这里” 等等。根据这个标准,把词汇表里的64000个词都算出各自的权重,越特殊的词权重越大。然后,再往计算机里输入要分类的新闻,计算出这64000个词在这篇新闻里的分布,如果某些词没有在这篇新闻里出现,对应的值就是零,如果出现,对应的值就是这个词的权重。这样,这64000个数,就构成了一个64000维的向量,我们就用这个向量来代表这篇新闻,把ta叫做这篇新闻的特征向量。
不同类型的新闻,用词上有不同的特点,比如金融类新闻就经常出现 “股票”、“银行” 这些词,所以不难判断,同类新闻的特征向量会有相似性。
只要算出不同新闻特征向量之间夹角的大小,就可以判断出是不是同一类新闻。这时就要用到余弦定理,来把两则新闻的特征向量之间的夹角算出来。科学家可以人工设定一个值,只要两个向量之间的夹角小于这个值,这两则新闻就可以判定成同一类新闻。
余弦定理:对于任意三角形ABC,已知两条边的边长分别为a和b,两边的夹角为C,则第三边的边长满足下列等式:
在向量中公式转换为:
把公式翻译为代码:
double CosSimilarity(double *va, double *vb, int vn)
{
double cossu = 0.0;
double cossda = 0.0;
double cossdb = 0.0;
for (int i = 0; i < vn; i++)
{
cossu += va[i] * vb[i];
cossda += va[i] * va[i];
cossdb += vb[i] * vb[i];
}
return cossu / (sqrt(cossda) * sqrt(cossdb));
}vn 是多少维,也就是词典中有多少个词。
完整代码:
#include
#include
double CosSimilarity(double *va, double *vb, int vn)
{
double cossu = 0.0;
double cossda = 0.0;
double cossdb = 0.0;
for (int i = 0; i < vn; i++)
{
cossu += va[i] * vb[i];
cossda += va[i] * va[i];
cossdb += vb[i] * vb[i];
}
return cossu / (sqrt(cossda) * sqrt(cossdb));
}
// 建立的词典
const int VN = 11; // 11 个词即 11维
const char *base_words[] =
{
"进攻", "炮弹", "射程", "榴弹炮", "发射", "口径", "迫击炮", "瞄准", "后坐力", "弹道", "目标"
};
/* 原文 */
//第一行: 口径为155毫米的榴弹炮,炮弹的射程超过40公里,炮弹发射后击中目标的弹道是一条抛物线
//第二行: 大口径榴弹炮射程很远且弹道弯曲,炮弹通常都不是直接对着目标瞄准,而是计算好抛物线弹道,以一定的仰角和方向发射炮弹
//第三行: 我们必须统一口径,抵挡敌人发射的糖衣炮弹的进攻
int main()
{
// v1代表原文第一行的 11 个关键字出现的权重(一一对应, 出现n次权重为n)
double v1[] = { 0, 2, 1, 1, 1, 1, 0, 0, 0, 1, 1 };
double v2[] = { 0, 2, 1, 1, 1, 1, 0, 1, 0, 2, 1 };
double v3[] = { 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0 };
/* 检查相似度 */
printf("第一行 和 第二行 的相似度: %.2lf\n", CosSimilarity(v1, v2, VN));
printf("第一行 和 第三行 的相似度: %.2lf\n", CosSimilarity(v1, v3, VN));
printf("第二行 和 第三行 的相似度: %.2lf\n", CosSimilarity(v2, v3, VN));
return 0;
} 代码还可补充,当相似度大于设定值时,归为一类新闻......
IT起源学说:e = 2.71828...
自然常数 e , 是一个无限不循环的小数,也是最能体现自然界特征的数。
e 的出现,连接起三角函数与指数函数。
如果 e 不精确的等于 2.71828... ,绝大多的积分变化就会失效。
计算机的信息技术基础便是源于傅里叶、拉普拉斯、希尔伯特等变化开始的,IT产业的起源所在。
举个例子:理解 e
- 您在银行存了 1 块钱,银行给您非常高的利息,年利率是100%,这样过一年存款就变成了 2¥。
- 但银行非常慷慨,可以半年付一次利息,那肯定比一年付一次赚得更多。
- 那到底半年付一次利息能赚多少钱呢,是 2.25¥。
- 您就觉得非常划算了,就要求银行按季度来付利息,这样算出来是 2.37¥。
- 如果您要求更密集一些,按月来付利息,每月付年利息的
,那么年底能拿到 2.61¥。
- 发现只要支付利息的间隔越短,收益就越高。
- 那现在按天来支付利息,算出来就是2.714567¥。
- 我们推到极致,按秒来付利息,那这个收益会大到什么程度呢 ?
- 无限切分,这样最终的收益不是无限大的,而是无限趋近于一个数值,自然常数 e,收益就是 2.71828¥。
大约 2.718 倍的收益率,背后的实质是增长的极限,ta还可以出现在任何有裂变式增长的情境下。如微生物繁殖 ......
这是一个宇宙通用数:如果存在外星文明,那么ta们的数学也会有一个描述宇宙自然规律的数,类似我们的 e = 2.71828...
因为文明是贴切于生活的,工具的发明是针对问题的,数学也可以理解为人类文明持续发展的工具之一,
- 为计算数字,发明了算盘;
- 为测量绝对的数值,发明了尺子、时钟、天平、称;
- 为测量化学反应的当量,发明了有刻度的量器;
- 为让计算机快速完成判断真假、比较大小、排序、挑选最值,发明了二叉树。
而 e ,比ta们都重要,ta是宇宙本身,谁都比不上 e,如果 e 不等于 2.71828... , 也许就不会有宇宙,更不会有我们了 。
复数
从最基本的概念出发,推导出复数这个东东。
首先,对这个东东我也是不了解,数学啥时候出来一个复数,没听说过。
诶,想数学最早起源于计数吧,著名的:结绳计数。
于是有了 1、2、3、4、5、6、7、9···,之后有了【加法】,为了分别计算又冒出一个分别参与运算的 0,自此【自然数】渐渐被整个人类所接受。
有了加法后,又想到加法的逆运算【减法】,自然数并不完备,慢慢又推导出了【负数】,自此由自然数变成了【整数】。
为了加速计算加法,【乘法】便诞生了,不过俩个整数相乘还是整数......
有了乘法的概念,乘法的逆运算【除法】又自然而然的诞生,因为有时候除出来的商不是整数,因此出现了【有理数】。
有了乘法,冒出了 "平方" 的概念(自己乘自己),后来又想到了 平方的逆运算 【开方】。
对 2 开方是什么东西,于是在有理数的基础上扩充为【无理数】,现在整个数系叫【实数】......
开方对正数来说,数系是完备的,但对 -1 开方又是什么东西,没有一个实数平方等于 -1 ,于是数系添了【虚数】......
让新定义【虚数】的平方等于 -1,这就是 i,即 ![]() 。
。
所以,整个数系,由是实数和虚数组成,叫复数,有了复数,加减乘除、平方开方,都完备。
复数的基础虽然在自然界没有对应的事物,但建立在不存在的基础上的工具解决了许许多多的现实问题,如电磁波。
用数学研究数学 >> 在几何上表示复数...
实数轴:是一种特定几何图形;原点、正方向、单位长度称数轴的三要素,这三者缺一不可。
虚数轴: 对应平面上的纵轴,与对应平面上横轴的实数同样真实。
![]()
复平面: 虚数轴和实数轴构成的平面,复平面上每一点对应着一个复数。
陌生的指数
指数,我还没接受过来。
![]()
也许,常年的解题经验告诉您 :指数是多少,就是多少个 10 相乘。
的确是的,不过只在指数是自然数时。指数的法则才是上面那样,如果指数是这样的呢 ?
![]()
是不是 ![]() 个 e 相乘呢 ?
个 e 相乘呢 ?
不、不是,绝对不是。
当指数不是自然数时,不用 "乘以的个数" 来思考指数,而是用数学公式来定义。
定义思维,是研究数学最珍贵的。具体的介绍可以参见:集合论
定义的 ![]() 要满足 3 条指数法则:
要满足 3 条指数法则:
![]()
![]()
![]()
这种 "无矛盾性" 的定义才是数学的基石,举个例子,也许您不知道 ![]() ?
?
研究一下式子,
![]()
![]()
![]()
![]()
![]()
![]()
发现指数每减 1 ,结果减缩小了 ![]() 。所以,
。所以,![]() 也是这样定义出来的 ?
也是这样定义出来的 ?
自然数的确可以这样推,不过这还不是正确的定义。
![]()
![]()
![]()
![]()
![]()
发现对于指数法则的前 2 条都对应了,我带进了第 3 条,结果。
啊哈,没毛病。
最美的数学公式
![]() :单位圆上,幅角为
:单位圆上,幅角为 ![]() 的复数等于 -1。
的复数等于 -1。
为了理解欧拉的公式,从 ![]() 的微分方程来表达指数函数。
的微分方程来表达指数函数。
求微分是从函数创造函数的方法,可能不明所以,任何函数都可以转换为幂级数的形式表达包括指数函数。
![]()
![]() 是 x 的 0 次方项,系数为
是 x 的 0 次方项,系数为 ![]() ;
;
![]() 是 x 的 1 次方项,系数为
是 x 的 1 次方项,系数为 ![]() ;
;
![]() 是 x 的 2 次方项,系数为
是 x 的 2 次方项,系数为 ![]() ;
;
把这些项相加,得到的式子称为 幂级数,再把 指数函数的幂级数 表达为微分的形式。
' 符号涉及微分,需要考虑俩条法则:
- 常数的微分结果等于 0,(a)' = 0;
- n 次方项的微分结果等于
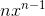 ,
,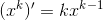 ;
;
指数函数的幂级数: ![]()
以上面的形式求微分:![]()
分解右边的式子: ![]()
因为微分是从函数中创造函数,这俩个函数其实是相等只是表达的形式不同。
![]()
分别展开:
![]()
![]()
![]()
![]() =
= ![]()
比较等式俩边 x 的各项的系数:
-
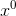 :
: 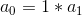
-
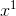 :
: 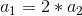
-
 :
: 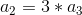
-

- ······
-
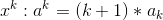
感觉规律还不明显,那把公式变成分数形式:
这样使之成为了一个数列,只需要知道 ![]() 就可得到整个数列的值。
就可得到整个数列的值。
现在想想 ![]() 是多少 ?
是多少 ?
回顾关于 ![]() 有关的式子,
有关的式子,
![]() ,
, ![]()
![]()
当 x = 0 时, ![]() 。把 x = 0 代入到
。把 x = 0 代入到 ![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
知道 ![]() 就可以得到之前的数列了。
就可以得到之前的数列了。
![]()
![]()
这个式子是泰勒展开,专业名字叫,
而学习的式子,TA的指数是 ![]() ,把TA们代入 指数函数
,把TA们代入 指数函数 ![]() 的泰勒展开试一试:
的泰勒展开试一试:
复数的知识上面有记录,![]()
根据虚数 i 的性质,式子变化的规律:
得说一件事情,![]() 是欧拉推来出的。
是欧拉推来出的。
那么欧拉推过来之前的 e 的指数是什么 ?
实际只是一个希腊字母 ![]() ,表示任意角度。
,表示任意角度。
![]() 才是原来的样子。
才是原来的样子。
各位知不知道 sin(![]() ) 和 cos(
) 和 cos(![]() ) 的泰勒展开 ?
) 的泰勒展开 ?
泰勒展开资料:https://en.wikipedia.org/wiki/Taylor_series ,需要VPN没有可以找我。
把 ![]() 的泰勒展开以奇次项和偶数项分开,发现偶数项对应的是
的泰勒展开以奇次项和偶数项分开,发现偶数项对应的是 ![]() 的泰勒展开,奇次项对应的
的泰勒展开,奇次项对应的 ![]() 的泰勒展开。
的泰勒展开。
哦哦,感觉好神奇!
诶,不对奇次项还少乘一个 i,我们补上 i 再写成等式。
![]()
接着代入 ![]() ,
, ![]() 的泰勒展开:
的泰勒展开:
![]()
三角函数的博客,记录了cos和sin的求值方法这里不在复述。
![]()
![]()
傅里叶变换(FT)
十九世纪法国数学家 傅里叶 发现任何周期性的函数(信号)都等同一些三角函数的线性组合。
简单的来说,傅里叶变换是把一个复杂的事物拆解为一堆标准化的简单事物的方法。
如,跳舞这个复杂的动作由腿部、手部、肩部、腰部等单一的动作组成。
举一个相关的例子,傅里叶运用于声音中。
声音是空气的震动,手指轻轻地弹一下碗,我们会听到 悦耳的声音。
声音由 音调 和 音量(响度) 组成,音调是震动的频率,音量是震动的幅度。
上图的正弦曲线,也是一个简单的声音。
这个声音呈完美周期性的变换、频率是固定的。
而一个复杂的声音,就是由这样简单的声音组成。
因此,傅里叶变换在声音的领域中即:
由一系列简单的波动如搭积木一般组成一个复杂的波动,看下图。
![]()
图中俩条红色的曲线,都是由那些蓝色的波形叠加而出。
傅里叶变换最核心的是可以告诉我们,图中红色曲线是由多少组成比例的蓝色曲线构成。
红色曲线 = 频率是 100 的蓝色曲线 × 0.5 + 频率是 200 的蓝色曲线 × 0.2 + 频率是 300 的蓝色曲线 × 0.1 + 频率是 400 的蓝色曲线 × 0.08 + ……
取出蓝色曲线的数值成分:红色曲线 = (0.5, 0.2, 0.1, 0.08, ......)。
写一篇文章,会参考许多资料;那这篇文章,就可以拆分为 《XX》*0.1 + 《XX》*0.2 + ......
所以,现在大部分原创经常是已知的、简单的事物的排列组合。
这里说的是,傅里叶变换的思想原理,而其中更加有趣的地方,您可以看看:
- 《傅里叶变换的终极解释》(上)
- 《傅里叶变换的终极解释》(下)
- 《用傅里叶变换画出任何简笔画》
另外推荐:
- https://www.algorithm-archive.org/contents/cooley_tukey/cooley_tukey.html
- https://betterexplained.com/articles/an-interactive-guide-to-the-fourier-transform/
快速傅里叶变换(FFT),在算法竞赛中多用于求 "卷积"(多项式乘法),朴素的卷积各系数相乘的时间复杂度是 ![]() ,通过 FFT 后减为
,通过 FFT 后减为 ![]() 。
。
![三角函数 [计算机数学专题(2)]_第1张图片](http://img.e-com-net.com/image/info8/8cec25cada7f40ffbc46ea3e7ebe237e.jpg)
![三角函数 [计算机数学专题(2)]_第2张图片](http://img.e-com-net.com/image/info8/5aca367594bc4479bf868d2035328946.jpg)
![三角函数 [计算机数学专题(2)]_第3张图片](http://img.e-com-net.com/image/info8/29a38d5f2d654d1bb930c1f388eebc4f.jpg)
![三角函数 [计算机数学专题(2)]_第4张图片](http://img.e-com-net.com/image/info8/fb958edef74c4734a2aaa53b304bed87.gif)
![三角函数 [计算机数学专题(2)]_第5张图片](http://img.e-com-net.com/image/info8/64e1ebb75ffb4c33b9eb11392d7c24ac.jpg)
![三角函数 [计算机数学专题(2)]_第6张图片](http://img.e-com-net.com/image/info8/94f42c0b439147bca2d1d4cc045efabd.jpg)
![三角函数 [计算机数学专题(2)]_第7张图片](http://img.e-com-net.com/image/info8/56bcecab83384919824f35054138d113.jpg)
![三角函数 [计算机数学专题(2)]_第8张图片](http://img.e-com-net.com/image/info8/41631cbe68b042c08f22cd0ccc636346.jpg)
![三角函数 [计算机数学专题(2)]_第9张图片](http://img.e-com-net.com/image/info8/5b7eb44c4c5f4f9f8e67d9f7f73533cf.jpg)
![三角函数 [计算机数学专题(2)]_第10张图片](http://img.e-com-net.com/image/info8/7d9086d1abe94df09c19d11ea2e59561.jpg)
![三角函数 [计算机数学专题(2)]_第11张图片](http://img.e-com-net.com/image/info8/39aecceafcfc4f6599771448b64e9085.jpg)
![三角函数 [计算机数学专题(2)]_第12张图片](http://img.e-com-net.com/image/info8/7a99cf815b144e9fa140d376a75c0714.gif)
![三角函数 [计算机数学专题(2)]_第13张图片](http://img.e-com-net.com/image/info8/dc1b9315545d4d519df5c79b7175097b.jpg)

![三角函数 [计算机数学专题(2)]_第14张图片](http://img.e-com-net.com/image/info8/2bff97a8945f48bdbf8f99fe5e3502b6.jpg)
![三角函数 [计算机数学专题(2)]_第15张图片](http://img.e-com-net.com/image/info8/5e7ed6c275a7459ebed705c800d74b1c.jpg)
![三角函数 [计算机数学专题(2)]_第16张图片](http://img.e-com-net.com/image/info8/f8d5e9f9f9ee4a5d8d29c569c8026f4c.jpg)
![三角函数 [计算机数学专题(2)]_第17张图片](http://img.e-com-net.com/image/info8/e7843ab8a21a4bdb9a11b518a7335754.jpg)
![三角函数 [计算机数学专题(2)]_第18张图片](http://img.e-com-net.com/image/info8/ef256a1280ed4229b10fea442a92957f.jpg)
![三角函数 [计算机数学专题(2)]_第19张图片](http://img.e-com-net.com/image/info8/cb062ac23ad547a289a0e126800dd668.jpg)
![三角函数 [计算机数学专题(2)]_第20张图片](http://img.e-com-net.com/image/info8/54a7af9f4d3c47679ffc197285e087f7.jpg)
![三角函数 [计算机数学专题(2)]_第21张图片](http://img.e-com-net.com/image/info8/bc053b2d68224d2689258b97fa3b69f6.jpg)
![三角函数 [计算机数学专题(2)]_第22张图片](http://img.e-com-net.com/image/info8/f41af1fdf9cd491081472881aca9f8e8.jpg)
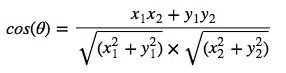
![三角函数 [计算机数学专题(2)]_第23张图片](http://img.e-com-net.com/image/info8/711fc464aa184368bac0f381306e495c.jpg)
![三角函数 [计算机数学专题(2)]_第24张图片](http://img.e-com-net.com/image/info8/6f9a01c0884f48dab27a1f7bedbd2db4.jpg)
![三角函数 [计算机数学专题(2)]_第25张图片](http://img.e-com-net.com/image/info8/af73283f1a034fa29f1cb85b984b2e92.jpg)
![三角函数 [计算机数学专题(2)]_第26张图片](http://img.e-com-net.com/image/info8/b08da79a146e4f90b0b172b4f1bf983b.jpg)

![三角函数 [计算机数学专题(2)]_第27张图片](http://img.e-com-net.com/image/info8/39c8dffbce164c1b80db42f326d27c84.jpg)

![三角函数 [计算机数学专题(2)]_第28张图片](http://img.e-com-net.com/image/info8/8051dc13187b4aaca337da56641bbfe2.jpg)
![三角函数 [计算机数学专题(2)]_第29张图片](http://img.e-com-net.com/image/info8/a0ab2d6b23e34450ab4fe0fb44e7f1d4.jpg)
![三角函数 [计算机数学专题(2)]_第30张图片](http://img.e-com-net.com/image/info8/b0bece4aa9a24f3295e106c2baf758e1.jpg)