(详细)后缀数组模板及简单的入门题总结
数据结构SA
打算把有意思的SA解法写下来!!!
接下来是SA数组的板子以及Height最长公共前缀
const int maxn = 2e5+5;//开总串长度,不要忘记连接符
int wa[maxn],wb[maxn],wsf[maxn],wv[maxn],sa[maxn];
int Rank[maxn],height[maxn],s[maxn];
char str1[maxn],str2[maxn];
//sa:字典序中排第i位的起始位置在str中第sa[i] sa[1~n]为有效值
//rank:就是str第i个位置的后缀是在字典序排第几 rank[0~n-1]为有效值
//height:字典序排i和i-1的后缀的最长公共前缀 height[2~n]为有效值,第二个到最后一个
// sa数组的范围是0~n-1
int cmp(int *r,int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
}
void getsa(int *r,int *sa,int n,int m)//n为添加0后的总长
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0; i=0; i--) sa[--wsf[x[i]]]=i;
p=1;
j=1;
for(; p<=n; j*=2,m=p) //倍增的算法
{
for(p=0,i=n+1-j; i<=n; i++) y[p++]=i;
for(i=0; i<=n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0; i<=n; i++) wv[i]=x[y[i]];
for(i=0; i=0; i--) sa[--wsf[wv[i]]]=y[i];
t=x;
x=y;
y=t;
x[sa[0]]=0;
for(p=1,i=1; i<=n; i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
}
}
void getheight(int *r,int n)//n为添加0后的总长
{
int i,j,k=0;
for(i=1; i<=n; i++) Rank[sa[i]]=i;
for(i=0; i 先来个裸题
洛谷P3809
题目意思:
读入一个长度为 n 的由大小写英文字母或数字组成的字符串,请把这个字符串的所有非空后缀按字典序从小到大排序,然后按顺序输出后缀的第一个字符在原串中的位置。位置编号为 1 到 n 。
就是求sa数组
AC代码
#include
#include
#include
#include
#include
#include
#include
#define pb push_back
#define pback pop_back
#define ll long long
using namespace std;
void read(int &x)
{
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
inline void write(int x)
{
if(x<0) putchar('-'),x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
const int maxn = 1e6+5;//开总串长度,不要忘记连接符
int wa[maxn],wb[maxn],wsf[maxn],wv[maxn],sa[maxn];
int Rank[maxn],height[maxn],s[maxn];
char str1[maxn],str2[maxn];
int cmp(int *r,int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
}
int len ;
void getsa(int *r,int *sa,int n,int m)//n为添加0后的总长
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0; i=0; i--) sa[--wsf[x[i]]]=i;
p=1;
j=1;
for(; p<=n; j*=2,m=p) //倍增的算法
{
for(p=0,i=n+1-j; i<=n; i++) y[p++]=i;
for(i=0; i<=n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0; i<=n; i++) wv[i]=x[y[i]];
for(i=0; i=0; i--) sa[--wsf[wv[i]]]=y[i];
t=x;
x=y;
y=t;
x[sa[0]]=0;
for(p=1,i=1; i<=n; i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
}
}
void getheight(int *r,int n)//n为添加0后的总长
{
int i,j,k=0;
for(i=1; i<=n; i++) Rank[sa[i]]=i;
for(i=0; i rb) swap(ra, rb);
int k = 0;
while((1 << (k + 1)) <= rb-ra) k++;
return min(dp[ra+1][k], dp[rb - (1 << k) + 1][k]);
}
int main(){
scanf("%s",str1);
int pp = 0;
len = strlen (str1);
for(int i = 0; i 后缀数组第一题:
求字符串的子串并且长度不小于m
牛客 CSL的密码
题意:大概就是给你一个长度为n的字符串!求这个字符串的子串的个数!满足一个条件!就是子串的长度至少为m!
我的理解:
不难发现某个子串也就是某个后缀的前缀!!!
那么原来的问题就是转换成求后缀之间的不同前缀的个数!如果按照suffix(sa[1]),suffix(sa[2]),suffix(sa[3]),……,suffix(sa[n])的顺序计算!!!我们会发现每一次新加入的suffix【sa【k】】,都会产生n-sa【i】个前缀!!!(有些人板子这里写法是n-sa【i】+1) 但是其中有height[k]个是和前面的字符串的前缀是相同的。所以suffix(sa[k])将“贡献”出n-sa[k]+1-height[k]个不同的子串。
这个题目求的是长度至少为m!!!所以每次的加入的suffix(sa[k])需要减去少于m个方案数
累加后便是原问题的答案。这个做法的时间复杂度为O(n)。**
AC 代码
#include
#include
#include
#include
#include
#include
#include
#include
typedef long long int ll;
using namespace std;
const int maxn = 2e5+5;//开总串长度,不要忘记连接符
int wa[maxn],wb[maxn],wsf[maxn],wv[maxn],sa[maxn];
int Rank[maxn],height[maxn],s[maxn];
char str1[maxn],str2[maxn];
int cmp(int *r,int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
}
void getsa(int *r,int *sa,int n,int m)
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0; i=0; i--) sa[--wsf[x[i]]]=i;
p=1;
j=1;
for(; p<=n; j*=2,m=p) //倍增的算法
{
for(p=0,i=n+1-j; i<=n; i++) y[p++]=i;
for(i=0; i<=n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0; i<=n; i++) wv[i]=x[y[i]];
for(i=0; i=0; i--) sa[--wsf[wv[i]]]=y[i];
t=x;
x=y;
y=t;
x[sa[0]]=0;
for(p=1,i=1; i<=n; i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
}
}
void getheight(int *r,int n)//n为添加0后的总长
{
int i,j,k=0;
for(i=1; i<=n; i++) Rank[sa[i]]=i;
for(i=0; i>n>>m){
cin>>a;
int pp=0;
for(int i = 0 ;i < n ;i++){
s[pp++]=a[i]-'a'+1;
}
s[pp]=0;
getsa(s,sa,pp,51);
getheight(s,pp);
//int len=a.size();
ll ans=0;
for(int i = 1 ; i<= pp ;i++){
//ans+=n-sa[i]+1-height[i];
ans+=max(0,n-sa[i]-max(m-1,height[i]));
}
cout< 后缀数组第二题:
求不可重叠的重复子串的种类数
Hdu 3518
题意:告诉你一个字符串!让你去求它的子串出现的至少2次以上!并且不能重叠的!!!这样子的子串有多少个
我的理解:题目求的是子串的种类数!!!我们就去枚举 i 属于(1-len/2),很明显长度为i的子串有多少个!!!最后每个长度为i的子串相加就是答案!!!然后就是height【k】>= i 我们就去实时更新这个sa【k】和sa【k-1】,如果最后这个题目相差的值大于 i 说明就是满足题目解
AC 代码
#include
#include
#include
#include
#include
#include
#include
#include
#include
typedef long long int ll;
using namespace std;
const int maxn = 2e4+5;
int wa[maxn],wb[maxn],wsf[maxn],wv[maxn],sa[maxn];
int Rank[maxn],height[maxn],s[maxn];
char str1[maxn],str2[maxn];
int cmp(int *r,int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
}
void getsa(int *r,int *sa,int n,int m)
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0; i=0; i--) sa[--wsf[x[i]]]=i;
p=1;
j=1;
for(; p<=n; j*=2,m=p)
{
for(p=0,i=n+1-j; i<=n; i++) y[p++]=i;
for(i=0; i<=n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0; i<=n; i++) wv[i]=x[y[i]];
for(i=0; i=0; i--) sa[--wsf[wv[i]]]=y[i];
t=x;
x=y;
y=t;
x[sa[0]]=0;
for(p=1,i=1; i<=n; i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
}
}
void getheight(int *r,int n)
{
int i,j,k=0;
for(i=1; i<=n; i++) Rank[sa[i]]=i;
for(i=0; i9) WR(x/10);
putchar(x%10+'0');
}
//求不可重叠的重复子串的种类数
int main(){
while(~scanf("%s",str1)){
getchar();
if(str1[0]=='#')
break;
int pp=0;
for(int i = 0 ; i < strlen(str1) ; i++ ){
s[pp++] = str1[i] - 'a' + 1 ;
}
s[pp]=0;
getsa(s,sa,pp,128);
getheight(s,pp);
ll ans=0;
int minn=1010,maxx=-1;
int flag=0;
for(int i = 1 ; i <= strlen(str1)/2 ; i++ ){
//求不可重叠的话!!!长度最长就是len/2
minn=1010,maxx=-1;
for(int j = 1; j<=pp; j++){
if( height[j] >= i ){
//每次去更新sa【j】的左右端点值
if(sa[j-1]>sa[j]){
maxx=max(maxx,sa[j-1]);
minn=min(minn,sa[j]);
}else{
maxx=max(maxx,sa[j]); // 一开始wa错在sa数组写成s
minn=min(minn,sa[j-1]);
}
}else{
//长度小于i 需要重新去判断
if(minn+i<=maxx){
ans++;
}
minn=1010,maxx=-1;
}
}
//每一个长度去判读下 是不是满足情况
if(minn+i<=maxx){
ans++;
}
}
WR(ans);
puts("");
}
return 0;
}
后缀数组第三题:
求不可重叠的“相似”子串的最长长度
Poj 1743
题意:给你一个字符串!让你去求这个不可重叠的最长的相似子串的长度!!!最后输出这个长度!!!
**相似子串:就是他们之间变化是相同的!!!或者相差的值相同!!!举个例子
- 1 3 5 7 9 11 13 17 19 21 23 最长的长度是5
- 因为这个1 3 5 7 9 和 13 17 19 21 23 它们符合题目意思且不重叠!!!也就是这个相似的子串!!!
我的理解:一开始需要对原来的数字进行一个优化!!!就是我们做它们之间的差值!只要它们的差值也是相同!!!那么也是符合题目意思!!!很显然转换成了求然后利用后缀数组height的性质求子串最长公共前缀即可!!!不可重叠!!!然后的话!!!一开始我没有二分这个长度!!!TlE超时!!!然后这个二分这个长度花了太多的时间去写!!!还是弱啊!!!看样子二分真的很重要
AC 代码
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define INF (1<<30)
typedef long long int ll;
using namespace std;
const int maxn = 2e4+5;
int wa[maxn],wb[maxn],wsf[maxn],wv[maxn],sa[maxn];
int Rank[maxn],height[maxn],s[maxn];
char str1[maxn],str2[maxn];
int cc[maxn];
int cmp(int *r,int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
}
void getsa(int *r,int *sa,int n,int m)
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0; i=0; i--) sa[--wsf[x[i]]]=i;
p=1;
j=1;
for(; p<=n; j*=2,m=p)
{
for(p=0,i=n+1-j; i<=n; i++) y[p++]=i;
for(i=0; i<=n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0; i<=n; i++) wv[i]=x[y[i]];
for(i=0; i=0; i--) sa[--wsf[wv[i]]]=y[i];
t=x;
x=y;
y=t;
x[sa[0]]=0;
for(p=1,i=1; i<=n; i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
}
}
void getheight(int *r,int n)
{
int i,j,k=0;
for(i=1; i<=n; i++) Rank[sa[i]]=i;
for(i=0; i= k){
maxsa = max(maxsa, sa[i]);
minsa = min(minsa, sa[i]);
}
else{
if (maxsa - minsa >= k){
return true;
}
maxsa = sa[i], minsa = sa[i];
}
}
if (maxsa - minsa >= k){
return true;
}
return false;
}
int main(){
int n;
while(scanf("%d",&n) && n ){
pp = 0;
for(int i = 0 ; i < n ;i++){
scanf("%d",&cc[i]);
}
for(int i = 1 ; i < n ; i++){
s[pp++]=cc[i]-cc[i-1]+100; //保证是正数
}
s[pp] = 0 ;
getsa(s,sa,pp,200); //这里一定要开大点!!!不然就是RE
getheight(s,pp);
int l = 0, r = pp, mid;
//下面这个二分写了好久!!!
while(l<=r){
mid=(l+r)/2;
if(check(mid)){ //这个check(len) 判断长度为len的是不是满足情况
l=mid+1;
}else{
r=mid-1;
}
}
if(r>=4) printf("%d",r+1);
else printf("0");
puts("");
}
return 0;
}
后缀数组第四题:
求可重叠的出现k次子串的最长长度
Poj 3261
题意:找出出现k次的可重叠的最长子串的长度
我的理解:二分长度!!!对于每个长度而言的话!!!扫描一遍这个height【i】数组,最后要是出现了k次的话,check()函数判断为真
AC 代码
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define INF (1<<30)
typedef long long int ll;
using namespace std;
const int maxn = 2e4+5;
int wa[maxn],wb[maxn],wsf[maxn],wv[maxn],sa[maxn];
int Rank[maxn],height[maxn],s[maxn];
char str1[maxn],str2[maxn];
int cc[maxn];
int cmp(int *r,int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
}
void getsa(int *r,int *sa,int n,int m)
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0; i=0; i--) sa[--wsf[x[i]]]=i;
p=1;
j=1;
for(; p<=n; j*=2,m=p)
{
for(p=0,i=n+1-j; i<=n; i++) y[p++]=i;
for(i=0; i<=n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0; i<=n; i++) wv[i]=x[y[i]];
for(i=0; i=0; i--) sa[--wsf[wv[i]]]=y[i];
t=x;
x=y;
y=t;
x[sa[0]]=0;
for(p=1,i=1; i<=n; i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
}
}
void getheight(int *r,int n)
{
int i,j,k=0;
for(i=1; i<=n; i++) Rank[sa[i]]=i;
for(i=0; i= len ){
cnt++;
if(cnt>=k){
return 1;
}
}else{
cnt = 1;
}
if(cnt>=k)
return 1;
}
return 0;
}
int main(){
int maxlen=0;
while(~scanf("%d %d",&n,&k)){
for(int i = 0; i < n; i++){
cin>>s[i];
s[i]++;
maxlen=max(maxlen,s[i]); //比较一个小的细节
}
s[n]=0;
getsa(s,sa,n,maxlen+2);
getheight(s,n);
int l = 1,r = n,mid,ans=0;
while(l<=r){
mid=(l+r)/2;
if(check(mid)){
ans=mid;
l=mid+1;
}else{
r=mid-1;
}
}
cout< 后缀数组第五题:
求两个串的最长公共子串
Poj 2774
题意:给你两个串!!!求最长的公共子串的长度!!!
我的理解:中间去用一个没有出现的字符去连接两个串!最后的话跑一遍这个height数组就是!!!但是要注意的就是每次更新这个ans的时候!判断下这个sa【k】与sa【k-1】是不是在连个串就行!!!
AC 代码
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define maxn 200005
typedef long long int ll;
using namespace std;
int wa[maxn],wb[maxn],wsf[maxn],wv[maxn],sa[maxn];
int Rank[maxn],height[maxn],s[maxn];
char str1[maxn],str2[maxn];
int cmp(int *r,int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
}
void getsa(int *r,int *sa,int n,int m)
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0; i=0; i--) sa[--wsf[x[i]]]=i;
p=1;
j=1;
for(; p<=n; j*=2,m=p)
{
for(p=0,i=n+1-j; i<=n; i++) y[p++]=i;
for(i=0; i<=n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0; i<=n; i++) wv[i]=x[y[i]];
for(i=0; i=0; i--) sa[--wsf[wv[i]]]=y[i];
t=x;
x=y;
y=t;
x[sa[0]]=0;
for(p=1,i=1; i<=n; i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
}
}
void getheight(int *r,int n)
{
int i,j,k=0;
for(i=1; i<=n; i++) Rank[sa[i]]=i;
for(i=0; ians){
if( sa[i-1] < len&&sa[i]>len)
ans=height[i];
if(sa[i-1]>len&&sa[i] 后缀数组第六题:
求多个串的公共最长串
Poj 1226
题意:给定n个字符串,求出现或反转后出现在每个字符串中的最长子串的长度
举个例子
- 2
- ABCD
- DCBA
- 最长的长度是4
- 题目的意思就是可以去翻转(ABCD 跟DCBA效果一样)
我的理解:求公共的子串!转换成这个后缀的前缀!然后这个height数组发挥它的作用!思路就将每个串连接起来,中间用一个没有出现的字符!最后再将字符翻转起来!也连起来!!!这个题目唯一需要注意的就是这个pos数组!!!我需要去记入这个pos【sa【k】】的值!!!最后判断这个值是不是都在n个子串出现过!!!
体会:Runtime Error 20发!!!后面看了下评论区!才知道这个字符可能是数字!!!太菜了!!!
AC 代码
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define maxn 20005
typedef long long int ll;
using namespace std;
int wa[maxn],wb[maxn],wsf[maxn],wv[maxn],sa[maxn];
int Rank[maxn],height[maxn],s[maxn];
int cmp(int *r,int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
}
void getsa(int *r,int *sa,int n,int m)
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0; i=0; i--) sa[--wsf[x[i]]]=i;
p=1;
j=1;
for(; p<=n; j*=2,m=p)
{
for(p=0,i=n+1-j; i<=n; i++) y[p++]=i;
for(i=0; i<=n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0; i<=n; i++) wv[i]=x[y[i]];
for(i=0; i=0; i--) sa[--wsf[wv[i]]]=y[i];
t=x;
x=y;
y=t;
x[sa[0]]=0;
for(p=1,i=1; i<=n; i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
}
}
void getheight(int *r,int n)
{
int i,j,k=0;
for(i=1; i<=n; i++) Rank[sa[i]]=i;
for(i=0; i=mid)
{
for(j = 0; j=k) return true; //判断的就是每个位置是不是出现
cnt = 0;
memset(vis,0,sizeof(vis));
}
}
if(cnt>=k) return true;
return false;
}
int main(){
int t;
int len;
scanf("%d",&t);
while(t--){
scanf("%d",&n);
int pp = 0;
int mark = 250;
for(int i = 0 ; i < n; i++){
scanf("%s",str1);
len = strlen(str1);
for(int j = 0; j < len; j++){
pos[pp] = i; //记入的是出现在第i个串的位置
s[pp++] = str1[j] -'0'+1; //这里一定是减去‘0’ 因为数据里面有数字
}
s[pp++] = mark++;
for(int j = len-1 ; j >= 0;j--){
pos[pp] = i;
s[pp++] = str1[j] - '0' +1;
}
s[pp++] = mark++;
}
//这里的话需要pp-- 因为每个人的板子不一样!!!然后的话看每个人理解吧
pp--;
s[pp] = 0;
getsa(s,sa,pp,500);
getheight(s,pp);
int l = 0 ,r = 100, mid, ans = 0 ;
while( l <= r ){
mid = (l+r)/2;
if(check(mid,pp,n)){
ans = mid;
l = mid+1;
}else{
r = mid - 1;
}
}
printf("%d\n",ans);
}
return 0;
}
后缀数组第七题:
求一个串的不同子串
SPOJ - SUBST1
题意:就是求一个串的子串
我的理解:文章一开始已经写了这个子串的思路!!!但是为什么还要去写呢!!!其实就是自己写这题的一点感受!为什么会Wrong answer!代码会补充!!! 补充一个求子串的思路:假设这个串中所以字符不相等!!!那么对ans的贡献就是len(len+1)/2,然后扫一遍这个height数组减去公共的前缀值!!那么也是答案!!!*
AC 代码
#include
#include
#include
#include
#include
#include
#define pb push_back
#define pback pop_back
#define ll long long
using namespace std;
const int maxn = 5e4+5;//开总串长度,不要忘记连接符
int wa[maxn],wb[maxn],wsf[maxn],wv[maxn],sa[maxn];
int Rank[maxn],height[maxn],s[maxn];
char str1[maxn],str2[maxn];
int cmp(int *r,int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
}
void getsa(int *r,int *sa,int n,int m)//n为添加0后的总长
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0; i=0; i--) sa[--wsf[x[i]]]=i;
p=1;
j=1;
for(; p<=n; j*=2,m=p) //倍增的算法
{
for(p=0,i=n+1-j; i<=n; i++) y[p++]=i;
for(i=0; i<=n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0; i<=n; i++) wv[i]=x[y[i]];
for(i=0; i=0; i--) sa[--wsf[wv[i]]]=y[i];
t=x;
x=y;
y=t;
x[sa[0]]=0;
for(p=1,i=1; i<=n; i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
}
}
void getheight(int *r,int n)//n为添加0后的总长
{
int i,j,k=0;
for(i=1; i<=n; i++) Rank[sa[i]]=i;
for(i=0; i'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
int main(){
int t;
scanf("%d",&t);
while(t--){
int pp = 0;
scanf("%s",str1);
int len = strlen(str1);
for(int i = 0 ; i < len; i++){
s[pp++] = str1[i] - '0' +100; //一开始另外一个错在这里!!!以为只能是字母!!!没有想到还有可以是数字0 !! 所以直接加100
}
s[pp] = 0;
int ans = 1ll*len*(len+1)/2; //这里可以爆ll
getsa(s,sa,pp,2510);
getheight(s,pp);
//cout< 后缀数组第八题:
求重复次数最多的连续重复子串
SPOJ 687. Repeats
题意:给你一个串让你求出重复次数最多的连续重复子串的重复次数
我的理解:
哎!!!实在是看题解!!!发现还有人写这个论文!!!
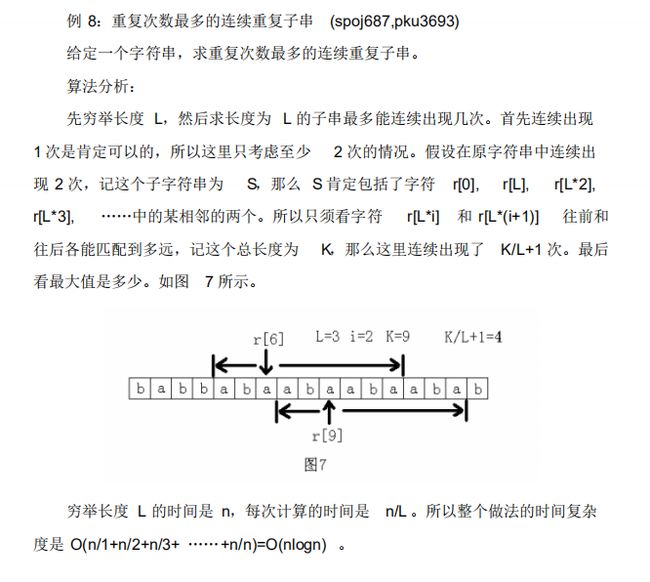
大概的思路就是:
首先去预处理下这个RMQ() 求区间【a,b】的公共前缀和的最小值
接下来每次枚举循环的长度len!每次的话我们去算这个区间【i,i+len】的最长公共前缀!然后的话lcp(最长公共前缀) / 循环节长度 +1 就是答案!!!但是有个情况你需要去考虑!要是lcp%循环节长度!=0很有可能多出来的字符部分 跟这个前面的字符也可以构成循环节!!!
接下来就是需要去算后面多出来的字符是不是跟前面能构成!
AC 代码
#include
#include
#include
#include
#include
#include
#define pb push_back
#define pback pop_back
#define ll long long
using namespace std;
const int maxn = 5e4+5;//开总串长度,不要忘记连接符
int wa[maxn],wb[maxn],wsf[maxn],wv[maxn],sa[maxn];
int Rank[maxn],height[maxn],s[maxn];
char str1[maxn],str2[maxn];
int cmp(int *r,int a,int b,int k)
{
return r[a]==r[b]&&r[a+k]==r[b+k];
}
void getsa(int *r,int *sa,int n,int m)//n为添加0后的总长
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0; i=0; i--) sa[--wsf[x[i]]]=i;
p=1;
j=1;
for(; p<=n; j*=2,m=p) //倍增的算法
{
for(p=0,i=n+1-j; i<=n; i++) y[p++]=i;
for(i=0; i<=n; i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0; i<=n; i++) wv[i]=x[y[i]];
for(i=0; i=0; i--) sa[--wsf[wv[i]]]=y[i];
t=x;
x=y;
y=t;
x[sa[0]]=0;
for(p=1,i=1; i<=n; i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)? p-1:p++;
}
}
void getheight(int *r,int n)//n为添加0后的总长
{
int i,j,k=0;
for(i=1; i<=n; i++) Rank[sa[i]]=i;
for(i=0; i rb) swap(ra, rb);
int k = 0;
while((1 << (k + 1)) <= rb-ra) k++;
return min(dp[ra+1][k], dp[rb - (1 << k) + 1][k]);
}
void read(int &x)
{
int f=1;x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
x*=f;
}
int main(){
int t;
int n;
char xx;
scanf("%d",&t);
while(t--){
int pp = 0;
scanf("%d", &n);
for(int i = 0; i < n; i++){
getchar();
scanf("%c",&xx);
s[pp++] = xx -'0' +100;
}
s[pp] = 0;
getsa(s,sa,pp,251);
getheight(s,pp);
RMQ(pp);
int cnt = 0;
for(int len = 1; len <= pp ; len++){
for(int i = 0; i + len < pp; i+=len){
int lcp = askRMQ(i, i+len);
int times = lcp / len +1;
int k = i - (len - lcp % len);
if(k >= 0 && lcp % len){
if(askRMQ(k, k + len) >= lcp)
times++;
}
cnt = max(cnt, times);
}
}
printf("%d\n",cnt);
}
return 0;
}
后缀数组第九题:
求两个串的最长公共子串
LA-4513
题意:求一个串的至少重复m次可以重叠的子串的最长长度
我的理解:二分(长度)+ 扫描height
AC 代码
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include