数据结构与算法(Python版) | (8) 递归(上)
本专栏主要基于北大的数据结构与算法教程(Python版)进行整理，包括课程笔记和OJ作业。
课程链接
1. 什么是递归
定义
- 递归是一种解决问题的方法，其精髓在于：
1）将问题分解为规模更小的相同问题，
2） 持续分解，直到问题规模小到可以用非常简单直接的方式来解决。
3） 递归的问题分解方式非常独特，其算法方面的明显特征就是:在算法流程中调用自身。 - 递归为我们提供了一种对复杂问题的优雅解决方案，精妙的递归算法常会出奇简单 ，令人赞叹。
初识递归:数列求和
- 问题:给定一个列表，返回所有数的和：
列表中数的个数不定，需要一个循环和一个累加 变量来迭代求和。 - 程序很简单，但假如没有循环语句?
既不能用for，也不能用while。 还能对不确定长度的列表求和么?
def listsum(numList):
theSum = 0
for i in numList:
theSum = theSum + i
return theSum
- 我们认识到求和实际上最终是由一次次的加法实现的，而加法恰有2个操作数，这个是确定的。
- 看看怎么想办法，将问题规模较大的列表求和，分解为规模较小而且固定的2个数求和(加法)?
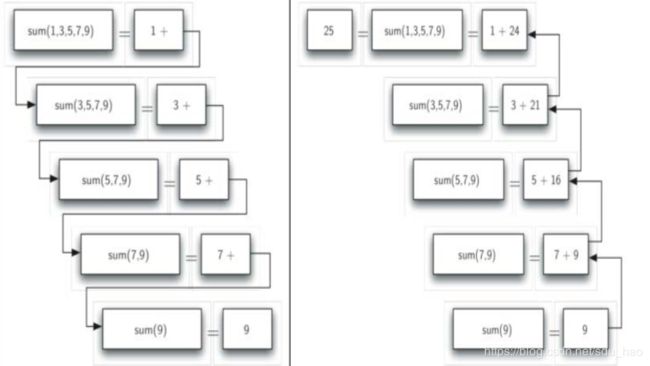
同样是求和问题，但规模发生了变化，符合递归解决问题的特征! - 换个方式来表达数列求和:全括号表达式 (1+(3+(5+(7+9))))
- 上面这个式子，最内层的括号(7+9)，这 是无需循环即可计算的，实际上整个求和 的过程是这样(每次只计算两个数的和):
- 观察上述过程中所包含的重复模式，可以把求和问题归纳成这样:
数列的和=“首个数”+“余下数列”的和 - 如果数列包含的数少到只有1个的话，它的和就是这个数了
这是规模小到可以做最简单的处理
- 上面的递归算法变成程序
def listsum(numList):
if len(numList) == 1: #最小规模
return numList[0]
else:
return numList[0] + listSum(numList[1:]) #分解问题 减小规模（列表切片）； 调用自身。
- 要点
1）问题分解为更小规模的相同问题，并表现为 “调用自身”
2）对“最小规模”问题的解决:简单直接
递归程序如何被执行?
- 递归函数调用和返回过程的链条
递归“三定律”
-
为了向阿西莫夫的“机器人三定律”致敬 ，递归算法也总结出“三定律”
1）递归算法必须有一个基本结束条件(最小规 模问题的直接解决)
2）递归算法必须能改变状态向基本结束条件演 进(减小问题规模)
3）递归算法必须调用自身(解决减小了规模的相同问题) -
数列求和问题首先具备了基本结束条件: 当列表长度为1的时候，直接输出所包含的唯一数
-
数列求和处理的数据对象是一个列表，而基本结束条件是长度为1的列表，那递归算法就要改变列表并向长度为1的状态演进。
我们看到其具体做法是将列表长度减少1。 -
调用自身是递归算法中最难理解的部分，实际上我们理解为“问题分解成了规模更小的相同问题”就可以了。
在数列求和算法中就是“更短数列的求和问题”
2. 递归的应用:任意进制转换
整数转换为任意进制
-
这个在数据结构栈里讨论过的算法，又回来了!
递归和栈，一定有关联 -
如果上次你被“入栈”“出栈”搞得挺晕乎的话，这次递归算法一定会让你感到清新
而且这次我们要解决从二进制到十六进制的任意进制转换 -
我们用最熟悉的十进制分析下这个问题
1）十进制有十个不同符号:convString = “0123456789”
2）比十小的整数，转换成十进制，直接查表就可以 了:convString[n]
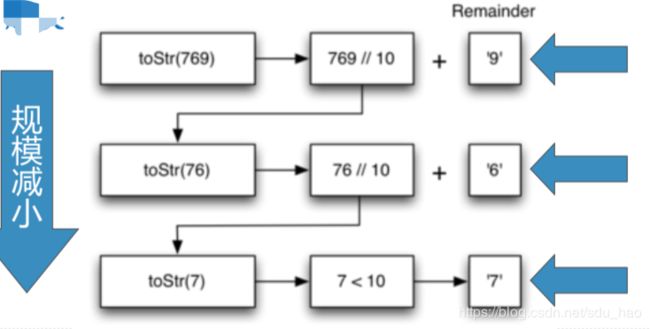
3） 想办法把比十大的整数，拆成一系列比十小的整数，逐个查表：比如七百六十九，拆成七、六、九，查表得到 769就可以了。 -
所以，在递归三定律里，我们找到了“基 本结束条件”，就是小于十的整数
拆解整数的过程就是向“基本结束条件”演进的 过程 -
我们用整数除，和求余数两个计算来将整数一步步拆开：
1）除以“进制基base”(// base)
2）对“进制基”求余数(% base) -
问题就分解为:
1）余数总小于“进制基base”，是“基本结束条件 ”，可直接进行查表转换
2）整数商成为“更小规模”的相同问题，通过递归调用自身解决。
-
代码
def toStr(n,base):
convertString = "0123456789ABCDEF"
if n<base:
return covertString[n] #最小规模
else:
return toStr(n//base,base) + covertString[n%base] #减小规模，调用自身
3. 递归调用的实现
递归调用实现
- 当一个函数被调用的时候，系统会把调用时的现场数据压入到系统调用栈；每次调用，压入栈的现场数据称为栈帧；当函数返回时，要从调用栈的栈顶取得返回地址
，恢复现场，弹出栈帧，按地址返回（后进先出）。
Python中的递归深度限制
- 在调试递归算法程序的时候经常会碰到这样的错误:RecursionError
递归的层数太多，系统调用栈容量有限
- 这时候要检查程序中是否忘记设置基本结 束条件，导致无限递归
或者向基本结束条件演进太慢，导致递归层数太多，调用栈溢出。
def tell_story():
print("从前有座山，山里有座庙，庙里有个老和尚，他在讲：")
tell_story()
print("给你讲个故事")
tell_story()
- 在Python内置的sys模块可以获取和调整最大递归深度
递归的故事
4. 递归可视化:分形树
递归可视化:图示
- 前面的种种递归算法展现了其简单而强大 的一面，但还是难有个直观的概念
- 下面我们通过递归作图来展现递归调用的 视觉影像
- Python的海龟作图系统turtle module
1）Python内置，随时可用，以LOGO语言的创意为 基础
2）其意象为模拟海龟在沙滩上爬行而留下的足迹：
爬行:forward(n); backward(n)
转向:left(a); right(a)
抬笔放笔:penup(); pendown()
笔属性:pensize(s); pencolor© - 示例代码
import turtle
t = turtle.Turtle()
#开始做图
t.forward(100) #前行100 （默认向右）
turtle.done() #作图结束
import turtle
t = turtle.Turtle()
for i in range(4):
t.forward(100) #当前方向前进100
t.right(90) #右转90度
turtle.done()
import turtle
t = turtle.Turtle()
t.pencolor('red')
t.pensize(3)
for i in range(5):
t.forward(100) #当前方向前进100
t.right(144) #右转144度
t.hideturtle()
turtle.done()
一个递归作图的例子:螺旋
import turtle
t = turtle.Turtle()
def drawSpiral(t,linelen):
if linelen > 0: #最小规模，0直接退出
t.forward(linelen)
t.right(90)
drawSpiral(t,linelen-5) #减小规模 长度-5 调用自身
drawSpiral(t,100)
turtle.done()
分形树:自相似递归图形
- 分形Fractal，是1975年由Mandelbrot 开创的新学科
“一个粗糙或零碎的几何形状，可以分成数个部 分，且每一部分都(至少近似地)是整体缩小后 的形状”，即具有自相似的性质。
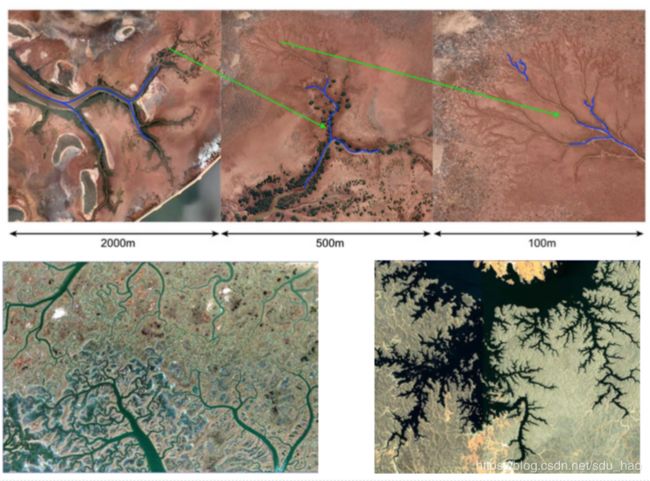
- 自然界中能找到众多具有分形性质的物体
海岸线、山脉、闪电、云朵、雪花、树
http://paulbourke.net/fractals/googleearth/
http://recursivedrawing.com/
自然界不是平滑的
分形树:自相似递归图形
- 自然现象中所具备的分形特性，使得计算机可以通过分形算法生成非常逼真的自然场景(如游戏中的场景)
- 分形是在不同尺度上都具有相似性的事物
我们能看出一棵树的每个分叉和每条树枝，实际 上都具有整棵树的外形特征(也是逐步分叉的) - 这样，我们可以把树分解为三个部分:树 干、左边的小树、右边的小树（左右小树，又可以分为树干，左边的小小树，右边的小小树…）
分解后，正好符合递归的定义:对自身的调用
- 代码
import turtle
def tree(branch_len):
if branch_len > 5: #树干长度<=5就不再继续画了 即递归结束条件
t.forward(branch_len) #画树干
t.right(20) #右倾斜20度
tree(branch_len - 15) #画右边的小树 树干长度-15
t.left(40) #向左回40度 即左倾斜20度
tree(branch_len - 15) #画左边的小树 树干长度-15
t.right(20) #右回20度 回正
t.backward(branch_len) #退回原位置
t = turtle.Turtle()
t.left(90)
t.penup()
t.backward(100)
t.pendown()
t.pencolor('green')
t.pensize(2)
tree(75) #画树干长度75的二叉树
t.hideturtle()
turtle.done()
5. 递归可视化:谢尔宾斯基三角形
谢尔宾斯基Sierpinski三角形
- 分形构造，平面称谢尔宾斯基三角形，立体称谢尔宾斯基金字塔
实际上，真正的谢尔宾斯基三角形是完全不可见 的，其面积为0，但周长无穷，是介于一维和二 维之间的分数维(约1.585维)构造。(谢尔宾斯基金字塔体积为0，表面积无穷)
谢尔宾斯基三角形:作图思路
-
根据自相似特性，谢尔宾斯基三角形是由 3个尺寸减半的谢尔宾斯基三角形按照品字形拼叠而成。
由于我们无法真正做出谢尔宾斯基三角形( degree->∞，看不到了)，只能做degree有限的近似图形。
-
在degree有限的情况下，degree=n的三角形，是由3个degree=n-1的三角形按照品字形拼叠而成。
同时，这3个degree=n-1的三角形边长均为 degree=n的三角形的一半(规模减小)。
当degree=0，则就是一个等边三角形，这是递 归基本结束条件 -
代码
import turtle
def sierpinski(degree,points):
colormap = ['blue','red','green','white','yellow','orange']
drawTriangle(points,colormap[degree]) #绘制等边三角形 points字典 存储三个顶点坐标
if degree > 0: #最小规模 0 直接退出；结束条件
#减小规模 getMid边长减半（原来的两个顶点取中点）
#调用自身 左、上、右次序
sierpinski(degree-1,{'left':points['left'],'top':getMid(points['left'],points['top']),'right':getMid(points['left'],points['right'])})
sierpinski(degree-1,{'left':getMid(points['left'],points['top']),'top':points['top'],'right':getMid(points['top'],points['right'])})
sierpinski(degree-1,{'left':getMid(points['left'],points['right']),'top':getMid(points['top'],points['right']),'right':points['right']})
def drawTriangle(points,color): #绘制等边三角形
t.fillcolor(color)
t.up()
t.goto(points['top'])
t.down()
t.begin_fill()
t.goto(points['left'])
t.goto(points['right'])
t.goto(points['top'])
t.end_fill()
def getMid(p1,p2): #取两个点中点
return ( (p1[0]+p2[0]) / 2, (p1[1] + p2[1]) / 2)
t = turtle.Turtle()
points = {'left':(-200,-100),'top':(0,200),'right':(200,-100)} #外轮廓三个顶点
sierpinski(5,points) #画degree=5的三角形
turtle.done()
6. 递归的应用:汉诺塔
复杂递归问题:汉诺塔
- 汉诺塔问题是法国数学家Edouard Lucas于 1883年，根据传说提出来的。
- 传说在一个印度教寺庙里，有3根柱子，其中 一根套着64个由小到大的黄金盘片，僧侣们 的任务就是要把这一叠黄金盘从一根柱子搬 到另一根，但有两个规则:
1）一次只能搬1个盘子
2）大盘子不能叠在小盘子上 - 神的旨意说一旦这些盘子完成迁移：寺庙将会坍塌，世界将会毁灭…神的旨意是千真万确的!
汉诺塔问题
- 虽然这些黄金盘片跟世界末日有着神秘的联系，但我们却不必太担心，据计算，要搬完这64个盘片（宇宙至今的寿命才170亿年）:
- 我们还是从递归三定律来分析汉诺塔问题
基本结束条件(最小规模问题)，如何减小规模，调用自身
汉诺塔问题:分解为递归形式
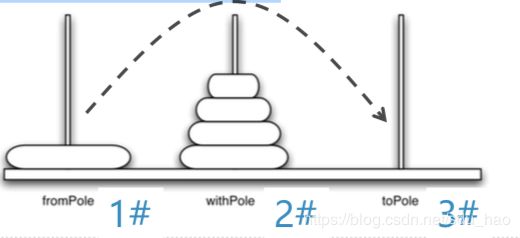
- 假设我们有5个盘子，穿在1#柱，需要挪 到3#柱
1）如果能有办法把最上面的一摞4个盘子统统挪到 2#柱，那问题就好解决了:
2）把剩下的最大号盘子直接从1#柱挪到3#柱
3）再用同样的办法把2#柱上的那一摞4个盘子挪到3#柱，就完成了整个移动
汉诺塔问题:分析
- 接下来问题就是解决4个盘子如何能从1# 挪到2#?
1）此时问题规模已经减小!
2）同样是想办法把上面的一摞3个盘子挪到3#柱，
3）把剩下最大号盘子从1#挪到2#柱，
4）再用同样的办 法把一摞3个盘子从3#挪到2#柱 - 一摞3个盘子的挪动也照此:分为上面一摞2个，和下面最大号盘子
- 那么2个盘子怎么移动?
- 不行，就再分解为1个盘子的移动（直接移动即可）
汉诺塔问题:递归思路
-
将盘片塔从开始柱，经由中间柱，移动到 目标柱:
1）首先将上层N-1个盘片的盘片塔，从开始柱，经由目标柱，移动到中间柱;
2）然后将第N个(最大的)盘片，从开始柱，（直接）移动到目标柱;
3）最后将放置在中间柱的N-1个盘片的盘片塔，经 由开始柱，移动到目标柱。 -
基本结束条件，也就是最小规模问题是:1个盘片的移动问题
-
代码（ 上面的思路用Python写出来，几乎跟语 言描述一样）
def moveTower(height,fromPole,withPole,toPole):
if height >=1:
moveTower(height-1,fromPole,toPole,withPole)
moveDisk(height,fromPole,toPole)
moveTower(height-1,withPole,fromPole,toPole)
def moveDisk(disk,fromPole,toPole):
print(f"Moving Disk[{disk}] from {fromPole} to {toPole}") #格式化字符串
moveTower(3,"#1","#2","#3")
7. 递归的应用:探索迷宫
探索迷宫
- 将海龟放在迷宫中间，如何能找到出口
- 首先，我们将整个迷宫的空间(矩形)分 为行列整齐的方格，区分出墙壁和通道。
给每个方格具有行列位置，并赋予“墙壁”、“ 通道”的属性
迷宫的数据结构
- 考虑用矩阵方式来实现迷宫数据结构
- 采用“数据项为字符列表的列表”这种两级列表 的方式来保存方格内容
- 采用不同字符来分别代表“墙壁+”、“通道(空格)” 、“海龟投放点S”
3）可以在一个文本文件中编辑一个迷宫，然后再从文本文件逐行读入迷宫数据
- Maze Class
class Maze:
def __init__(self,mazeFileName):
rowsInMaze = 0
columnsInMaze = 0
self.mazelist = []
mazeFile = open(mazeFileName,'r')
for line in mazeFile: #遍历每一行
rowList = []
col = 0
for ch in line[:-1]: #遍历每一行字符列表中的每个字符（：-1 除去末尾换行符）
rowList.append(ch)
if ch == 'S':
self.startRow = rowsInMaze
self.startCol = col
col = col + 1
rowsInMaze = rowsInMaze + 1
self.mazelist.append(rowList)
columnsInMaze = len(rowList)
- 读入数据文件成功后
mazelist如下图示意:
探索迷宫:算法思路
- 确定了迷宫数据结构之后，我们知道，对 于海龟来说，其身处某个方格之中
- 它所能移动的方向，必须是向着通道的方向
- 如果某个方向是墙壁方格，就要换一个方向移动
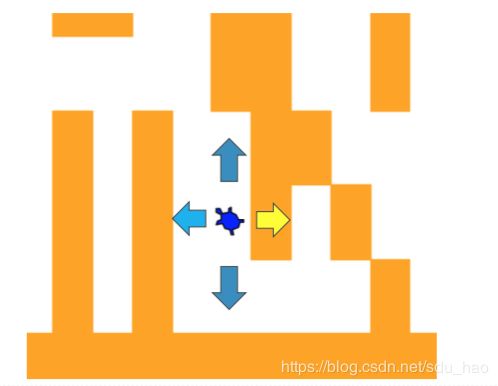
- 这样，探索迷宫的递归算法思路如下:
- 将海龟从原位置向北移动一步，以新位置递归调 用探索迷宫寻找出口;
- 如果上面的步骤找不到出口，那么将海龟从原位置向南移动一步，以新位置递归调用探索迷宫;
- 如果向南还找不到出口，那么将海龟从原位置向西移动一步，以新位置递归调用探索迷宫;
- 如果向西还找不到出口，那么将海龟从原位置向东移动一步，以新位置递归调用探索迷宫;
- 如果上面四个方向都找不到出口，那么这个迷宫 没有出口!
- 思路看起来很完美，但有些细节至关重要
- 如果我们向某个方向(如北)移动了海龟，那么 如果新位置的北正好是一堵墙壁，那么在新位置 上的递归调用就会让海龟向南尝试
- 可是新位置的南边一格，正好就是递归调用之前的原位置，这样就陷入了无限递归的死循环之中
-
所以需要有个机制记录海龟所走过（探索过）的路径
沿途洒“面包屑”，一旦前进方向发现“面包屑 ”，就不能再踩上去，而必须换下一个方向尝试
对于递归调用来说，就是某方向的方格上发现“面包屑”，就立即从递归调用返回上一级。 -
递归调用的“基本结束条件”归纳如下:
1）海龟碰到“墙壁”方格，递归调用结束，返回失 败;
2）海龟碰到“面包屑”方格，表示此方格已访问过，递归调用结束，返回失败;
3）海龟碰到“出口”方格，即“位于边缘的通道”方格，递归调用结束，返回成功!
4） 海龟在四个方向上探索都失败，递归调用结束，返回失败
探索迷宫:辅助的动画过程
- 为了让海龟在迷宫图里跑起来，我们给迷宫数据结构Maze Class添加一些成员和方法
- 探索函数
def searchFrom(maze,startRow,startColumn):
#1. 碰到墙壁 返回失败
maze.updatePosition(startRow,startColumn)
if maze[startRow][startColumn] == OBSTACLE:
return False
#2. 碰到面包屑，或者死胡同，返回失败
if maze[startRow][startColumn] == TRIED or maze[startRow][startColumn] == DEAD_END:
return False
#3. 碰到了出口，返回成功！
if maze.isExit(startRow,startColumn):
maze.updatePosition(startRow,startColumn,PART_OF_PATH)
return True
#4. 洒一下面包屑，继续探索
maze.updatePosition(startRow,startColumn,TRIED)
#向北南西东4个方向依次探索 or具有短路效应（第一个表达式为True其余表达式都不会计算，第一个为False时，才会计算第二个...）
found = searchFrom(maze,startRow-1,startColumn) or searchFrom(maze,startRow+1,startColumn) or searchFrom(maze,startRow,startColumn-1) or searchFrom(maze,startRow,startColumn+1)
#如果探索成功 标记当前点（为可行路径中的一点），失败则标记为死胡同
if found:
maze.updatePosition(startRow,startColumn,PART_OF_PATH)
else:
maze.updatePosition(startRow,startColumn,DEAD_END)
return found
- 完整代码
import turtle
PART_OF_PATH = 'O'
TRIED = '.'
OBSTACLE = '+'
DEAD_END = '-'
class Maze:
def __init__(self,mazeFileName):
rowsInMaze = 0
columnsInMaze = 0
self.mazelist = []
mazeFile = open(mazeFileName,'r')
rowsInMaze = 0
for line in mazeFile:
rowList = []
col = 0
for ch in line[:-1]:
rowList.append(ch)
if ch == 'S':
self.startRow = rowsInMaze
self.startCol = col
col = col + 1
rowsInMaze = rowsInMaze + 1
self.mazelist.append(rowList)
columnsInMaze = len(rowList)
self.rowsInMaze = rowsInMaze
self.columnsInMaze = columnsInMaze
self.xTranslate = -columnsInMaze/2
self.yTranslate = rowsInMaze/2
self.t = turtle.Turtle()
self.t.shape('turtle')
self.wn = turtle.Screen()
self.wn.setworldcoordinates(-(columnsInMaze-1)/2-.5,-(rowsInMaze-1)/2-.5,(columnsInMaze-1)/2+.5,(rowsInMaze-1)/2+.5)
def drawMaze(self):
self.t.speed(10)
for y in range(self.rowsInMaze):
for x in range(self.columnsInMaze):
if self.mazelist[y][x] == OBSTACLE:
self.drawCenteredBox(x+self.xTranslate,-y+self.yTranslate,'orange')
self.t.color('black')
self.t.fillcolor('blue')
def drawCenteredBox(self,x,y,color):
self.t.up()
self.t.goto(x-.5,y-.5)
self.t.color(color)
self.t.fillcolor(color)
self.t.setheading(90)
self.t.down()
self.t.begin_fill()
for i in range(4):
self.t.forward(1)
self.t.right(90)
self.t.end_fill()
def moveTurtle(self,x,y):
self.t.up()
self.t.setheading(self.t.towards(x+self.xTranslate,-y+self.yTranslate))
self.t.goto(x+self.xTranslate,-y+self.yTranslate)
def dropBreadcrumb(self,color):
self.t.dot(10,color)
def updatePosition(self,row,col,val=None):
if val:
self.mazelist[row][col] = val
self.moveTurtle(col,row)
if val == PART_OF_PATH:
color = 'green'
elif val == OBSTACLE:
color = 'red'
elif val == TRIED:
color = 'black'
elif val == DEAD_END:
color = 'red'
else:
color = None
if color:
self.dropBreadcrumb(color)
def isExit(self,row,col):
return (row == 0 or
row == self.rowsInMaze-1 or
col == 0 or
col == self.columnsInMaze-1 )
def __getitem__(self,idx):
return self.mazelist[idx]
def searchFrom(maze, startRow, startColumn):
# try each of four directions from this point until we find a way out.
# base Case return values:
# 1. We have run into an obstacle, return false
maze.updatePosition(startRow, startColumn)
if maze[startRow][startColumn] == OBSTACLE :
return False
# 2. We have found a square that has already been explored
if maze[startRow][startColumn] == TRIED or maze[startRow][startColumn] == DEAD_END:
return False
# 3. We have found an outside edge not occupied by an obstacle
if maze.isExit(startRow,startColumn):
maze.updatePosition(startRow, startColumn, PART_OF_PATH)
return True
maze.updatePosition(startRow, startColumn, TRIED)
# Otherwise, use logical short circuiting to try each direction
# in turn (if needed)
found = searchFrom(maze, startRow-1, startColumn) or \
searchFrom(maze, startRow+1, startColumn) or \
searchFrom(maze, startRow, startColumn-1) or \
searchFrom(maze, startRow, startColumn+1)
if found:
maze.updatePosition(startRow, startColumn, PART_OF_PATH)
else:
maze.updatePosition(startRow, startColumn, DEAD_END)
return found
myMaze = Maze('maze2.txt')
myMaze.drawMaze()
myMaze.updatePosition(myMaze.startRow,myMaze.startCol)
searchFrom(myMaze, myMaze.startRow, myMaze.startCol)
迷宫文件maze2.txt
