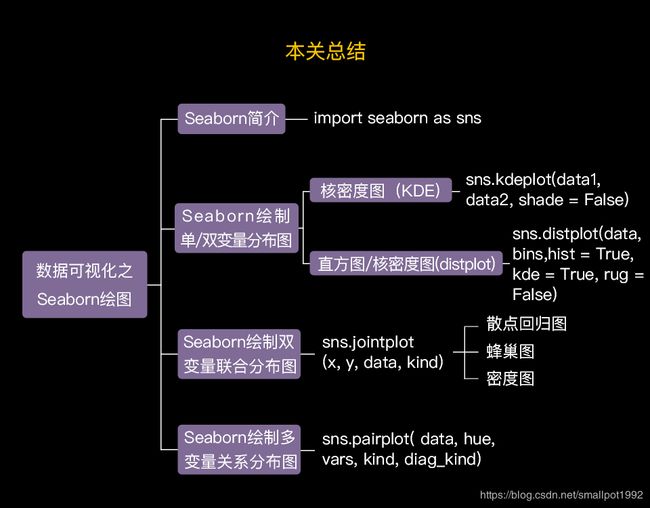
数据可视化之Seaborn绘图

知识结构

Seaborn简介

话不多说，我们首先来欣赏几张 Seaborn 绘制的图形，一睹为快。

是不是很酷炫？学习完Seaborn的相关内容，你也可以轻松地画出这样的图。

Seaborn 是 Python 中基于 matplotlib 的统计绘图模块。如果说 matplotlib 是“tries to make easy things easy and hard things possible”，那么 Seaborn 则是让“hard things”也变简单。

Seaborn 在 matplotlib 的基础上进行了更高级的封装，这样做图会更加方便快捷。我们可以仅仅通过一些极简的代码，就能做出很具有分析价值而且又十分美观的图形。

导入Seaborn我们使用：

import seaborn as sns

通常情况下我们习惯使用 sns 作为 Seaborn 的别名。

成功导入Seaborn之后我们就可以开启绘图之旅了。在今天的学习中，我们主要来为大家介绍连续数值型数据绘图，我们将从连续型单变量数据分布图、连续型双变量数据分布图和连续型多变量数据分布图三个角度来一起学习。

单变量分布图

单变量其实就是我们通常接触到的数据集中的一列数据。在这里我们研究的是连续数值型数据的分布，那么什么样的数据是连续数值型数据呢？

连续变量的数值是连接不断的，相邻两值之间可作无限分割，例如，身高、体重、年龄等都是连续变量。

np.random.normal(loc=0,sigma=1,size)

normal会产生服从正态分布的size个数值，其中，loc表示均值，默认值为0，sigma是标准差，默认值为1，size表示产生的随机数的个数，即normal默认会产生服从标准正太分布的size个随机数，我们可以通过设置loc和sigma产生服从其他分布的随机数。

import numpy as np
#random是Numpy的一个‘随机’模块，在random模块中的normal方法表示从标准正态（高斯）分布中随机产生size个数值
data = np.random.normal(size=1000)
#查看数据类型
type(data)
#查看数据，查看数据的表现形式
data

import numpy as np
#random是Numpy的一个‘随机’模块，在random模块中的normal方法表示从标准正态（高斯）分布中随机产生size个数值
data = np.random.normal(size=1000)

type(data)

numpy.ndarray

data

array([ 1.07468886e+00,  1.64502509e+00,  3.48671115e-01,  4.70998213e-01,
        1.00921114e+00, -1.11691436e+00, -1.47920886e+00,  3.61852531e-01,
        9.75786773e-02,  4.78092188e-01, -1.35114529e+00, -6.73198925e-01,
        1.10916107e+00, -2.42504429e-01,  2.38748303e-01, -1.77929025e-01,
       -3.01001820e-01,  1.26160531e+00,  2.38760729e-01,  5.56291903e-01,
        6.93077065e-01,  8.47301758e-01,  1.25870160e+00, -6.88255411e-02,
        3.56453808e-01,  1.99727547e+00,  1.17297811e-01,  2.46691313e-01,
        3.97862526e-01, -7.98643043e-01, -8.04833248e-01, -4.84905695e-01,
       -7.16626369e-01,  7.90707582e-01, -2.55656699e-01,  1.23093744e+00,
       -1.03501205e+00, -1.53640346e+00, -1.51540477e+00, -2.31743510e-01,
        4.25501898e-01, -2.45176702e-01,  1.79412576e+00, -2.30862884e+00,
       -1.37842867e+00,  1.24879496e+00, -4.94991653e-01,  6.35373403e-01,
       -2.69511934e-01, -3.01055094e-01,  6.23279983e-01, -5.64989267e-03,
        1.75444983e-01,  1.27922022e+00,  8.79471084e-01,  5.02226492e-01,
        9.81643368e-01,  1.40139834e+00, -2.67207937e-01,  1.13968599e+00,
       -1.07046803e+00,  1.26124996e+00, -4.32011219e-02,  5.45190597e-01,
        3.97665923e-01, -1.46266220e+00,  5.78229049e-01,  1.61343838e+00,
        2.40367414e+00, -8.20872039e-01,  7.91718649e-01, -1.11690767e+00,
        8.09668999e-01, -1.12897624e-01,  1.48113899e+00, -6.98390420e-01,
       -4.64558205e-01,  8.50016747e-01,  2.16582474e-01, -5.64696344e-01,
        8.24602469e-01,  2.42888013e-01,  8.61869291e-01, -1.67639261e+00,
        2.37435182e-01,  6.13830388e-01,  2.84036290e-02,  1.21652072e+00,
        2.86267615e-01, -1.28228351e+00,  7.00447637e-01, -9.24361084e-01,
       -2.89248503e-01,  3.10497010e-01,  1.20324713e+00,  1.52198278e+00,
       -3.16429429e-02,  1.24812681e+00, -1.78804614e-01,  2.06167741e-01,
        1.49150248e+00,  6.76906388e-01, -1.30189128e+00, -3.13817980e-01,
        1.20376211e+00,  2.70930816e-01,  2.44903850e-01, -9.59090609e-02,
        1.36665130e+00,  9.57867712e-01,  9.49044254e-01,  6.40397238e-01,
       -1.87699456e+00, -6.22608146e-01,  1.71746810e-01, -4.62698718e-01,
        2.89748872e-01,  6.58019184e-01,  1.67657793e-01, -1.41661378e-01,
        1.57927732e+00,  2.17780503e+00,  2.00604221e-01,  2.26079241e-01,
        1.11989215e+00,  7.51289287e-01, -1.38876462e+00,  3.76618504e-01,
        1.11202534e+00, -1.04082431e+00, -1.79893046e+00,  1.11810846e-01,
        5.53264381e-01,  1.30854242e+00, -2.88210592e-01,  7.18931374e-01,
       -1.60241542e+00, -2.05652838e+00,  7.19852250e-02,  7.70611798e-01,
        1.74965317e+00, -7.03094173e-01, -2.65978786e-01, -9.89226065e-02,
       -1.19615409e+00, -2.03953500e-01, -1.67983865e+00,  1.44769063e+00,
        4.20862400e-01,  3.22138778e-01, -1.30708430e+00,  9.70172532e-01,
       -1.54775280e+00, -3.69683643e-01,  1.83421557e+00, -9.26829730e-01,
        5.60121269e-01, -3.65085256e-01,  2.33743720e+00,  2.22667012e-01,
       -2.98366761e-01,  7.13110554e-02, -3.92737472e-01, -3.63772583e-02,
        1.64669993e+00, -1.10370983e+00,  8.46386336e-01, -7.84900100e-01,
       -8.39703252e-01,  5.46016037e-01,  2.48213796e-01,  5.64454402e-01,
        1.98542179e+00,  8.85916558e-01,  5.05093948e-01,  3.47996041e-01,
       -9.18070791e-01,  4.89836843e-01, -3.09975781e+00,  3.04039913e-01,
       -1.03743875e+00,  6.70219424e-01, -1.72976760e+00,  2.00645372e+00,
        7.13266796e-02,  6.29599715e-01, -1.80107552e-01,  1.68905992e-01,
        1.36405988e+00,  1.06954157e+00,  1.37672136e+00,  7.84980043e-01,
       -6.73012312e-01,  4.40055208e+00, -1.88486950e+00,  9.98108899e-01,
       -1.03823999e+00, -2.55788421e-01, -1.76312588e-02,  7.37613125e-01,
        7.91996111e-01, -1.31438976e-01, -2.82801928e-01,  4.08797728e-01,
       -2.06032814e-01,  6.56852392e-01, -3.76084481e-01, -1.12457613e-01,
       -9.72301309e-01,  2.47112990e-01,  2.06275042e+00, -8.15507807e-02,
       -5.59188818e-01, -9.10864888e-01,  1.44023727e-01,  3.85115457e-01,
       -4.39665507e-01, -1.41920427e+00, -6.69435525e-01,  4.91578827e-01,
        7.13421263e-01,  1.73081627e+00,  6.13225251e-01,  2.32079052e-01,
       -1.05349582e-02,  7.10323974e-01,  3.18361084e-01,  2.40560050e+00,
        4.21197209e-01, -1.05564688e+00, -4.25235431e-01, -2.25511254e-01,
       -2.85498977e-01, -8.92657987e-01,  1.07288885e+00,  1.48463694e+00,
       -2.16786004e-01,  4.64472009e-01,  1.30977710e+00, -1.32461991e-01,
       -5.26196103e-02, -1.95507709e+00, -1.82299958e+00,  6.39921196e-01,
        1.98345525e+00,  9.62458707e-01, -9.61797000e-01, -3.75501132e-02,
        1.42994148e-01,  8.85354139e-01,  7.56009171e-01,  1.11459755e+00,
        5.69345686e-01, -3.52713453e-01, -1.08155913e+00, -8.96122517e-01,
       -4.52194531e-01, -1.20089822e+00, -8.17647473e-01,  5.64667489e-01,
       -1.76360713e-01, -8.13488635e-01,  9.04655187e-01,  4.00766089e-01,
        1.22855456e+00,  8.59980770e-01, -1.30982823e+00, -7.85052046e-02,
       -9.82837313e-02,  3.60376219e-01,  2.15153930e-01,  3.33051806e-01,
       -9.14559377e-01, -8.64619436e-01, -8.60684780e-01, -3.32368979e-01,
       -1.24498739e-01,  5.90624549e-01,  1.07763124e+00, -1.57964957e+00,
        9.32674129e-01,  1.29795126e+00,  2.38657295e-01,  8.94782839e-01,
        6.13934113e-02,  1.53025564e-01, -1.06378806e+00, -6.11276255e-01,
        1.36960968e+00, -3.04788827e-02, -2.08338410e-01,  1.54983822e+00,
        3.63288807e-01, -1.68826842e+00, -2.51625368e+00,  2.74906073e-01,
       -6.35164706e-01,  5.84221931e-02, -6.13513633e-01,  1.39296326e+00,
       -4.21627803e+00, -8.60951646e-01,  8.57217601e-02,  3.41756688e-01,
        1.54102414e+00, -9.69425965e-01, -1.55957650e+00, -8.05632987e-01,
        3.81575247e-01,  1.82262060e-01, -6.82924185e-01, -1.68306717e+00,
        1.33462425e-01, -3.03576381e-01,  1.37861481e+00,  9.28527042e-01,
       -2.66738677e-01, -2.13283715e+00, -1.83573471e+00, -5.79633944e-01,
        1.05269840e+00,  4.62588407e-01,  5.87509461e-01,  4.91406483e-01,
       -1.51035276e+00, -1.06192252e+00,  7.42228906e-01,  1.42500860e-01,
       -2.13679519e+00, -6.52752110e-01,  5.01474753e-01, -1.10020580e+00,
       -5.18589770e-01,  6.28931989e-01, -8.40986046e-01,  9.69755539e-01,
        7.87214770e-02,  8.98987673e-02,  5.05619856e-01,  1.21220619e+00,
       -1.62199252e+00,  7.78747779e-01, -1.70880787e+00, -4.43955797e-01,
        8.25197366e-02,  1.64745583e-01, -1.80090394e+00, -2.09465258e-01,
        1.11573590e+00, -2.03889138e-01,  1.64367042e-01,  8.44568739e-01,
       -2.08338445e+00, -1.90294226e-01,  2.07055498e+00,  2.20238461e+00,
       -7.15648379e-02,  1.12474069e+00,  8.65233735e-01,  2.75349612e-01,
       -1.59865401e-01,  7.81464708e-01, -1.42487197e+00,  9.94515278e-01,
        9.27864011e-02,  2.13084115e+00, -1.42375212e+00, -6.73944748e-01,
        4.11900972e-01, -4.93938673e-01,  2.96923115e-01,  8.96341546e-01,
        1.31678933e+00, -1.43338778e+00,  8.78567520e-01, -1.52467125e+00,
        1.24807274e+00,  1.81553037e-01, -4.51181175e-01,  1.24464866e+00,
       -1.04805214e+00, -8.61982093e-01,  2.59430150e-01,  5.81207003e-01,
        9.48077003e-02,  1.54388981e-01,  5.91514771e-02, -1.15679562e+00,
       -2.18302039e+00, -1.32503181e+00,  2.84610145e-01,  2.51808133e-01,
        3.21259610e-01,  8.74239199e-01, -7.50299693e-01,  6.56494246e-01,
       -4.95960739e-01, -1.60090293e+00, -1.10433011e+00, -4.23640838e-01,
        1.06180396e+00,  2.01837772e-01, -6.81962545e-02, -1.43047762e+00,
        4.74002813e-01, -1.67268525e+00,  3.98695794e-01, -1.90132490e-01,
        4.36551721e-02,  1.20992723e+00,  2.32822123e+00,  1.04786286e+00,
       -6.71335104e-01, -2.04204743e-01,  1.04612535e+00, -4.90743231e-01,
       -8.29692900e-01,  6.70046302e-01,  8.03443573e-01, -5.05952025e-01,
        1.27770544e+00,  1.28469436e+00,  1.08530547e+00,  1.57902610e+00,
       -7.66819889e-01, -1.25242207e+00, -5.90427323e-01,  3.04917356e-02,
       -3.87884448e+00, -5.25332631e-01, -2.28250545e+00, -5.71806038e-01,
       -3.03670952e-01,  1.39324233e+00,  1.82412726e+00,  4.27052652e-01,
        6.34184083e-02, -4.50138497e-01,  2.30833592e+00,  2.39976295e-01,
        5.03874648e-01, -4.19689247e-01,  6.43927329e-02,  6.15554034e-01,
       -3.54346963e-01,  2.46362627e+00,  6.24975354e-01, -3.79988320e-01,
       -1.07418266e+00, -1.10849556e+00,  2.72256056e-01, -4.02720649e-01,
       -1.42947627e+00,  3.34886484e-01,  1.43359160e+00, -1.01869637e+00,
        6.26283230e-01,  8.37772560e-02,  4.01825213e-01, -1.13450592e+00,
        1.11693554e+00, -3.67633794e-01, -8.24072446e-01,  7.71782986e-01,
       -7.75554557e-01, -1.28800142e+00, -7.74139720e-01, -5.66985312e-01,
        6.41859556e-01, -1.50011214e+00, -9.45900971e-01,  1.82131334e-01,
        4.54014638e-02, -5.87737629e-01,  4.48221894e-01,  6.73608053e-01,
       -1.39246101e+00,  1.01668368e+00, -5.04620692e-01, -1.81629759e+00,
        9.87588234e-01,  1.01676842e+00,  2.47657227e+00,  3.93887127e-01,
       -1.04259472e+00, -1.11382383e+00, -2.14859590e+00, -4.08593681e-01,
        5.20950433e-01, -1.00320352e+00,  6.50083967e-01, -2.33606740e-02,
       -1.57675708e-01,  4.68014020e-02, -1.49217828e+00, -1.62683086e+00,
        8.58416223e-01,  9.75051581e-01, -4.34300842e-02,  3.58005708e-01,
        5.48749392e-01, -5.29636582e-01, -5.74412560e-01, -8.28687365e-01,
        7.20369966e-01, -1.42927185e+00,  1.03023391e+00, -8.06507970e-01,
        2.04500824e-01, -6.66037069e-01,  9.65282632e-02, -4.88145952e-01,
       -4.26628399e-01,  5.91443526e-01, -8.61621862e-01, -1.82074802e-01,
       -3.35358438e-02,  1.92476658e-01,  1.13838480e+00, -1.26149601e+00,
        8.50599236e-02, -2.34269915e-01,  1.34799604e+00, -4.32761743e-01,
       -9.50909374e-02, -9.30829553e-01,  3.02791233e-01,  1.12285184e+00,
        3.57865090e-01,  1.25725091e-01, -1.07432107e+00,  1.50482319e+00,
       -7.95127879e-01,  1.20948106e+00, -1.93729329e+00, -3.29101678e-01,
        1.18603496e-01,  1.19598774e+00, -6.99046460e-02,  4.51415782e-01,
        7.33644225e-01, -1.21836951e-01,  8.69511759e-02, -1.86199497e-01,
        8.52930459e-01,  3.93739552e-01,  3.70237460e-01,  2.48352575e-01,
        1.84570817e-01,  5.43843348e-01,  1.13650963e+00,  1.66296651e+00,
       -1.62904298e+00,  2.90543750e-01, -2.46653511e-01,  5.68835949e-01,
       -1.46110167e-01, -7.25050350e-01,  2.12214264e-01,  7.84099043e-01,
        9.77717406e-01, -6.52487622e-01,  1.03921394e+00, -6.56641875e-01,
        5.93594520e-02,  6.07056272e-01, -4.20230033e-01, -7.47631356e-01,
        1.81532063e-02, -5.01966548e-01,  3.94528107e-01,  4.21122442e-01,
        1.40257064e+00,  3.41791437e-01, -1.08325357e-02, -4.33397159e-01,
       -7.93161339e-01, -1.33577362e+00, -8.47207543e-01, -4.93381215e-01,
        2.43824864e+00,  9.24984035e-01,  3.58179994e-01, -2.99747175e-01,
        5.16587667e-01, -9.12512032e-02, -4.16334599e-01, -2.11155435e+00,
        2.36672420e+00, -1.19301734e-01,  4.74198036e-01, -1.27327328e+00,
        1.74604160e+00,  8.32062014e-02,  1.00294757e+00,  8.72393928e-01,
        5.54866670e-01, -1.30827188e-01, -5.88156238e-01,  6.50563850e-01,
       -5.77132994e-01, -3.10905099e-01, -7.21578379e-02,  6.58795991e-02,
       -3.61472122e-01,  2.35582031e-01, -1.45559683e-01,  1.26964311e+00,
       -1.82203846e+00, -1.35167964e+00, -7.16485050e-02,  1.12511769e+00,
       -2.32434631e-01,  1.46337341e+00, -3.33367592e-01, -3.72374637e-01,
        7.06525432e-01,  1.23160654e+00, -2.56006272e-01, -6.66452397e-02,
       -1.52708857e+00,  2.10765211e-02,  3.95237976e-01,  1.33075357e+00,
       -1.31069864e+00, -2.13423249e+00, -1.07817424e+00, -4.51129173e-01,
        5.73573908e-01,  2.39343326e-01, -8.16266733e-01,  6.73697683e-01,
       -1.22307320e-01, -1.66548728e-01, -7.27865865e-01, -5.30136511e-01,
        1.72466364e+00, -3.01759098e-01, -5.41144307e-01,  4.65553126e-02,
       -1.05400475e+00,  5.43867102e-01,  1.27295542e+00,  7.83244539e-01,
        1.15915325e-02, -9.99321000e-01,  5.11089970e-01,  7.09752016e-01,
       -2.67909091e-01,  1.34481940e+00, -3.34951140e-01,  3.27941684e-01,
        9.10422933e-01, -9.15702467e-01,  3.16255193e-01, -7.15958230e-01,
       -8.42515872e-01, -1.21033761e+00,  6.54520503e-01,  9.96160081e-01,
        7.72702243e-01, -2.34419423e-01,  5.80625796e-01,  3.88740878e-01,
       -7.96458163e-01,  1.09514844e+00,  1.60019454e-01, -3.72763020e-01,
       -1.52953866e+00, -5.07967496e-01, -8.99213158e-02, -6.18542157e-01,
        1.16100655e+00,  7.87712097e-01,  2.19377135e+00, -1.79418384e-01,
       -1.13572611e+00, -1.63012084e+00, -1.18571850e+00, -1.50870048e+00,
        4.21595470e-01, -2.17057240e-01,  1.65898452e+00,  1.09095850e+00,
        8.66717036e-01, -5.98408583e-01, -1.17043655e+00, -1.24735558e+00,
       -1.49893409e+00,  1.32307005e-01,  2.05790963e+00,  1.01271953e+00,
        6.34178161e-01,  4.47223607e-01,  4.08235391e-01, -8.89309692e-02,
       -3.93188987e-01, -1.19629954e-01,  1.28525627e+00, -9.70423494e-01,
       -1.60648087e+00,  1.26153270e+00, -4.83065010e-01, -4.08487151e-01,
        2.19421293e-01,  9.98135510e-01, -2.74223871e-01, -9.34105697e-01,
        6.93820589e-02, -2.92029858e-01, -1.53506325e-01, -3.81470957e-01,
        1.81768309e+00,  4.52269885e-01,  9.15031455e-01,  6.07074757e-01,
       -1.40887303e+00, -1.38290758e+00, -1.90743247e+00,  8.64645361e-01,
        1.39543087e-01,  4.04759262e-02, -4.49256612e-01, -1.20951769e+00,
       -4.74546987e-01, -9.94208778e-01, -4.63662116e-01, -6.67522974e-01,
        7.39007304e-01,  2.27493561e+00, -1.11739468e+00,  8.69128844e-01,
        5.64101847e-01, -7.69571239e-01, -3.34391040e-01,  4.86383282e-01,
       -1.72983612e+00,  8.35059058e-01, -1.19481110e-01,  1.70935135e+00,
        8.56433085e-01,  2.12670893e-01, -4.63162795e-01, -2.99699959e-01,
       -6.92497862e-01,  4.53952793e-01, -4.85359637e-01,  8.26367397e-01,
        2.38946271e+00,  3.13984122e-01,  8.38096118e-01, -1.03554985e+00,
        1.03217431e+00,  1.39600471e-01, -1.48596672e-02,  8.82515651e-01,
        1.10199188e+00, -1.53763940e+00, -1.84236037e+00,  1.44862762e-01,
       -3.74739743e-01, -6.58717620e-01, -4.53126107e-01,  2.74691270e-01,
        3.53751523e-02, -1.31223563e+00, -2.18605800e-01, -3.87197693e-01,
        5.20866063e-01,  1.11134754e+00, -1.84809352e-01, -5.66080422e-01,
        1.07900575e-01,  5.61355190e-01,  6.92638845e-01,  2.31990760e-01,
       -1.60954979e+00, -1.92436816e+00, -1.50876258e+00, -1.49663763e+00,
       -2.68855577e+00,  6.78238213e-01, -8.10679976e-01, -3.83130104e-01,
        1.54695763e+00,  3.60861746e-01,  1.47013088e+00, -2.03872975e+00,
        9.11112667e-01, -3.88961269e-01,  3.15828241e-01, -1.16656854e+00,
        6.96258941e-01, -1.43240209e+00,  1.03631325e+00,  8.41127954e-01,
        1.43763517e+00, -5.93108035e-01,  2.48515973e-01, -2.00983741e+00,
       -3.44017809e-01, -8.81222692e-01,  2.71098848e-01,  3.37327147e-01,
       -6.46748582e-01,  1.38308958e+00,  1.22846816e+00,  9.12808431e-01,
        2.78275592e+00, -1.75597222e+00,  2.54009155e-01, -2.04791701e+00,
        4.47188076e-02, -1.09645652e+00, -2.37489717e-01,  1.21847238e-01,
        4.77672084e-01, -1.63235500e+00, -1.57313580e-01,  4.10974737e-02,
        2.94635030e+00, -7.32966013e-01, -4.65392571e-01,  6.71379377e-01,
       -5.55238688e-01,  9.85126503e-01,  2.41486299e-01,  3.54358465e-01,
        1.40885702e-01,  1.53358769e-01,  4.18706008e-02, -2.72112959e-01,
        1.42754161e+00, -2.69839930e+00,  3.47279173e-01,  3.04460030e-01,
        2.62166028e-01,  4.30206354e-01, -4.24172166e-01,  8.64177526e-01,
        1.67305078e-01, -2.79759543e-01,  9.16665679e-01, -1.97100088e-02,
       -5.63670054e-01, -7.45228584e-01, -1.69776998e-02,  1.51493449e+00,
        3.15501397e-01, -1.92619231e+00,  6.60943755e-02,  3.70467478e-01,
        5.26283472e-01, -1.01462031e+00,  7.78895937e-01, -1.56376583e+00,
        2.72471896e-01,  1.40515017e+00,  2.11943187e-01,  1.54756599e+00,
       -4.65575109e-01,  6.00404067e-01,  6.62880198e-02, -5.62735611e-01,
       -4.99214101e-01,  1.84008223e+00,  6.79941559e-01, -1.24347827e+00,
        2.99816390e-04, -2.39655811e-01, -3.78113791e-01,  1.02694199e+00,
       -4.82559879e-02, -2.76438701e+00,  1.02277794e+00,  1.08577688e+00,
       -6.85545777e-01, -6.98942978e-01, -1.12585137e+00, -1.85512534e-01,
       -7.96771204e-01, -7.42094643e-01, -9.81699460e-01, -2.41053479e+00,
       -2.46247204e-01, -1.01795472e+00, -8.63179663e-01,  1.12996278e+00,
       -1.03899770e+00, -2.38357605e+00, -2.88512915e-01, -3.46505612e-01,
        8.84032576e-01,  9.97070232e-01,  2.34367703e+00,  1.59633453e+00,
       -1.08672000e+00, -4.23972145e-01, -2.36479584e-01, -4.05166617e-01,
       -2.66984301e-01, -1.14776245e+00,  4.87349098e-01, -1.61571852e-02,
       -1.61580019e-01, -1.33509897e+00,  1.65015731e+00,  3.22551627e-01,
       -9.97476130e-02,  3.92936183e-01,  6.12405681e-01,  1.68351773e+00,
       -5.91078027e-01, -1.75439240e+00, -8.09012289e-01,  1.13994951e+00,
        3.66420375e-01, -3.05862292e-01, -1.08963567e+00, -2.87309680e-01,
        5.83249809e-01, -1.83046610e-02, -4.06233549e-02,  9.63431771e-01,
       -1.18197012e+00, -3.44438577e-02,  3.04771315e-02, -1.32882181e+00,
        1.03426569e+00,  5.21717495e-01,  4.91118502e-01, -1.16084440e+00,
       -5.94570657e-03, -3.26201262e-01,  9.78908188e-01, -8.83709685e-01,
        9.01140106e-01, -6.91337805e-01,  8.12713840e-02, -8.12702412e-01,
        1.18174667e+00, -4.26553536e-01,  2.47130199e+00,  1.52710753e+00,
       -6.59286546e-01,  7.58632243e-01,  2.84049593e-02,  1.40328864e+00,
       -1.19049079e+00, -2.16772936e+00, -2.25448930e-01, -1.00572107e+00,
       -5.78376477e-01,  5.70841962e-01, -5.10209967e-01,  1.55105293e+00,
       -6.59264906e-01,  3.89461999e-01, -1.51883591e+00,  1.53581999e+00,
        1.24123633e-02,  1.15551101e-01,  1.22226025e+00,  5.11958484e-01,
        7.24079528e-01, -1.49753722e-01,  1.46665055e+00, -1.39547443e+00,
       -2.84709791e+00, -7.88756688e-01,  1.84675889e-02, -5.97256779e-01,
        1.27506723e+00,  5.83123571e-02,  9.47334881e-01,  2.70326143e+00,
        5.07364045e-01, -1.32248663e+00, -5.97394033e-01,  1.08267355e+00,
        2.05076222e+00, -1.39356318e+00,  7.77294976e-01, -5.92320133e-01,
        1.10629864e+00, -1.69450086e-01,  6.69170886e-01, -1.29831709e+00,
       -1.51813654e+00,  7.51894893e-02,  6.50619362e-04,  8.26747723e-01,
       -1.39653009e+00,  7.17723640e-01, -7.85821700e-01, -7.32052323e-01,
        1.31095593e+00,  1.12107836e-01,  1.16008760e+00,  1.98142962e+00])

size=1000，表示随机产生1000个数，它们组成的数据是一组连续型的数值型数据。

问：老师，NumPy库是什么？random又是什么哈？
答：NumPy是一种科学计算库，是Pandas的基础库，也可以对数据进行向量化操作，以及运算，random是NumPy的一个模块，它包括了很多的随机方法，这里我们主要用来产生随机数。

NumPy的数据对象一般是ndarray类型的，通过type方法，可以发现data数据的类型为ndarray类型。通过打印数据data，可以发现数据表现形式是array( )。

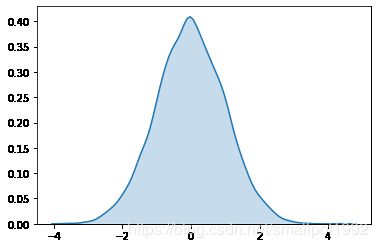
对于一组连续数值型数据，根据绘图函数内置的核函数计算数据的概率密度，用一条曲线将数据拟合出来，从而描述数据的分布。比如，对于标准正态分布：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hmVrNvp4-1587694107657)(标准正态分布.png)]

横轴表示数据点的取值，纵轴表示概率密度值。

出现次数较多的数值区间，相对应的概率密度也会大一些，在数字0周围，概率密度值是最大的。随着向两侧的逐渐扩展，概率密度逐渐减小，这样的分布就是一个标准正态分布。这条曲线也叫做概率密度曲线，而绘制的整个图通常叫做核密度估计图。

在Seaborn中绘制概率密度曲线，我们使用 sns.kdeplot( )，绘制得到的图像叫做核密度估计图。

下面我们就来绘制刚刚生成的1000个数据的核密度估计图，看看它们是否可以很好地拟合正态分布曲线。

sns.kdeplot()函数的使用方法如下：

sns.kdeplot(data1,data2,shade=False)

data1和data2参数分别为绘制图像用到的数据，如果绘制单变量数据，只传入一个参数就好，得到概率密度曲线图。

shade参数用于设置图像下方的部分是否设置阴影，默认值为False，表示不绘制阴影。

#data核密度图
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
%matplotlib inline
#从标准正态分布中生成1000个数
data1 = np.random.normal(size=10000)
sns.kdeplot(data1,shade=True)
plt.show()

图像近似服从标准正态分布，但是还是有一些误差，大家可以在代码中尝试生成更多的数据或者减小数据量，来观察随着数据量的增多，图像的拟合程度是如何变化的。

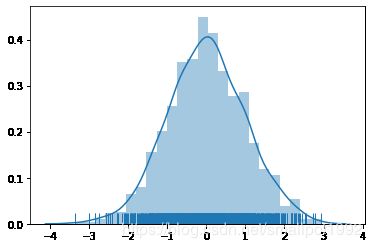
在上一关中我们学习到对于连续数值型单变量数据，可以使用直方图描述数据的分布：将数据分成若干个组，用柱形的高度记录每组中数据量的大小。

在Seaborn中，distplot()集合了matplotlib 的 hist() 与核密度估计kdeplot()的功能。

sns.distplot(data,bins,hist=True,kde=True,rug=False)

data参数记录绘图所用的数据，而bins参数在绘制直方图时可以进行设置，用于设置分组的个数，默认值时，会根据数据的情况自动分为n个组，若是想指定分组的个数，可以设置该参数，然后计算我们可以增加其数量，来看到更为详细的信息。

hist和kde参数用于调节是否显示直方图及核密度估计图，默认hist、kde均为True，表示两者都显示。我们可以通过修改参数为False选择是否将其中之一去掉。

由于直方图只能将取值区间划分成不同区域之后以区域小条的面积表示数据频数，并不能表达具体数据出现在什么点上。distplot()方法提供了rug参数，默认值为False。当设置为True时，表示在图的下边沿用细条绘制每个观测数值的位置，它被叫做边际毛毯。

下面我们就来给刚刚生成的1000个数据绘制distplot。请大家完成以下代码，按照老师的指引，在#TODO的部分填充所需的代码即可。

import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
%matplotlib inline

data1=np.random.normal(size=1000)

#绘制distplot,设置参数，使得直方图和核闭幕估计图都显示，显示边际毛毯
sns.distplot(data1,rug=True)
plt.show()

通过观察我们绘制的图像，发现直方图和核密度图绘制在了同一个画布上，有同学可能想，我想使用这个方法只绘制核密度图或者直方图，该怎么做呢？ 按照下列的参数设置，我们可以只绘制直方图，或者只绘制核密度图。

#distplot不显示直方图或核密度图
import seaborn as sns
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
#从标准正态分布中生成1000个数
data1=np.random.normal(size=1000)

#只显示核密度图，设置distplot中的参数，使得图像中不显示直方图
sns.distplot(data1,hist=False)

#只显示直方图，修改distplot中的参数，使得图像不显示kde图像
sns.distplot(data1,kde=False)

#连续单变量卡路里含量的分布图
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
menu=pd.read_csv('menu.csv')
plt.figure(figsize=(10,5))
#选取menu数据集中的Calories列，将数据记录为calories
calories=menu.Calories

#绘制displot,同时显示直方图和kde曲线，边际毛毯参数设置为True
sns.distplot(calories,rug=True)
plt.title('麦当劳菜单卡路里含量分布图')
plt.show()

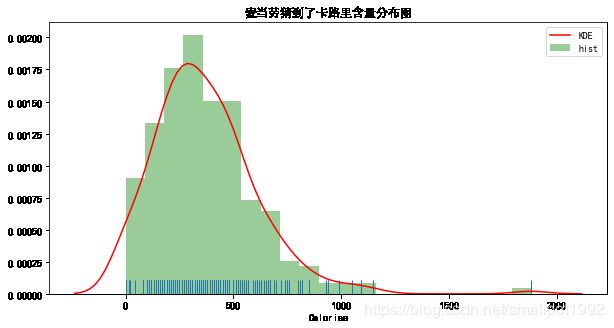
当然，在distplot中，除了控制矩形分布、密度曲线及边际毛毯是否显示之外，我们还可以通过更丰富的参数调整图像的显示细节，例如我们可以通过hist_kws 、kde_kws参数来设置图像的图例信息，这两个参数使用字典的方式实现多个功能。

请大家在distplot中添加这样两个参数，来看一下返回结果：

hist_kws={'color':'green','label':'hist'}, kde_kws={'color':'red','label':'KDE'}

# 连续单变量卡路里含量的分布图图例
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
menu=pd.read_csv('menu.csv')
plt.figure(figsize=(10,5))
calories = menu.Calories

sns.distplot(calories,rug=True,hist_kws={'color':'green','label':'hist'},kde_kws={'color':'red','label':'KDE'})

plt.title('麦当劳猜到了卡路里含量分布图')
plt.show()

我们看到hist直方图显示为绿色，ked曲线显示为红色。在图像的右上方标注了两种图形的形状、颜色和图像名称。

这就是连续数值型单变量数据常见的可视化方法，我们常会使用到直方图、核密度图来描述数据的分布。在Seaborn中也集成了这两种图像，使用distplot可以将它们绘制在同一张图中。

双变量联合分布图

刚刚我们学习的是基于单变量的数据可视化。而在实际问题中，我们遇到的数据往往比较复杂，而且我们不仅仅只需要对数据进行观察，往往还需要进行预测等。那么数据之间关系的分析就显得非常重要了。

在这一节中我们开始对连续型数据之间的关系进行分析，我们先来看一下连续数值型双变量之间的可视化方法。

可视化连续型双变量时，我们往往会用两条垂直的坐标轴表示其中的一个变量数据，将数据绘制在一个二维坐标系中。

在Seaborn中绘制连续数值型双变量我们使用sns.jointplot():

sns.jointplot(x,y,data,kind)

参数x、y分别记录x轴和y轴的数据名称，这两组数据都来源于data数据集，data的类型为DataFrame，kind参数用于设置图像的类型，可选的类型有：‘scatter’ | ‘reg’ | ‘resid’ | ‘kde’ | ‘hex’，分别表示散点图、回归图、残差图、核密度图和蜂巢图。

双变量联合散点回归图

如果两个变量都是连续型变量，我们希望看一看在二维平面上二者之间的关系，那么首先想到的应该就是散点图。散点图可以帮助我们很容易地发现一些数据的分布规律。

sns.jointplot()函数可以显示两个变量之间的联合关系以及每个单变量的分布和轴。

我们把函数中的kind参数设置为’scatter’，就可以绘制双变量散点图，如果设置为’reg’就可以做一些简单的线性模型拟合。

现在我们创建一个含有两列数据的DataFrame，每列数据为从标准正态分布中抽取的500个数字。然后绘制双变量分布回归图。

np.random.randn(d)

randn和normal类似，也是产生服从标准正态分布的若干随机数。But，不同点是，randn默认产生服从标准正态分布的随机数，且不可以设置均值和标准差，但是，normal可以设置均值和标准差，产生服从正态分布的随机数。

#双变量分布回归图
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
#创建dataframe:df
df = pd.DataFrame({'x':np.random.randn(500),
                  'y':np.random.randn(500)})
#绘制双变量分布回归图，x，y参数分别为df的列名称，主义列名称用字符串的形式
#kind参数设置为reg，表示绘制回归图
sns.jointplot(x='x',y='y',data=df,kind='reg')
plt.show()

在图中绘制了x和y数据的散点图；以及数据的拟合回归直线图，直线周围的阴影是误差范围，参数ci表示置信水平，用来控制这个误差范围，ci参数的默认值是95，也可以设置其它的置信水平来绘制回归直线图；在坐标系的上方和左侧分别绘制了两个变量的直方图和核密度图。

双变量联合蜂巢图

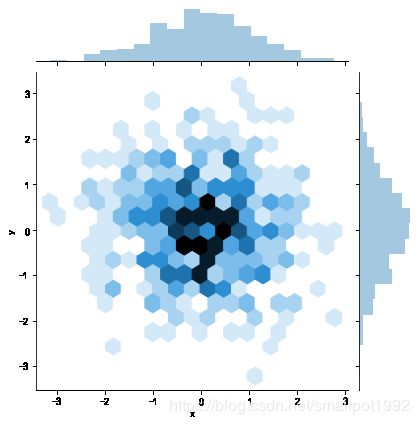
Hexbin图也叫做蜂巢图，它可以更加直观炫酷地看出数据的分布情况，我们先来看看它长什么样吧。

请将kind参数修改为hex来运行一下代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
df = pd.DataFrame({'x': np.random.randn(500),
                   'y': np.random.randn(500)})

sns.jointplot(x='x',y='y',data=df,kind='hex')
plt.show()

图中显示了六边形仓内的观测数，颜色越白的地方数据量越小，落在该区域的数据较少；颜色越深的地方表示数据量越大。

这样的图适用于较大的数据集。可以直接根据颜色区分数据的密集程度。

双变量联合密度图

描述数据的密度我们还可以使用在上一节中学习到的kde核密度图。我们把kind参数设置为kde，来看看它的效果。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
df = pd.DataFrame({'x': np.random.randn(500),
                   'y': np.random.randn(500)})
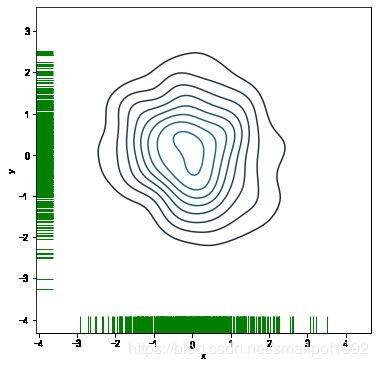
sns.jointplot(x='x', y='y', data=df, kind='kde')
plt.show()

核密度曲线用封闭的不规则图形（类似于等高线）表示。同样，颜色较深的区域表示数据密度较大，颜色越浅表明数据密度越小。

在上一节学习sns.kdeplot()函数的时候，我们介绍过函数的常用参数主要有：

sns.kdeplot(data1, data2, shade = False)

在介绍单变量分布图的时候我们只带领大家练习了传入一个data时的可视化方法。其实，sns.kdeplot()也可以绘制双变量核密度图，结合地毯图sns.rugplot()，我们可以这样实现：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.figure(figsize = (6,6))
df = pd.DataFrame({'x': np.random.randn(500),
                   'y': np.random.randn(500)})
sns.kdeplot(df.x,df.y)
sns.rugplot(df.x,color='g')
sns.rugplot(df.y,color='g',vertical=True)
plt.show()

中间的封闭曲线是根据kdeplot绘制的双变量核密度分布曲线，而轴上的绿色竖条是由rugplot绘制的地毯图，表示数据的频率分布。

这样我们也可以得到数据分布的核密度图和频率分布观测条图。但是步骤就会略多一些，大家可以选择自己喜欢的方法来绘制数据分布图。

多变量关系分布图

通常情况下，我们在做数据分析时面对的数据集中往往有很多列连续型数据，在我们还没有确定针对哪两个变量进行挖掘的时候，比较严谨的做法是把数据集中每两列都考虑一次，做一个完整的变量关系可视化，而不是随便挑两列。

那么这个时候，我们就会使用连续数值型多变量关系分布图。绘制这样的图像，我们使用sns.pairplot()函数：

sns.pairplot(data,hue,vars,kind,diag_kind)

data表示绘图所用到的数据集，hue参数表示按照某个字段进行分类，vars参数可以用于筛选绘制图像的变量，用列表的形式传入列名称。

kind参数用于设置变量间图像的类型，可以选择’scatter’散点图，或者 'reg’回归图。

diag_kind用于设置对角线上的图像类型，可以选择’hist’直方图， 或者’kde’核密度图。

绘制多变量关系分布图，我们使用一个非常经典的数据集：鸢尾花数据集。首先来读入并查看一下数据集的内容详情：

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
data = pd.read_csv('iris.csv')
data.head()

	sepal_length	sepal_width	petal_length	petal_width	species
0	5.1	3.5	1.4	0.2	setosa
1	4.9	3.0	1.4	0.2	setosa
2	4.7	3.2	1.3	0.2	setosa
3	4.6	3.1	1.5	0.2	setosa
4	5.0	3.6	1.4	0.2	setosa

数据集中的每一列分别记录：

• sepal_length：花萼长度
• sepal_width：花萼宽度
• petal_length：花瓣长度
• petal_width：花瓣宽度
• species：花朵种类

数据集中前四个变量都是连续型变量，第五个变量species是一个分类变量。

那么我们就来使用pairplot查看一下数据集中的每两个连续型变量的分布图吧。

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
data = pd.read_csv('iris.csv')
# TODO
# 只根据数据集data绘制pairplot，且不设置其它参数
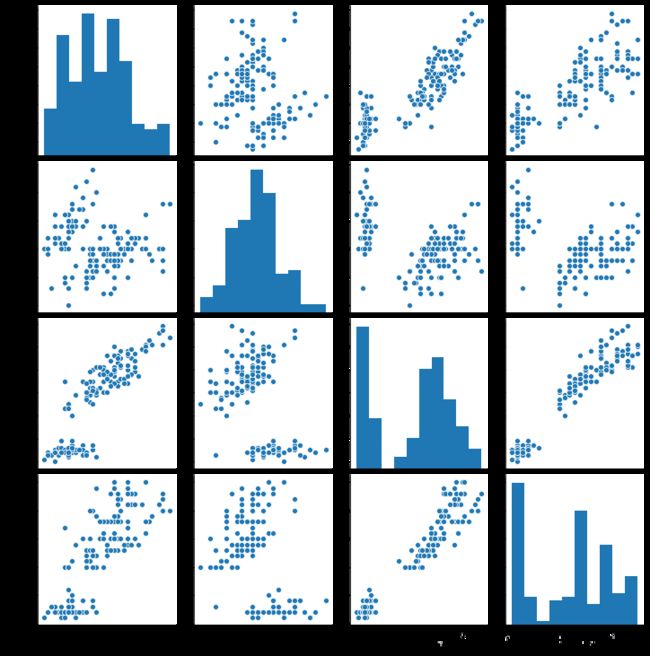
sns.pairplot(data)
plt.show()

从变量间的散点图我们可以看到：在petal_length和petal_width散点图中，数据点大致分布在一条直线上，呈现了比较明显的线性关系。

接下来我们将分类变量species考虑在图中，看看不同类别的鸢尾花的数据有没有明显的差别。

我们将hue参数设置为species。复制并运行这样的代码：

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
data = pd.read_csv('iris.csv')
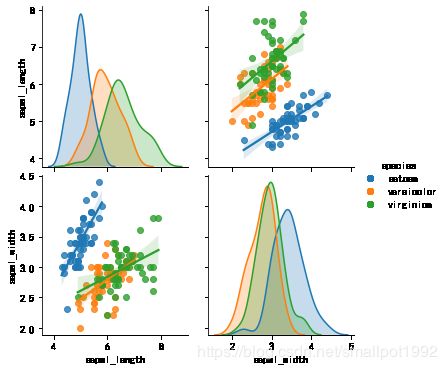
sns.pairplot(data, hue='species')
plt.show()

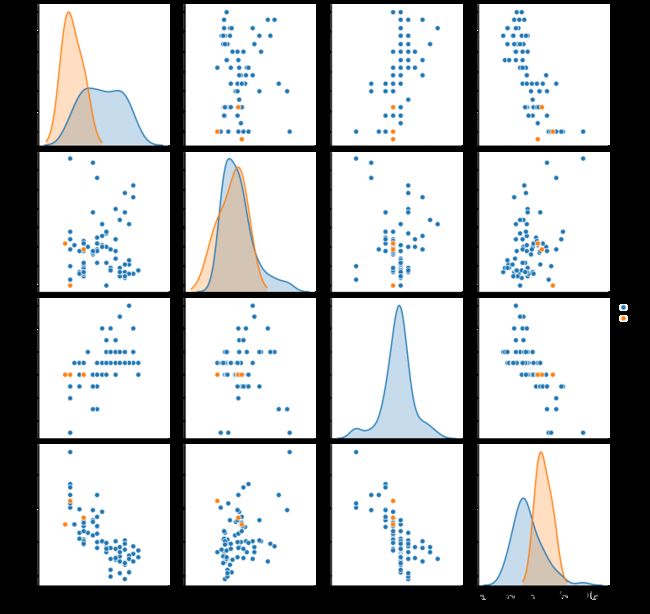
iris.csv是鸢尾花的数据集，它包含了三种花的数据，记录了每种花的花瓣和花萼的长度和宽度。在图中，分别以不同的颜色表示了这三种花，三种花的花瓣的长度和宽度，和花瓣的长度和宽度比较可以聚集为3簇，表示三种花有明显的差别。

那么接下来我们筛选出分类关系不是很明确的’sepal_length’, 'sepal_width’两个变量，来绘制这两个变量的pairplot。

# 多变量分种类关系分布图筛选变量
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
data = pd.read_csv('iris.csv')

# TODO
# 绘制'sepal_length', 'sepal_width'变量pairplot，并显示花朵分类
# 同时双变量图像设置为回归图，单变量（对角线图）设置为核密度图
sns.pairplot(data,hue='species',vars=['sepal_length','sepal_width'],kind='reg',diag_kind='kde')
plt.show()

我们再回到麦当劳菜品营养成分的数据集中，选择几个感兴趣的变量绘制它们的pairplot。

我们选择变量：‘Calories’,‘Total Fat’,‘Cholesterol’,‘Sodium’,‘Carbohydrates’,‘Sugars’,‘Protein’

# 麦当劳多变量关系分布图筛选变量
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

menu = pd.read_csv('menu.csv')

# TODO
# 绘制变量 'Calories','Total Fat','Cholesterol','Sodium','Carbohydrates','Sugars','Protein' 的pairplot

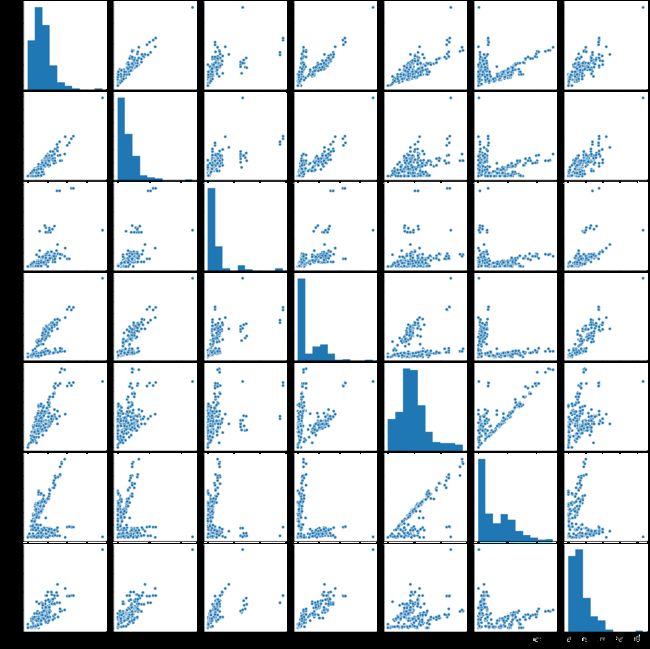
sns.pairplot(menu,vars=['Calories','Total Fat','Cholesterol','Sodium','Carbohydrates','Sugars','Protein'])

plt.show()

大家可以根据自己对于数据的理解，设置不同的图像样式，来继续发掘数据中的信息。

知识总结

单变量数据:绘制核密度图kdeplot、直方图和核密度图集合distplot。
双变量数据:使用jointplot,设置kind参数可以调整图像的类型。
多变量数据：使用pairplot可以查看两两变量之间的关系。

作业

燃烧我的卡路里

如果你平常喜欢在牛奶、酸奶、冰激凌中肆意地添加一些麦片，那么这个项目很适合你。在这个项目中，我们将会对约80种麦片谷物的营养成分进行分析。

数据集包含以下变量：

• name：麦片名称
• mfr：制造商
• type：种类，热加工或冷加工
• calories：卡路里含量
• protein：蛋白质含量
• fat：脂肪含量
• sodium：钠含量
• fiber: 膳食纤维含量
• carbo: 复合碳水化合物含量
• sugars: 糖含量
• potass: 钾含量
• vitamins: 维生素含量
• shelf: 展示架层数
• weight: 一份的重量
• cups: 一份的杯数
• rating: 麦片评级

# 导入项目使用的模块
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

# TODO
# 读取数据，保存到变量cereal中
# 数据集储存在上一目录 data 文件夹中，eg:../data/cereal.csv'
# 查看数据的前五行
cereal =pd.read_csv('cereal.csv') 
cereal.head()

	name	mfr	type	calories	protein	fat	sodium	fiber	carbo	sugars	potass	vitamins	shelf	weight	cups	rating
0	100% Bran	N	C	70	4	1	130	10.0	5.0	6	280	25	3	1.0	0.33	68.402973
1	100% Natural Bran	Q	C	120	3	5	15	2.0	8.0	8	135	0	3	1.0	1.00	33.983679
2	All-Bran	K	C	70	4	1	260	9.0	7.0	5	320	25	3	1.0	0.33	59.425505
3	All-Bran with Extra Fiber	K	C	50	4	0	140	14.0	8.0	0	330	25	3	1.0	0.50	93.704912
4	Almond Delight	R	C	110	2	2	200	1.0	14.0	8	-1	25	3	1.0	0.75	34.384843

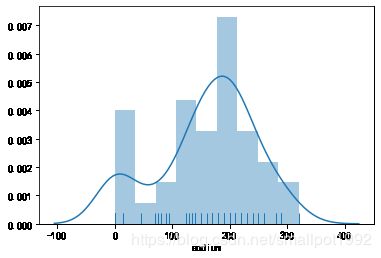
核密度估计图

# TODO
# 绘制钠含量distplot，并且显示边际毛毯
sns.distplot(cereal.sodium,rug=True)
plt.show()

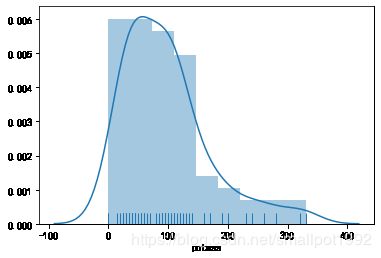
# TODO
# 绘制钾含量distplot，并且显示边际毛毯
sns.distplot(cereal.potass,rug=True)
plt.show()

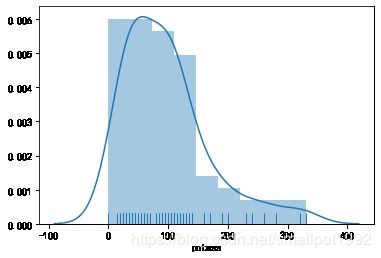
# TODO
# 绘制复合碳水化合物含量distplot，并且显示边际毛毯
sns.distplot(cereal.potass,rug=True)
plt.show()

双变量联合回归图

# TODO
# 绘制卡路里和糖含量联合散点回归图 ，其中，x轴设置为卡路里数据
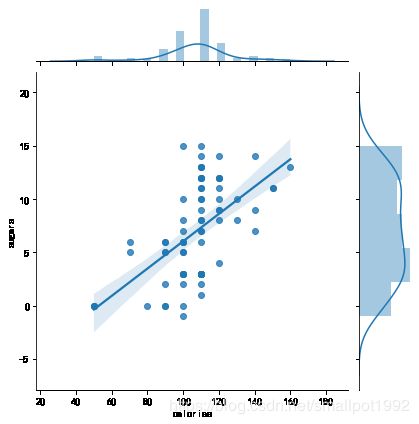
sns.jointplot(x='calories',y='sugars',data=cereal,kind='reg')
plt.show()

# TODO
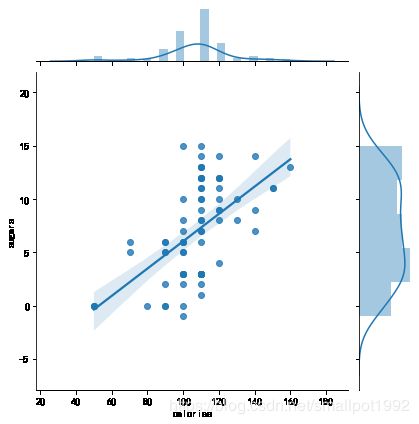
# 绘制卡路里和糖含量联合散点回归图 ，其中，x轴设置为卡路里数据
sns.jointplot(x='calories',y='sugars',data=cereal,kind='reg')
plt.show()

# TODO
# 绘制卡路里和糖含量联合散点回归图 ，其中，x轴设置为卡路里数据
sns.jointplot(x='calories',y='sugars',data=cereal,kind='reg')
plt.show()

多变量关系分布图

# TODO
# 绘制'sugars','potass','calories','rating'关系分布图，并且设置分类为'type'
sns.pairplot(cereal,hue='type',vars=['sugars','potass','calories','rating'])
plt.show()

c:\users\administrator\appdata\local\programs\python\python37\lib\site-packages\seaborn\distributions.py:288: UserWarning: Data must have variance to compute a kernel density estimate.
  warnings.warn(msg, UserWarning)

结婚or离婚

近年来，国内结婚率越来越低，相反离婚率越来越高，在这个项目中我们将对中国各省2009年到2017年的离婚率和结婚率数据进行分析。

# 导入项目使用的模块
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

# TODO
# 读取两个数据集
# 数据集储存在上一目录 data 文件夹中，eg:../data/divorce.csv'、'../data/marriage.csv'
# 分别查看前五行数据
divorce = pd.read_csv('divorce.csv')
marriage = pd.read_csv('marriage.csv')
print(marriage.head())

     area   2017   2016   2015   2014   2013   2012   2011  2010   2009
0     北京市  15.15  16.62  16.60  17.00  16.37  17.41  17.32  13.8  18.18
1     天津市   9.51   9.82  10.12   9.94  10.26  10.14  10.41   8.7  10.40
2     河北省  50.49  55.19  60.94  66.13  74.08  74.53  77.72  75.0  72.00
3     山西省  28.77  30.01  34.68  35.07  38.40  36.28  33.96  36.1  34.36
4  内蒙古自治区  18.70  19.84  21.79  21.68  22.16  20.77  21.53  20.3  18.84

#绘制2009年结婚率核密度图，且设置标题为：'2009年结婚率核密度图'
sns.distplot(marriage['2009'],rug=True)
plt.title('2009年结婚率核密度图')
plt.show()

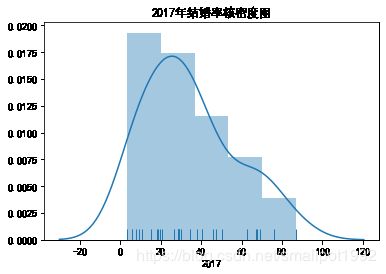
sns.distplot(marriage['2017'],rug=True)
plt.title('2017年结婚率核密度图')
plt.show()

#绘制2009年各地区结婚率、离婚率双变量联合回归图
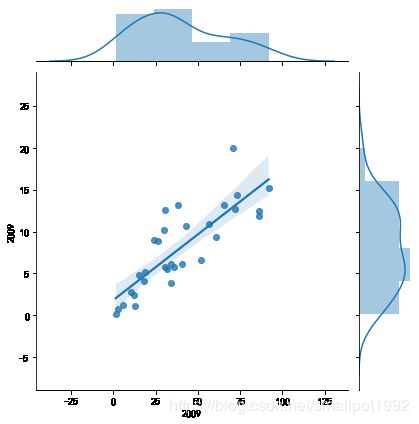
sns.jointplot(x=marriage['2009'],y=divorce['2009'],kind='reg')
plt.show()

#绘制2017年各地区结婚率、离婚率双变量联合回归图
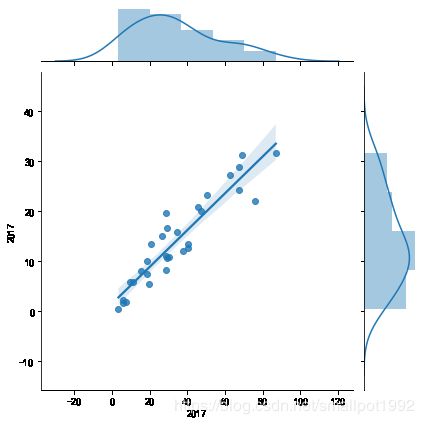
sns.jointplot(x=marriage['2017'],y=divorce['2017'],kind='reg')
plt.show()

各省市结婚率/离婚率折线图

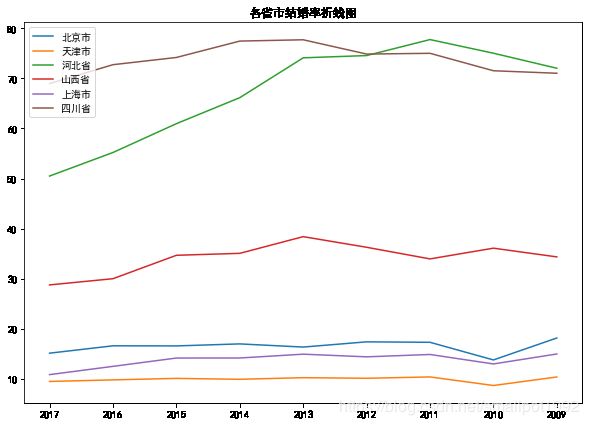
# 使用matplotlib绘制'北京市'、'天津市'、'河北省'、'山西省'、'上海市'、'四川省'结婚率折线图，绘制图例，
#每个折线的图例标签与数据中的area对应字段相同，且设置标题为'各省市结婚率折线图'

plt.figure(figsize=(10,7))
plt.plot(marriage.iloc[0,1:],label='北京市')
plt.plot(marriage.iloc[1,1:],label='天津市')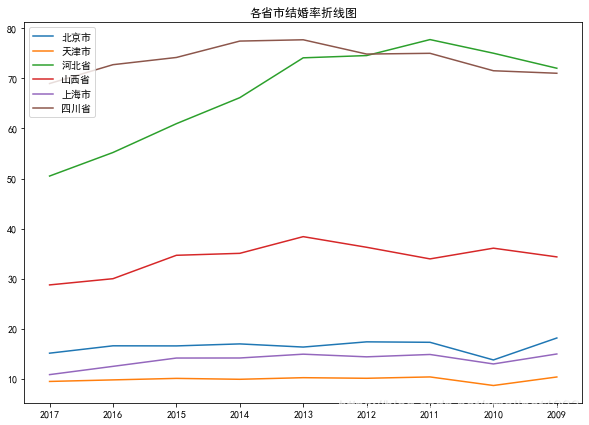![在这里插入图片描述](https://img-blog.csdnimg.cn/20200424104830216.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3NtYWxscG90MTk5Mg==,size_16,color_FFFFFF,t_70#pic_center)

plt.plot(marriage.iloc[2,1:],label='河北省')
plt.plot(marriage.iloc[3,1:],label='山西省')
plt.plot(marriage.iloc[8,1:],label='上海市')
plt.plot(marriage.iloc[22,1:],label='四川省')
plt.legend()
plt.title('各省市结婚率折线图')
plt.show()

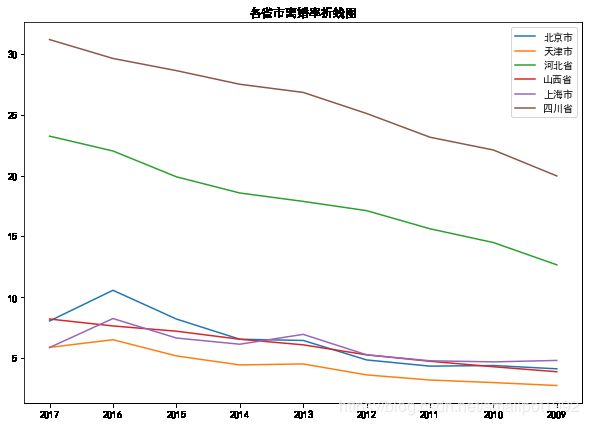
# 使用matplotlib绘制'北京市'、'天津市'、'河北省'、'山西省'、'上海市'、'四川省'离婚率折线图，
#且每个折线的图例标签与数据中的area对应字段相同，设置标题为'各省市离婚率折线图'
plt.figure(figsize = (10,7))
plt.plot(divorce.iloc[0,1:], label = '北京市')
plt.plot(divorce.iloc[1, 1:], label = '天津市')
plt.plot(divorce.iloc[2, 1:], label = '河北省')
plt.plot(divorce.iloc[3, 1:], label = '山西省')
plt.plot(divorce.iloc[8, 1:], label = '上海市')
plt.plot(divorce.iloc[22, 1:], label = '四川省')
plt.legend()
plt.title('各省市离婚率折线图')
plt.show()