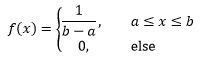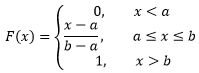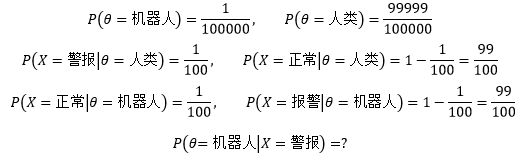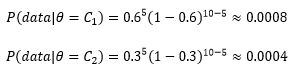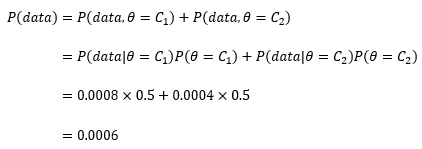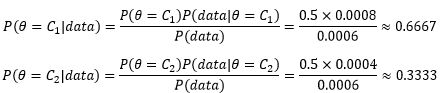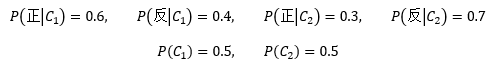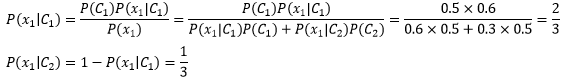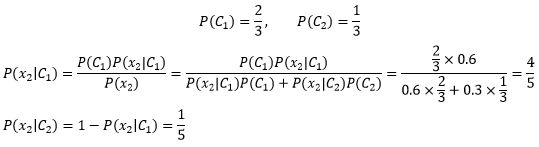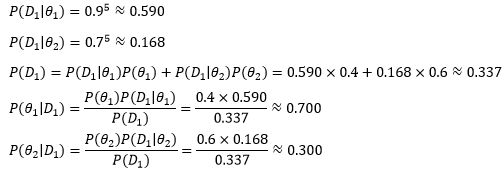概率统计16——均匀分布、先验与后验

 

相关阅读：

最大似然估计(概率10)

重要公式（概率4）

概率统计13——二项分布与多项分布

贝叶斯决策理论（1）基础知识 | 数据来自于一个不完全清楚的过程……

均匀分布

　　简单来说，均匀分布是指事件的结果是等可能的。掷骰子的结果就是一个典型的均匀分布，每次的结果是6个离散型数据，它们的发生是等可能的，都是1/6。均匀分布也包括连续形态，比如一份外卖的配送时间是10~20分钟，如果我点了一份外卖，那么配送员会在接单后的10~20分钟内的任意时间送到，每个时间点送到的概率都是等可能的。

　　很多时候，均匀分布是源于我们对事件的无知，比如面对中途踏上公交车的陌生人，我们会判断他在之后任意一站下车的可能性均相等。正是由于不认识这个人，也不知道他的目的地是哪里，因此只好认为在每一站下车的概率是等可能的。如果上车的是一个孕妇，并且接下来公交车会经过医院，那么她很可能是去医院做检查，她在医院附近下车的概率会远大于其他地方。虽然不认识这名孕妇，但孕妇的属性为我们提供了额外的信息，让我们稍稍变的“有知”，从而打破了分布的均匀性。

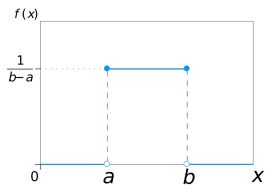
　　根据“均匀”的概念，如果随机变量X在[a, b]区间内服从均匀分布，则它的密度函数是：

　　这里的区间是(a,b)还是[a,b]没什么太大关系。

　　均匀分布记作X~U(a, b)，当a ≤ x ≤ b时，分布函数是：

　　由此可知X~U(a, b)在随机变量是任意取值时的分布函数：

　　假设某个外卖配送员送单的速度在10~15分钟之间，那么这个配送员接单后在13分钟之内送到的概率是多少？

　　我们同样对这名配送员缺乏了解，也不知道他的具体行进路线，因此认为他在10~15分钟之间送到的概率是等可能的，每个时间点送到的概率都是dx/(15-10)，因此在13分钟内送到的概率是：

　　其实也没必要每次都用积分，直接用概率分布的公式就可以了：

先验与后验

　　某个城市有10万人，其中有一个是机器人伪装的。现在有关部门提供了一台检测仪，当检测仪认为被检测对象是机器人时就会发出刺耳的警报。但这台检测仪并不完美，仍有1%的错误率，也就是说有1%的概率把一个正常人判断成机器人，也有1%的概率把机器人误判为正常人。对于全城的任何一个居民来说，如果检测仪将他判断为机器人，那么他真是机器人的概率是多大？

　　我们用随机变量θ表示一个居民的真实身份，X表示检测结果（有警报和正常两种结果），上面的问题可以用以下概率表示：

　　我们根据上面的式子来解释先验概率和后验概率。

　　先验概率（prior probability），是指根据以往经验和分析得到的概率，与试验结果无关。这里的“以往经验”可能是一批历史数据的统计，也可能是主观的预估。值得注意的是，主观预估绝非瞎猜，实际上主观预估也是一种不精确的统计分析。比如我们估计一个外卖配送员的交通工具是电瓶车，虽然是一个主观的猜测，但准确率相当高，毕竟在方圆五公里之内，电瓶车是最灵活快捷的交通工具。上面的P(θ=机器人)是一个先验概率，它是事先知道的，不管有没有检测仪，检测结果怎么样，我们都事先认定这个城市中有一个机器人伪装成人类的概率是10万分之一，至于是怎么知道的就是另外一回事了，可能是接到群众的举报，也可能是有关部门提供的消息。

　　10万人中有一个是机器人伪装的，先验概率是P(θ= 机器人) = 1/100000。是否有可能有另一个先验概率，比如10万人中有1/100是机器人伪装的？当然可以。按照这个逻辑，先验概率可以是0~1之间的任何数值。

　　这里的参数θ代表居民的身份，有两个取值，机器人和人类，P(θ)表示θ是某个取值的概率，既然是概率，那么θ也必然服从某个分布，这个分布就称为先验分布。

　　简单而言，先验概率是对随机变量θ的取值的预估，先验分布是关于先验概率的概率分布（即P(θ)中θ取值的分布）。如果θ的取值是连续型的，它的先验分布就是连续型分布。

 

　　后验概率（posterior probability），是在相关结果或者背景给定并纳入考虑之后的条件概率。比如一个熊孩子持续三分钟没有动静，以此为前提，这个熊孩子在“干大事”的概率就是一个后验分布，表示为P(干大事|三分钟没动静)。对P(θ=机器人|X=警报)来说，检测结果已经有了，是X=警报，在此基础上求接受检测的居民是否真是机器人的概率，因此这是一个后验概率。

　　

　　似然函数（likelihood function）用来描述已知随机变量输出结果时，未知参数的可能取值。关于似然的概念前面已经详细介绍过，可参考 最大似然估计(概率10)。

　　

　　最后看看问题的答案。贝叶斯公式告诉我们：

校正先验

　　假设有两枚硬币C1和C2，它们投出正面的概率分别是0.6和0.3。现在取其中一枚连投10次，得到的结果是前5次正面朝上，后5次反面朝上，试验中选择的最可能是哪枚硬币？

　　

　　我们把参数θ看成硬币的选择，只有两枚硬币，也许在现实中它们长的不一样，大多数人会选择更漂亮的C1，但是在题目中，实验前我们对两枚硬币都缺乏了解，基于“无知”的原则，认为选择C1和C2的概率是等可能的，即P(θ=C1)= P(θ=C2)=0.5。有了先验概率后，可以代入贝叶斯公式计算后验概率：

　　这里data是10次投硬币的结果，无论选择那枚硬币，投掷的结果都符合伯努利分布：

　　P(data)则需要借助全概率公式：

　　现在可以分别计算实验前选择C1硬币或C2硬币的概率：

　　这个数字符合直觉。对于分类来说，在比较C1和C2的后验概率时，二者的分母都是P(data)，也就是说P(data)并没有起到实际作用，因此对于分类器来说无需计算P(data)：

　　

　　贝叶斯公式告诉我们，先验概率是在实验前对原因的预估，后验概率是在试验后根据结果反推原因，或者说是根据结果对最初预估的修正。既然如此，一次修正得到的并不一定是最佳结果，可以尝试多次修正，前一个样本点的后验会被下一次估计当作先验。我们根据这种思路重新计算一下C1的后验概率。

　　一共抛了10次硬币，用{x1, x2, …, x10}代表每次抛硬币的结果，x1~x5是正面，x6~x10是反面，仍然在实验前认为选择C1和C2的概率是等可能的，下面是已知信息：

　　与之前不同，这次我们每次只看一枚硬币，以此来计算θ的后验概率：

　　后验信息代表一次历史经验，比试验前的“无知”稍强一些。接下来，我们用后验概率作为下一次迭代的先验概率：

　　继续迭代，直到x10为止，将最终得到的先验概率就是最终结果。

p_1_c1, p_0_c1 = 0.6, 0.4  # P(1|c1) = 0.6, P(0|c1) = 0.4, 1和0分别代表正反
p_1_c2, p_0_c2 = 0.3, 0.7  # P(1|c2) = 0.3, P(0|c2) = 0.7


def posterior_theta(p_c1, p_c2, x):
    '''
    计算θ的后验概率
    :param p_c1: c1的先验概率P(C1)
    :param p_c2: c2的先验概率P(C2)
    :param x: 硬币的结果
    :return: 后验概率P(C1|x)和P(C2|x)
    '''
    p_x_c1 = p_1_c1 if x == 1 else p_0_c1
    p_x_c2 = p_1_c2 if x == 1 else p_0_c2
    # 计算后验概率P(C1|x)
    p_c1_x = p_c1 * p_x_c1 / (p_x_c1 * p_c1 + p_x_c2 * p_c2)
    p_c2_x = 1 - p_c1_x
    return p_c1_x, p_c2_x


data = [1, 1, 1, 1, 1, 0, 0, 0, 0, 0]  # 5正5反
p_c1, p_c2 = 0.5, 0.5  # 初始先验P(C1) = P(C2) = 0.5
for x in data:
    # 用后验作为下一个样本点的先验
    p_c1, p_c2 = posterior_theta(p_c1, p_c2, x)
    print('P(C1)={0}, P(C2)={1}'.format(p_c1, p_c2))

　　P(C1)=0.6666666666666667, P(C2)=0.33333333333333326

　　P(C1)=0.8, P(C2)=0.19999999999999996

　　P(C1)=0.888888888888889, P(C2)=0.11111111111111105

　　P(C1)=0.9411764705882353, P(C2)=0.05882352941176472

　　P(C1)=0.9696969696969696, P(C2)=0.030303030303030387

　　P(C1)=0.948148148148148, P(C2)=0.05185185185185204

　　P(C1)=0.9126559714795006, P(C2)=0.08734402852049938

　　P(C1)=0.8565453785027182, P(C2)=0.14345462149728183

　　P(C1)=0.7733408854904177, P(C2)=0.22665911450958232

　　P(C1)=0.6609783156833076, P(C2)=0.33902168431669244

　　上面的迭代过程是一个将样本点逐步增加到学习器的过程，前一个样本点的后验会被下一次估计当作先验。可以说，贝叶斯学习是在逐步地更新先验，逐步通过新样本对原有的分布进行修正。

　　

　　在实际应用中当然不会每次仅仅增加一个样本点。下面的例子更好地说明了这个逐步更新先验的过程。

　　为了提高产品的质量，公司经理考虑增加投资来改进生产设备，预计投资90万元，但从投资效果来看，两个顾问给出了不同的预言：

　　θ1顾问：改进生产设备后，高质量产品可占90%

　　θ2顾问：改进生产设备后，高质量产品可占70%

　　根据经理的以往经验，两个顾问的靠谱率是P(θ1)=0.4, P(θ2)=0.6。这两个概率是先验概率，是经理的主观判断。似乎θ2更靠谱一些，但是这次，θ2顾问意见太保守了，为了得到更准确的信息，经理进行了小规模的试验，结果第一批制作的5个产品全是令人兴奋的高质量产品。

　　用D1表示本次实验的5个产品，可以得到下面的结论：

　　在第一次试验后，经理针对本次实验对两个顾问的靠谱率做出了修正，认为P(θ1)=0.700, P(θ2)=0.300，这个概率更符合本次实验的结果，或者说试验结果改变了经理的主观看法。

　　当然5个产品说明不了太大问题，于是经理又试制了10个产品（用D2表示），结果有9个是高质量的，根据这个结果继续对顾问的靠谱率进行修正：

　　两个顾问的靠谱率在D2中再次得到修正。

　　

---

　　出处：微信公众号 "我是8位的"

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！ 

　　扫描二维码关注作者公众号“我是8位的”