线性模型 最小二乘法参数估计 批量梯度下降法

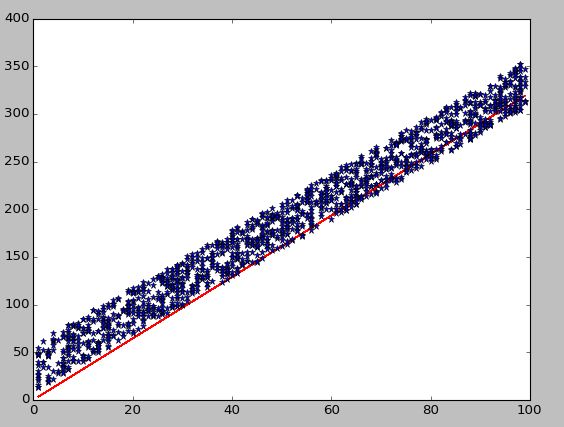
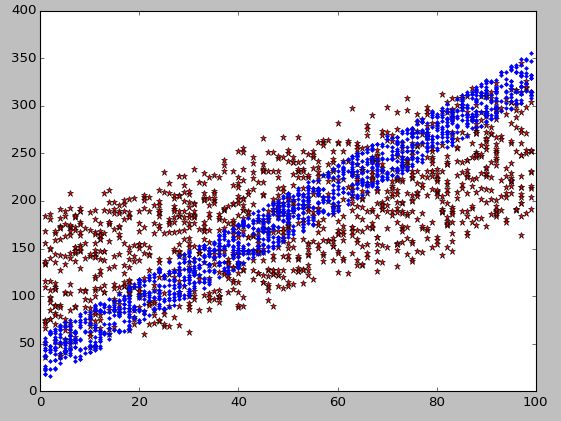
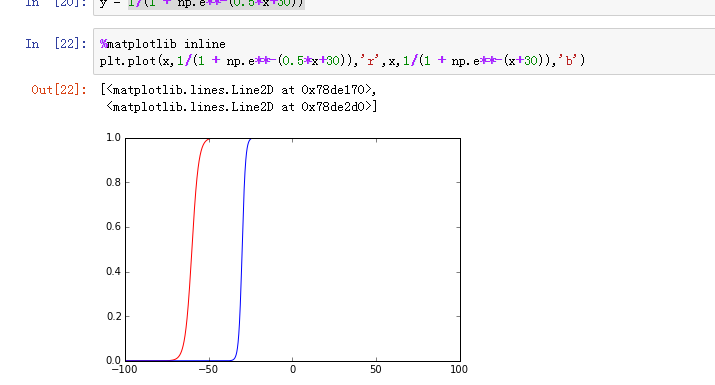
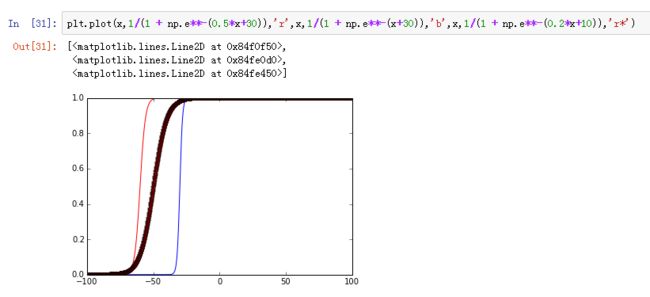
均值滤波：红色为原始带有噪声的数据，蓝色为滤波后的数据

---

# coding:utf-8

fromsklearn.datasetsimportfetch_20newsgroups

fromsklearn.datasetsimportfetch_california_housing

categories = ['comp.graphics',

'comp.os.ms-windows.misc',

'comp.sys.ibm.pc.hardware',

'comp.sys.mac.hardware',

'comp.windows.x'];

newsgroup_train = fetch_20newsgroups(subset='train',categories= categories);

house_price_train = fetch_california_housing()

print'down'

importnumpyasnp

importmatplotlib.pyplotasplt

importpandasaspd

##

#自制数据y = x1+2*x2 + 3 * x3

##

FEATURE_NUM =1

w = np.arange(3,4).reshape(FEATURE_NUM,-1)

x = np.random.randint(1,100,size= (1300,FEATURE_NUM))

y = x.dot(w)  +9+ np.random.randint(1,50,(1300,1))

plt.plot(x,y,'*')

plt.show()

house_price_train.data = x

house_price_train.target = y

train_x = house_price_train.data[:1000]

train_y = np.array( house_price_train.target[:1000]).reshape(1000,-1)

test_x = house_price_train.data[100:]

test_y = np.array(house_price_train.target[100:])

# linear regression

feature_num  =len(train_x[0])

train_sample_num =len(train_x)

test_sample_num =len(test_x)

train_x = np.concatenate((train_x,np.ones((train_sample_num,1))),axis=1)

test_x = np.concatenate((test_x,np.ones((test_sample_num,1))),axis=1)

# #步骤：

# 1.定义model输入theta x给出f(x)

# 2.计算误差

# 3.梯度下降求解

#后面可以用ufunc求解f = fromfunc(func,n_in,n_dout)    f(ndarray)

defmodel(theta,x):

returnnp.sum(theta*x)

defcost(theta,x,y):

returny - model(theta,x)

w = np.zeros(feature_num +1)

deftrain(train_x,train_y):

globalw

theta = np.zeros((feature_num+1,1))

last_theta =np.zeros((feature_num+1,1))

eps=0.001

_cost=999

COUNT =10000

idx=0

change =999

whilechange >0.001andidx < COUNT:

total_cost = train_x.dot(theta)

_cost= np.linalg.norm(total_cost - train_y)

theta = theta -0.000001* (1.0/train_sample_num)* (train_x.T).dot((total_cost - train_y))

# theta = theta + 0.00000001 *(train_x.T).dot((train_y - total_cost ))

change = np.linalg.norm(theta - last_theta)

last_theta = theta

idx +=1

# print idx,change,_cost

printidx,change,theta.tolist()

ly = train_x.dot(theta)

plt.plot(train_x[::,0].reshape(train_sample_num,),ly.reshape(train_sample_num,),'r',x,y,'b*')

plt.show()

print"theta:",theta

returntheta

defpredict(x,theta):

returnmodel(theta,x)

if__name__ =="__main__":

theta = train(train_x,train_y)

print"done"

# least double multiply