《数据结构与算法Python语言描述》裘宗燕 笔记 第四章 字符串

 

《数据结构与算法Python语言描述》裘宗燕 笔记系列
该系列笔记结合PPT的内容整理的，方便以后复习，有需要的朋友可以看一下。

源码重新整理了

 

地址：https://github.com/StarsAaron/DS/tree/master

 

字符串的相关概念

- Python 字符串（回顾）

- 字符串匹配和算法

- 进一步的模式匹配问题

- 正则表达式

- Python 的正则表达式

- 应用举例

 

字符串（简称串）是特殊的线性表

 

字符串表示的两个问题：

（1）串内容存储。两个极端：

- 连续存储在一块存储区；

- 一个字符存入一个独立存储块，链接起来。也可以采用某种中间方式，把串中字符分段保存在一组存储块里，链接起这些存储块

（2）串结束的表示，不同字符串长度可能不同，必须表示串到哪里结束。

 

两种基本方式：

-用专门数据域记录字符串长度；

-用一个特殊符号表示串结束（例如 C 语言的字符串采用这种方式）

Python 内部类型 str 是抽象字符串概念的一个实现

（1）str 是不变类型， str 对象创建后的内容（和长度）不变

（2）但不同的 str 对象长度不同，需要记录

 

Python 采用一体式的连续形式表示 str 对象，见下图

 

字符串匹配

朴素匹配算法：

朴素匹配算法简单，易理解，但效率低。造成效率的主要操作是执行中可能出现的回溯：遇字符不等时将模式串 p 右移一个字符，再次从 p0（重置 j = 0 后）开始比较

 

最坏情况是每趟比较都在最后出现不等，最多比较 n－m＋1 趟，总比较次数为 m*(n－m＋1)，所以算法时间复杂性为 O(m*n)

/**
 * 暴力破解法
 * @param ts 主串
 * @param ps 模式串
 * @return 如果找到，返回在主串中第一个字符出现的下标，否则为-1
 */
public static int bf(String ts, String ps) {
    char[] t = ts.toCharArray();
    char[] p = ps.toCharArray();
    int i = 0; // 主串的位置
    int j = 0; // 模式串的位置
    while (i < t.length && j < p.length) {
       if (t[i] == p[j]) { // 当两个字符相同，就比较下一个
           i++;
           j++;
       } else {
           i = i - j + 1; // 一旦不匹配，i后退
           j = 0; // j归0
       }
    }
    if (j == p.length) {
       return i - j;
    } else {
       return -1;
    }
}

 

KMP算法

KMP 算法的基本想法：在匹配失败时，利用已做匹配中得到的信息，把模式串尽可能前移。匹配中只做不得不做的字符比较，不回溯

 

什么是KMP算法：

KMP是三位大牛：D.E.Knuth、J.H.Morris和V.R.Pratt同时发现的。

KMP算法要解决的问题就是在字符串（也叫主串）中的模式（pattern）定位问题。通过减少回溯的次数来降低算法的复杂度。

 

朴素匹配算法是没有问题的，但不够好！

 

“利用已经部分匹配这个有效信息，保持i指针不回溯，通过修改j指针，让模式串尽量地移动到有效的位置。”

 

整个KMP的重点就在于当某一个字符与主串不匹配时，我们应该知道j指针要移动到哪？

 

接下来我们自己来发现j的移动规律：

 

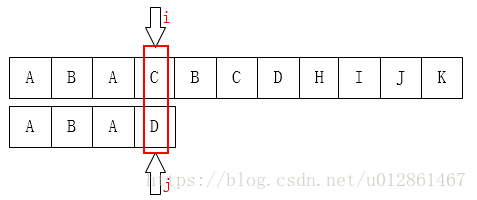
如图：C和D不匹配了，我们要把j移动到哪？显然是第1位。为什么？因为前面有一个A相同啊：

 

如下图也是一样的情况：

 

可以把j指针移动到第2位，因为前面有两个字母是一样的：

 

当匹配失败时，j要移动的下一个位置k。存在着这样的性质：最前面的k个字符和j之前的最后k个字符是一样的。

如果用数学公式来表示是这样的

P[0 ~ k-1] == P[j-k ~ j-1]

 

弄明白了这个就应该可能明白为什么可以直接将j移动到k位置了。

因为:

当T[i] != P[j]时

有T[i-j ~ i-1] == P[0 ~ j-1]

由P[0 ~ k-1] == P[j-k ~ j-1]

必然：T[i-k ~ i-1] == P[0 ~ k-1]

这一段只是为了证明我们为什么可以直接将j移动到k而无须再比较前面的k个字符。

好，接下来就是重点了，怎么求这个（这些）k呢？因为在P的每一个位置都可能发生不匹配，也就是说我们要计算每一个位置j对应的k，所以用一个数组next来保存，next[j] = k，表示当T[i] != P[j]时，j指针的下一个位置。

 

这个next数组保存的就是部分匹配值，记录的就是最长相同前缀和后缀的长度。

以"ABCDABD"为例，

－　"A"的前缀和后缀都为空集，共有元素的长度为0；

－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

 

这里是整个算法最关键的地方

 

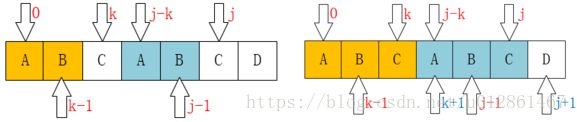
现在考虑 pnext 表的构造，以下面情况为例

新位置的前缀子串应该与匹配失败字符之前同长度的子串相同

如果在模式串匹配失败时，前面一段里满足上述条件的位置不止一处，只能移到最近的那个位置（保证不遗漏可能的匹配）

 

已知 ki 值只依赖于 p 本身的前i个字符

 

模式串的正确前移位置移位，必须保证其前缀 p0 …pk-1与 t 中对应那些字符匹配，而这实际上也就是与pi-k …pi-1匹配

正确 k 值由 p 前 i 个字符形成的子串里相等的前缀和后缀决定取这种前后缀中最长的（前移最短），就能保证不忽略可能的匹配

 

如果 p0…pi-1 最长相等前后缀（不包括 p0…pi-1 本身但可为空）的长度为 k (0 ≤ k < i-1)。当 pi ≠ tj 时 p 应右移 i - k 位，随后比较 pk 与 tj 也就是说，应该把 pnext[i] 设置为 k

 

求 pnext 的问题变成对每个 i 求 p 的（前缀）子串 p0…pi-1 的最长相等前后缀的长度。 KMP 提出了一种巧妙的递推算法

 

针对 i 递推计算最长相等前后缀的长度。设对 i-1 已经算出，于是

 

- 如果 pi = pk， pnext[i] 应该为 k，继续

- 否则把 p0...pk-1的最长相同前缀移过来继续检查

 

利用已知 pnext[0]= -1 直至 pnext[i] 求 pnext[i+1] 的算法：

1. 假设 next [i] = k。若pk = pi，则 p0… pi-k…pi 的最大相同前后缀的长度就是 k+1，记入 pnext[i+1]，将 i 值加一后继续递推（循环）

2. 若pk ≠ pi 设 k 为 pnext[k] 的值（设 k 为 pnext[k]，也就是去考虑前一个更短的保证匹配的前缀，从那里继续检查）

3. 若 k 值为 -1（一定来自 pnext），得到 p0… pi-k…pi 中最大相同前后缀的长度为 0，设 pnext [i+1] = 0，将 i 值加一后继续递推

public static int[] getNext(String ps) {
    char[] p = ps.toCharArray();
    int[] next = new int[p.length];
    next[0] = -1;
    int j = 0;
    int k = -1;
    while (j < p.length - 1) {
       if (k == -1 || p[j] == p[k]) {
           next[++j] = ++k;
       } else {
           k = next[k]; // 如果p[j]和p[k] 不相等，k取下一个位置
       }
    }
    return next;
}

next[j]的值（也就是k）表示，当P[j] != T[i]时，j指针的下一步移动位置。

先来看第一个：当j为0时，如果这时候不匹配，怎么办？

 

像上图这种情况，j已经在最左边了，不可能再移动了，这时候要应该是i指针后移。所以在代码中才会有next[0] = -1;这个初始化。

如果是当j为1的时候呢？

 

显然，j指针一定是后移到0位置的。因为它前面也就只有这一个位置了~~~

 

下面这个是最重要的，请看如下图：

 

 

请仔细对比这两个图。

我们发现一个规律：

当P[k] == P[j]时，

有next[j+1] == next[j] + 1

其实这个是可以证明的：

因为在P[j]之前已经有P[0 ~ k-1] == p[j-k ~ j-1]。（next[j] == k）

这时候现有P[k] == P[j]，我们是不是可以得到P[0 ~ k-1] + P[k] == p[j-k ~ j-1] + P[j]。

即：P[0 ~ k] == P[j-k ~ j]，即next[j+1] == k + 1 == next[j] + 1。

这里的公式不是很好懂，还是看图会容易理解些。

 

那如果P[k] != P[j]呢？比如下图所示：

像这种情况，如果你从代码上看应该是这一句：k = next[k];为什么是这样子？你看下面应该就明白了。

 

 

现在你应该知道为什么要k = next[k]了吧！像上边的例子，我们已经不可能找到[ A，B，A，B ]这个最长的后缀串了，但我们还是可能找到[ A，B ]、[ B ]这样的前缀串的。所以这个过程像不像在定位[ A，B，A，C ]这个串，当C和主串不一样了（也就是k位置不一样了），那当然是把指针移动到next[k]啦。

 

有了next数组之后就一切好办了，我们可以动手写KMP算法了：

 

public static int KMP(String ts, String ps) {
    char[] t = ts.toCharArray();
    char[] p = ps.toCharArray();
    int i = 0; // 主串的位置
    int j = 0; // 模式串的位置
    int[] next = getNext(ps);
    while (i < t.length && j < p.length) {
       if (j == -1 || t[i] == p[j]) { // 当j为-1时，要移动的是i，当然j也要归0
           i++;
           j++;
       } else {
           // i不需要回溯了
           // i = i - j + 1;
           j = next[j]; // j回到指定位置
       }
    }
    if (j == p.length) {
       return i - j;
    } else {
       return -1;
    }
}

和暴力破解相比，就改动了4个地方。其中最主要的一点就是，i不需要回溯了。

 

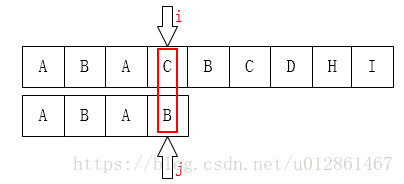
最后，来看一下上边的算法存在的缺陷。来看第一个例子：

 

显然，当我们上边的算法得到的next数组应该是[ -1，0，0，1 ]

所以下一步我们应该是把j移动到第1个元素咯：

 

不难发现，这一步是完全没有意义的。因为后面的B已经不匹配了，那前面的B也一定是不匹配的，同样的情况其实还发生在第2个元素A上。

显然，发生问题的原因在于P[j] == P[next[j]]。

所以我们也只需要添加一个判断条件即可：

 

public static int[] getNext(String ps) {
    char[] p = ps.toCharArray();
    int[] next = new int[p.length];
    next[0] = -1;
    int j = 0;
    int k = -1;
    while (j < p.length - 1) {
       if (k == -1 || p[j] == p[k]) {
           if (p[++j] == p[++k]) { // 当两个字符相等时要跳过
              next[j] = next[k];
           } else {
              next[j] = k;
           }
       } else {
           k = next[k];
       }
    }
    return next;
} 

参考来源： http://www.cnblogs.com/yjiyjige/p/3263858.html

 

算法复杂性

主要因素是循环

while i < m-1: # generate pnext[i+1]

while k >= 0 and p[i] != p[k]:

k = pnext[k]

i, k = i+1, k+1

 

与 KMP 主算法的分析类似（两个算法的循环形式可以相互改变）：

- i 值递增，但不超过 p 的长度 m，说明大循环体执行 m 次

- i 加一时 k 也加一，说明 k 值加一 m 次

- 内层循环执行总导致 k 值减小，但不会小于 –1

上面情况说明循环体的执行次数为 O(m)，算法复杂性也是 O(m)

 

KMP 算法包括 pnext 表构造和实际匹配， O(m+n)。通常情况 m << n，

因此可认为算法复杂性为 O(n)。显然优于 O(m*n)

 

KMP 算法的一个重要优点是执行中不回溯。在处理从外部（外存/网络等）获取的文本时这种特性特别有价值，因为可以一边读一边匹配，不回头重读就不需要保存被匹配串

 

KMP 算法的优势

- KMP 算法特别适合需要多次使用一个模式串的情况和存在许多匹配的情况（如在大文件里反复找一个单词）

- 相应 pnext 表只需建立一次。这种情况下可以考虑定义一个模式类型，将 pnext 表作为模式的一个成分

 

Python 正则表达式

Python 的正则表达式功能由标准包 re 提供。正则表达式可以帮助我们实现一些复杂的字符串操作。正确使用这个包

 

原始字符串

原始字符串（ raw string）是 Python 里一种写字符串文字量的形式，其值（和普通文字量一样）就是 str 类型的对象

原始字符串的形式是在普通字符串文字量前加 r 或 R 前缀，如

R"abcdefg" 

r"C:\courses\pathon\progs"

 

原始字符串里的 \ 不作为换意符，在相应 str 对象里原样保留，除了位于单/双引号前的反斜线符号

 

引入原始字符串机制，只是为了使一些字符串的写法简单

r"C:\courses\pathon\progs" 的等价写法是：

"C:\\courses\\pathon\\progs"

 

生成正则表达式对象： re.compile( pattern, flag = 0)

检索： re.search( pattern, string, flag = 0)

匹配： re.match( pattern, string, flag=0)

分割： re.split( pattern, string, maxsplit=0, flags=0)

找到所有匹配串： re.findall( pattern, string, flags=0 )

 

字符组

字符组表达式 [...] 匹配括号中列出的任一个字符

[abc] 可以匹配字符 a 或 b 或 c

区间形式 [0-9] 是顺序列出的缩写，匹配所有十进制数字字符

[0-9a-zA-Z] 匹配所有字母（英文字母）和数字

 

[^...] 中的 ^ 表示求补，这种模式匹配所有未在括号里列出的字符

[^0-9] 匹配所有非十进制数字的字符

[^ \t\v\n\f\r] 匹配所有非空白字符（非空格/制表符/换行符）

 

如果需要在字符组里包括 ^，就不能放在第一个位置，或者写 \^；如果需要在字符组包括 - ]，也必须写 \- 或 \]

 

圆点字符 . 匹配任意一个字符

a..b 匹配所有以 a 开头 b 结束的四字符串

a[1-9][0-9] 匹配 a10, a11, ..., a99

 

常用字符组

为了方便， re 用换意串形式定义了几个常用字符组，包括：

\d：与十进制数字匹配，等价于 [0-9]

\D：与非十进制数字的所有字符匹配，等价于 [^0-9]

\s：与所有空白字符匹配，等价于 [ \t\v\n\f\r]

\S：与所有非空白字符匹配，等价于 [^ \t\v\n\f\r]

\w：与所有字母数字字符匹配，等价于 [0-9a-zA-Z]

\W：与所有非字母数字字符匹配，等价于 [^0-9a-zA-Z]

 

重复

*：0 次或任意多次出现匹配

+：表示 1 次或多次重复

?：表示 0 次或 1 次重复

确定次数的重复用 {n} 表示， α{n} 与 α 匹配的串的 n 次重复匹配

重复范围用 {m,n} 表示

 

* + ? {m,n} 都采取贪婪匹配策略，与被匹配串中最长的合适子串匹配（因为它们可能出现更大的模式里，要照顾上下文的需要）

 

*? +? ?? {m,n}?（各运算符后增加一个问号）采用非贪婪匹配（最小匹配）的策略

 

 

选择

选择运算符 | 描述两种或多种情况之一的匹配。如果 α 或者 β 与一个串匹配，那么 α|β 就与之匹配

 

首尾匹配

- 行首匹配：以 ^ 符号开头的模式，只能与一行的前缀子串匹配

re.search('^for', 'books for children') 得到 None

- 行尾匹配：以 $ 符号结尾的模式，只与一行的后缀匹配

re.search('fish$', 'cats like to eat fishes') 得到 None

 

re.fullmatch( pattern, string, flags=0)

如果整个 string 与 pattern 匹配则成功并返回相应的 match 对象，否则返回 None

 

re.finditer( pattern, string, flags=0)

功能与 findall 类似，但返回的不是表而是一个迭代器，使用该迭代器可顺序取得表示各非重叠匹配的 match 对象

 

re.sub( pattern, repl, string, count=0, flags=0)

做替换，把 string 里顺序与 pattern 匹配的各非重叠子串用 repl 代换。 repl 是串则直接代换；另一情况， repl 还可以是以 match 对象为参数的函数，这时用函数的返回值代换被匹配子串

例：把串 text（例如 Python 程序）里的 \t 都代换为 4 个空格

re.sub('\t', ' ', text)

 

匹配对象（ match 对象）

许多匹配函数在匹配成功时返回一个 match 对象，对象里记录了所完成匹配的有关信息，可以取出使用。下面介绍这方面的情况

 

首先，这样的匹配结果可以用于逻辑判断，成功时得到的 match 对象总表示逻辑真，不成功得到的 None 表示假。例如

match1 = re.search( pt, text)

if match1:

... match1 ... text ... # 使用 match 对象的处理操作