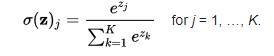如何选择正确的激活函数?
https://baijiahao.baidu.com/s?id=1582399059360085084&wfr=spider&for=pc
激活函数如此重要,那么都有哪些比较热门呢?它们是如何工作的?又适合解决什么问题?本文将为你一一解答。以下是本文目录。
1.简单介绍神经网络
2.什么是激活函数?
3.可以不用激活函数吗?
4.常用的激活函数类型以及使用方法
Binary Step函数
线性函数
Sigmoid函数
tanh函数
ReLU函数
Leaky ReLU函数
Softmax函数
5.如何选择正确的激活函数?
简单介绍神经网络
在深入了解激活函数的细节之前,让我们先回顾一下什么是神经网络,以及它是如何运行的。神经网络是一种非常强大的机器学习机制,它基本上模拟人脑的学习方式。
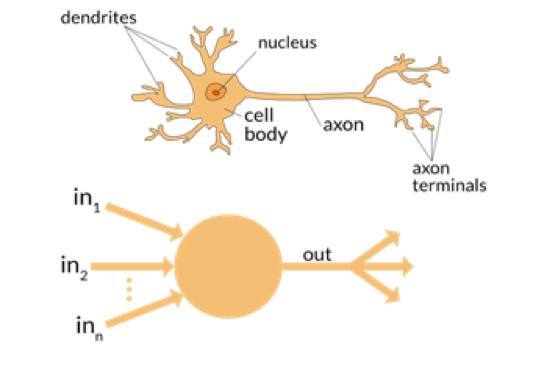
大脑接受外界的刺激,对输入进行加工,然后产生输出。当任务变得复杂时,多个神经元会形成一个复杂的网络,传递信息。
人工神经网络试图模仿类似的行为。下图所示的网络就是由相互连接的神经元组成的人工神经网络。
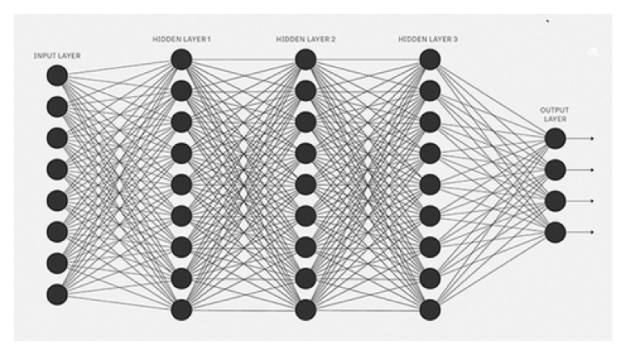
上图中的黑色圆圈代表神经元。 每个神经元都有权重、偏差和激活函数。 信息进入输入层,神经元通过权重和偏差对输入信息进行线性变换,而非线性变换由激活函数完成。 信息从输入层传输到隐藏层,隐藏层对信息进行处理并将结果发送到输出层。 这被称为前向传播。如果产生的输出偏离预期值呢? 在神经网络中,我们将根据误差更新神经元的权重和偏差。 这个过程被称为反向传播。 一旦所有训练数据经过了这一过程,则最终的权重和偏差就被用于测试。
什么是激活函数?
激活函数是人工神经网络的一个极其重要的特征。它决定一个神经元是否应该被激活,激活代表神经元接收的信息与给定的信息有关。
激活函数对输入信息进行非线性变换。 然后将变换后的输出信息作为输入信息传给下一层神经元。
可以不用激活函数吗?
如果激活函数增加了许多复杂性,我们可以不用激活函数吗?
当然不行!当我们不用激活函数时,权重和偏差只会进行线性变换。线性方程很简单,但解决复杂问题的能力有限。没有激活函数的神经网络实质上只是一个线性回归模型。激活函数对输入进行非线性变换,使其能够学习和执行更复杂的任务。我们希望我们的神经网络能够处理复杂任务,如语言翻译和图像分类等。线性变换永远无法执行这样的任务。
激活函数使反向传播成为可能,因为激活函数的误差梯度可以用来调整权重和偏差。如果没有可微的非线性函数,这就不可能实现。
常用的激活函数类型以及使用方法
Binary Step函数
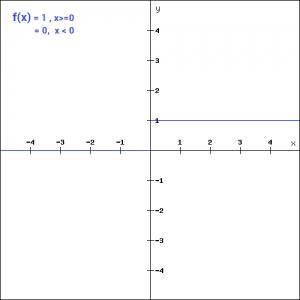
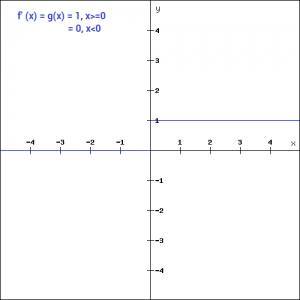
当我们有一个激活函数时,首先联想到的是一个自带阈值的分类器,用于激活神经元。下图中,如果y值高于给定的阈值,则激活神经元,否则禁用。
f(x) = 1, x>=0
Binary Step函数非常简单,可以在创建二进制分类器时使用它。当我们只需要对单个类说“是”或“不是”时,Step函数是最好的选择,因为它要么激活神经元要么把它设为零。
函数的理论性比实用性强,在大多数情况下,我们需要将数据分入多个类而不仅仅放在一类中。此时,Step函数就有点不好用了。
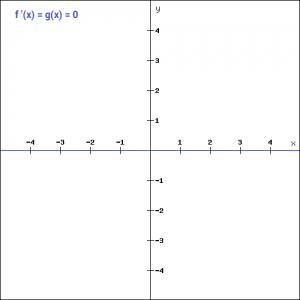
此外,step函数的梯度为零,这使得step函数不能用于反向传播过程中。
f '(x) = 0, for all x
线性函数
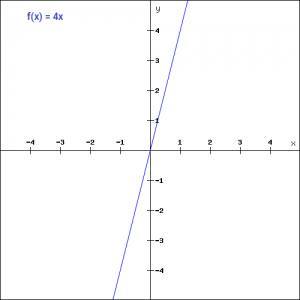
我们看到了step函数的问题,梯度为零,在反向传播过程中不可能更新权重和偏差。此时,我们可以用线性函数来代替简单的step函数。函数表达式:
f(x)=ax
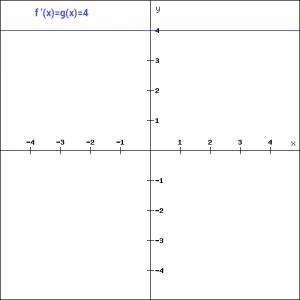
上图中假设a为4。这时激活与输入成正比,输入的x值将被转换为ax。线性函数可用于不同的神经元,也可以激活多个神经元。当我们有多个类时,可以选择f(x)值最大的类。但线性函数仍然存在一个问题。让我们看看这个函数的导数。
f'(x) = a
线性函数的导数是常数,也就是说它不依赖于输入值x
这意味着每次我们做反向传播时,梯度都是一样的。这是一个大问题,我们并没有真正减少误差。不仅如此,假设我们正在做一项复杂任务,需要使用多层神经网络。然而如果每一层都使用线性变换,不管我们有多少层,最终输出的还是输入的线性变换。因此,线性函数只适用于容易解释的简单任务。
Sigmoid函数
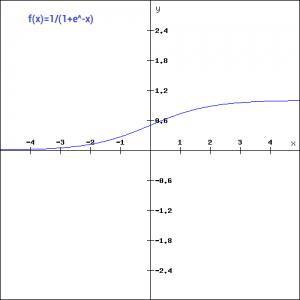
Sigmoid函数曾被广泛应用,但由于其自身的一些缺陷,现在已经很少用了。Sigmoid函数定义如下:
f(x)=1/(1+e^-x)
让我们来看看这个函数。
这是一个平滑函数,并且具有连续性和可微性。与线性函数相比,它的最大优点就是非线性。这意味着多个神经元使用S(Sigmoid简称)形函数作为激活函数时,输出也是非线性的。我们来看看曲线的形状。Y轴范围0-1,x轴在-3到3之间的梯度非常高,但在其他区域形状很平坦。这有什么用吗?
这意味着在[-3,3]这个范围内,x的少量变化也将导致y值的大幅度变化。因此,函数本质上试图将y值推向极值。 当我们尝试将值分类到特定的类时,使用Sigmoid函数非常理想。
让我们来看一下Sigmoid函数的梯度。
它是平滑的,依赖于x值,这意味着在反向传播过程中,我们可以使用这个函数。误差可以被反向传播,权重也可以相应地更新。
即使在今天,sigmoid函数也被广泛使用,但我们仍然需要解决一些问题。正如之前所看到的,这个函数在[-3,3]之外是相当平坦的。这意味着一旦x值不在[-3,3]内,梯度就变得很小,接近于零,而网络就得不到真正的学习。
sigmoid函数的另一个问题是,y轴取值范围[0,1]。这个函数在原点周围不对称,得到的值都是正的。我们不希望下一个神经元得到的值在任何时候都是正值,不过可以通过缩放sigmoid函数来解决这个问题,而这需要在tanh函数中发生。
tanh函数
tanh函数与Sigmoid函数非常相似。它实际上只是Sigmoid函数的一个放大版本。
tanh(x)=2sigmoid(2x)-1
还可以直接表示为:
tanh(x)=2/(1+e^(-2x)) -1
Tanh函数与sigmoid函数相似,但原点对称。它的范围从- 1到1。
它基本上解决了所有值符号相同的问题,而其他属性都与sigmoid函数相同。函数具有连续性和可微性。你可以看到函数是非线性的,所以我们可以很容易地将误差进行反向传播。
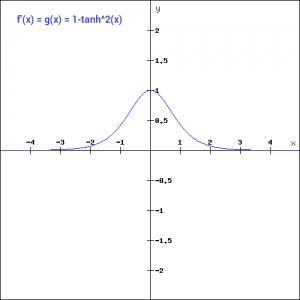
让我们看一下tanh函数的梯度。
与Sigmoid函数相比,tanh函数的梯度更陡。 使用sigmoid函数还是tanh函数取决于问题陈述中对梯度的要求。 但是tanh函数出现了Sigmoid函数类似的问题,梯度渐趋平坦,并且值非常低。
ReLU函数
ReLU是近几年非常受欢迎的激活函数。其定义为:
f(x)=max(0,x)
以下是图形表示:
ReLU是如今设计神经网络时使用最广泛的激活函数。首先,ReLU函数是非线性的,这意味着我们可以很容易地反向传播误差,并激活多个神经元。
ReLU函数优于其他激活函数的一大优点是它不会同时激活所有的神经元。这是什么意思?如果输入值是负的,ReLU函数会转换为0,而神经元不被激活。这意味着,在一段时间内,只有少量的神经元被激活,神经网络的这种稀疏性使其变得高效且易于计算。
我们来看看ReLU函数的梯度。
ReLU函数也存在着梯度为零的问题。看上图,x<0时,梯度是零,这意味着在反向传播过程中,权重没有得到更新。这就会产生死神经元,而这些神经元永远不会被激活。好在当我们遇到问题时,我们总能找到解决方案。
Leaky ReLU函数
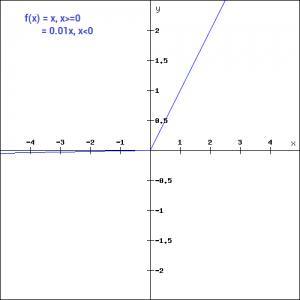
Leaky ReLU函数只是一个ReLU函数的改良版本。我们看到,在ReLU函数中,x < 0时梯度为0,这使得该区域的神经元死亡。为了解决这个问题, Leaky ReLU出现了。这是它的定义:
f(x)= ax, x<0
= x, x>=0
我们所做的,只是用一个非水平线简单地替换了水平线。这里a是一个很小的值,如0.01。见下图。
替换水平线的主要优点是去除零梯度。在这种情况下,上图左边的梯度是非零的,所以该区域的神经元不会成为死神经元。梯度图如下。
与Leaky ReLU函数类似的,还有PReLU函数,它的定义与Leaky ReLU相似。
f(x)= ax, x<0
= x, x>=0
然而, 在PReLU函数中,a也是可训练的函数。神经网络还会学习a的价值,以获得更快更好的收敛。 当Leaky ReLU函数仍然无法解决死神经元问题并且相关信息没有成功传递到下一层时,可以考虑使用PReLU函数。
Softmax函数
softmax函数也是一种sigmoid函数,但它在处理分类问题时很方便。sigmoid函数只能处理两个类。当我们想要处理多个类时,该怎么办呢?只对单类进行“是”或“不是”的分类方式将不会有任何帮助。softmax函数将压缩每个类在0到1之间,并除以输出总和。它实际上可以表示某个类的输入概率。其定义为:
比如,我们输入[1.2,0.9,0.75],当应用softmax函数时,得到[0.42,0.31,0.27]。现在可以用这些值来表示每个类的概率。
softmax函数最好在分类器的输出层使用。
如何选择正确的激活函数?
现在我们已经了解了这么多的激活函数,接下来就需要分析在哪种情况下应该使用哪种激活函数了。激活函数好或坏,不能凭感觉定论。然而,根据问题的性质,我们可以为神经网络更快更方便地收敛作出更好的选择。
用于分类器时,Sigmoid函数及其组合通常效果更好。
由于梯度消失问题,有时要避免使用sigmoid和tanh函数。
ReLU函数是一个通用的激活函数,目前在大多数情况下使用。
如果神经网络中出现死神经元,那么PReLU函数就是最好的选择。
请记住,ReLU函数只能在隐藏层中使用。
一点经验:你可以从ReLU函数开始,如果ReLU函数没有提供最优结果,再尝试其他激活函数。