线性判别分析LDA原理

线性判别分析LDA原理

线性判别分析LDA(Linear Discriminant Analysis)又称为Fisher线性判别，是一种监督学习的降维技术，也就是说它的数据集的每个样本都是有类别输出的，这点与PCA（无监督学习）不同。LDA在模式识别领域（比如人脸识别，舰艇识别等图形图像识别领域）中有非常广泛的应用，因此我们有必要了解下它的算法原理。

1. LDA的思想

LDA的思想是： 最大化类间均值，最小化类内方差。意思就是将数据投影在低维度上，并且投影后同种类别数据的投影点尽可能的接近，不同类别数据的投影点的中心点尽可能的远。

我们先看看最简单的情况。假设我们有两类数据 分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

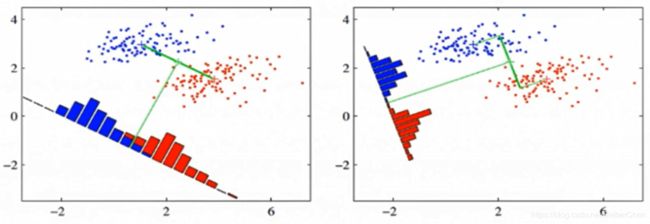
上图提供了两种投影方式，哪一种能更好的满足我们的标准呢？从直观上可以看出，右图要比左图的投影效果好，因为右图的黑色数据和蓝色数据各个较为集中，且类别之间的距离明显。左图则在边界处数据混杂。以上就是LDA的主要思想了，当然在实际应用中，我们的数据是多个类别的，我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面。

2. 瑞利商(Rayleigh quotient)与广义瑞利商(genralized Rayleigh quotient)

首先来看瑞利商的定义。瑞利商是指这样的函数$R(A,x)$:
$$R(A,x)=\frac{x^{H}Ax}{x^{H}x}$$
其中，$x$是非零向量，而$A$为$n\times n$的Hermitan矩阵。所谓的Hermitan矩阵就是满足共轭转置矩阵和自己相等的矩阵，即$A^H=A$，例如，$A=\left(\begin{array}{cc}1& 2+i\\ 2-i& 1\end{array}\right)$的共轭转置等于其本身。当$A$为实矩阵时，如果满足$A^T=A$，则$A$为Hermitan矩阵。

瑞利商$R(A,x)$有一个非常重要的性质，即它的最大值等于矩阵$A$最大的特征值，而最小值等于矩阵$A$的最小的特征值，也就是满足

$${\lambda }_{\min }\le \frac{x^{H}Ax}{x^{H}x}\le {\lambda }_{\max }$$

当向量$x$是标准正交基，即满足$x^{H}x=1$时，瑞利商退化为$R(A,x)=x^{H}Ax$。

下面看一下广义瑞利商。广义瑞利商是指这样的函数$R(A,B,x)$:
$$R(A,B,x)=\frac{x^{H}Ax}{x^{H}Bx}$$
其中x为非零向量，而$A,B$为$n\times n$的Hermitan矩阵。$B$为正定矩阵。它的最大值和最小值是什么呢？其实我们只要通过将其通过标准化就可以转化为瑞利商的格式。令$x=B^{-1/2}{x}^{\prime }$，则分母转化为：
$$x^{H}Bx=x^{\prime H}{\left(B^{-1/2}\right)}^{H}B{B}^{-1/2}{x}^{\prime }=x^{\prime H}{B}^{-1/2}B{B}^{-1/2}{x}^{\prime }=x^{\prime H}{x}^{\prime }$$
而分子转化为：
$$x^{H}Ax=x^{\prime H}{B}^{-1/2}A{B}^{-1/2}{x}^{\prime }$$
此时我们的$R(A,B,x)$转化为$R(A,B,x^{\prime })$:
$$R\left(A,B,x^{\prime }\right)=\frac{x^{\prime H}{B}^{-1/2}A{B}^{-1/2}{x}^{\prime }}{x^{\prime H}{x}^{\prime }}$$
利用前面的瑞利商的性质，我们可以很快的知道，$R(A,B,x^{\prime })$的最大值为矩阵$B^{-1/2}A{B}^{-1/2}$的最大特征值，或者说矩阵$B^{-1}A$的最大特征值，而最小值为矩阵$B^{-1}A$的最小特征值。

2. LDA的原理及推导过程

假设样本共有K类，每一个类的样本的个数分别为$N_1,N_2,...,N_k$
$x_1^1,x_1^2,...,x_1^{N_1}$对应第1类
$x_2^1,x_2^2,...,x_2^{N_2}$对应第2类
$x_k^1,x_k^2,...,x_k^{N_k}$对应第K类，其中每个样本$x_i^j$均为$n$维向量
设${\tilde{x}}_i^j$为$x_i^j$变化后的样本，则${\tilde{x}}_i^j=<x,u>u=|x||u|cos\theta \cdot u=\left(x^{T}u\right)u$

此处设$u$为单位向量，即$u^{T}u=1$.

假设第K类样本的数据集为$D_k$，变化后的样本的均值向量为：$\tilde{\mathrm{m}}=\frac{{\sum }_{\tilde{x}\in D_k}\tilde{x}}{N_k}$，那么，第K类样本的方差为$\frac{S_k}{N_k}$，其中：
$$\begin{array}{rl}{\mathrm{S}}_{\mathrm{k}}& =\sum _{\tilde{x}\in D_k}(\tilde{x}-\tilde{\mathrm{m}}{)}^T(\tilde{x}-\tilde{\mathrm{m}})\\ & =\sum _{x\in D_k}{\left[\left(x^{T}u\right)u-\left(m^{T}u\right)u\right]}^T\left[\left(x^{T}u\right)u-\left(m^{T}u\right)u\right]\\ & =\sum _{x\in D_k}\left[\left(x^{T}u\right)u^T-\left(m^{T}u\right)u^T\right]\left[\left(x^{T}u\right)u-\left(m^{T}u\right)u\right](x^{T}u，m^{T}u为实数,转置仍是本身)\\ & =\sum _{x\in D_k}\left[{\left(x^{T}u\right)}^2{u}^{T}u-2\left(x^{T}u\right)\left(m^{T}u\right)u^{T}u+{\left(m^{T}u\right)}^2{u}^{T}u\right]\\ & =\sum _{x\in D_k}\left[{\left(x^{T}u\right)}^2-2\left(x^{T}u\right)\left(m^{T}u\right)+{\left(m^{T}u\right)}^2\right]\end{array}$$
第K类样本的方差：
$$\begin{array}{rl}\frac{S_k}{N_k}& =\frac{{\sum }_{x\in D_k}{\left(x^{T}u\right)}^2}{N_k}-2\frac{{\sum }_{x\in D_k}{x}^T\left(u{m}^{T}u\right)}{N_k}+\frac{{\sum }_{x\in D_k}{\left(m^{T}u\right)}^2}{N_k}\\ & =\frac{{\sum }_{x\in D_k}{u}^{T}x{x}^{T}u}{N_k}-2\frac{{\sum }_{x\in D_k}{x}^T}{N_k}u{m}^{T}u+{\left(m^{T}u\right)}^2(注：\frac{{\sum }_{x\in D_k}{\left(m^{T}u\right)}^2}{N_k}=(m^{T}u{)}^2。因为m^{T}u与x无关)\\ & =u^T\frac{{\sum }_{x\in D_k}x{x}^T}{N_k}u-{\left(m^{T}u\right)}^2(注：\frac{{\sum }_{x\in D_k}{x}^T}{N_k}=m^T)\\ & =u^T\frac{{\sum }_{x\in D_k}x{x}^T}{N_k}u-u^{T}m{m}^{T}u\\ & =u^T\left(\frac{{\sum }_{x\in D_k}x{x}^T}{N_k}-m{m}^T\right)u\end{array}$$
各个类别的样本方差之和：
$$\begin{array}{rl}\sum _k\frac{S_k}{N_k}& =\sum _{k=1}^K{u}^T\left(\frac{{\sum }_{x\in D_k}x{x}^T}{N_k}-m_k{m}_k^T\right)u\\ & =u^T\sum _{k=1}^K(\frac{{\sum }_{x\in D_k}x{x}^T}{N_k}-m_k{m}_k^T)u\\ & =u^T{S}_{w}u\end{array}$$
其中，$S_w={\sum }_{k=1}^K(\frac{{\sum }_{x\in D_k}x{x}^T}{N_k}-m_k{m}_k^T)$，$S_w$一般被称为类内散度矩阵

不同类别$i,j$之间的中心距离：
$$\begin{array}{rl}{S}_{ij}& ={\left({\tilde{m}}_i-{\tilde{m}}_j\right)}^T\left({\tilde{m}}_i-{\tilde{m}}_j\right)\\ & =[(u^T{m}_i)u-(u^T{m}_j)u{]}^T[(m_i^{T}u)u-(m_j^{T}u)u]\\ & =[(u^T{m}_i)u^T-(u^T{m}_j)u^T][u(m_i^{T}u)-u(m_j^{T}u)]\\ & =u^T(m_i-m_j)u^{T}u(m_i^T-m_j^T)u\\ & =u^T\left(m_i-m_j\right){\left(m_i-m_j\right)}^{T}u\end{array}$$

所有类别之间的距离之和为：
$$\begin{array}{rl}\sum _{\genfrac{}{}{0ex}{}{i,j}{i̸=j}}{s}_{ij}& =u^T\sum _{\genfrac{}{}{0ex}{}{i,j}{i̸=j}}[(m_i-m_j)(m_i-m_j{)}^T]u\\ & =u^T{S}_{b}u\end{array}$$
其中，$S_b={\sum }_{\genfrac{}{}{0ex}{}{i,j}{i̸=j}}[(m_i-m_j)(m_i-m_j{)}^T]$，$S_b$一般被称为类间散度矩阵。

在已知条件下，$S_w,S_b$均可求出，LDA算法的目标是“类间距离尽可能大，类内方差尽可能小”，即最大化$u^T{S}_{b}u$,最小化$u^T{S}_{w}u$.

令$J(u)=\frac{u^T{S}_{b}u}{u^T{S}_{w}u}$,则目标函数为：
$$\max J(u)$$
为了使所求最大，可假设$u^T{S}_{w}u=1$，则问题转化为：
$$\begin{array}{l}\max u^T{S}_{b}u\\ s.t.u^T{S}_{w}u=1\end{array}$$
$$\begin{array}{rl}L(u,\lambda )& =u^T{S}_{b}u+\lambda \left(1-u^T{S}_{w}u\right)\\ \frac{\partial L}{\partial u}& =S_{b}u+S_b^{T}u-\lambda S_{w}u-\lambda S_w^{T}u\\ & =2(S_{b}u-\lambda S_{w}u)(因为S_b，S_w为对称矩阵)\\ & =0\Rightarrow S_{b}u=\lambda S_{w}u\end{array}$$

证明$S_b$为对称矩阵：
$$\begin{array}{rl}{S}_b^T& =(\sum _{\genfrac{}{}{0ex}{}{i,j}{i̸=j}}[(m_i-m_j)(m_i-m_j{)}^T]{)}^T\\ & =\sum _{\genfrac{}{}{0ex}{}{i,j}{i̸=j}}[(m_i-m_j)(m_i-m_j{)}^T{]}^T\\ & =\sum _{\genfrac{}{}{0ex}{}{i,j}{i̸=j}}[(m_i-m_j)(m_i-m_j{)}^T]\\ & =S_b\end{array}$$
所以，$S_b$为对称矩阵，同理可证明$S_w$为对称矩阵。

$$\begin{array}{l}{S}_w^{-1}{S}_{b}u=\lambda u\end{array}$$

计算矩阵$S_w^{-1}{S}_b$的最大的$d$个特征值和对应的$d$个特征向量$(w_1,w_2,...,w_d)$，得到投影矩阵$W=(w_1,w_2,...,w_d)$。

注意: (1)选取特征值时，如果一些特征值明显大于其他的特征值，则取这些取值较大的特征值，因为它们包含更多的数据分布的信息。相反，如果一些特征值接近于0，我们将这些特征值舍去。
(2)由于$W$是一个利用了样本类别得到的投影矩阵，因此它能够降维到的维度d的最大值为$K-1$。为什么不是$K$呢？因为$S_b$中每个$m_i-m_j$的秩均为1(因为$m_i$为1维向量).

由$R(AB)\le \min (R(A),R(B))$知，
$$R((m_i-m_j)(m_i-m_j{)}^T)=1$$
又 $\because$
$$\begin{gathered} S_b=\sum _{\genfrac{}{}{0ex}{}{i,j}{i̸=j}}[(m_i-m_j)(m_i-m_j{)}^T], \\ R(A+B)\le R(A)+R(B) \end{gathered}$$
$$\therefore R(S_b)\le K-1\Rightarrow R(S_w^{-1}{S}_b)\le K-1$$
$\therefore \lambda =0$对应的特征向量至少有$(K-(K-1))=1$个，也就是说$d$最大为$K-1$.

3. LDA算法流程

输入：数据集$D=(x_1,y_1),(x_2,y_2),...,(x_m,y_m)$,其中，任意样本$x_i$为$n$维向量，$y_i\in \{C_1,C_2,...,C_k\}$,降维到的维度为$d$.

输出：降维后的数据集$D^{\prime }$.

1. 计算类内散度矩阵$S_w$
2. 计算类间散度矩阵$S_b$
3. 计算矩阵$S_w^{-1}{S}_b$
4. 计算矩阵$S_w^{-1}{S}_b$的特征值与特征向量，按从小到大的顺序选取前$d$个特征值和对应的$d$个特征向量$(w_1,w_2,...,w_d)$，得到投影矩阵$W$.
5. 对样本集中的每一个样本特征$x_i$，转化为新的样本$z_i=W^T{x}_i$
6. 得到输出样本集$D^{\prime }=\{(z_1,y_1),(z_2,y_2),...,(z_m,y_m)\}$

4. LDA与PCA对比

LDA与PCA都可用于降维，因此有很多相同的地方，也有很多不同的地方

• 相同点：

  • 两者均可用于数据降维
  • 两者在降维时均使用了矩阵特征分解的思想
  • 两者都假设数据符合高斯分布

• 不同点：

  • LDA是有监督的降维方法，而PCA是无监督降维方法
  • 当总共有K个类别时，LDA最多降到K-1维，而PCA没有这个限制
  • LDA除了用于降维，还可以用于分类
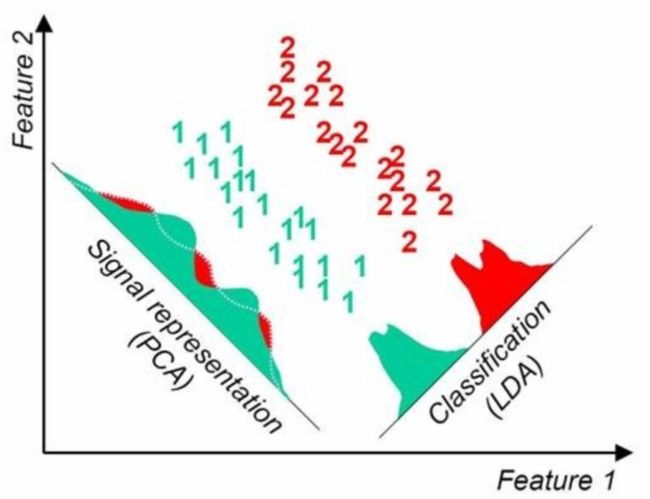
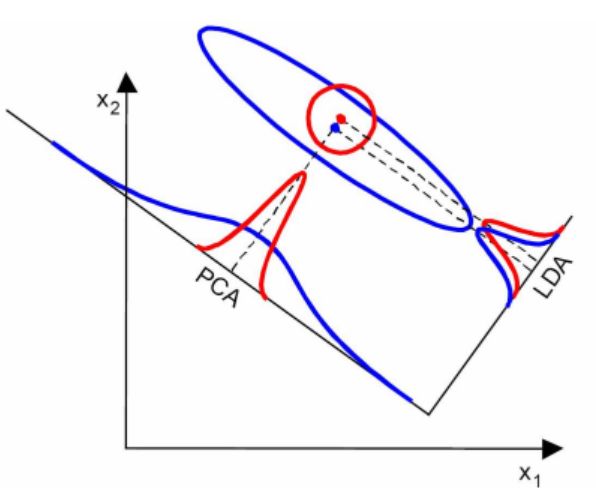
  • LCA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。这点可以从下图形象的看出，在某些数据分布下LDA比PCA降维较优（如下图的左图）。当然，某些数据分布下PCA比LDA降维较优（如下图的右图）。

图2

图3

5. LDA算法小结

LDA算法既可以用来降维，也可以用来分来，但是目前来说，LDA主要用于降维，在进行与图像识别相关的数据分析时，LDA是一个有力的工具。下面总结一下LDA算法的优缺点。

• LDA算法的优点
  • 在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习无法使用先验知识；
  • LDA在样本分类信息依赖均值而不是方差的时候，比PCA算法较优。
• LDA算法的缺点
  • LDA与PCA均不适合对非高斯分布样本进行降维
  • LDA降维算法最多降到类别数K-1的维度，当降维的维度大于K-1时，则不能使用LDA。当然目前有一些改进的LDA算法可以绕过这个问题
  • LDA在样本分类信息依赖方差而非均值的时候，降维效果不好
  • LDA可能过度拟合数据

参考：https://www.cnblogs.com/pinard/p/6244265.html