《强化学习》第二版 阅读随笔3
第三章 有限马尔可夫决策过程(finite Markov decision processes)
MDPs involve delayed reward and the need to tradeoff immediate and delayed reward. 马尔可夫决策与多臂老虎机问题相比,两者都需要在不同情况下选择不同的行为模式(action),但马尔可夫决策过程需要在既得利益和长远利益之间进行权衡。也就是决策之间不再是状态独立的,而是相互关联的(state-dependent)。
3.1 强化学习模型(agent)与环境之间的接口
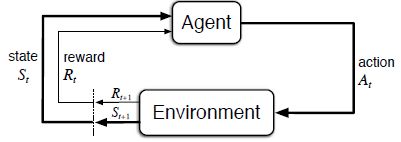 强化学习模型(agent)进行决策,以行为(action)作用于环境(environment),环境做出反馈,以奖励(reward)的形式反作用于模型。于此同时在客观上,模型所面临的环境已经被自己所改变,来到了一个新的状态(state)。模型始终以最大化价值(value)为目标,而价值就是奖励值的期望。
强化学习模型(agent)进行决策,以行为(action)作用于环境(environment),环境做出反馈,以奖励(reward)的形式反作用于模型。于此同时在客观上,模型所面临的环境已经被自己所改变,来到了一个新的状态(state)。模型始终以最大化价值(value)为目标,而价值就是奖励值的期望。
强化学习过程可以用以下序列来描述
![]()
- 在有限马尔可夫决策过程中,模型的行为模式(action),环境所做出的反馈(reward)以及整个系统所处的状态(state)都是有限的。模型所处的状态 S t S_t St以及获得的奖励值 R t R_t Rt都可以用离散的概率值来表示。
- 如下条件概率可以用来表示单步的状态更新和奖励反馈情况。
p ( s ′ , r ∣ s , a ) = P r ( S t = s ′ , R t = r ∣ S t − 1 = s , A t − 1 = a ) p(s',r|s,a)=Pr(S_t=s',R_t=r|S_{t-1}=s,A_{t-1}=a) p(s′,r∣s,a)=Pr(St=s′,Rt=r∣St−1=s,At−1=a)
即,下一状态 s ′ s' s′和agent取得的奖励 r r r,取决于当前状态 s s s和agent采取的行动 a a a。进一步来说当前 S t , R t S_t,R_t St,Rt仅取决于上一步 S t − 1 , A t − 1 S_{t-1},A_{t-1} St−1,At−1,而不直接取决于之前经历的所有强化学习模型(agent)与环境的交互情况。这就是俗话说“好了伤疤忘了疼”?但其实并不是这样,状态(state)本身必须要包含之前模型与环境交互的所有信息,这样的状态(state)我们称之为具有马尔可夫性质(Markov property)。 - 正如上文所述, s ′ , s ∈ S , r ∈ R , a ∈ A ( s ) s',s\in{S},r\in{R,a\in{A(s)}} s′,s∈S,r∈R,a∈A(s)。
- 根据对上文的理解,我们也可以得到如下结论:
-
p ( s ′ , r ∣ s , a ) = P r ( S t = s ′ , R t = r ∣ S t − 1 = s , A t − 1 = a ) p(s',r|s,a)=Pr(S_t=s',R_t=r|S_{t-1}=s,A_{t-1}=a) p(s′,r∣s,a)=Pr(St=s′,Rt=r∣St−1=s,At−1=a),使用这个4变量的动态方程(dynamics function),我们可以得到环境中其他有用的信息:
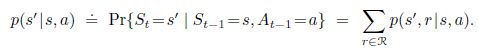
对下一状态的预测
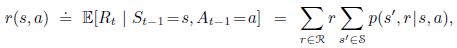 当前状态获得奖励(reward)的期望
当前状态获得奖励(reward)的期望
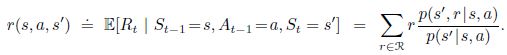
-
The general rule we follow is that anything that cannot be changed arbitrarily by the agent is considered to be outside of it and thus part of its environment.The agent–environment boundary represents the limit of the agent’s absolute control, not of its knowledge. 学习主体(agent)与环境(environment)之间的关系并不是简单的物理界限,环境对于学习主体来说往往是难于改变的,并且不是绝对受控的。以人来做比,agent类似于人的灵魂和思维,而环境则是人的肢体,周围真实存在的物体以及种种其他外界因素。
3.2 目标和奖励
上文中,我们提到,强化学习是目标导向的,这个目标就是最大化奖励(reward)期望,使强化学习模型能获得最大的累积奖励,而不是简单的贪心思想,这在前面已经反复提及。奖励信号是环境给模型的反馈,是设计模型所要达到现实目的抽象,而将现实问题用奖励函数进行规范化是强化学习的一大特点。
奖励(reward)的设计需要于现实目的保持一致,最大化奖励期望的过程就是模型学习如何更好地完成既定现实任务的过程。
奖励函数对于模型而言是一个“只看重结果,不关心过程”的评判,奖励函数的设计不应该试图加入有助于完成任务的先验知识。以下棋为例,不应为“吃子”或“占据主动优势”而给予模型奖励(尽管先验知识告诉我们这些都是有助于最终获胜的中间过程)。因为这样的奖励函数可能会误导模型本末倒置,“想尽办法”去“吃子”而不以最终的获胜为目标,因为这时候模型认为“吃子”比遥遥无期的所谓获胜更“划算”。这些先验知识应该由模型自己去摸索,你需要做的就是通过奖励函数告诉模型你想要让它做什么。
3.3 问题本身的周期性(Returns and Episodes)
上文我们反复提到,强化学习的最终目的是最大化奖励(reward)的累加值,也就是我们下文所提到的期望回报(expected return),用符号 G t G_t Gt表示。
- 周期性任务(episodic task,或者叫章节性任务),是指能够在有限的步骤内自行终止的任务,例如迷宫、下棋等。这些任务每一轮的结果都是相互独立的,任务结束后可以回到原点重新开始。那么这种任务中强化学习模型所获取的奖励为:
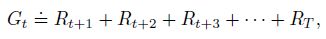 其中 T T T是指有限的步数, T T T的大小可以是不确定的变量; R T R_T RT则被称为终止状态(terminal state)。
其中 T T T是指有限的步数, T T T的大小可以是不确定的变量; R T R_T RT则被称为终止状态(terminal state)。 - 连续性任务(continuing task),是指那些正常情况不会自动终止的任务,例如长生命周期的机器人。此时如果再按照之前的思路对奖励值进行累加,那么期望回报 G t G_t Gt最终都会变为无穷大而无法处理,换句话说,我们无法处理无限的数据。我们只能摒弃之前"先知"式的假设,去预判有限的未来,引入折扣系数(discount rate) γ \gamma γ,奖励的期望可以表示为:
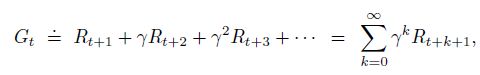 式中 γ ∈ [ 0 , 1 ] \gamma\in[0,1] γ∈[0,1],距离当前状态 S t S_t St越远的未来,强化学习模型所预判的奖励 R R R在期望回报 G G G中的比重会成指数衰减。这样的计算方式符合我们的生活经验同时也可以保证在 γ < 1 \gamma<1 γ<1时,权重总会衰减到0,从而获得有限的期望回报。当 γ = 0 \gamma=0 γ=0时,模型将表现为贪心思想,仅考虑最大化下一步的奖励值,随着 γ \gamma γ趋近于1,模型的眼光也会逐渐放长远。
式中 γ ∈ [ 0 , 1 ] \gamma\in[0,1] γ∈[0,1],距离当前状态 S t S_t St越远的未来,强化学习模型所预判的奖励 R R R在期望回报 G G G中的比重会成指数衰减。这样的计算方式符合我们的生活经验同时也可以保证在 γ < 1 \gamma<1 γ<1时,权重总会衰减到0,从而获得有限的期望回报。当 γ = 0 \gamma=0 γ=0时,模型将表现为贪心思想,仅考虑最大化下一步的奖励值,随着 γ \gamma γ趋近于1,模型的眼光也会逐渐放长远。 - 问题的周期性(episodic)和连续性(continuing)需要具体问题具体分析。如果假定一款游戏判定玩家操作失误后重新开始,通常来说,这是一个周期性问题,对于一般玩家而言,失误是难以避免的。但是如果让机器人去玩同一款游戏,可能永远都不会失误,这样就就变成了连续性问题。
3.4 章节性任务与连续性任务的统一表示方式(Unified Notation for Episodic and Continuing Tasks)
我们希望能够统一章节性任务(episodic task)与连续性任务(continuing task)的数学表示方式。
 对于章节性任务而言,任务总会在有限的步骤内结束,任务结束后,奖励信号(reward)自然也会归0,不会对回报(return)的累加值构成任何影响。所以我们可以统一用上面的公式表示两种类型的任务。其中折扣系数(discount rate) γ \gamma γ在表示章节任务时可以为1,具体原因在之前已经提及。
对于章节性任务而言,任务总会在有限的步骤内结束,任务结束后,奖励信号(reward)自然也会归0,不会对回报(return)的累加值构成任何影响。所以我们可以统一用上面的公式表示两种类型的任务。其中折扣系数(discount rate) γ \gamma γ在表示章节任务时可以为1,具体原因在之前已经提及。
上面这个式子我们可以用递归的思路来描述:
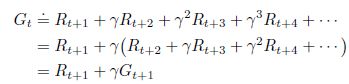 下面再仔细体会这样一个递归表示形式,首先 G t G_t Gt表示的是对未来回报值的期望值,我们(或者说强化学习模型)总希望能在未来获得高收益,当 γ = 0 \gamma=0 γ=0,模型将遵从贪心算法的思想,变得十分短视,反之,模型会将会把下一步 s t + 1 s_{t+1} st+1的收益期望 G t + 1 G_{t+1} Gt+1也考虑在内。
下面再仔细体会这样一个递归表示形式,首先 G t G_t Gt表示的是对未来回报值的期望值,我们(或者说强化学习模型)总希望能在未来获得高收益,当 γ = 0 \gamma=0 γ=0,模型将遵从贪心算法的思想,变得十分短视,反之,模型会将会把下一步 s t + 1 s_{t+1} st+1的收益期望 G t + 1 G_{t+1} Gt+1也考虑在内。
3.5 策略和价值函数(Policies and Value Functions)
- 价值函数(value functions)用于模型对特定状态(state)下行为模式(action)的评估。价值函数是模型未来获取奖励(reward)的期望值。
- 策略(policy)是指强化学习模型对某种行为(action)的偏好,是从状态(state)到具体行动(action)的映射,数学表示为: π ( a ∣ s ) \pi(a|s) π(a∣s)。
价值函数使用符号 v π ( s ) v_{\pi}(s) vπ(s)与当前状态 s s s(state)有关,与模型的行为策略 π \pi π(policy)有关。价值函数的值是模型未来回报(奖励的累加)的期望,数学语言表达如下:
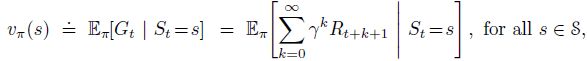
上式被称为状态-价值函数(state-value function),即代表从状态 s s s到价值期望的映射关系。式中 t t t是学习经历的步数, v π v_{\pi} vπ是策略 π \pi π的价值函数。
进一步,如果我们采取行动 a a a,那么行动-价值函数(action-value function)可以表示成:

行动-价值函数在状态-价值函数的基础上增加了行为方式(action) A t = a A_t=a At=a的前提条件。
蒙特卡罗方法
试想,无论是 v π ( s ) v_\pi(s) vπ(s)还是 q π ( s , a ) q_\pi(s,a) qπ(s,a),只要模型试错的次数足够多,我们为任意状态(state)或行为(action)的回报值(reward)做平均,最后一定会收敛到其真实值,这个过程类似于人类“实践经验”积累的过程。
当然,对于一些应用场景中我们无法穷举所有的状态(例如围棋),但是我们可以使用参数方程(parameterized function)来对 q π ( s , a ) q_\pi(s,a) qπ(s,a)和 v π ( s ) v_\pi(s) vπ(s)进行估计,根据模型获得的”经验“(历史样本)调整参数方程中的参数(参数的数量小于实际状态数)来拟合回报值。
递归
在3.4节中曾经提到,无论是章节性任务还是连续性任务,其回报值的期望都可以被公式统一表达,并且还有一个递归形式的表示: G t = R t + 1 + γ G t + 1 G_t=R_{t+1}+{\gamma}G_{t+1} Gt=Rt+1+γGt+1
那么对于状态-价值函数(state-value function)也可以找到递归的表示。我们首先要明确,状态-价值函数是回报 G t G_t Gt在该状态(s)下采取所有可能行为模式(a)所获取回报的期望值,即 v π ( s ) = E π ( G t ∣ S t = s ) v_\pi(s)=E_\pi(G_t|S_t=s) vπ(s)=Eπ(Gt∣St=s)
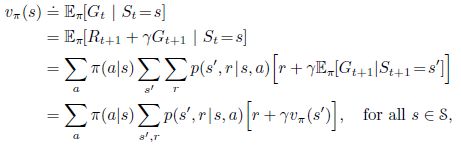
式中 ∑ a π ( a ∣ s ) \sum_{a}\pi(a|s) ∑aπ(a∣s)表达的就是对状态 s s s下所有可能行为模式 a a a的遍历。 ∑ s ′ ∑ r p ( s ′ , r ∣ s , a ) \sum_{s'}\sum_{r}p(s', r| s, a) ∑s′∑rp(s′,r∣s,a)显然遍历了在当前状态 s s s下采取行为 a a a将可能来到的下一状态 s ′ s' s′和对应的回报 r r r。综上,我们不难发现,状态-价值函数中三个重要的自变量 a , s ′ , r a,s',r a,s′,r,我们遍历了这三个变量的所有取值。三个变量取值产生的组合,每种可能的概率可以表示为 π ( a ∣ s ) p ( s ′ , r ∣ s , a ) \pi(a|s)p(s', r|s, a) π(a∣s)p(s′,r∣s,a),所以任意状态下的状态-价值函数可以理解为中括号中内容 [ r + γ v π ( s ′ ) ] [r+\gamma{v_\pi(s')}] [r+γvπ(s′)]的加权和。
贝尔曼方程
上面推导的关于状态价值函数 v π v_\pi vπ的递归表达式就是 v π v_\pi vπ的贝尔曼恒等式(Bellman equation) v π ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ , r p ( s ′ , r ∣ s , a ) [ r + γ v π ( s ′ ) ] v_\pi(s)=\sum_a\pi(a|s)\sum_{s', r}p(s',r|s,a)[r+\gamma{v_\pi(s')}] vπ(s)=a∑π(a∣s)s′,r∑p(s′,r∣s,a)[r+γvπ(s′)]
贝尔曼恒等式表达了当前状态(state)的价值(value,即奖励值的期望)与下一状态价值之间的关系
备份图
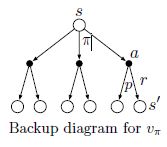
图中空心圆环表示状态,实心圆点表示一对状态和行为(state-action pair)。与卷积神经网络反向传播相类似,强化学习中也需要将价值(value)信息从下一状态 s ′ s' s′反向更新到前一状态 s s s对应的状态-行为节点(state-action pair)上。值得注意的是,与转换图(transition graphs)不同的是,备份图中的节点可以表示相同的状态(有环?)。
最优策略和最优价值函数(Optimal Policies and Optimal Value Functions)
所谓最优策略就是能让模型获取最大的收益,当策略 π \pi π的回报期望在所有状态(state)下都等于或优于 π ′ \pi' π′我们认为 π \pi π更优。从状态-价值函数的角度来说有: v π ( s ) ≥ v π ′ ( s ) ; s ∈ S v_\pi(s)\geq{v_{\pi'}(s)};s\in{S} vπ(s)≥vπ′(s);s∈S进一步,最优的策略 π \pi π总能使状态价值函数的值最大化: v ∗ ( s ) = max π v π ( s ) v_{*}(s)=\max_{\pi}v_\pi(s) v∗(s)=πmaxvπ(s)
对于行动价值函数 q ( a , s ) q(a, s) q(a,s),上文提到,行动-价值函数基于状态-价值函数

上式可以进一步化成如下形式:
![]() 可见,如果状态-价值函数通过策略 π \pi π取最优,那么对应的行为-价值函数同样是最优的。
可见,如果状态-价值函数通过策略 π \pi π取最优,那么对应的行为-价值函数同样是最优的。
贝尔曼优化方程
最优化状态-价值函数
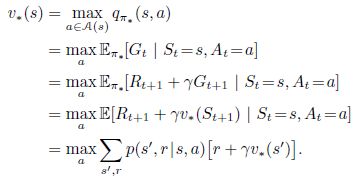 最优化状态-价值函数就是要选取令当前状态的行为-价值函数最大化的行为 a a a。
最优化状态-价值函数就是要选取令当前状态的行为-价值函数最大化的行为 a a a。
最优化行为-价值函数

与原式做对比可以发现,这里用最大化的下一状态 s ′ s' s′的行为-价值函数替代了原有的回报值 R t R_t Rt的衰减累加,最优化行为-价值函数就是要找到使下一状态 s ′ s' s′最大化 q ∗ ( s ′ , a ′ ) q_*(s',a') q∗(s′,a′)的 a ′ a' a′。
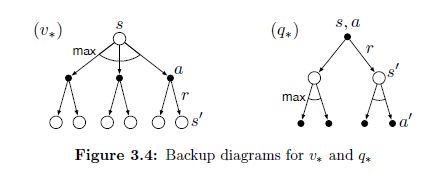 通过观察最优化方程的备份图可以看出,对于状态-价值函数,优化方向为最大化 q ( s , a ) q(s,a) q(s,a);对于行为-价值函数,优化方向为最大化 q ( s ′ , a ′ ) q(s',a') q(s′,a′)。
通过观察最优化方程的备份图可以看出,对于状态-价值函数,优化方向为最大化 q ( s , a ) q(s,a) q(s,a);对于行为-价值函数,优化方向为最大化 q ( s ′ , a ′ ) q(s',a') q(s′,a′)。
贝尔曼优化方程都聚焦于寻找在下一阶段最大化回报的行为 a 或 a ′ a或a' a或a′,这是一种贪心的思想,但优化方程的美妙之处在于在最优化下一状态的同时兼顾了未来总体回报的最大化。再次回顾行为价值-函数 q ( a , s ) q(a,s) q(a,s)和状态-价值函数 v ( s ) v(s) v(s)可以发现,两者本身都兼顾了未来总体收益(reward)的最大化,而贝尔曼优化方程所表达的是两个价值方程在状态之间的递归关系。
3.7 最优和近似(Optimality and Approximation)
通过上面的最优化方程来选取各个状态下的行为模式 a a a需要对所有情况进行穷举,从而选出其中的最大值。对于一些稍微复杂的问题,每一次状态(state)变化所产生的计算量都是不可接受的。穷举所有可能的情况也将需要巨大的内存空间。我们所使用的强化学习方法迫使我们不得不近似,去忽略出现概率低的情况。因为强化学习是一个实时的过程,我们可以让模型投入更多的经历在出现概率高的情况。这是强化学习与其他马尔可夫决策过程的解决方案有所不同的地方。
3.8 总结
-
Reinforcement learning is about learning from interaction how to behave in order to achieve a goal.
-
Everything inside the agent is completely known and controllable by the agent; everything outside is incompletely controllable but may or may not be completely known(环境).
-
A policy is a stochastic rule by which the agent selects actions as a function of states. The agent’s objective is to maximize the amount of reward it receives over time.
-
The return is the function of future rewards that the agent seeks to maximize (in expected value).
-
A policy’s value functions assign to each state(状态-价值函数), or state–action pair(行为-价值函数), the expected return from that state, or state–action pair, given that the agent uses the policy.
-
A policy’s value functions assign to each state, or state–action pair, the expected return from that state, or state–action pair, given that the agent uses the policy. The optimal value functions assign to each state, or state–action pair, the largest expected return achievable by any policy. A policy whose value functions are optimal is an optimal policy. Whereas the optimal value functions for states and state–action pairs are unique for a given MDP, there can be many optimal policies. Any policy that is greedy with respect to the optimal value functions must be an optimal policy. The Bellman optimality equations are special consistency conditions that the optimal value functions must satisfy and that can, in principle, be solved for the optimal value functions, from which an optimal policy can be determined with relative ease.
如果agent使用策略,则策略的价值函数将从该状态或状态操作对(state-action pair)获得的期望返回值分配给每个状态或状态操作对。 将最优值函数分配给每个状态或状态操作对,这是任何策略可以获得的最大预期收益。价值函数最优的策略就是最优策略。虽然对于给定的MDP,状态和状态操作对的最优值函数是惟一的,但是可以有许多最优策略。 任何对最优价值函数贪婪的策略必须是最优策略。Bellman最优性方程是最优值函数必须满足的特殊一致性条件,原则上可以求解最优值函数,从而相对容易地确定最优策略。 -
In reinforcement learning we are very much concerned with cases in which optimal solutions cannot be found but must be approximated in some way.