BZOJ 3995 SDOI2015 道路修建

一道考试上难得A的题目……

提示：
1. 做过BZOJ1018吗 ， 其实一样的思路啊……
2. 某数据结构能维护联通性 ， 其实此题没什么新意啊QAQ

详细题解代码后：

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

__inline int re() {
    int n = 0, ch = getchar(); bool flag = false;
    while(!isdigit(ch)) flag |= ch == '-', ch = getchar();
    while(isdigit(ch)) n = n * 10 + ch - '0', ch = getchar();
    return flag ? -n : n;
}

const int maxn = 6e4+1e2;
const int INF = 0x3f3f3f3f;

int n , m;
int u[maxn][2] , d[maxn][2] , l[maxn][2] , r[maxn][2];
int seg[maxn*8][5];

void up(int& a , int b) { a = min(a , b); }

void maintain(int a[5] , int l[5] , int r[5] , int mn , int sm)
{
    memset(a , INF , sizeof(seg[0]));

    up(a[0] , l[0] + r[0] + mn);
    up(a[1] , l[0] + r[1] + mn);
    up(a[0] , l[0] + r[2] + sm);
    up(a[0] , l[0] + r[3] + sm);
    up(a[1] , l[0] + r[3] + mn);
    up(a[1] , l[0] + r[4] + sm);

    up(a[0] , l[1] + r[0] + sm);
    up(a[1] , l[1] + r[1] + sm);
    up(a[1] , l[1] + r[3] + sm);

    up(a[2] , l[2] + r[0] + mn);
    up(a[4] , l[2] + r[1] + mn);
    up(a[2] , l[2] + r[2] + sm);
    up(a[2] , l[2] + r[3] + sm);    
    up(a[4] , l[2] + r[3] + mn);    
    up(a[4] , l[2] + r[4] + sm);    

    up(a[0] , l[3] + r[0] + sm);
    up(a[1] , l[3] + r[1] + sm);
    up(a[4] , l[3] + r[1] + mn);
    up(a[3] , l[3] + r[3] + sm);
    up(a[4] , l[3] + r[3] + mn);
    up(a[4] , l[3] + r[4] + sm);

    up(a[2] , l[4] + r[0] + sm);
    up(a[4] , l[4] + r[1] + sm);
    up(a[4] , l[4] + r[3] + sm);
}

void build(int o , int l , int r)
{
    if(l==r)
    {
        seg[o][0] = d[l][0];
//      seg[o][1] = seg[o][2] = INF;
        return;
    }
    else 
    {
        int mid = (l+r)/2 , lson = o*2 , rson = lson+1;
        build(lson , l , mid);
        build(rson , mid+1 , r);

        int mn = min(::r[mid][0] , ::r[mid][1]) , sm = ::r[mid][1]+::r[mid][0];
        maintain(seg[o] , seg[lson] , seg[rson] , mn , sm);
    }
}

void query(int o , int l , int r , int L , int R , int res[5])
{
    if(L <= l && r <= R)   memcpy(res , seg[o] , sizeof(seg[o]));
    else 
    {
        int mid = (l+r)/2 , lson = o*2 , rson = lson+1 , r1[5] , r2[5];
        int mn = min(::r[mid][0] , ::r[mid][1]) , sm = ::r[mid][1]+::r[mid][0];
        if(L <= mid)
        {
            if(R > mid)
            {
                query(lson , l , mid , L , R , r1);
                query(rson , mid+1 , r , L , R , r2);
                maintain(res , r1 , r2 , mn , sm);
            }
            else query(lson , l , mid , L , R , res);
        }
        else query(rson , mid+1 ,r , L , R , res);
    }
}

void modify(int o , int l , int r , int L , int R)
{
    if(L <= l && r <= R)
    {
        if(l==r)
        {
            seg[o][0] = d[l][0];
            return;
        }
        else 
        {
            int mid = (l+r)/2;
            int mn = min(::r[mid][0] , ::r[mid][1]) , sm = ::r[mid][1]+::r[mid][0];
            maintain(seg[o] , seg[o*2] , seg[o*2+1] , mn , sm);
        }
    }
    else 
    {
        int mid = (l+r)/2 , lson = o*2 , rson = o*2+1;
        int mn = min(::r[mid][0] , ::r[mid][1]) , sm = ::r[mid][1]+::r[mid][0];
        if(L <= mid) modify(lson , l , mid , L , R);
        if(R >  mid) modify(rson , mid+1 , r , L , R);

        maintain(seg[o] , seg[lson] , seg[rson] , mn , sm);
    }
}

int main()
{
    cin>>n>>m;
    for(int i=1;iint v = re();
        r[i][0] = l[i+1][0] = v;
    }

    for(int i=1;iint v = re();
        r[i][1] = l[i+1][1] = v;
    }

    for(int i=1;i<=n;i++)
    {
        int v = re();
        u[i][1] = d[i][0] = v;
    }

    build(1 , 1 , n);

    while(m--)
    {
        int a[5];
        char s[2];
        scanf("%s" , s);
        if(s[0] == 'Q')
        {
            int s = re() , t = re();
            query(1 , 1 , n , s , t , a);
            printf("%d\n" , a[0]);
        }
        else
        {
            int x1 = re() , y1 = re() , x2 = re() , y2 = re() , v = re();
            x1--; x2--;
            if(x1 == x2)
            {
                if(y1 > y2) swap(y1 , y2);
                r[y1][x1] = l[y2][x1] = v;
                modify(1 , 1 , n , y1 , y2);
            }
            else 
            {
                u[y1][1] = d[y1][0] = v;
                modify(1 , 1 , n , y1 , y1);
            }
        }
    }

    return 0;
}

线段树嘛……
有一个结论 ， 任何时刻一个块必须与四个角落中的某一块相连 ， 此时只有5种情形 ， 如下图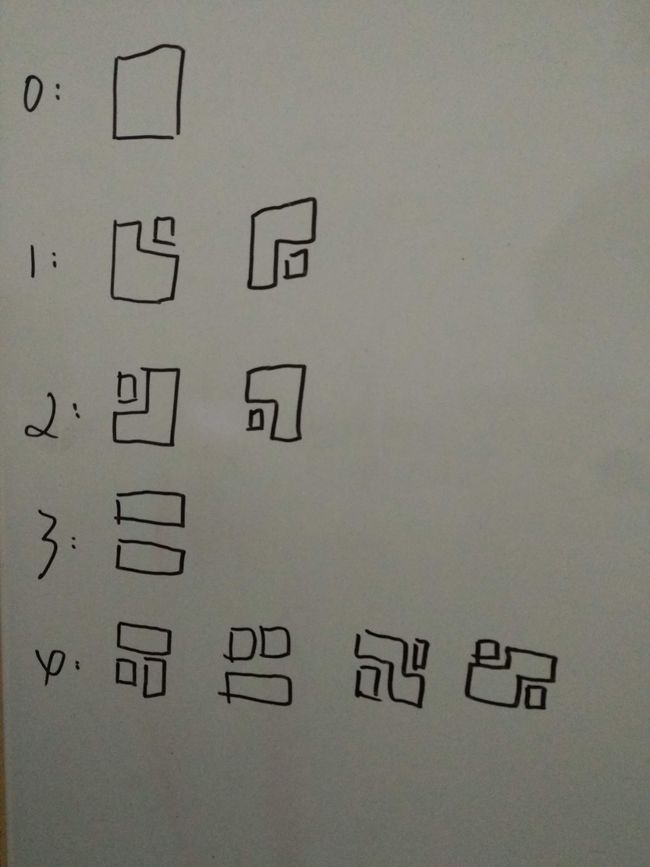
此时显然转移就是把两块拼起来 ， 种类繁多但其实并不麻烦