机器学习数学|偏度与峰度及其python实现

矩

• 对于随机变量X,X的K阶原点矩为

  E(Xk)E(Xk)

• X的K阶中心矩为

  E([X−E(X)]k)E([X−E(X)]k)

• 期望实际上是随机变量X的1阶原点矩,方差实际上是随机变量X的2阶中心矩
• 变异系数(Coefficient of Variation):标准差与均值(期望)的比值称为变异系数,记为C.V
• 偏度Skewness(三阶)
• 峰度Kurtosis(四阶)

偏度与峰度

利用matplotlib模拟偏度和峰度

计算期望和方差

import matplotlib.pyplot as plt
import math
import numpy as np
def calc(data):
    n=len(data) # 10000个数
    niu=0.0 # niu表示平均值,即期望.
    niu2=0.0 # niu2表示平方的平均值
    niu3=0.0 # niu3表示三次方的平均值
    for a in data:
        niu += a
        niu2 += a**2
        niu3 += a**3
    niu /= n  
    niu2 /= n
    niu3 /= n
    sigma = math.sqrt(niu2 - niu*niu)
    return [niu,sigma,niu3]

• niu=Xi¯即期望niu=Xi¯即期望

• niu2=∑ni=1X2inniu2=∑i=1nXi2n

• niu3=∑ni=1X3inniu3=∑i=1nXi3n

• sigma表示标准差公式为

  σ=E(x2)−E(x)2−−−−−−−−−−−−√σ=E(x2)−E(x)2

  用python语言表示即为sigma=math.sqrt(niu2−niu∗niu)用python语言表示即为sigma=math.sqrt(niu2−niu∗niu)

• 返回值为[期望,标准差,E(x3)E(x3)]
• PS:我们知道期望E(X)的计算公式为

  E(X)=∑i=1np(i)x(i)−−−−−(1)E(X)=∑i=1np(i)x(i)−−−−−(1)

  这里我们X一个事件p(i)表示事件出现的概率,x(i)表示事件所给予事件的权值.
• 我们直接利用

  E(x)=Xi¯−−−−(2)E(x)=Xi¯−−−−(2)

  表示期望应当明确 
  1. (2)公式中Xi是利用numpy中的伪随机数生成的,其均值用于表示期望Xi是利用numpy中的伪随机数生成的,其均值用于表示期望
  2. 此时(1)公式中对事件赋予的权值默认为1,即公式的本来面目为

     E(x)=(Xi∗1)¯E(x)=(Xi∗1)¯

计算偏度和峰度

def calc_stat(data):
    [niu, sigma, niu3]=calc(data)
    n=len(data)
    niu4=0.0 # niu4计算峰度计算公式的分子
    for a in data:
        a -= niu
        niu4 += a**4
    niu4 /= n

    skew =(niu3 -3*niu*sigma**2-niu**3)/(sigma**3) # 偏度计算公式
    kurt=niu4/(sigma**4) # 峰度计算公式:下方为方差的平方即为标准差的四次方
    return [niu, sigma,skew,kurt]

利用matplotlib模拟图像

if __name__ == "__main__":
    data =  list(np.random.randn(10000)) # 满足高斯分布的10000个数
    data2 = list(2*np.random.randn(10000))  # 将满足好高斯分布的10000个数乘以两倍,方差变成四倍
    data3 =[x for x in data if x>-0.5] # 取data中>-0.5的值
    data4 = list(np.random.uniform(0,4,10000)) # 取0~4的均匀分布
    [niu, sigma, skew, kurt] = calc_stat(data)
    [niu_2, sigma2, skew2, kurt2] = calc_stat(data2)
    [niu_3, sigma3, skew3, kurt3] = calc_stat(data3)
    [niu_4, sigma4, skew4, kurt4] = calc_stat(data4)
    print (niu, sigma, skew, kurt)
    print (niu2, sigma2, skew2, kurt2)
    print (niu3, sigma3, skew3, kurt3)
    print (niu4, sigma4, skew4, kurt4)
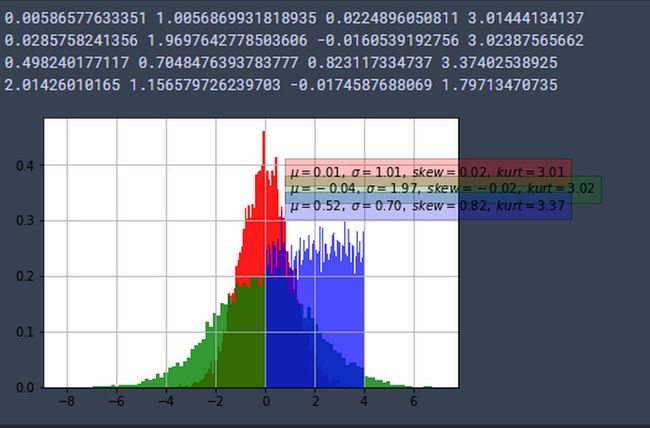
    info = r'$\mu=%.2f,\ \sigma=%.2f,\ skew=%.2f,\ kurt=%.2f$' %(niu,sigma, skew, kurt) # 标注
    info2 = r'$\mu=%.2f,\ \sigma=%.2f,\ skew=%.2f,\ kurt=%.2f$' %(niu_2,sigma2, skew2, kurt2)
    info3 = r'$\mu=%.2f,\ \sigma=%.2f,\ skew=%.2f,\ kurt=%.2f$' %(niu_3,sigma3, skew3, kurt3)
    plt.text(1,0.38,info,bbox=dict(facecolor='red',alpha=0.25))
    plt.text(1,0.35,info2,bbox=dict(facecolor='green',alpha=0.25))
    plt.text(1,0.32,info3,bbox=dict(facecolor='blue',alpha=0.25))
    plt.hist(data,100,normed=True,facecolor='r',alpha=0.9)
    plt.hist(data2,100,normed=True,facecolor='g',alpha=0.8)
    plt.hist(data4,100,normed=True,facecolor='b',alpha=0.7)
    plt.grid(True)
    plt.show()

• 

• 图形表示的是利用numpy随机数生成函数生成的随机数的统计分布,利用matplotlib.pyplot.hist绘制的直方图.即是出现数字的分布统计,并且是归一化到0~1区间后的结果.
• 即横轴表示数字,纵轴表示在1000个随机数中横轴对应的数出现的百分比.若不使用归一化横轴表示数字(normed=False),纵轴表示出现的次数.
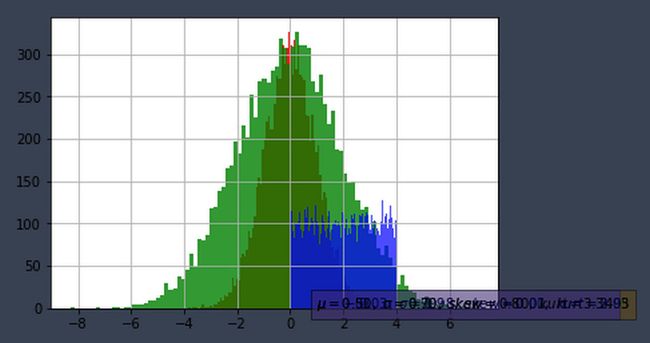
• 若不使用归一化–纵轴表示出现次数

• 关于matplotlib.pyplot.hist函数

n, bins, patches = plt.hist(arr, bins=10, normed=0, facecolor='black', edgecolor='black',alpha=1，histtype='b')
hist的参数非常多，但常用的就这六个，只有第一个是必须的，后面四个可选

arr: 需要计算直方图的一维数组

bins: 直方图的柱数，可选项，默认为10

normed: 是否将得到的直方图向量归一化。默认为0

facecolor: 直方图颜色

edgecolor: 直方图边框颜色

alpha: 透明度

histtype: 直方图类型，‘bar’, ‘barstacked’, ‘step’, ‘stepfilled’

返回值 ：

n: 直方图向量，是否归一化由参数normed设定

bins: 返回各个bin的区间范围

patches: 返回每个bin里面包含的数据，是一个list

•  

关于matplotlib.pyplot.hist函数