QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning笔记

QMIX: Monotonic Value Function Factorisation for Deep Multi-Agent Reinforcement Learning

1. 论文讲了什么/主要贡献是什么

在多代理强化学习中，存在代理单独计算价值函数和完全集中计算价值函数两种方式，前者存在不稳定的问题，后者存在可扩展性差的问题（维度灾难）。作者在介于两者之前的VDN算法的基础上，对从单代理价值函数到中心价值函数之间的映射关系进行了改进，在映射的过程中将原来的线性映射换为非线性映射，并通过超网络的引入将额外状态信息加入到决策过程，提高了模型性能。

2. 论文摘要：

In many real-world settings, a team of agents must coordinate their behaviour while acting in a decentralised way. At the same time, it is often possible to train the agents in a centralised fashion in a simulated or laboratory setting, where global state information is available and communication constraints are lifted. Learning joint actionvalues conditioned on extra state information is an attractive way to exploit centralised learning, but the best strategy for then extracting decentralised policies is unclear. Our solution is QMIX, a novel value-based method that can train decentralised policies in a centralised end-to-end fashion. QMIX employs a network that estimates joint action-values as a complex non-linear combination of per-agent values that condition only on local observations. We structurally enforce that the joint-action value is monotonic in the per-agent values, which allows tractable maximisation of the joint action-value in off-policy learning, and guarantees consistency between the centralised and decentralised policies. We evaluate QMIX on a challenging set of StarCraft II micromanagement tasks, and show that QMIX significantly outperforms existing value-based multi-agent reinforcement learning methods.

在许多实际环境中，一组代理必须协调它们的行为，同时以一种去中心化的方式行动。 同时，在仿真或实验室环境中以集中的方式训练代理是可能的，在这种环境下，能够获得全局状态信息并且不再存在通信限制。以额外的状态信息为条件的联合动作价值学习是利用集中学习的一种有吸引力的方式，但随后提取分散政策的最佳策略还不清楚。我们的解决方案是QMIX，这是一种基于价值的新方法，可以以集中的端到端方式训练去中心化的策略。QMIX使用了一个网络，该网络将单个代理值的复杂非线性组合作为联合动作值进行估计，而每个代理值仅根据本地观测得到。我们在结构上强制每个代理的联合动作值是单调的，这使得在非策略学习中联合动作值的最大化能够实现，并保证了集中化和去中心化策略之间的一致性。我们在一组极具挑战性的星际争霸2微管理任务中对QMIX进行了评估，结果表明QMIX显著优于现有的基于价值的多智能体强化学习方法。

3. 论文主要观点：

3.1 背景：

强化学习在解决多代理协作问题如机器人群和自动驾驶汽车上有很大的潜力。在这种环境下，局部可观测性和通信限制使学习一个去中心化的策略成为必须，代理只根据本地观测历史进行决策。去中心化的的策略也减弱了联合动作空间随代理数量成指数增长的问题，这个问题使得传统的单代理RL方法无法应用到多代理场景中。幸运的是，去中心化的策略通常可以在仿真或实验室环境中以集中的方式学习。从而代理能够访问更多的状态信息，并移除了代理间的通信限制。集中训练分散执行的方式(Oliehoek et al., 2008; Kraemer & Banerjee, 2016)在强化学习领域中获得了更多的关注(Jorge et al., 2016; Foerster et al., 2018)。然而，关于如何最好地利用集中训练的许多挑战仍然存在。

这些挑战之一是如何表示和使用大多数RL方法学习的动作值函数。获得一个有效的代理动作决策需要一个基于全局状态和联合动作的中心动作价值函数$Q_{tot}$。另一方面，当有许多代理时，这样的函数很难学习，而且即使可以学习，也没有明显的方法来提取分散的策略，从而基于这些策略能够允许每个代理仅根据独立的观测选择独立的动作。

最简单的方法是使每个代理学习一个单独的动作价值函数$Q_a$，例如Independent Q-learning (IQL) (Tan, 1993)。然而，这种方法不能明确地表示代理之间的交互，也可能不收敛，因为每个代理的学习都被其它代理的学习和探索干扰。

还有一种方法是学习一种完全集中化的状态动作价值函数$Q_{tot}$，使用这个价值函数来在actor-critic框架下生成一个去中心化的策略，例如Counterfactual multi-agent (COMA) policy gradients (Foerster et al., 2018)以及Gupta et al. (2017)。然而，这需要策略学习，而策略学习的样本效率可能很低，而且，当有多个代理时，训练完全集中的critic变得不切实际。

在这两个极端之间，我们可以学习一种集中化但经过分解的$Q_{tot}$，这是价值分解网络(VDN)采用的一种方法(Sunehag et al., 2017)。$Q_{tot}$为所有代理基于各自观测的价值函数$Q_a$的和，那么去中心化的策略就可以通过每个代理通过贪婪策略选择使它自己的价值函数最大化的动作$Q_a$。然而,VDN严重限制了可表示的集中化动作价值函数的复杂性，并且忽略了训练期间可用的任何额外状态信息。

3.2 问题：

Dec-POMDP问题的描述：

A fully cooperative multi-agent task can be described as a Dec-POMDP (Oliehoek & Amato, 2016) consisting of a tuple $G=<S,U,P,r,Z,O,n,\gamma >.s\in S$ describes the true state of the environment. At each time step, each agent $a\in A\equiv \{1,\dots ,n\}$ chooses an action $u^a\in U,$ forming a joint action $\mathbf{u}\in \mathbf{U}\equiv U^n.$ This causes a transition on the environment according to the state transition function $P\left(s^{\prime }|s,\mathbf{u}\right):S\times \mathbf{U}\times S\to [0,1].$ All agents share the same reward function $r(s,\mathbf{u}):S\times \mathbf{U}\to \mathbb{R}$ and $\gamma \in [0,1),$ where the $\gamma$ is a discount factor.

We consider a partially observable scenario in which each agent draws individual observations $z\in Z$ according to observation function $O(s,a):S\times A\to Z.$ Each agent has an action-observation history ${\tau }^a\in T\equiv (Z\times U{)}^{\ast },$ on which it conditions a stochastic policy ${\pi }^a\left(u^a|{\tau }^a\right):T\times U\to [0,1]$.

The optimisation objective is to maximise the discounted return: $R_t={\sum }_{l=0}^{\infty }{\gamma }^i{r}_{t+l}.$ The joint policy $\pi$ produces a joint action-value function:
$$Q^{\pi }\left(s_t,{\mathbf{u}}_t\right)={\mathbb{E}}_{s_{t+1:\infty ,{\mathbf{u}}_{t+1;\infty }}}\left[R_t|s_t,{\mathbf{u}}_t\right]$$
Although training is centralised, execution is decentralised, i.e., the learning algorithm has access to all local actionobservation histories $\tau$ and global state $s,$ but each agent’s learnt policy can condition only on its own actionobservation history ${\tau }^a$.

3.3 方法：

在本文中，我们提出了一种新的方法，称为QMIX，它与VDN一样，介于IQL和COMA之间，但可以表示更丰富的动作价值函数类。**我们的方法的关键是认识到VDN的完全分解对于提取分散的策略是不必要的。**相反，我们只需要确保在$Q_{tot}$上执行的全局argmax与在每个$Q_a$上执行的单个argmax操作集产生相同的结果。
$$\underset{\mathbf{u}}{\mathrm{argmax}}{Q}_{tot}=\left(\begin{array}{c}\arg {\max }_{u^1}{Q}_1\\ \cdots \\ \arg {\max }_{u^n}{Q}_n\end{array}\right)$$
这样，每个代理就可以通过贪婪策略选择动作$a$来使$Q_a$最大化，来参与到分散决策的过程中。VDN的表示足以满足上式，然而，QMIX基于这样的观察：这种表示可以推广到更大的单调函数族，这些单调函数族对于满足上式也是充分的，但不是必需的。

为此，我们可以通过对$Q_{tot}$和每个$Q_a$之间的关系进行约束来满足单调性：
$$\frac{\partial Q_{tot}}{\partial Q_a}\ge 0,\forall a\in A.$$
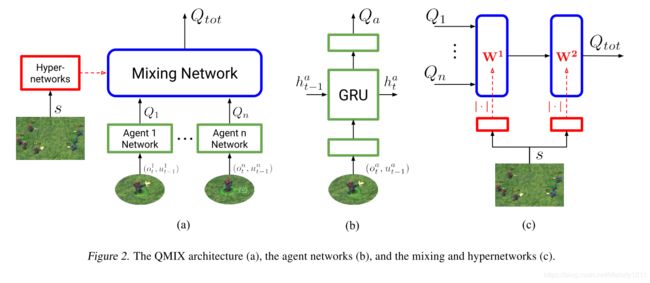
为了实现上式，QMIX使用由代理网络、混合网络和一组超网络组成的体系结构表示$Q_{tot}$。如下图：

对于每一个代理$a$都有一个代理网络表示独立的价值函数$Q_a({\tau }^a,u^a)$。将代理网络表示为DRQNs，在每个时间步，接收当前的独立观察$o_a^t$和最后的动作$u_{t-1}^a$作为输入。并且在代理网络之间应用了权值共享。为了是不同的代理执行不同的动作，代理的IDs被包括在了观测之中。

混合网络是以代理网络输出为输入，进行单调混合，得到$Q_{tot}$值的前馈神经网络。限制权重为正值以保证满足单调性约束。这使得混合网络可以任意接近任何单调函数。

每个超网络以全局状态$s$的形式作为输入获取额外的状态信息，并生成混合网络一层的权值。每个超网络都是一个单一的线性层，然后是一个取超网络输出绝对值的激活函数，以确保混合网络的权值是非负的。请注意，全局状态由超网络使用，而不是直接传递到混合网络。这是因为$Q_{tot}$允许以非单调的方式依赖于额外的状态信息，所以将$s$的一些函数与每个代理的值一起通过单调网络传递会受到过度的约束。相反，超网络的使用使得以任意方式调整单调网络在s上的权值成为可能，从而尽可能灵活地将完整状态s集成到联合动作价值估计中。

QMIX通过端到端的训练以最小化以下损失：
$$\mathcal{L}(\theta )=\sum _{i=1}^b\left[{\left(y_i^{\text{tot }}-Q_{\text{tot }}(\mathbf{\tau },\mathbf{u},s;\theta )\right)}^2\right]$$
where $b$ is the batch size of transitions sampled from the replay buffer, $y^{\text{tot }}=r+\gamma {\max }_{{\mathbf{u}}^{\prime }}{Q}_{\text{tot}}\left({\mathbf{\tau }}^{\prime },{\mathbf{u}}^{\prime },s^{\prime };{\theta }^{-}\right)$ and${\theta }^{-}$ are the parameters of a target network as in DQN. (6) is analogous to the standard DQN loss of (2). since (4) holds, we can perform the maximisation of $Q_{tot}$ in time linear in the number of agents (as opposed to scaling exponentially in the worst case).

QMIX由代表每个$Q_a$的代理网络和将它们组合成$Q_{tot}$的混合网络组成，而不是像VDN中的简单和，而是以复杂的非线性方式确保集中化和分散化策略之间的一致性。同时，通过限制混合网络的权值为正来实现上式的约束。因此，QMIX可以用一个因子表示来表示复杂的集中化的动作值函数，这个因子表示可以很好地扩展代理的数量，并且允许通过线性时间的单个argmax操作轻松地提取分散的策略。

QMIX在绝对性能和学习速度方面都优于IQL和VDN。特别是，我们的方法在具有异构代理的任务上显示了可观的性能收益。此外，文中的分析表明，为了实现任务间的一致性能，必须对状态信息进行调节，并对代理Q值进行非线性混合。

3.4 结论：

这篇文章提出了QMIX算法——一个深度多代理强化学习算法，能够通过集中端到端的训练学习到分散策略，并且有效的利用了额外了状态信息。QMIX能够学习到丰富的联合动作价值函数，这确保了价值函数能够分解为每个代理的价值函数。这是通过对混合网络施加单调性约束实现的。

在多代理强化学习中，存在代理单独计算价值函数和完全集中计算价值函数两种方式，前者存在不稳定的问题，后者存在可扩展性差的问题（维度灾难）。作者在介于两者之前的VDN算法的基础上，对从单代理价值函数到中心价值函数之间的映射关系进行了改进，在映射的过程中将原来的线性映射换为非线性映射，并通过超网络的引入将额外状态信息加入到决策过程，提高了模型性能。