方差分析以及如何用SPSS实现单因素、双因素方差分析

一、方差分析是什么？

方差分析（analysis of variance，ANOVA）是分析各类别变量（如区位）对数值变量（如销售额）的影响的一种统计方法。

二、方差分析的原理是什么？

方差分析是通过分析数据误差来检验类别变量对数值变量的影响是否显著。也就是说因变量的总误差中，除开随机误差以外，是否有类别变量（自变量）造成的处理误差，有多少误差是自变量造成的。

总误差=处理误差+随机误差

三、方差分析的分类

一个类别自变量→单因素方差分析

两个类别自变量：只考虑主效应，而不考虑交互效应→无重复双因素分析

                             考虑主效应，也考虑交互效应→可重复双因素分析

这里的交互效应是指，除开自变量对因变量单独造成的影响外，还有可能是自变量自己的组合也会对因变量造成影响。例如，自变量区位、竞争者数量都会对销售额造成影响，他们的交互影响就指的是不同的区位和竞争者数量组合也会对销售额造成影响。

在方差分析中，一个类别变量称为一个因素，一个类别变量可以有多种取值，比如区位可以区市区、郊区、农村，其取值就称为因素的处理（treatment)或者水平（level），即一个因素可能有多种处理。

 四、方差分析的条件

①独立性：要求每个样本数据来自不同处理的独立样本

②正态性：要求每个处理对应的总体都应该服从正态总体分布，检验方法有P-P图、Q-Q图、Shapiro-Wilk检验（适合3-50的小样本）、K-S检验

③方差齐性：各个处理的总体方差必须相等

检验方法：箱线图、残差图、Levene方差检验（原假设为各处理总体方差相等）

                tips：方差分析对 方差齐性要求实际较弱，略有不齐时，对分析的结果影响不是很大，尤其是当各处理的样本量相同时，方差分析对方差齐性时稳健的（robust）

五、方差分析操作示例：

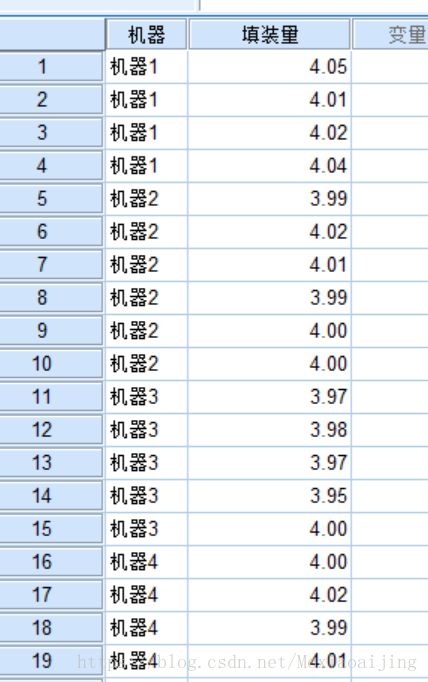
1.单因素方差分析：拿到不同机器牛奶装填量的数据，在α=0.05的显著性水平下，检验不同机器对装填量是否有显著性影响

分析：只有一个 类别变量（机器种类，其处理为1、2、3、4），故为单因素方差分析

设机器对装填量的影响效应分别为α1、α2、α3、α4，则提出的假设应该为：

Ho：α1=α2=α3=α4=0，（机器对装填量没有影响）、

H1：α1、α2、α3、α4至少有一个不等于0（机器种类对装填量有影响）

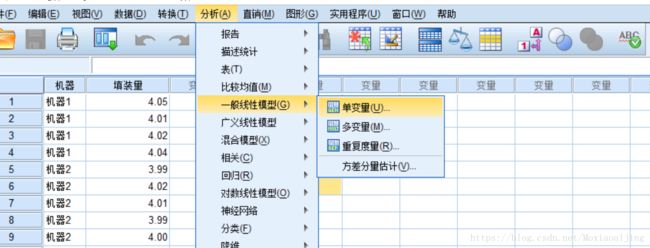
使用SPSS进行分析：①：分析→一般线性模型→单变量

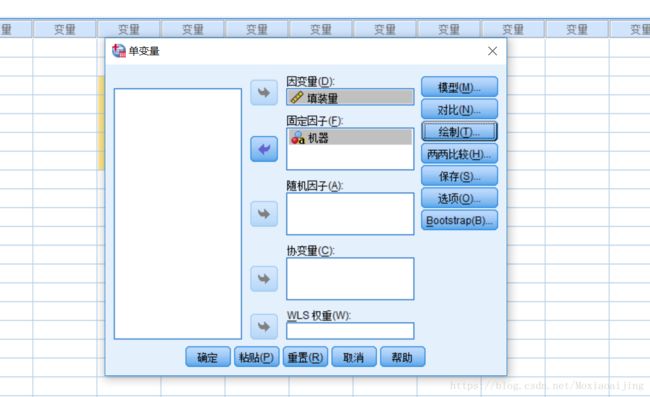
②：将因变量选入因变量，自变量选入固定因子，

③：需要均值图时，点击绘制，将因子（机器）选入水平轴，点击添加，点击继续回到主对话框

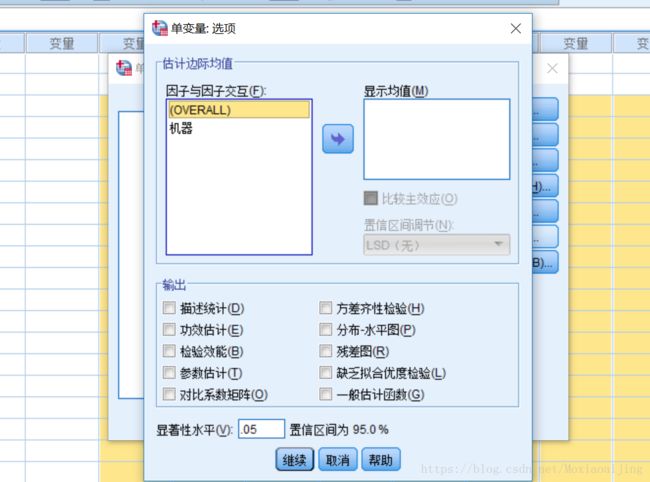
④：点击选项，出现如下所示

如果需要均值图，将自变量选入显示均值；

如果需要描述性统计，在输出框下勾选；

如果需要方差齐性检验、残差图、参数估计等多种输出，直接勾选即可。

这里我们勾选描述统计、方差齐性检验、残差图、参数估计。点击继续回到主对话框，点击确定查看输出

 

 可以看到机器对应的p值=0.001，故应该拒绝原假设，也就是说机器不同对装填量有影响，再看到R方0.669.这说明装填量误差有66.9%是由机器不同造成，剩余由随机误差造成。

2.多重比较：上述方差分析结果只告诉我们，机器种类的处理效应是显著的，但这一检验并未告诉我们究竟哪几种机器的装填量差额显著，因此需要进行多重比较，在单变量主对话框中，点击两两比较，将自变量选入两两比较对话框，

 我们看到有多种多重比较方法，常用的有两种:

LSD:Fisher的最小显著差异方法，适用于研究者事先就已经计划好要对某对或某几对均值进行比较，不管方差分析的结果如何都要进行比较

Turkey-Kramer的HSD方法：适用于研究者并未事先计划进行多重比较，只是在方差分析拒绝原假设后，才需要对任意两个处理的均值进行比较

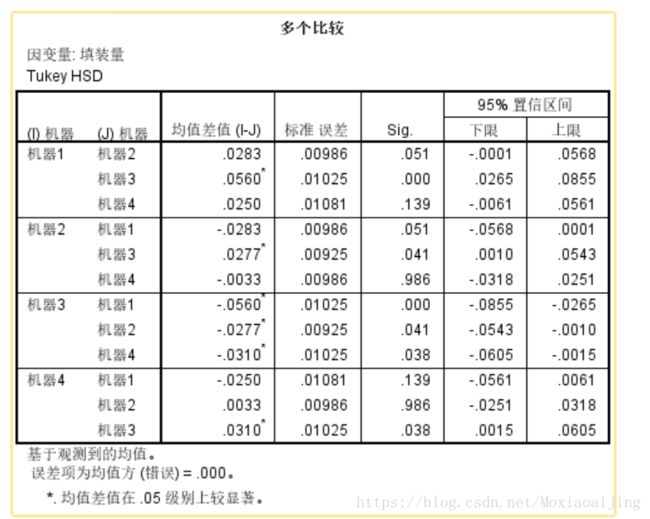
在这里我们选择Turkey的HSD方法，得到如下结果：

从结果可以看出，机器三和机器一差距显著。 

3.双因素方差分析：分为只检查主效应、不仅检查主效应还检查交互效应；

为研究不同路段和不同时间段对行车时间的影响，得到如下数据，并进行方差分析：

①分析→一般线性模型→单变量来到主对话框，

② 将因变量选入因变量框，自变量（两个）选入固定因子框，这里的操作类似于单因素方差分析，但是有几个区别需要注意：

点击模型→设定，将路段和时段两个自变量选入模型，注意：如果只检验主效应，在构建项的类型下选中主效应，然后就点击继续回到主对话框，如果还需要检验交互效应，就同时选中路段和时间段（用CTRL），将其同时选到模型，再在构建项的类型下选中交互效应，点击继续回到主对话框：图示如下：

  然后点击确定即可，将两种方式的输出结果图示如下：

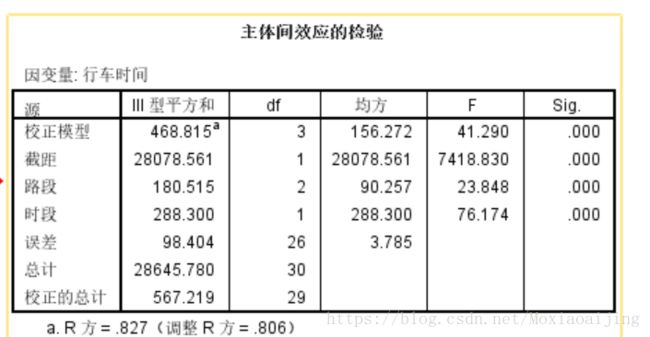
只检验主效应：可以看出没有交互项，给出了多重判定系数R方，说明路段和时段联合起来对行车时间误差的处理效应为82.7%，剩余的为随机误差。

检验主效应同时检验交互效应：可以看到多了一个交互项，但在这个题目里，交互项没有影响。

 

注意：SPSS中，可以实现方差分析的有两个地方，比较均值→单因素ANOVA，这里的单因素是指单一的自变量

而一般线性模型里的单变量指的是单一的因变量。