数学建模——图与网络（3）——最短路问题
文章目录
- 一、两个指定顶点之间的最短路径
- 1. 问题描述
- 2. 问题理解
- 3. 相关算法：迪克斯特拉（Dijkstra）算法
- 4. 示例问题
- 1. 绘制带权网络图：
- 方法1：[在线绘图](https://csacademy.com/app/graph_editor/)
- 方法2：使用Matlab绘图
- 1. 绘制带权网络图
一、两个指定顶点之间的最短路径
1. 问题描述
- 给出了一个连接若干个城镇的铁路网络，在这个网络的两个指定城镇间， 找一条最短铁路线。
2. 问题理解
- 以各城镇为图G的顶点，两城镇间的直通铁路为图G相应两顶点间的边，得图G；
- 对G的每一边e，赋以一个实数w(e) ——直通铁路的长度，称为e的权，得到赋权图G，G的子图的权是指子图的各边的权和。
- 到此，问题转化为 求赋权图G 中指定的两个顶点u0,v0间的最小权的轨。这条轨叫做u0,v0间的最短路，它的权叫做u0,v0间的距离，亦记作 d(u0,v0)。
3. 相关算法：迪克斯特拉（Dijkstra）算法
4. 示例问题
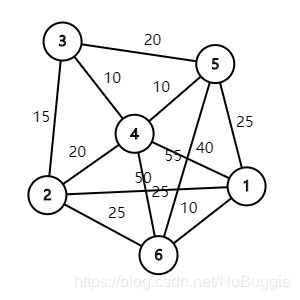
某公司在六个城市c1,c2,…,c6中有分公司，从ci到cj的直接航程票价记在下述矩阵的(i,j)位置上。（∞表示无直接航路），请帮助该公司设计一张城市c1到其它城市间的票价最便宜的路线图。
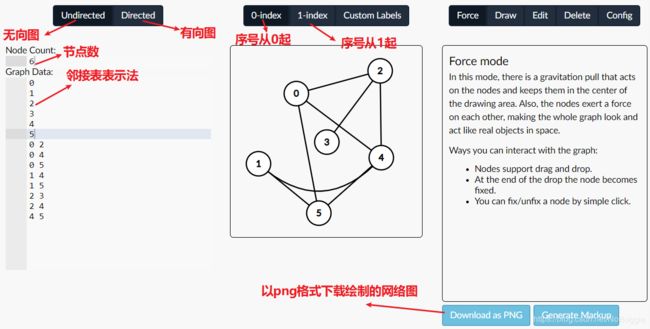
1. 绘制带权网络图：
方法1：在线绘图
使用该工具所制作的赋权无向图如下所示：
方法2：使用Matlab绘图
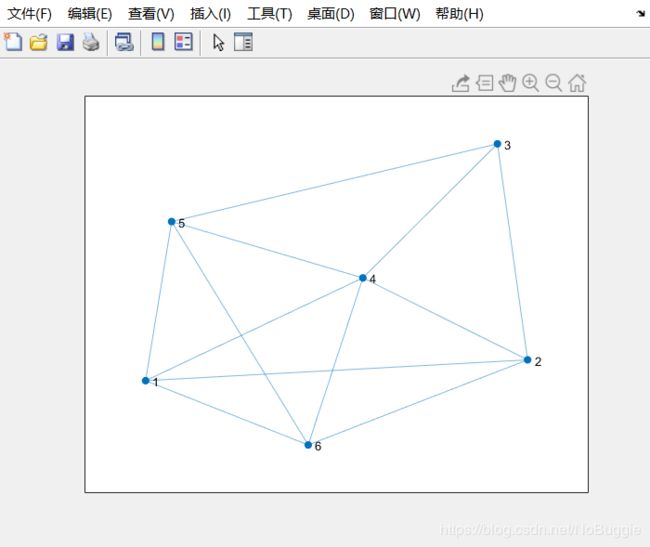
- 无权无向图
- 代码如下：
%% Matlab作无向图
%（1）无权重（每条边的权重默认为1）；
% 函数graph(s,t)：可在 s 和 t 中的对应节点之间创建边，并生成一个图；
% s 和 t 都必须具有相同的元素数；这些节点必须都是从1开始的正整数，或都是字符串元胞数组。
% 注意：编号应从1开始连续编号，注意：连续编号！（可以尝试一下不连续编号哦~）
s1 = [1,1,1,1,2,2,2,3,3,4,4,5];
t1 = [2,4,5,6,3,4,6,4,5,5,6,6];
G1 = graph(s1, t1);
plot(G1);
% plot(G1,'linewidth',2); %设置线的宽度
% set(gca,'XTick',[],'Ttick',[]); %绘图后不显示坐标
- 生成的无权无向图如下：
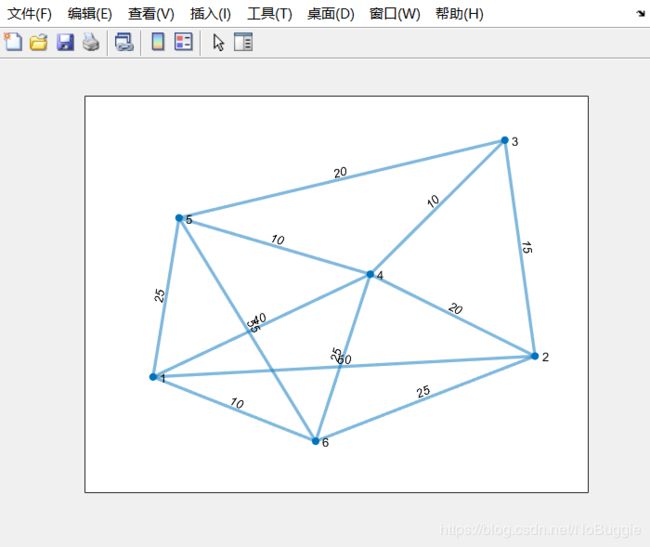
- 赋权无向图
- 代码如下：
%（2）有权重
% 函数graph(s,t,w)：可在 s 和 t 中的对应节点之间以w的权重创建边，并生成一个图
s2 = [1,1,1,1,2,2,2,3,3,4,4,5];
t2 = [2,4,5,6,3,4,6,4,5,5,6,6];
w = [50,40,25,10,15,20,25,10,20,10,25,55];
G2 = graph(s2, t2, w);
plot(G2, 'EdgeLabel', G2.Edges.Weight, 'linewidth', 2);
- 生成的赋权无向图如下：
1. 绘制带权网络图
求第一个城市到其它城市的最短路径的Matlab代码如下：