面试准备：逻辑智力题

1. 走最远

• 题目：
  一个车队有5辆同样的汽车，每辆车上装满的油能使汽车前进480千米，车子之间可以互相加油，现在5辆车同时出发，怎样安排能使其中一辆车走的最远，最远走多远？

如果只有两辆车：
假设行驶x里，首先x里必定要大于480km的一半才行，否则多余的油就浪费了。
行驶里程：$（480-x）\ast 2+x=960-x，x>=240$，故取$x=\frac{1}{2}$。
也就是是先行驶1/2后，再将剩余1/2的油输入给另一辆。

这道题隐藏的信息是：

1. 不能浪费多余的油。
2. 同时k辆车行驶，行驶距离越多，同时消耗的是k辆车的油。

所以要保证，不能浪费油的同时，k辆车行驶的距离越少。也就是慢慢减少车的并行数量。

所以，5辆车并行的时候，跑1/5的油，然后用4/5的油给其余4辆加满。
4辆车并行的时候，跑1/4的油，然后用3/4的油给其余3辆加满。
…

公式为：$480\ast (\frac{1}{5}+\frac{1}{4}+\frac{1}{3}+\frac{1}{2}+1)=1096$

• 题目：
  每个飞机只有一个油箱, 飞机之间可以相互加油(注意是相互,没有加油机) 一箱油可供一架飞机绕地球飞半圈,问题：为使至少一架飞机绕地球一圈回到起飞时的飞机场,至少需要出动几架飞机？(所有飞机从同一机场起飞,而且必须安全 返回机场,不允许中途降落,中间没有飞机场)

这道题，相当于前面车还需要返回了，所以算上返回，刚好用完一飞机的油最佳。并且刚好能让另一个飞机的油加满。
考虑如果有两个飞机，能飞多远？假设油箱飞行距离是单位1，地球一圈距离是单位2。
$1-2x=x$ 即 $x=\frac{1}{3}$ 所以，最终另一个飞机能飞1/3+1的单位。

现在的问题是出动几架飞机，假设k个飞机，那么：
$1-2x\ast (k-1)=(k-1)x$ 即 $x=\frac{1}{3(k-1)}$
并且，之后的情况相当于是k-1个飞机再飞，所以最终：
$\frac{1}{3(k-1)}+\frac{1}{3(k-2)}+\frac{1}{k-3}+....+\frac{1}{3}+1=2$
带入数据计算出$k=4$

但是这道题有个难点，如果我不是原路返回，由于地球是圆的，过了半程后，反方向飞更省，如果考虑这个上面的公式就不对了，但是由于是取整，所以答案还是对的。

• 题目：
  有一人有240公斤水，他想运往干旱地区赚钱。他每次最多携带60公斤，并且每前进一公里须耗水1公斤（均匀耗水）。假设水的价格在出发地为0，以后，与运输路程成正比，（即在10公里处为10元/公斤，在20公里处为20元/公斤…），又假设他必须安全返回，请问，他最多可赚多少钱？

很明显，每次拖最多的水60kg，跑4趟，那么每次跑到哪呢？
$y=x\ast (60-2x)=60x-2x^2$
求导可得$y^{’}=60-4x=0$，得$x=15$
所以在15km的时候取得最大值，即900-450=450
跑4趟，即4*450元

• 题目：
  一个商人骑一头驴要穿越1000公里长的沙漠,去卖3000根胡萝卜。已知驴一次性可驮 1000根胡萝卜,但每走一公里又要吃掉一根胡萝卜。问：商人共可卖出多少胡萝卜？

很明显这道题的逻辑和前面两个不同，因为一次性是无法穿越沙漠的（即使穿越了也不剩胡萝卜了），所以唯一可能的方法就是在中途卸下胡萝卜，采用接力的方式穿越沙漠，那么这个存档点的距离就需要计算。

显然每次回到原点都要拿1000根。
因为驴一次最多驮1000根，所以为了最大化，在第一次卸下萝卜的地点刚好使用1000根即可。设驴走X公里第一次卸下萝卜（3次都要经过x公里，其中前两次还有返回）：5x=1000，x=200

同理，第二次休息的地点也可以刚好使用1000:
3y=1000，y=333.3

而此时总共走了：200+333.3=533.3公里,而剩下的466.7公里只需要吃466根萝卜
所以可以卖萝卜的数量就是1000-466=534.

2. 最短时间过河

• 题目：
  过河一个晚上,四个人想要通过桥过河去,A通过桥最快要10分钟,B要5分钟,C要2分钟,D要1分钟,可是他们只有一个手电筒,每次最多只能有两个人一起过河,要在17分钟内过河,该怎么过呢?

这道题的隐藏信息是：

1. 需要让走的最快的人多走几次，走的慢的人少走几次（最好只走一次）。

故：
CD过河，D回来；AB过河，C回来；CD再次过河。
2+1+10+2+2=17分钟。

3. 烧绳子

• 题目：
  （1）烧一根不均匀的绳要用一个小时，如何用它来判断半个小时？
  （2）烧一根不均匀的绳，从头烧到尾总共需要1个小时。现在有若干条材质相同的绳子，问如何用烧绳的方法来计时四十五分钟？如何计时一个小时十五分钟呢?

这道题突破口是绳子应该怎么使用，要知道如果单纯用来烧，是无法产生差额的，那么怎么才能产生差额呢？两边同时烧。

我们来看现在能产生的数据：

1. 烧一根绳：60min
2. 绳子两端同时烧：30min

产生了30分钟的差额，也就是：两根绳子，一根烧一端，另一根烧两端，能计时30分钟。

那么十五分钟怎么产生了？很明显30分钟的差额能够再次对半：

1. 两根绳子，一根烧一端，另一根烧两端，当两端绳子烧完时，一端绳还剩30分钟才能烧完。这时，时间过去了30分钟。
2. 剩下30分钟能烧完的绳子，现在烧两端，15分钟就能烧完。这时时间过去了45分钟。
3. 再取一根绳子，烧两端，烧完时，时间过去了1小时15分钟。

4. 谁养鱼

• 题目：
  前提：
  1、有五栋五种颜色的房子
  2、每一位房子的主人国籍都不同
  3、这五个人每人只喝一种饮料，只抽一种牌子的香烟，只养一种宠物
  4、没有人有相同的宠物，抽相同牌子的香烟，喝相同的饮料
  提示：
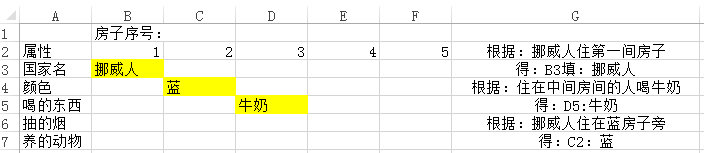
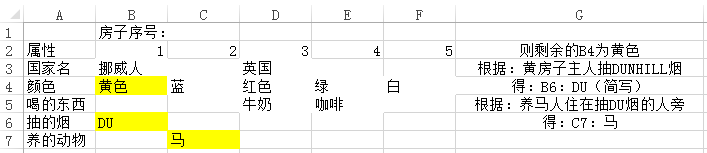
  1、英国人住在红房子里
  2、瑞典人养了一条狗
  3、丹麦人喝茶
  4、绿房子在白房子左边
  5、绿房子主人喝咖啡
  6、抽ＰＡＬＬ ＭＡＬＬ烟的人养了一只鸟
  7、黄房子主人抽ＤＵＮＨＩＬＬ烟
  8、住在中间那间房子的人喝牛奶
  9、挪威人住第一间房子
  10、抽混合烟的人住在养猫人的旁边
  11、养马人住在抽ＤＵＮＨＩＬＬ烟的人旁边
  12、抽ＢＬＵＥ　ＭＡＳＴＥＲ烟的人喝啤酒
  13、德国人抽ＰＲＩＮＣＥ烟
  14、挪威人住在蓝房子旁边
  15、抽混合烟的人的邻居喝矿泉水
  问题是：谁养鱼？

这道题，把表列出来即可：

5. 猜牌

• 题目：
  A 先生、B先生、C先生他们知道桌子的抽屉里有16张扑克牌：
  红桃A、Q、4
  黑桃J、8、4、2、7、3
  草花K、Q、5、4、6
  方块A、5
  test教授从这16张牌中挑出一张牌来，并把这张牌的点数告诉B 先生，把这张牌的花色告诉C先生。这时，test教授问B先生和C先生：你们能从已知的点数或花色中推知这张牌是什么牌吗？ 于是，A先生听到如下的对话：
  1⃣️B先生：我不知道这张牌。
  2⃣️C先生：我知道你不知道这张牌。
  3⃣️B先生：现在我知道这张牌了。
  4⃣️C先生：我也知道了。
  听罢以上的对话，A先生想了一想之后，就正确地推出这张牌是什么牌。
  请问：这张牌是什么牌？

我们来分析第一轮对话：
1⃣️B先生：我不知道这张牌。
B首先知道了点数，光凭借点数不能知道这是什么牌，那么具有重复点数的是：A\Q\4\5

2⃣️C先生：我知道你不知道这张牌。
考虑一下，C能够明确的说出B不知道这张牌，说明了B 一定不会拿到A\Q\4\5之外的点数，否则B 可能是会知道是哪张牌的。所以那个花色一定不会包含A\Q\4\5以外的花色：
红桃\方块

我们总结一下现在B和C能得到的信息：

• A\Q\4\5
• 红桃\方块

我们接着分析第二轮对话：

3⃣️B先生：现在我知道这张牌了。
现在B说，能知道这张牌，那么一定是在上面两个信息中没有重叠的牌，由于红桃A和方块A是重叠的，B能知道是哪张牌，那么一定不是这两张牌。
方块 ：-A- 、5
红桃 ：-A- 、Q、4

4⃣️C先生：我也知道了。
现在C能得到的信息增加了一项，能够排除方块A。而C 明确的 说知道了，那么只能是方块5了。不然红桃有两个选项是不能够明确的知道是哪张的。

6. 量筒倒水

• 题目
  假设有一个池塘，里面有无穷多的水。现有2个空水壶，容积分别为5升和6升。问题是如何只用这2个水壶从池塘里取得3升的水。

很明显，这种题也是凑差额。
我们来看5升壶和6升壶能够凑出哪些差额？

• 装满6升，倒入5升，还剩1升。
• 再次装满6升，倒入5升，还剩2升。
• 再次装满6升，倒入5升，还剩3升，

一不小心就凑出来了。

另外其他还可以凑其他数字：

• 装满5升，倒入6升，6升还有1升的空间。
• 再次装满5升，倒入6升，5升还有4升的水。（然后清空6升，将4升水装入6升）
• 再次装满5升，倒入6升，5升还有3升水。

另一种方法也能凑出3升水来。

• 题目
  有三个桶,两个大的可装8斤的水,一个小的可装3斤的水,现在有16斤水装满了两大桶就是8斤的桶,小桶空着,如何把这16斤水分给4个人,每人4斤。没有其他任何工具, 4人自备容器,分出去的水不可再要回来。

也是找差额，与前面的题不同的是：只有16斤水，不能浪费。
（8，5，3）->（8，5，0）：3斤清空给一个人(A:3)。
（8，5，0）->（8，2，3）->（8，0，3）->（8，3，0）：2斤清空给一个人(B:2)。
（8，3，0）->（5，3，3）->（5，6，0）->（2，6，3）->（2，8，1）->（2，8，0）：1斤清空给C(C:1)。
（2，8，0）->（2，5，3）->（7，0，3）->（7，3，0）->（4，3，3）->（4，6，0）->（1，6，3）->（1，8，1）->（1，8，0）：1斤清空给A（A:4）
（1，8，0）->（1，5，3）->（4，5，0）->（4，2，3）->（0，0，0）：2斤给B（B:4），3斤给C(C:4)，4斤给D（D:4）
结束。

• 题目
  据说有人给酒肆的老板娘出了一个难题：此人明明知道店里只有两个舀酒的勺子, 分别能舀7两和11两酒,却硬要老板娘卖给他2两酒。聪明的老板娘毫不含糊,用这两个勺子在酒缸里舀酒,并倒来倒去,居然量出了2两酒,聪明的你能做到吗？

找差额：
方法一：
(0,0)->(11,0)->(4,7)->(4,0)->(0,4)->(11,4)->(8,7)->(8,0)->(1,7)
量出1两，先给他，然后重复这个步骤再量出1两
方法二：
(0,0)->(0,7)->(7,0)->(7,7)->(11,3)->(0,3)->(3,0)->(3,7)->(10,0)->(10,7)->(11,6)->(0,6)->(6,0)->(6,7)->(11,2)
直接给2两酒。

7. 三个火枪手

• 题目：
  三个小伙子同时爱上了一个姑娘，为了决定他们谁能娶这个姑娘，他们决定用枪进行一次决斗。小李的命中率是30％，小黄比他好些，命中率是50％，最出色的枪手是小林，他从不失误，命中率是100％。由于这个显而易见的事实，为公平起见，他们决定按这样的顺序：小李先开枪，小黄第二，小林最后。然后这样循环，直到他们只剩下一个人。那么这三个人中谁活下来的机会最大呢？他们都应该采取什么样的策略？

首先，为了简单讨论，把三个人分别教程30、50、100。

1. 而最好推测的是100，因为对他威胁最大的是50，所以他会优先杀50.
2. 现在50知道了100会优先杀他，他也会优先杀100，这是毋庸置疑的。

最麻烦的在于30，30 最希望看到的结果是：50杀了100，而自己杀了50。因为万一自己第一枪打死了50，那么100会百分百杀死自己。
所以现在，30的第一枪，有三个选择：

1. 向50开枪
2. 向100开枪
3. 开空枪

我们分情况讨论：
第一次向50开枪，那么最终30自己活下来的过程为：

• 情况一：
  第一轮：30向50开枪，50没死；50向100开枪，100死了。
  第二轮：30和50单独pk。
• 情况二：
  第一轮：30向50开枪，50没死；50向100开枪，100没死；100向50开枪，50死了。
  第二轮：30向100开枪，100死了。

我们可以看到，第一次无论如何50不能死，所以，选择不向50开枪才是概率最大的。

第一次向100开枪，那么最终30自己活下来的过程为：

• 情况一：
  第一轮：30向100开枪，100死了；50向30开枪，30没死。
  第二轮：30和50单独pk。
• 情况二：
  第一轮：30向100开枪，100没死；50向100开枪，100死了。
  第二轮：30和50单独pk。
• 情况三：
  第一轮：30向100开枪，100没死；50向100开枪，100没死；100向50开枪，50死了。
  第二轮：30向100开枪，100死了。

第一次空枪，那么最终30自己活下来的过程为：

• 情况一：
  第一轮：50向100开枪，100死了。
  第二轮：30和50单独pk。
• 情况二：
  第一轮：50向100开枪，100没死；100向50开枪，50死了。
  第二轮：30向100开枪，100死了。

感性的分析：
如果30向100开枪，100死了，那么50会增加一次杀死自己的机会。
而如果100没死，和开空枪的情况一样。

所以最好的办法是，30在第一次放空枪。
情况一的概率：$50\%\ast （30\%+70\%\ast 50\%\ast 30\%+（70\%\ast 50\%{）}^2\ast 30\%+....+（70\%\ast 50\%{）}^n\ast 30\%）=50\%\ast li{m}_{n->\infty }\frac{30\%\ast (1-35{\%}^n)}{1-35\%}=23.08\%$，

等比数列求和公式：$S_n=\frac{a_1(1-q^n)}{1-q}$

情况二的概率：$50\%\ast 30\%=15\%$

故总的存活概率是：$38.08\%$。

8. 囚犯分汤

• 题目：
  一间囚房里关押着两个犯人。每天监狱都会为这间囚房提供一罐汤，让这两个犯人自己来分。起初，这两个人经常会发生争执，因为他们总是有人认为对方的汤比自己的多。后来他们找到了一个两全其美的办法：一个人分汤，让另一个人先选。于是争端就这么解决了。可是，现在这间囚房里又加进来一个新犯人，现在是三个人来分汤。必须寻找一个新的方法来维持他们之间的和平。该怎么办呢？

由其中一个人分汤，另两个犯人挑选他们认为最多的一碗，剩下的一碗留给分汤的那个人；然后把另两个犯人挑选的两碗汤混合在一起，再按两个人分汤的步骤分汤。

9. 硬币覆盖桌面

• 题目：
  在一张长方形的桌面上放了n个一样大小的圆形硬币。这些硬币中可能有一些不完全在桌面内，也可能有一些彼此重叠；当再多放一个硬币而它的圆心在桌面内时，新放的硬币便必定与原先某些硬币重叠。请证明整个桌面可以用4n个硬币完全覆盖。

一个隐藏的条件是：

• 每个硬币圆心之间的距离必然是小于单位2的。（假设硬币半径是单位1。所用条件：当再多放一个硬币而它的圆心在桌面内时，新放的硬币便必定与原先某些硬币重叠。）

利用这个条件，我们可以知道，整个桌面可以被n个半径为单位2的硬币覆盖。假如此时把桌面和硬币的尺度都缩小一倍，那么，长、宽各是原桌面一半的小桌面（面积就是原来的1/4），就可以用n个半径为1的硬币覆盖。

所以这就相当于把原来的桌子分割成相等的4块小容桌子，那么每块小桌子都可以用n个半径为1的硬币覆盖，因此，整个桌面就可以用4n个半径为1的硬币覆盖。

10. 猜数字

• 题目：
  一个教授逻辑学的教授，有三个学生，而且三个学生均非常聪明！一天教授给他们出了一个题，教授在每个人脑门上贴了一张纸条并告诉他们，每个人的纸条上都写了一个正整数，且某两个数的和等于第三个！（每个人可以看见另两个数，但看不见自己的）教授问第一个学生：你能猜出自己的数吗？回答：不能，问第二个，不能，第三个，不能，再问第一个，不能，第二个，不能，第三个：我猜出来了，是144！教授很满意的笑了。请问您能猜出另外两个人的数吗？

这道题的隐藏信息：

• 0不是正整数。 很隐晦的信息。

这道题，也是分轮次分析：
第一轮：三个人都回答不能
根据三个人都回答的不能，说明了没有重复数字，因为如果存在重复数组，比如A：5，B：5，那么由于纸上写的正整数，是大于0的，所以C就能明确知道自己的数字。

第二轮：三个人都回答不能
现在没有两个相同的数字了，三个人仍然回答不能，这次回答能够排除掉某一个数是另一个数的两倍大，比如A：5，B：10，C知道现在没有两个相同的数字，那么C不可能是5，C只能是15。

第三轮：AB都说不能，C回答144
现在，我们能得到的信息是自己拿到的数字要么是其余两数的和，要么是其余两数的差，而C能回答自己的数字，必然是排除了一种情况。

什么情况才能说明C排除了一种情况了，也就是C在第二轮得到了信息：没有一个数字是另一个数的两倍大。说明了C的一个情况里（和或者差），自己的数是某一个人的数的两倍大。

假设C的推测错误数字是A的两倍大：

• 假设推测的错误数字是两个数的和，A+B=2A，而C正确的数字是通过A-B=144得来的。得到C=0矛盾。
• 假设推测的错误数字是两个数的差，B-A=2A（不可能是A-B=2A，因为没有负数），而C的正确数字则是通过A+B=144得来的。得到A=36，B=72。

11. 马的数目

• 题目：
  现在共有100匹马跟100块石头，马分3种，大型马；中型马跟小型马。其中一匹大马一次可以驮3块石头，中型马可以驮2块，而小型马2头可以驮一块石头。问需要多少匹大马，中型马跟小型马？（必须是刚好用完100匹马）

列方程：
$x+y+z=100$
$3x+2y+z/2=100$

可得：$5x+3y=100$
由于x和y都是整数，那么y必然是5的倍数，如0,5,10,…

12. 排队方式

• 题目：
  有2n个人排队进电影院，票价是50美分。在这2n个人当中，其中n个人只有50美分，另外n个人有1美元（纸票子）。愚蠢的电影院开始卖票时1分钱也没有。问：有多少种排队方法使得每当一个拥有1美元买票时，电影院都有50美分找？

答案：$\frac{(2n)!}{2}$
因为50美分和1美元的人数是一样的，全排列之后如果某个排队方法找不开，整个队伍掉个头就肯定找的开，然后就会和找的开的一种排队方法重复，所以全排列除以2。

13. 运动分数

• 题目：
  有一种体育竞赛共含M个项目，有运动员A，B，C参加，在每一项目中，第一,第二,第三名分别的X，Y，Z分，其中X,Y,Z为正整数且X>Y>Z。最后A得22分，B与C均得9分，B在百米赛中取得第一。求M的值，并问在跳高中谁得第二名。

三人总得分：22+9*2=40分。
而得分是正整数，那么至少是1，2，3分及以上，那么比一次最少会有6分进账。但是6分除不清，那么至少得是8分，10分（不可能是40分，也不可能是20分如果只有两次比赛，那么B与A的数据应该是接近的）。

8分的组成有：（1，2，5），（1，3，4）
10分的组成有：（1，2，7），（1，3，6），（1，4，5），（2，3，5）

考虑10分组成，要比4次：

• （1，2，7）：如果得一次第一能有7分，那么B即使其他三场都拿最后一名，即7+1+1+1>9；
• （1，3，6）：B的构成6+1+1+1=9，那么C怎么构成呢：如果得第二名配不平（3+3+?+?=9），如果得第一名，没有那么多第三名了。
• （1，4，5）：B的构成：5+1+1+？=9 配不平。
• （2，3，5）：B也配不平。

所以考虑8分构成，要比5次：

• （1，3，4）：B的构成：4+3+? 配不平 或者 4+1+1+1+? 配不平。
• （1，2，5）：B的构成9=5+1+1+1+1。A的构成：5+5+5+5+2，C的构成：2+2+2+2+1。

所以M=5，跳高比赛第二名是B。

14. 称重

• 题目：
  有7克、2克砝码各一个，天平一只，如何只用这些物品三次将140克的盐分成50、90克各一份？

找差额：
7+2=9；9+9=18； 距离140克太远了。
7-2=5；5+5=10；同样也很远。

隐藏物品：140g盐，它可以自身对半分。
所以可以找到：
140=70+70；70=35+35；（现在，有两堆35g，一堆70g）
使用其中一堆35g的盐，现在需要找出15g和20g的分量（15+35，20+70），所以利用砝码：
15g+7g=20g+2g
就称出来了。

• 题目：
  12个球一个天平，现知道只有一个和其它的重量不同，问怎样称才能用三次就找到那个球。13个呢？（注意此题并未说明那个球的重量是轻是重）

很直接的想法就是先让12个球分成3组：ABC
第一次： 如果AB重量相同，就在C中（4个），否则在AB中（8个）。
第二次： 直接考虑在AB中的情况，8个也分3组，3+3+2，最坏情况是只能排除2个，还剩6个。
第三次：6个怎么分也不能找出那一个。
所以这种直接想法是不对的。

我们此时会察觉到，C中的（4个）必然是正确的重量！
第二次我们可以直接排除一半。
第二次：8个分2组：DE，D与C比较，不是D就是E，而且可以知道是重了还是轻了。
第三次：4个怎么分也没法找出哪一个（最多只能排除2个）。

说明了，第二次至少要排除到3个才行。那么第二次怎么才能排除到3个呢？现在的信息是：错误的球在这8个球里面，并且已知了4个正确重量的球。由于8个分3组的情况我们已经考虑过了，一定还有什么隐藏信息或者方法： 那就是球的轻重。
第一次：12个球分成3组，（A：1⃣️2⃣️3⃣️4⃣️）（B：5⃣️6⃣️7⃣️8⃣️）（C：9⃣️11，12）。A与B比较，如果A>B，说明要么是坏球是重的，在A里面；要么坏球是轻的，在B里面。
第二次：8个分成三组，（D：1⃣️2⃣️5⃣️）（E：3⃣️4⃣️6⃣️）(F：7⃣️8⃣️)。把D与E比较，如果D=E，说明坏球在7⃣️8⃣️里，和好球比较一次即可；如果DE，说明要么坏球是重的，是1⃣️2⃣️，要么坏球是轻的是5⃣️。
第三次：现在已经将球缩减到了2+1的模式，直接对比2个的那组就行。

15. 检验毒药

• 题目：
  1000瓶药水，1瓶有毒药，服用后一小时毒发，毒药可以无限稀释，那么一小时内用几只小白鼠能够找出毒药？

假如是8瓶药水，3只小白鼠。
000=0
001=1
010=2
011=3
100=4
101=5
110=6
111=7

每位数表示一只老鼠，0-7表示8个瓶子。即将1，3，5，7号瓶子的药混合取样给鼠1吃，2，3，6，7号瓶子混合取样给老鼠2吃……死鼠相应的位标为1。如鼠1死了，鼠2没死，鼠3死了，那么就是101=5号瓶子有毒。N只老鼠的量程为$2^N$，1000只瓶子位于$2^9$ ~ $2^{10}$，即10只小鼠可以测1000瓶水。

• 题目：
  10箱黄金,每箱100块,每块一两。有贪官,把某一箱的每块都磨去一钱 。请称一次找到不足量的那个箱子 。

1、10个箱子编上号，分别为1～10号。

2、1号箱取一块，2号箱取2块，3号箱取3块，依此类推……

3、共取出55块黄金，放在一起称量一次，正常情况下应该是55两。如果少一钱，说明贪的是1号箱，如果少两钱，说明贪的是2号箱，如果少三钱，说明贪的是3号箱,依此类推……

• 题目：
  有十瓶药,每瓶里都装有100片药,其中有八瓶里的药每片重10克,另有两瓶里的药每片重9克。用 一个精确的小秤,只称一次,如何找出份量较轻的那两个药瓶？

解法和上面相同。

16. 芯片比较

• 题目：
  芯片测试：有2k块芯片，已知好芯片比坏芯片多．请设计算法从其中找出一片 好芯片，说明你所用的比较次数上限． 其中：好芯片和其它芯片比较时，能正确给出另一块芯片是好还是坏． 坏芯片和其它芯片比较时，会随机的给出好或是坏。

把第一块芯片与其它逐一对比，看看其它芯片对度第一块芯片给出的是好是坏，如果给出是好的过半，知那么说明这是好芯片。
如果给出的是坏的过半，说明第一块芯片是坏的，那么就要在那些在给出第一块芯片内是坏的芯片中，重复上述步骤，直到找容到好的芯片为止。
方法复杂度（最坏情况，过半可以直接停止，所以第一次比较只需要n/2+1次）O(n/2+n/4+n/8+…+1)=O(n^2)，（最好情况）O(n/2+1)。

17. 钟表

• 题目：
  从前有一位老钟表匠, 为一个教堂装一只大钟。他年老眼花,把长短针装配错了, 短针走的速度反而是长针的12倍。装配的时候是上午6点,他把短针指在“6 ”上,长针指
  在“12”上。老钟表匠装好就回家去了。人们看这钟一会儿7点,过了不一会儿就8点了, 都很奇怪,立刻去找老钟表匠。等老钟表匠赶到,已经是 下午7点多钟。他掏出怀表来一
  对,钟准确无误,疑心人们有意捉弄他,一生气就回去了。这钟还是8点、9点地跑,人们 再去找钟表匠。老钟表匠第二天早晨8点 多赶来用表一对,仍旧准确无误。 请你想一想,
  老钟表匠第一次对表的时候是7点几分？第二次对表又是8点几分？

在6点,两针成为一直线,这是老钟表匠装配的时间。以后再做。

18. 海盗分金

• 题目：
  5名海盗抢得了窖藏的100块金子,并打算瓜分这些战利品。这是一些讲民主的海盗 (当然是他们自己特有的民主),他们的习惯是按下面的方式进行分配：最厉害的一名海盗提出分配方案,然后所有的海盗(包括提出方案者本人)就此方案进行表决。如果超过50%的海盗赞同此方案,此方案就获得通过并据此分配战利品。否则提出方案的海盗将被扔到海里,然后下一名 最厉害的海盗又重复上述过程。

5名海盗，分别是ABCDE。
对于E来说，无论如何他希望的都是前面的人都死掉，自己独吞100枚金币。
D了解到E的想法，所以如果最后只剩下D和E两个人，那么如果不给100枚金币给E，那么E会把他丢到海里。
C了解到DE的想法，所以，他无论提出什么方案，D都会接受，所以他会提出（100，0，0），投票比2：1。
B了解到CDE的想法，所以，他只要提出给D和E 1枚金币，那么D就会支持他的想法（98，0，1，1），投票比3:1
A了解到BCDE的想法，所以，他只要收买两个人即可，他可以（97，0，1，2，0），此时投票比3:2，注意，这里分给比原先多的金币才能稳稳的不被丢下海。

19. 存活几率

• 题目：
  5个囚犯,分别按1-5号在装有100颗绿豆的麻袋抓绿豆,规定每人至少抓一颗,而抓得最多 和最少的人将被处死,而且,他们之间不能交流,但在抓的时候,可以摸出剩下的豆子数。问他们中谁的存活几率最大？
  前提：
  1,他们都是很聪明的人　　　　　　
  2,他们的原则是先求保命,再去多杀人　　　　　　
  3,100颗不必都分完　　　　　　
  4,若有重复的情况,则也算最大或最小,一并处死

我们可以知道1号囚犯，无论摸多少颗，2号囚犯都能知道他摸了多少颗。3号囚犯能够知道1和2一共摸了多少颗，…。
另外，如果1号囚犯拿的太多，比如50颗，那么2号拿47颗，就能稳稳的保证自己不会死，并且还能害死1号和后面几号。所以1号囚犯不敢拿太多，他需要拿一个安全范围的豆子。

那么这个1号安全范围的豆子是多少呢？100/5=20，假如1号拿21颗，那么2号知道1号拿了21颗的情况下，如果自己拿了20颗，还剩59颗，3号也会拿41颗的平均20颗，因为必然有人比20颗要大，4号看到前面拿了61颗了，还剩39颗，如果自己拿20颗，必然也不是最小的，所以这种情况就是1、5会死。

所以1号不敢拿21颗，如果1号拿20颗呢？2号敢拿19颗吗？如果2号拿19颗，还剩61颗，如果后面的人都拿20颗和21颗，那么他也许会死。
所以2号也拿20颗，到了3号，他敢拿19颗吗？也不敢，3号也拿20颗，4号一看还剩40颗，如果自己拿19颗或者21颗，那么可能自己会成为最小的，5号一看还剩20颗，只能全拿，同归于尽。

同归于尽也许不是最好的选择，那么现在把1号的选择划分到2-19上来。这样我们打个比方选了个17吧。轮到2号选了，他如果犯错，选了不紧贴17的那个数（16或18），比如选个19，那么后面3个都会按平均数原理选择18，死的就是1号和2号，所以他犯错他自己必死，而且也把1号也给害了。

如果1号和2号都不犯错，1号选了20以下的数，2号选了紧贴1号的那个数，比他大1或者小1，那么3号犯错的情况下，比方说1号选了17，2号18，3号不犯错应该是17、18中任选一个，但他犯错了可能选了16或19，这时候1号或2号中有一个能活，而且活的概率是一样的。
综上三点，可见2号活的概率肯定比1号大，因为1号犯错2号能活，而2号犯错1号必死，且3号或3号以后犯错，1号和2号生存概率一样大。所以1号已经被KO了。接下来我们再看，1号犯错时，2号和3号都能活，2号犯错时3号能活，3号犯错时，2号只有一半概率活，而4号，5号犯错时，2号和3号生存概率一样。所以2号的存活率显然是不如3号的。同理可证，1号犯错时2号，3号，4号都能活，2号犯错时3号，4号都能活，3号犯错时4号能活，4号犯错时3号一半概率活，5号犯错时，3号和4号存活概率一样，所以3号存活概率不如4号。
最后5号非常特殊，1号犯错时，5号也必死，所以5号的存活概率肯定是不如4号的，综上，最终生存概率最高的一定是4号。

20. 谁是继承人

• 题目：
  说从前啊,有一个富 人,他有30个孩子,其中15个是已故的前妻所生,其余15个是继室所生,这后一个妇人很想让她自己所生的最年长的儿子继承财产,让我们把我们的30个孩子排成一个圆圈,从他们中的一个数起,每逢到10就让那个孩子站出去,直到最后剩下哪个孩子,哪个孩子就继承你的财产吧!"富人一想,我靠,这个题意相当有内涵了,不错,仿佛很公平,就这么办吧不过,当剔选过程不 断进行下去的时候,这个富人傻眼了,他发现前14个被剔除的孩子都是前妻生的,而且下一个要被剔除的还是前妻生的,富人马上大手一挥,停,现在从这个孩子 倒回去数, 继室,就是这个歹毒的后妈一想,倒数就倒数,我15个儿子还斗不过你一个啊。她立即同意了富人的动议,你猜,到底谁做了继承人呢？

21. 平分金条

• 题目：
  你让工人为你工作7天,给工人的回报是一根金条。金条平分成相连的7段,你必须 在每天结束时都付费,如果只许你两次把金条弄断,你如何给你的工人付费？

答案：
把金条标记分为长为1、2、4的三段，三段切两刀。
第一天给1。
第二天给2（让他还1）。
第三天给1。
第四天给4，让他还（1和2）。
…

22. 红眼难题

• 题目：
  一群人开舞会,每人头 上都戴着一顶帽子。帽子只有黑白两种,黑的至少有一顶。 每个人都能看到其它人帽子的颜色,却看不到自己的。主持人先让大家看看别人头上戴的 是什幺帽子,然 后关灯,如果有人认为自己戴的是黑帽子,就打自己一个耳光。第一次关 灯,没有声音。于是再开灯,大家再看一遍,关灯时仍然鸦雀无声。一直到第三次关灯, 才 有劈劈啪啪打耳光的声音响起。问有多少人戴着黑帽子？

略。

23. 猜帽子

• 题目：
  有3顶红帽子,2顶白帽子,现将其中的三顶给排成一列的三人每人戴一顶,每人却只能看到自己前面的人的帽子,而看不到自己和自己后面人的帽子,同时三人也都不知道剩下的两顶帽子的颜色（但却知道他们三人的帽子是三顶红帽子,两顶白帽子中取的）.
  先问站在最后边的人道：“你知道你戴的帽子是什么颜色的吗?”最后边的人回答说：“不知道.”接着让中间的人说出自己戴的帽子的颜色,中间的人回答说：“不知道”.听了他们两 人的回答后,你能知道站在最前面的人戴的是什么颜色的帽子吗?

最后一个人能看到2个帽子，如果他回答知道，那么前面的人必然是戴的2顶白帽子。所以现在前面的人要么是：1顶红帽+1顶白帽。要么是：2顶红帽。

再看第二个人，如果他回答知道，那么前面的人必然是戴的白帽子。现在他回答不知道，因为他不知道自己戴的是白帽子还是红帽子。

那么第一个人肯定能知道自己戴的红帽子。

• 题目：
  有3顶红帽子,4顶黑帽子,5顶白帽子。让10个人从矮到高站成一队,给他们每个人头上戴一顶帽子。每个人都看不见自己戴的帽子的颜色,却只能看见站在前面那些人的帽子颜色。 (所以最后一个人可以看见前面9个人头上帽子的颜色,而最前面那个人谁的帽子都看不见。现在从最后那个人开始,问他是不是知道自己戴的帽子颜色,如果他回答 说不知道,就继续问他前面那个人。最前面那个人一定会知道自己戴的是黑帽子。为什么？

太长略。

24. 拿到第N个球

• 题目：
  假设排列着100个乒乓球,由两个人轮流拿球装入口袋,能拿到第100个乒乓球的人为胜利者。条件是：每次拿球者至少要拿1个,但最多不能超过5个,问：如果你是最先拿球的人,你该拿几个？以后怎么拿就能保证你能得到第100个乒乓球？

考虑最简单的：
（1）假如球的个数小于6个，那么第一个人就能全拿完，第一个人必胜。
（2）假如球的个数刚好是6个，那么第二个人必胜。
（3）假如球的个数(6,11]，第一个人拿1-5个就能保证必胜。
（4）如果是12个，那么无论第一个人拿多少个，第二个人只需要拿到剩余6个，就可以回到情况（2），第二个人必胜。
（5）如果是(12,17]个，那么第一个人拿1-5个就能回到情况（3），第一个人必胜。

所以规律就出来了，只要球不是6的倍数，那么第一个人是必胜的，必胜方法就是第一次拿取1-5个，让球的个数刚好是6的倍数，然后之后无论第二个拿多少个，第一个人都将其凑到6个，也就是剩余的球是6的倍数，第一个人是稳赢的。
对于本题，就是一开始拿4个，凑到96个（6的16倍），然后无论第二个人拿1-5个，第一个人拿5-1个即可。

25.

其他题

• 题目：
  1
  1 1
  2 1
  1 2 1 1
  1 1 1 2 2 1
  下一行是什么？

第二行：一个1
第三行：两个1
第四行：一个2，一个1
…
故：3 1 2 2 1 1

• 题目：
  一个球、一把长度大约是球的直径2/3长度的直尺.你怎样测出球的半径？

1. 球放在平面上，尺子竖起来与球相切，切点就是球的半径。
2. 球放气，对折两次，直接量。

• 题目：
  五个大小相同的一元人民币硬币。要求两两相接触，应该怎么摆？

首先，一个平面显然是不可能的了。那么放到三维立体上来：

• 题目：
  某城市发生了一起汽车撞人逃跑事件，该城市只有两种颜色的车,蓝15%绿85%，事发时有一个人在现场看见了，他指证是蓝车，但是根据专家在现场分析,当时那种条件能看正确的可能性是80%那么,肇事的车是蓝车的概率到底是多少?

P=$\frac{15\%\ast 80\%}{15\%\ast 80\%+85\%+20\%}$

• 题目：
  一个家庭有两个小孩，其中有一个是女孩，问另一个也是女孩的概率?

P=$\frac{女女}{女男+男女+女女}=\frac{50\%\ast 50\%}{50\%\ast 50\%+50\%\ast 50\%+50\%\ast 50\%}=\frac{1}{3}$

• 题目：
  一楼到十楼的每层电梯门口都放着一颗钻石，钻石大小不一。你乘坐电梯从一楼到十楼，每层楼电梯门都会打开一次，只能拿一次钻石，问怎样才能拿到最大的一颗？

选择前五层楼都不拿，观察各层钻石的大小，做到心中有数。后五层楼再选择，选择大小接近前五层楼出现过最大钻石大小的钻石。

• 题目：
  为什么下水道的盖子是圆的？

1.面积小
2.圆心到边距离相等，不会掉。

• 题目：
  100个人回答五道试题，有81人答对第一题，91人答对第二题，85人答对第三题，79人答对第四题，74人答对第五题，答对三道题或三道题以上的人算及格， 那么，在这100人中，至少有（ ）人及格。

鸽巢原理，分别有19人，9人，15人、21人、26人错。要求至少多少人及格，反过来就是求最多有多少人错了三道。排序：9，15，19，21，26。
9，15，19，21，26
0，15，19，12，17 =》12，15，17，19=》 目前错三题9人。
0，15，5，7=》5，7，15-》目前错三题9+12人
0，2，13=》目前错三题：9+12+5人
故至少100-9-12-5=74人及格。好像和别人的答案不一样

转化为概率做：
第一道正确率：81%，依此类推：91%，85%，79%，74%，那么所求的是：全对+四个对+三个对。或者用100%减去一个错、两个错。
也就是$100\%-C_5^1(19\%+9\%+15\%+21\%+26\%)-C_5^2(19\%\ast 9\%+19\%\ast ...)$这样算的答案应该是对的。

• 题目：
  陈奕迅有首歌叫十年吕珊有首歌叫3650夜那现在问,十年可能有多少天?

这样可能包含1，2个闰年，3651或3652天。

• 题目：
  有一个大西瓜,用水果刀平整地切,总共切9刀,最多能切成多少份,最少能切成多少份?

在不移动西瓜的情况下，最少10，最多130。130=1 2 4 7 11 16 22 29 37，其中差额是1，2，3，4，5…

• 题目：
  假设现在有一个圆形的小岛，人在圆心，岛边上有一只鳄鱼想吃人，鳄鱼只能走圆的边缘，且鳄鱼游泳的速度是人走的四倍，人要怎么样走，才能比鳄鱼之前到达岛的边缘。

1.朝着鳄鱼反方向直接走，人的时间：r/v，鳄鱼时间：πr/4v，显然鳄鱼更快

2.走圆弧，不会算（把下面折线改成弧线）

3.走同心圆，算角速度，不会

• 题目：
  一天,harlan的 店里来了一位顾客,挑了25元的货,顾客拿出100元,harlan没零 钱找不开,就到隔壁飞白的店里把这100元换成零钱,回来给顾客找了75元零钱。 过一会 ,飞白来找harlan,说刚才的是假钱,harlan马上给飞白换了张真钱,问harlan赔了多少 钱？

75元+25元的货

• 题目：
  两个空心球,大小及重量相同,但材料不同。一个是金,一个是铅。空心球表面图 有相同颜色的油漆。现在要求在不破坏表面油漆的条件下用简易方法指出哪个是金的,哪个是铅的。

相同得力原地旋转两个球, 两球重心到内壁中心距离不同, 线速度不同.转得快得是金球.

• 题目：
  有23枚硬币在桌上,10枚正面朝上。假设别人蒙住你的眼睛,而你的手又摸不出硬币的 反正面。让你用最好的方法把这些硬币分成两堆,每堆正面朝上的硬币个数相同。

硬币分成两堆，一堆10枚，一堆13枚。
将10枚的那堆翻转。

• 题目：
  屋里三盏灯,屋外三个开关,一个开关仅控制一盏灯,屋外看不到屋里。怎样只进屋一次,就知道哪个开关控制哪盏灯? 四盏呢？

三个灯: 打开两个灯, 过一会关闭一个. 进去看亮着的, 不亮但是发热的,不亮也不发热的
四个灯: 打开两个灯, 过一会关闭一个, 然后打开一个新的灯, 不亮但是发热的, 亮但是
不发热的, 亮而且发热的, 不亮也不发热的.

• 题目：
  2+7-2+7全部有火柴根组成,移动其中任何一根,答案要求为30

将最后一个加号变成, 217, 将第一个加号变成247. 即247-217

• 题目：
  海滩上有一堆桃子，这是五个猴子的财产，它们要平均分配。第一个猴子来到海滩，它左等右等，未等来别的猴子，便把桃子平均分成五堆，还剩一个，它就把剩下的一个扔到海里，自己拿起了5堆中的一堆。第二个猴子来了，它把剩下的桃子分成五堆，把剩下的一个又扔掉了，然后拿起一堆。以后每个猴子来了都是如此办理，问原来至少有多少个桃子？最后海滩上至少剩下多少桃子？

方法一：
N=5A1＋1
4A1=5A2＋1
4A2=5A3＋1
4A3=5A1＋1
4A4=5A5＋1
化简得 N=3121
方法二：
如果这堆桃子的个数可以被5只猴子平分5次，每次都可以分成回5等份，那么这堆桃子的个数至少要有：
5×5×5×5×5=3125(个)但是，现在的桃子答总数是不能被5整除的，必须减去1才可以被5整除。这个数可以是：
3125+1=3126(个)但又要求5次5等份之前都要减少1，一共减去5个，即3126-5=3121(个)。

• 题目：
  一逻辑学家误入某部 落，被囚于牢狱，酋长欲意放行，他对逻辑学家说：“今有两门，一为自由，一为死亡，你可任意开启一门。现从两个战士中选择一人负责解答你所提的任何一个问题（Y/N），其中一个天性诚实，一人说谎成性，今后生死任你选择。”逻辑学家沉思片刻，即向一战士发问，然后开门从容离去。逻辑学家应如何发问？

左边得门回答Y，右边得门回答N，如果是另一个战士来指出哪一个是死门，他会指左边得门还是右边得门呢？
如果是诚实得人回答，因为不诚实得人会指向生门，所以诚实得人也会指向生门。
如果是说谎得人回答，因为诚实得人会指向死门，所以不诚实得人会指向生门。

• 题目：
  有一牧场,已知养牛27头,6天把草吃尽；养牛23头,9天把草吃尽。如果养牛21 头,那么几天能把牧场上的草吃尽呢？说明：牧场上的草是不断生长的。”

：$x$，：$y$，：$z$
$27\ast 6\ast x-6y=z$
$23\ast 9\ast x-9y=z$
得，$15x=y$
得，$72x=z$
$21\ast t\ast x-t\ast 15x=72x$
得t=12

• 题目：
  有两位盲人，他们都各自买了两对黑袜和两对白袜，八对袜了的布质、大小完全相同，而每对袜了都有一张商标纸连着。两位盲人不小心将八对袜了混在一起。他们每人怎样才能取回黑袜和白袜各两对呢？

标签撕开，每人拿一只。
放太阳下晒，温度高的是黑色袜子。

• 题目：
  你有两个罐子，50个红色弹球，50个蓝色弹球，自己可以按照设想的方法放弹球，放完以后随机选出一个罐子，随机选取出一个弹球放入罐子，怎么给红色弹球最大的选中机会？在你的计划中，得到红球的准确几率是多少？

$\frac{1}{2}+\frac{1}{2}\ast \frac{49}{99}$

• 题目：
  1元钱一瓶汽水,喝完后两个空瓶换一瓶汽水,问：你有20元钱,最多可以喝到几 瓶汽水？

不够的时候，找人借瓶子。
20+ 10+5+3+1+1 = 40瓶.

• 题目：
  在9个点上画10条直线,要求每条直线上至少有三个点？

X O X
O X O
X X X
O X O
X O X