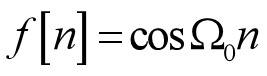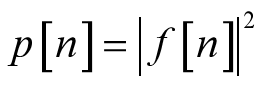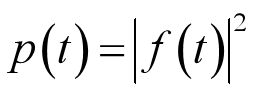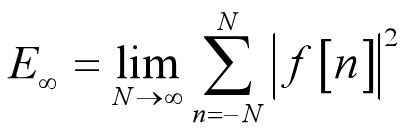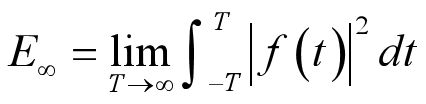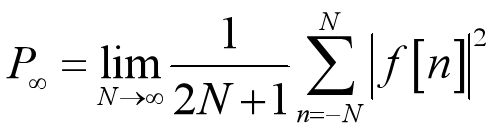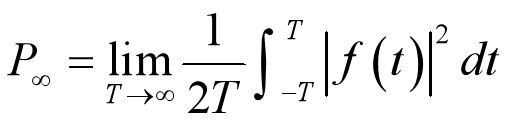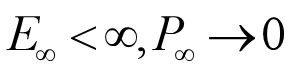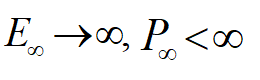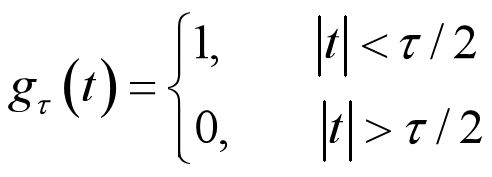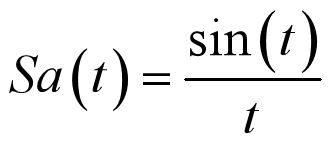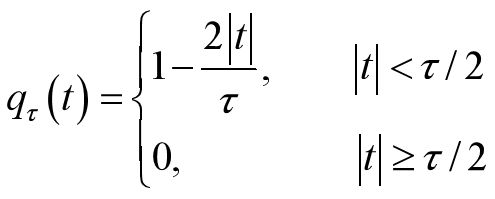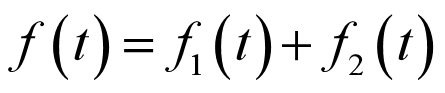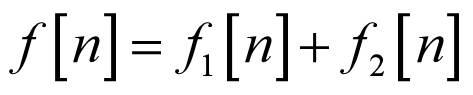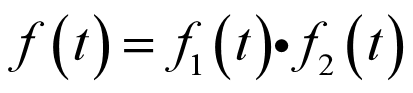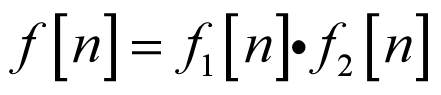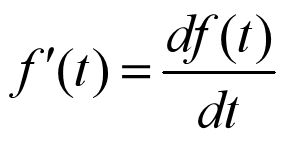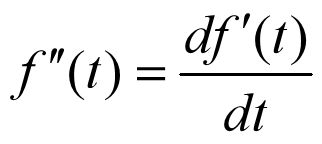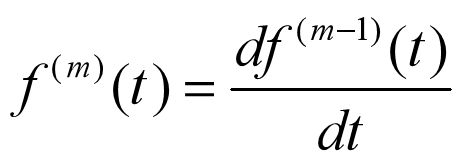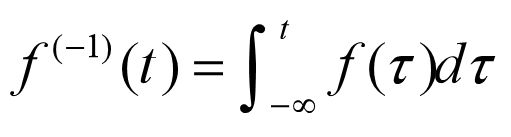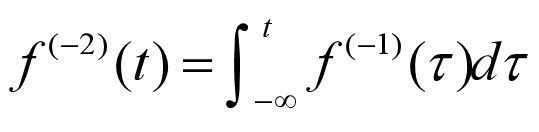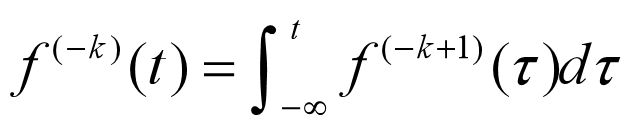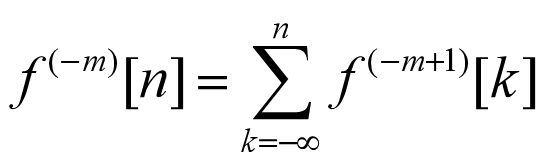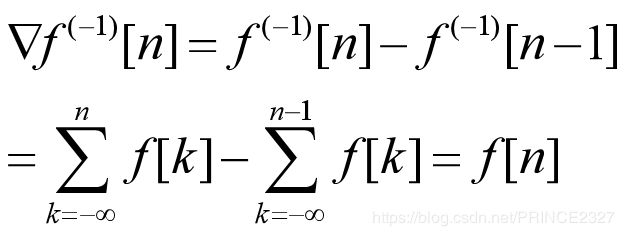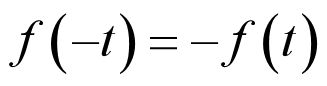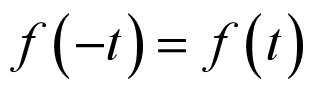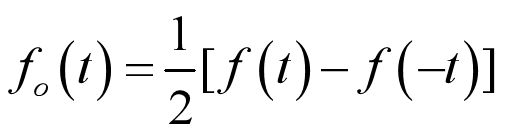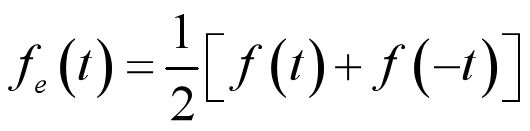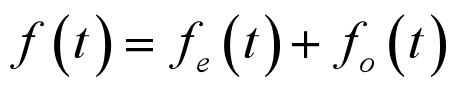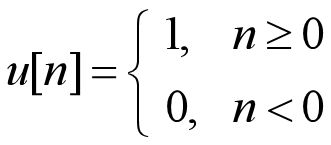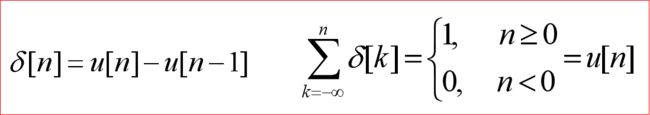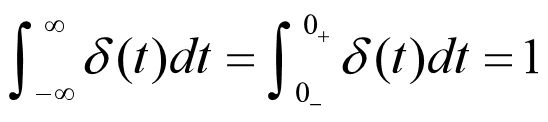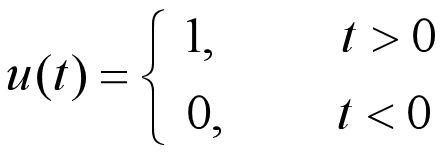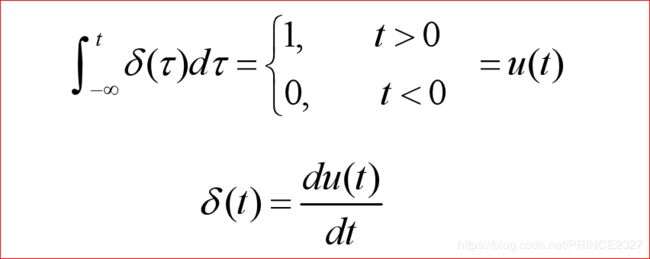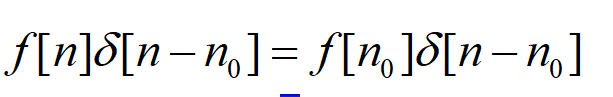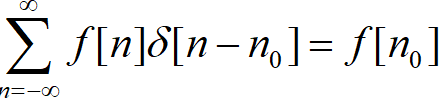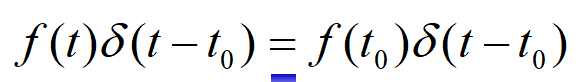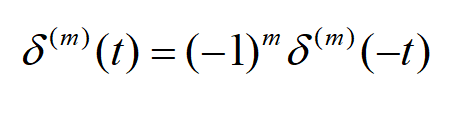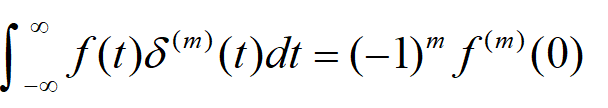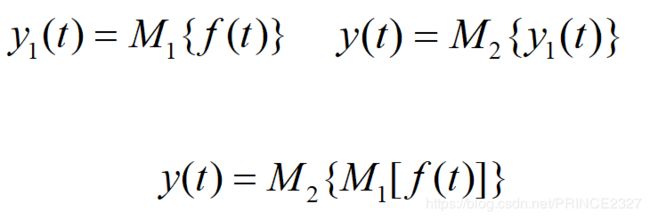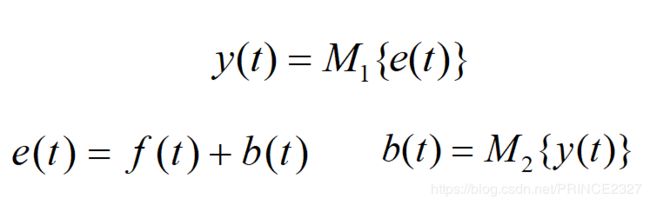信号与系统——初识到理解(第二章——信号与系统)
目录
- 第二章 信号与系统
- 2.1 什么是信号及信号如何表征
- 2.1.1信号的概念
- 2.1.1信号的表征方法
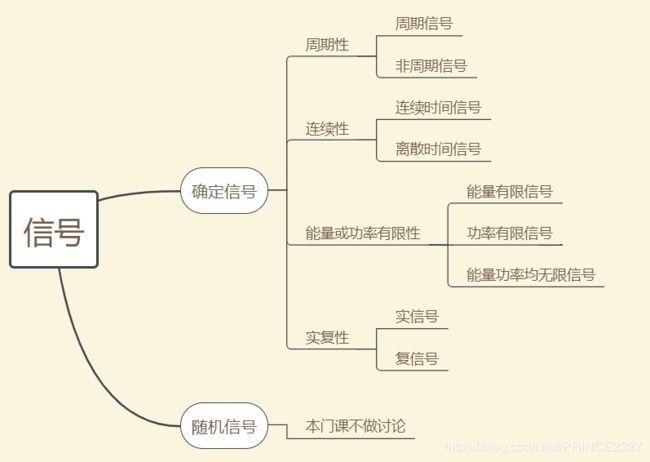
- 2.2 信号如何分类
- 2.2.1 信号类别及基本概念
- 2.2.2 确定信号与随机信号
- 2.2.3 连续时间信号与离散时间信号
- 2.2.4 周期信号与非周期信号
- 2.2.5 能量信号与功率信号
- 2.2.6 实信号与复信号
- 2.3 常见信号
- 2.3.1 因果信号
- 2.3.2 反因果信号
- 2.3.3 时限信号
- 2.3.4 左(右)边信号
- 2.3.5 双边信号
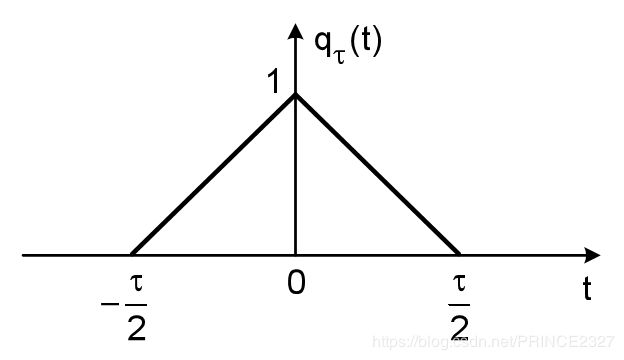
- 2.3.6 门信号
- 2.3.7 采样信号
- 2.3.8 三角脉冲信号
- 2.4 信号的运算
- 2.4.1 信号加法
- 2.4.2 信号乘法
- 2.4.3 连续时间信号的微分与积分
- 2.4.4 离散时间信号的差分与求和
- 2.4.5 信号的奇部与偶部
- 2.5 特殊的一类信号——奇异信号
- 2.5.1 离散时间单位冲激信号与单位阶跃信号
- 2.5.2 连续时间单位冲激信号与单位阶跃信号
- 2.5.3 单位脉冲信号的性质
- 2.6 什么是系统及系统如何表征
- 2.6.1 系统的定义
- 2.6.2 系统的表征
- 2.7 系统的连接方式
- 2.7.1 系统的并联
- 2.7.2 系统的级联(串联)
- 2.7.3 系统的反馈连接
- 2.8 系统的性质
- 2.8.1 系统的记忆性
- 2.8.2 系统的因果性
- 2.8.3 系统的可逆性
- 2.8.4 系统的稳定性
- 2.8.5 系统的时不变性
- 2.8.6 系统的线性
- 2.9 本章小结
第二章 信号与系统
2.1 什么是信号及信号如何表征
2.1.1信号的概念
在第一章我们其实已经提到了信号的概念,这里我们再给出简要的阐述:信号是承载信息的工具。正如概念所说,所有带有信息的载体都可以被称为信号(而不仅仅是有效信息)。例如最简单的语音信号,通过语音信号人们就可以相互传递信息。甚至是宇宙中某个星体的某种行为,通过观察它的行为,人们就可以大致推测出星体所处的状态,所以这也可以被称为一种信号。
2.1.1信号的表征方法
上述定义告诉我们,信号的表示方法数不胜数,从蚂蚁触角的移动到卫星传送的数据,都可以被定义为信号。由于信号的表示方法各不相同,为了统一与方便研究,在本门课中我们采用数学函数建模的方式表征信号。
2.2 信号如何分类
在初步了解了什么是信号以后,很自然地我们需要知道信号可以怎么分类。
2.2.1 信号类别及基本概念
1.确定信号:可以用确定表达式描述的信号。
2.随机信号:不可以用确定表达式描述的信号。信号值常被认为是一个随即变量。
3.连续时间信号:自变量连续取值且自变量为时间的信号。(事实上信号的自变量并不一定要是时间,例如图像信号)常记作f(t)。
4.离散时间信号:自变量不连续取值,只定义在某些离散时间整数点上的信号。(也称作离散时间序列)常记作f[n]。
5.周期信号
(a) 对于连续时间信号f(t)来说,若存在一个最小正数T,对于任意t有:f(t+T)=f(t),则称f(t)是以T为周期的周期信号,T称为该信号的基波周期。
(b)对于离散时间信号f[n]来说,若存在一个最小正整数N(由于离散时间信号只定义在整数点上,故此处相对连续时间信号来说多了整数的约束),使得对于任意的n有:f[n+N]=f[n],则称f[n]是以N为周期的周期信号,N称为该信号的基波周期。
6.非周期信号:除周期信号外的信号。
7.能量有限信号:总能量为有限数的信号(在后面会详细讲解)
8.功率有限信号:平均功率为有限数的信号(在后面会详细讲解)
9.能量功率均无限信号:能量和功率均为无穷的信号(非重点)
10.实信号:信号值为实数的信号。
11.复信号:信号值为复数的信号。(注意是根据信号值的实复性来区分实信号和复信号。不论对于哪种信号,其自变量都为实(t或n))
2.2.2 确定信号与随机信号
确定信号:可以用确定表达式描述的信号。
随机信号:不可以用确定表达式描述的信号。信号值常被认为是一个随即变量。
值得注意的是,此处区分确定性是以是否有明确的表达式区分的,所以即使有些信号可以画出图像,但若没有明确的表达式,我们也认为这一类信号是随机信号。
另外,确定信号的‘确定表达式’是作用在整个自变量轴的,也就是说必须要从负无穷到正无穷,每一段上都有确定的表达式,这样的信号才能被称为确定信号。考虑如下信号:
f 1 ( t ) = cos t f_{1}(t)=\cos{t} f1(t)=cost
f 2 ( t ) f_{2}(t) f2(t):随机信号
f 3 ( t ) = f 1 ( t ) + f 2 ( t ) f_{3}(t)=f_{1}(t)+f_{2}(t) f3(t)=f1(t)+f2(t)
即信号3为信号1(确定信号)与信号2(随机信号)加和的结果,由于随机信号的扰动,即使扰动宽度非常小,在最后加和的结果里,总有一部分是无法用表达式确定的,故信号3是一个随机信号,这样我们就得到了一个结论:
一般地,确定信号与随机信号的加和结果仍为随机信号
2.2.3 连续时间信号与离散时间信号
连续时间信号:自变量连续取值且自变量为时间的信号。(事实上信号的自变量并不一定要是时间,例如图像信号)常记作f(t)。
离散时间信号:自变量不连续取值,只定义在某些离散时间整数点上的信号。(也称作离散时间序列)常记作f[n]。
对于以上内容做以下几点说明:
1.连续或离散是针对自变量的取值来说的,这和高等数学中的函数连续性有所不同。考虑下图信号:
从函数角度来看,这显然不是一个连续函数。但在信号与系统中,由于上图信号的自变量t可以连续取值,故我们认为它是一个连续信号。连续信号有时也称为模拟信号。
2.一个离散时间信号的例子如下图:
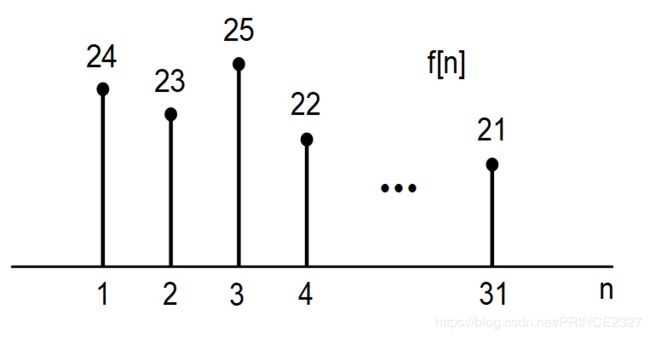
相对于连续时间信号的不同就是其自变量n仅仅定义在连续点上,如上图所示。在画离散时间信号的波形图时,横坐标为n,不需要标注正方向箭头且没有纵坐标。
2.2.4 周期信号与非周期信号
周期信号
(a) 对于连续时间信号f(t)来说,若存在一个最小正数T,对于任意t有:f(t+T)=f(t),则称f(t)是以T为周期的周期信号,T称为该信号的基波周期。
(b)对于离散时间信号f[n]来说,若存在一个最小正整数N(由于离散时间信号只定义在整数点上,故此处相对连续时间信号来说多了整数的约束),使得对于任意的n有:f[n+N]=f[n],则称f[n]是以N为周期的周期信号,N称为该信号的基波周期。
非周期信号:除周期信号外的信号。
对于信号的周期性做以下几点说明:
1.考虑如下连续时间信号: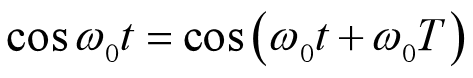
周期为:
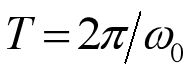
这符合我们中学的认知。但对于离散时间信号也是如此吗?
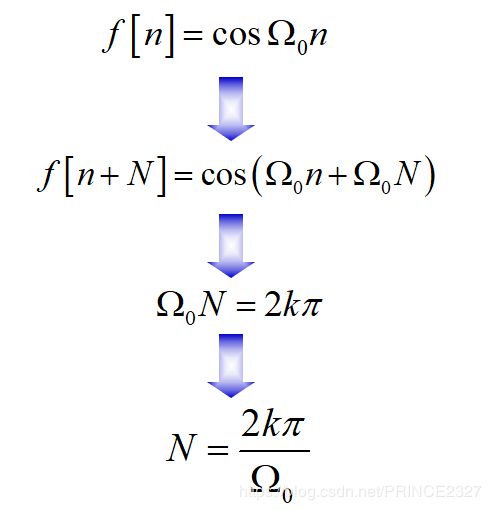
由于N只能取整数的限制,只有当频率为 π \pi π的整数倍时,N才有可能为整数。也就是说,对于离散正弦序列,并不一定是周期信号,只有满足一定条件才可能成为周期信号。
2.2.5 能量信号与功率信号
能量有限信号:总能量为有限数的信号(在后面会详细讲解)
功率有限信号:平均功率为有限数的信号(在后面会详细讲解)
下面对于信号的能量和功率做如下说明:
1.瞬时功率
2.总能量
离散信号:
连续信号:
3.平均功率
4.对于能量有限信号必定有平均功率为0,即:
5.对于功率有限信号必定有能量无穷,即:
6.以上结论基于微积分与电子电路基础相关知识。
2.2.6 实信号与复信号
实信号:信号值为实数的信号。
复信号:信号值为复数的信号。(注意是根据信号值的实复性来区分实信号和复信号。不论对于哪种信号,其自变量都为实(t或n))
2.3 常见信号
2.3.1 因果信号
定义:在t(n)<0时刻,信号值恒为0的信号
如下图:
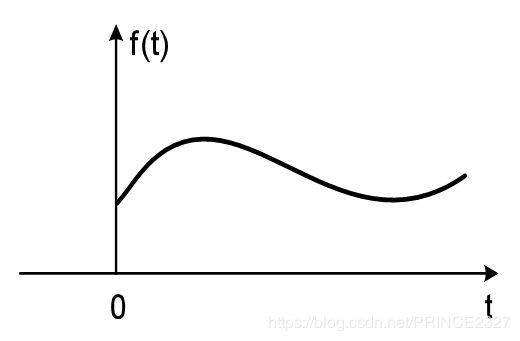
PS:因果信号只关注负时刻信号值是否恒为0,并不关注非负时刻信号值的状态。
2.3.2 反因果信号
定义:在t(n)>0时刻,信号值恒为0的信号
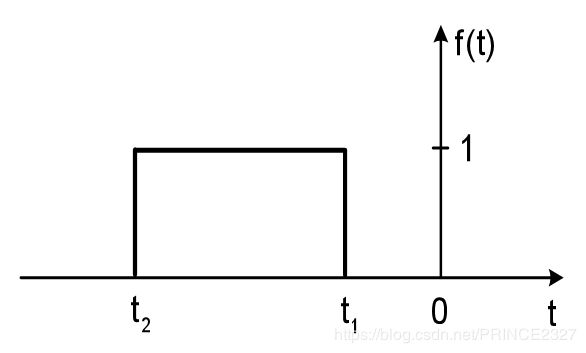
PS:与因果信号类似,反因果信号只关注正时刻信号值是否恒为0,而并不关注非正时刻信号值的状态。
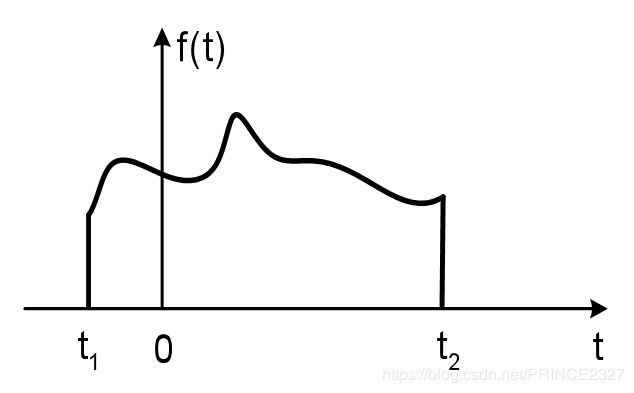
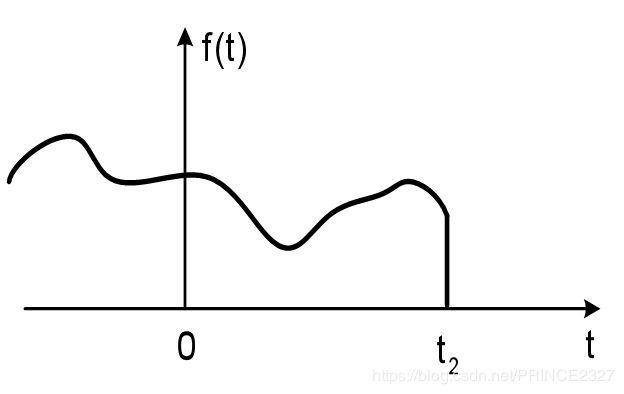
2.3.3 时限信号
定义:信号值不恒为0的时间有限长的信号(当然许多教材中有更加严密正规的定义,这里采用这一种定义旨在便于理解)
如下图:
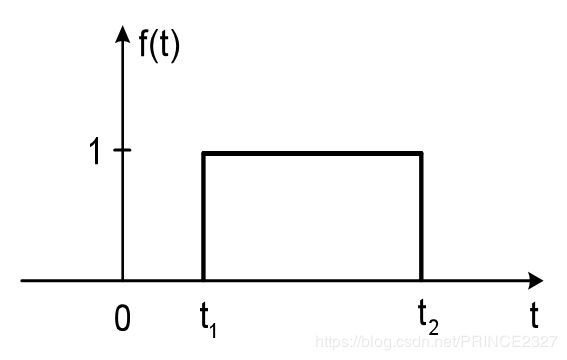
2.3.4 左(右)边信号
定义:对于t>(<)t1,信号值恒为0的信号(t1为有限数)
如下图:
PS:左(右)边信号只关注t1的右(左)边信号值是否恒为0,而并不关注另一侧的状态。讲到这里我们可以知道:时限信号既可以看成左边信号,也可以看成右边信号。因果信号一定是右边信号,反因果信号一定是左边信号,反之不然。
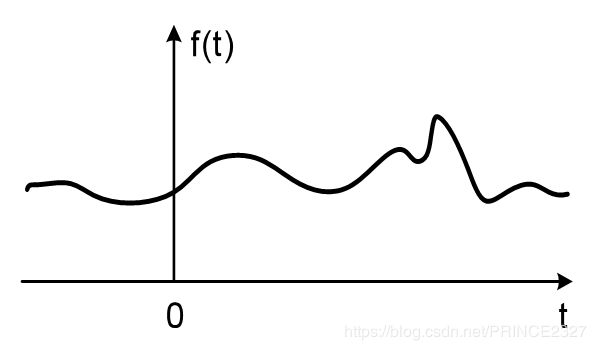
2.3.5 双边信号
定义:信号值不恒为0的部分持续到无穷的信号(正负无穷都要有)
如下图:
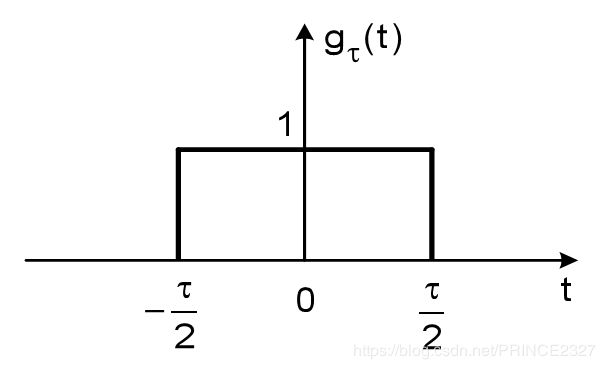
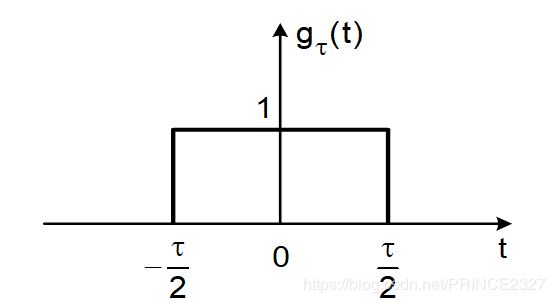
2.3.6 门信号
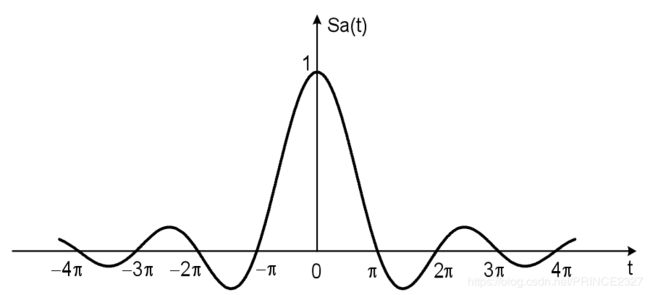
2.3.7 采样信号
2.3.8 三角脉冲信号
2.4 信号的运算
2.4.1 信号加法
所谓信号加法,就是将两个信号对应时刻信号值相加,所得到的结果是一个新信号。
2.4.2 信号乘法
所谓信号乘法,就是将两个信号对应时刻信号值相加,所得到的结果是一个新信号。
2.4.3 连续时间信号的微分与积分
积分
与数学中的微分操作类似
积分
基于上述讨论,可以将连续信号的微分与积分统一记为如下形式:

根据微积分知识,我们也可以得到如下结论:
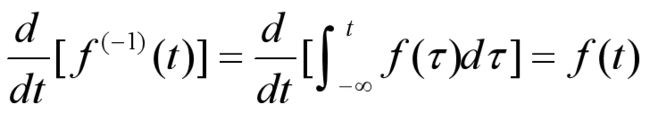
2.4.4 离散时间信号的差分与求和
差分
差分与连续时间信号中的微分相对应。主要有以下几种差分:
1.后向差分
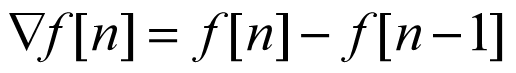
2.前向差分
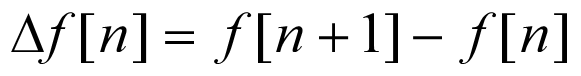
此后我们所说的差分若无特别说明则默认为后向差分
求和
此处求和对应于连续时间信号中的积分。可记为如下形式
2.4.5 信号的奇部与偶部
1.奇信号
2.偶信号
3.信号奇部
4.信号偶部
5.信号的奇部偶部分解
2.5 特殊的一类信号——奇异信号
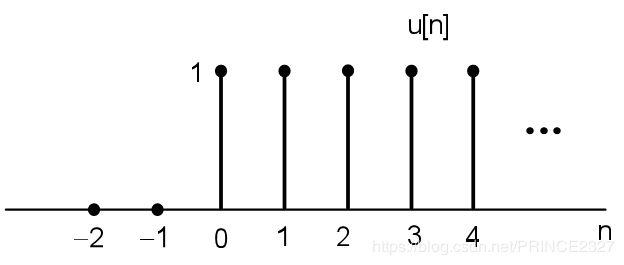
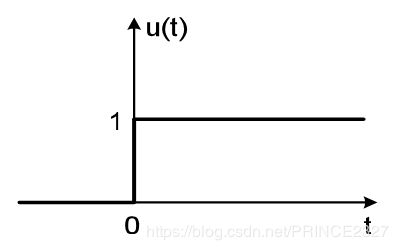
2.5.1 离散时间单位冲激信号与单位阶跃信号
1.离散时间单位冲击信号
定义:
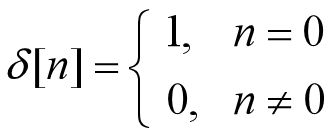
![]()
如上图,即为离散时间的单位脉冲信号。其‘脉冲’名字的由来源于其信号本身的特性,波形显示在0点处忽然突起,看起来就好像脉冲。而‘单位’并不是指其冲激强度为1,而是指其‘覆盖面积’为1。
2.离散时间单位阶跃信号
定义:
3.两者关系
观察可知,两者具有以下关系:
2.5.2 连续时间单位冲激信号与单位阶跃信号
1.连续时间单位冲激信号
此处对于连续时间单位冲激信号的引入,首先构造了前述的一个门函数:
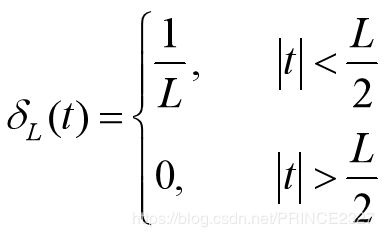
其波形图如下:
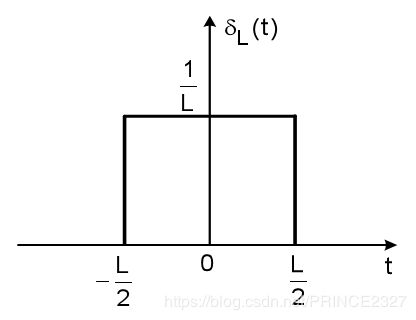
观察此函数。当L变窄时,此门函数的脉冲宽度就会变窄,同时,其脉冲强度将会增加。但不变的是,信号覆盖面积始终为1(单位名称的由来)。
当我们L趋近于0时,脉冲宽度趋近于0,同时脉冲强度趋近于无穷大。即:
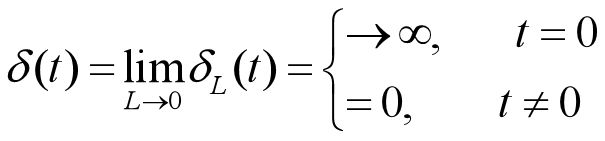
如此便引出了连续时间单位冲激信号:
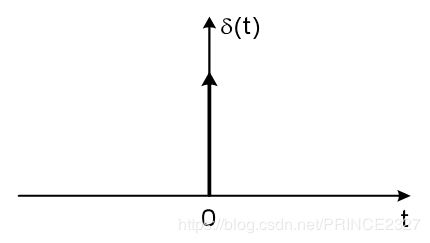
根据推导过程,我们可以得到如下结论:
2.5.3 单位脉冲信号的性质
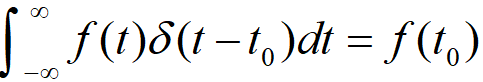
单位冲激信号的筛选性质的证明非常简单,此处略去。事实上,筛选性质只是结果,更多地,我们应该看到其背后蕴含的思想。如果说单位冲激信号的时间分辨率高到足以筛选出任意一个信号在任意一个时刻点的信号值。很自然地,我们就会想到利用冲激信号去进行复杂信号时域分解。基于其简单的表述形式及便捷的运算,我们确实这样做了(时域卷积)
3.微分性质
4.积分性质
5.尺度变换性质
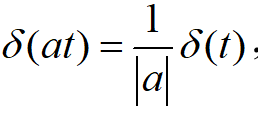
上述性质证明均略去,读者感兴趣可自行证明,更重要的是对于性质的理解及灵活运用。
2.6 什么是系统及系统如何表征
2.6.1 系统的定义
就像第一章概述这所说,系统是产生,加工,处理,传递信号的设备。
2.6.2 系统的表征
考虑到本门课用数学函数建模的方法去表示信号,故而表示对于信号有一定作用能力的系统,利用数学中的映射再合适不过。
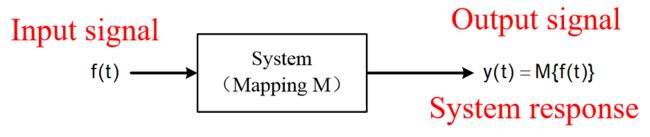
如上图,为一个最简单的输入输出装置。
当多输入单输出时:MISO系统
当单输入多输出时:SIMO系统
当多输入多输出时:MIMO系统
2.7 系统的连接方式
2.7.1 系统的并联
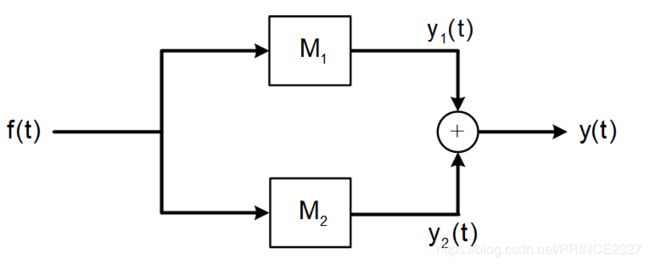
如上图即为两个系统M1,M2的并联。总输出是两个子系统输出加和。但值得注意的是,虽f(t)分成了两个箭头分别作用在两个系统上,但信号与系统中并没有分流的概念,也就是说任何一个子系统的输入信号是f(t),而不会是f(t)的一部分。
系统并联的输入输出关系如下:
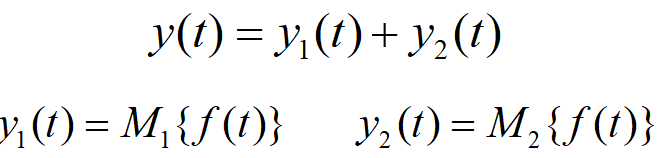
PS:任何多个系统的并联交换顺序后仍等效。
2.7.2 系统的级联(串联)
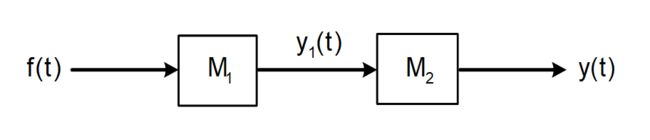
如上图即为系统的级联,级联也即串联。输入信号f(t)首先作用在一个系统M1上,得到的输出 y 1 ( t ) y_{1}(t) y1(t)再作为第二个系统M2的输入加入到第二个系统中,从而得到的输出就是整个系统的最终输出。
系统级联的输入输出关系可以如下表示:
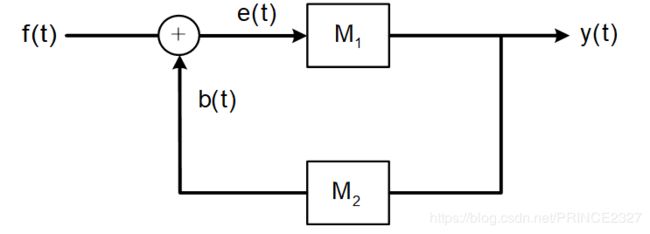
2.7.3 系统的反馈连接
2.8 系统的性质
2.8.1 系统的记忆性
定义:如果系统的输出仅仅取决于当前时刻的输入,那么称此系统是无记忆的,否则称为记忆系统。
这里需要注意以下几点:
1.此处强调的输出输入的时刻决定关系是对输出和输入来说的,输出是y(t),输入是f(t)。换句话说,是看y(t)和f(t)的关系如何,而并不关心输出输入表达式中的其他项。例如:y(t)=f(t)cos(t),对于这个系统,相信即使是一个初学者,也会毫不犹疑地判定它是一个无记忆系统。但对于y(t)=f(t)cos(t+1)呢,初次见面,看起来其中有t+1,好像可以据此判定其为记忆系统? 事实却并非如此,这就是之前强调的关注输入输出关系。t时刻的输出只取决于t时刻的输入,而cos(t+1)可以看作是系统本身的内部特性,故此系统仍然是一个无记忆系统。
2.记忆性是对系统而言的。
2.8.2 系统的因果性
定义:如果系统在某时刻的输出与未来的输入无关(即只取决于当前及过去时刻的输入),那么称这个系统为因果系统。
系统的因果性貌似告诉我们很多东西,自然界中绝大部分甚至全部系统都是因果系统,这也反映了‘时间不可倒流’的理论。
2.8.3 系统的可逆性
定义:如果对于任意不同的输入总会产生任意不同的输出,则称该系统是可逆的。
可逆性的数学表达式定义看起来好像和文字定义相差甚远。但细想发现它们事实上是一样的,如果说已知一个系统对于不同的输入总会产生不同的输出,也就是说不知道输入的情况下,只要我们知道映射关系,我们总能确定它的输入(而不必为究竟是哪一个输入而苦恼),这样必然可以创造一个系统用来读取原系统的输出并输出原系统的输入,这也就是逆系统的由来。
2.8.4 系统的稳定性
定义:对于任意有限输入,系统总能产生有限的输出,则称该系统是稳定系统。
2.8.5 系统的时不变性
定义:输出的延时等于延时的输出。
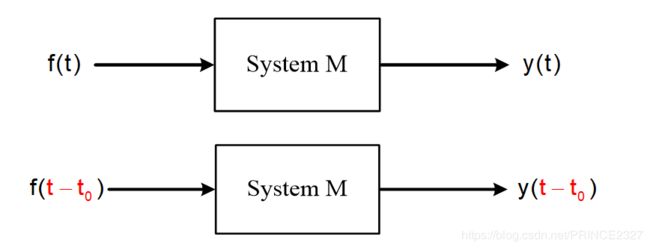
事实上时不变性意味着系统是平稳的,即系统中的元件参数等不随时间而改变。这保证了不论是今天做实验,或是明天做实验,都会得到相同的结果,只是在时间上有所延时
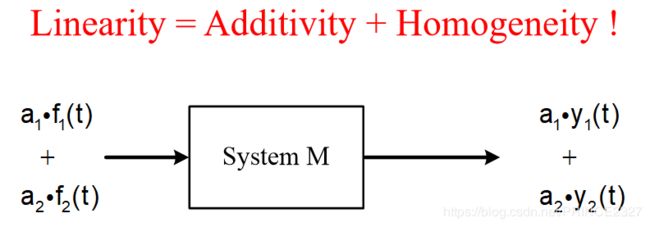
2.8.6 系统的线性
定义:同时满足可加性和齐次性。
PS:我们以后主要研究的系统为线性时不变系统。
2.9 本章小结
1.信号概念及常见信号。
2.奇异信号及性质。
3.信号的基本运算。
4.系统概念,连接方式及性质。
持续更新中,欢迎讨论与指正。