吴恩达机器学习第二周测试及编程练习

代码：https://github.com/LiuZhe6/AndrewNGMachineLearning

测验一：Linear Regression with Multiple Variables

第一题

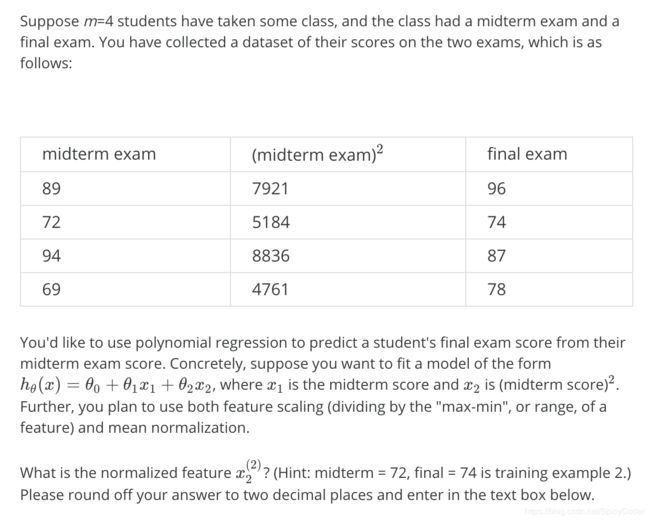
答案
0.52
分析
使用特征缩放，具体将特征值处以（最大值-最小值）或者范围即可，故5184/(100)^2 = 0.52（保留两位小数）

第二题

答案
C
分析：由于代价函数迅速下降并趋于平稳，说明å选的比较好。

第三题

答案
C
分析：根据题目，n为3（不包括x0）,故x应为14 * 4的矩阵，y为4*1的向量。

第四题

答案
B
分析：正规方程可以一步找到解（矩阵可逆情况下）

第五题

答案
B
分析：特征缩放可以帮助梯度下降算法更快的收敛。

---

测验二：Octave/Matlab Tutorial

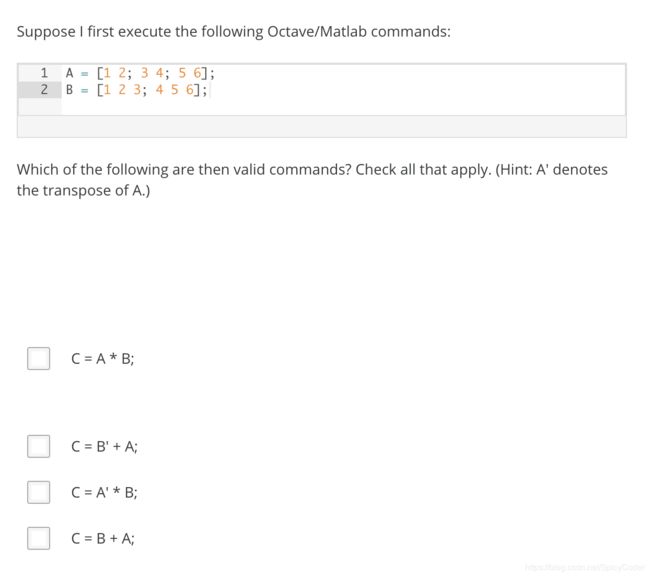
第一题

答案
A B

第二题

答案
A B
分析：octave下标从1开始

第三题

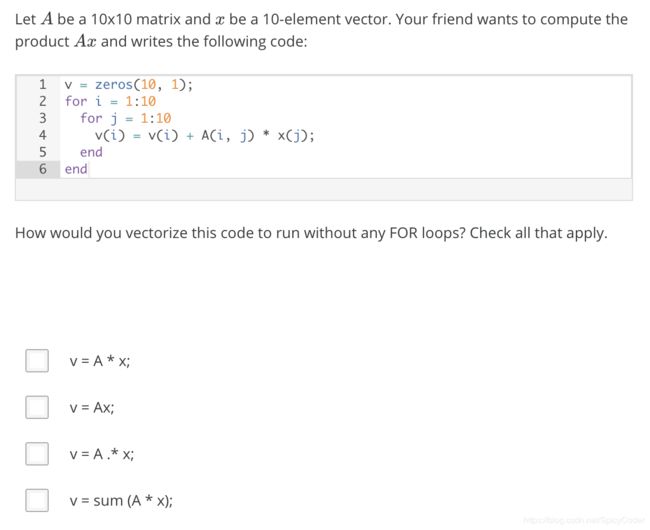
答案
A
分析：C选项是点乘，是把A矩阵的每一行乘以对应x向量的每一行，不合题意。故只有A。

第四题

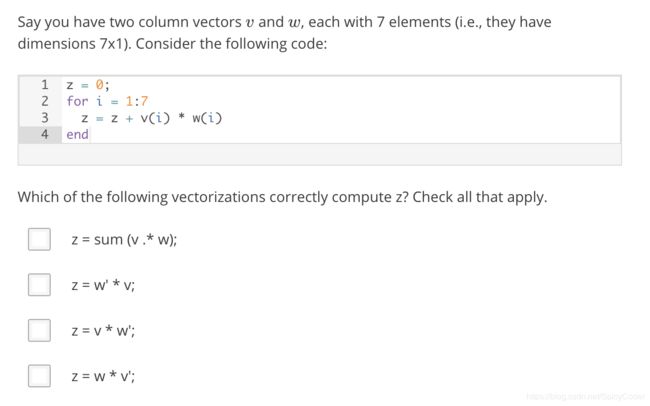
答案
A B
分析：A选项同上题分析，最后sum一下算出总和

第五题

答案
A B C
分析：D选项错误，若那样写则计算结果是X * X

---

tips ：macOS Mojave (10.14)使用homebrew安装的octave无法相应pause后的任意键输入，解决方案见macOS Mojave(10.14.4)系统Octave 5.1.0使用pause()函数无法响应按键事件

编程作业: Linear Regression

作业1:计算CostFunction

computeCost.m

%使用for循环(这样不好，效率太低)
% for i=1:m
%    hx = X(i,:) * theta;
%    J += (hx - y(i)) ^ 2;
% end;
% J = J / (2*m);


%向量化方法(推荐使用)
hx = X * theta - y;
J = sum(hx .^ 2)/(2*m);

作业2:梯度下降法

gradientDescent.m

	%for循环（效率低，而且精度不符合，不推荐）
    % n = length(X(1));
    % for j = 1 : n+1,
    %     sum = 0;
    %     for i = 1 : m,
    %         sum += (theta(1) * X(i,1) + theta(2) * X(i,2) - y(i)) * X(i,j);
    %     end;
    %     theta(j) -= alpha / m * sum;
    % end


    %向量化 (推荐)
    theta -= alpha / m * X' * (X * theta - y);

作业3:特征缩放(选做)

featureNormalize.m

% 得到X矩阵每一列的平均值
mu = mean(X);
% 得到X矩阵每一列的标准差
sigma = std(X);

X_norm = (X_norm - mu) ./ sigma;

作业4:代价函数-多特征（选做）

computeCostMulti.m

J = 1 / (2 * m) * (X * theta - y)' * (X * theta - y);

作业5:梯度下降-多特征（选做）

gradientDescentMulti.m

%向量化 (推荐)
theta -= alpha / m * X' * (X * theta - y);

预测 1650，3的价格
ex1_multi

% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
% Recall that the first column of X is all-ones. Thus, it does
% not need to be normalized.

mydata = ([1650 ;3] - mu) /sigma;
mydata = mydata';
mydata = [1,mydata];

price = mydata * theta; % You should change this


% ============================================================

结果：$300611.500728

作业6:正规方程-多特征（选做）

normalEqn.m

theta = pinv((X' * X)) * X' * y;

预测：1650，3的价格
ex1_multi.m

% ====================== YOUR CODE HERE ======================
price = [1, 1650 , 3] * theta; % You should change this


% ============================================================

结果：$293081.464335