时间复杂度和空间复杂度一头雾水？此文能帮你解决疑惑

算法分析

求解同一个问题时，可以有很多种不同的算法，那如何评价这些算法的好坏呢？
首先，大前提是算法是正确的，可执行的，然后再主要考虑以下三点：
①执行算法所耗费的时间——时间复杂度
②执行算法所耗费的空间——空间复杂度
③算法应易于理解、易于编写、易于调试

我们目标都是找到一个执行时间相对短的、占用空间少的、便于理解和编写的算法。这三点中的第三点是带有一定主观性的，毕竟每个人对待问题的理解方式不同，可能喜欢用不同的思路去书写算法，而前两点都是很客观的，我们用相关的计算方式可以得到专门的数学变量，来衡量一个算法的时间和空间耗费情况。

时间复杂度

一般的，我们将算法求解问题的输入量（或初始数据量）称为问题的规模，并用一个整数表示，我们习惯的设问题规模为n，算法中一条语句执行的次数称为频度，一个算法所耗费的时间就是每条语句的频度与执行一次所需时间的乘积之和。但每条语句执行一次的时间取决于机器的性能、运行速度、编译质量等很多方面，所以很难确定，于是我们就假设每条语句运行时间是单位时间，那么一次算法中所有语句的频度之和称为算法的时间耗费，用函数$T(n)$表示。

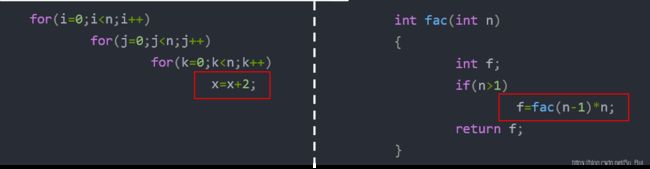
(1)	for(i=0;i<n;i++)
(2)		for(j=0;j<n;j++)
(3)			for(k=0;k<n;k++)
(4)				x=x+2;

上述算法片段，
语句(1) i 从0至n共n次循环，最后还需判断 i $⩾$ n才结束，所以执行n+1次，(1)频度为n+1；
语句(2)自身也是执行n+1次，但嵌套在第一个循环中，循环n次，所以需执行n*(n+1)次，(2)频度为n(n+1)；
语句(3)自身也是执行n+1次，但嵌套在第二个循环中，需执行n* n* (n+1)次，(3)频度为 n²(n+1)；
语句(4)嵌套在三个循环内，需执行n³次，(4)频度为n³。
所以该段算法的时间耗费：$T(n)=(n+1)+n\ast (n+1)+n^2(n+1)+n^3=2n^3+2n^2+2n+1$

可能这么说对于刚接触这些概念的人并不是很好理解，没关系，举几个直观的例子就很容易理解了。

例1: 我的老师给我布置了一些作业，一共有3个科目（程序设计、算法分析、软件测试）的作业，每个科目有10项作业，我这个人雨露均沾，完成每项作业的时间是一样的，设为单位时间1，那么试求我完成这些作业的时间耗费$T$是多少?

这里每项作业完成时间是单位时间1，每科10项作业，所以每个科目作业所需时间为10*1=10
一共3个科目，所以我完成作业的时间耗费$T=10+10+10=30$

问题升级： 如果将这里的已知量，换成变量，即每个科目有n项作业，其他条件不变，那我完成这些作业的时间耗费$T(n)$又是多少?

还是同样每项作业完成时间是单位时间1，每科n项作业，所以每个科目作业所需时间为n*1=n
一共3个科目，所以我完成作业的时间耗费$T(n)=n+n+n=3n$

例2： 换一种情景，这次只有一个科目（算法分析）老师给我布置作业，给我留了10项算法分析的题目，只不过我刚开始学习这个科目基础不是很好，我每做1个算法分析之前需要学习10项数据结构的知识点，然而，我数据结构也学得不扎实，每看1个数据结构的知识点就要学习10个C语言的知识点。假如我C语言学习的还不错，每个C语言的知识点学习时间是一样的，设为单位时间1，那么试求我完成这些作业的时间耗费$T$是多少?

1项算法分析需要10个数据结构的知识点，那么10项算法分析需要10*10=10²个数据结构的知识点
1个数据结构需要10个C语言的知识点，那么10²个数据结构需要10²*10=10³个C语言的知识点
1个C语言的知识点学习时间是单位时间1，所以10³个C语言的知识点所需时间为10³*1=10³
则我完成这些作业的时间耗费$T=10^3$

问题升级： 如果将这里的已知量，换成变量，即一共n项算法分析，1项算法分析需要n个数据结构的知识点，1个数据结构需要n个C语言的知识点，其他条件不变，那我完成这些作业的时间耗费$T(n)$又是多少?

1项算法分析需要n个数据结构的知识点，那么n项算法分析需要n*n=n²个数据结构的知识点
1个数据结构需要n个C语言的知识点，那么n²个数据结构需要n²*n=n³个C语言的知识点
1个C语言的知识点学习时间是单位时间1，所以n³个C语言的知识点所需时间为n³*1=n³
则我完成这些作业的时间耗费$T(n)=n^3$

例3： 再换一种情景，临近期末，我其他课程都已经结课了，就剩下算法分析这门课程，老师希望我多多练习，期末能考个好成绩，就给我留了128道算法分析。我这个人惰性很大，完成一点作业就觉得自己好像做了很多事情，所以我每天只完成剩下作业的一半就不想做了。也就是我第一天做64道，第二天做32道，第三天做16道……试求就剩最后1道题时我的时间耗费$T$

128道题，每天做一半，即$128\ast \frac{1}{2}\ast \frac{1}{2}\ast \frac{1}{2}\ast \dots \ast \frac{1}{2}$
求的是几天之后$128\ast \frac{1}{2}\ast \frac{1}{2}\ast \frac{1}{2}\ast \dots \ast \frac{1}{2}=1$ ?
 
即解关于$T$的方程$128\ast (\frac{1}{2}{)}^T=1$
 
                                       $(\frac{1}{2}{)}^T=\frac{1}{128}$
 
                                           $2^T=128$
 
                                        $\therefore T={\log }_{2}128$

问题升级： 如果将这里的已知量，换成变量，即一共n道算法分析，那我完成这些作业的时间耗费$T(n)$又是多少?

思路也是一样
即解关于$T(n)$的方程 $n\ast (\frac{1}{2}{)}^T=1$
 
                                     $\therefore T(n)={\log }_{2}n$

如果这几个例子基本都能理解的话，那么恭喜，你已具备了一定的对算法时间耗费分析的能力，对程序有所了解的人也已经发现，上述3个例子，分别对应的就是程序的顺序结构、嵌套循环结构、递归结构时间耗费的计算方法。

下面就要引入新的概念：当问题的规模n趋向无穷大时，我们把时间耗费$T(n)$的数量级（阶）称为算法的渐进时间复杂度。即如果存在一个函数$f(n)$使得$\underset{n\to \infty }{\lim }\frac{T(n)}{f(n)}$的值是一个不等于0的常数，那么$T(n)$和$f(n)$就是同阶的，记作$T(n)=O(f(n))$。我们称$T(n)=O(f(n))$是算法的渐进时间复杂度，在对算法分析时，习惯将渐进时间复杂度简称为时间复杂度。

记号“$O$”是数学符号，具有严格的数学定义：若$T(n)$和$f(n)$是定义在正整数集合上的两个函数，当存在两个正的常数 $c$ 和 $n_0$，使得对所有的$n⩾n_0$，都有$T(n)⩽c\cdot f(n)$成立，则$T(n)=O(f(n))$。

看到这肯定很多人一脑子问号，我这刚想明白$T(n)$是怎么计算的，这又说了一大堆神马东西，完全看不懂啊！不慌，我们第一次提到一个概念，肯定是要用官方的概念下定义，这样比较专业和严谨。但是，我们分析和理解的时候就可以用很通俗的方法去解释。

可能大家会有很多疑问：

• 为什么要讨论n趋向无穷大？
• 我没学过高数不懂什么是极限，我该怎么求$O(f(n))$ ?
• 既然都有$T(n)$为什么还要引入$O(f(n))$ ? 下面我就来一一解答。

为什么要讨论n趋向无穷大？

难道n=10、100、1000…没有研究价值么，为什么要讨论n趋向无穷大呢？话不能说的太绝对，n=10、100、1000…肯定有它存在的意义，但n趋向无穷大时数据更宏观。

打个比方，我国神威·太湖之光超级计算机，2019年11月18日，全球超级计算机500强榜单中，排名第三位。我用它和我手里的笔记本电脑同时运行10以内的加减法，二者的运行时间的差距肉眼可能都无法察觉，那我能说神威·太湖之光和我手里的笔记本电脑的运算能力是几乎一样的么？显然是不行的，要是让二者同时计算卫星发射的轨迹、飞行路线还有天体间的距离这种庞大的数据，神威·太湖之光可能在几秒钟内完成，而我的笔记本电脑可能算上几天几夜都算不出来。

所以就是说在输入规模n比较小的时候，性能好和性能不好的算法很难比较出差距，只有当n不断扩大，算法性能的好坏就变得明显。

我没学过高数，不懂什么是极限，我该怎么求$O(f(n))$?

记住3个原则，轻松搞定由$T(n)$推出$O(f(n))$
①只保留$T(n)$中最高阶项，其余统统省略。
例如：$T(n)=2n^3+2n^2+2n+1$ 只保留$2n^3$
②系数为常数时省去系数
例如：$T(n)=2n^3$ 省去系数$2$，只保留$n^3$
③$T(n)$是常数时，$T(n)=O(1)$
例如：$T(n)=3$时，$T(n)=O(1)$

$T(n)=2n^3+2n^2+2n+1⟹T(n)=O(n^3)$
$T(n)=3n⟹T(n)=O(n)$
$T(n)=n^3⟹T(n)=O(n^3)$
$T(n)=10{\log }_{2}n⟹T(n)=O({\log }_{2}n)$
$T(n)=30⟹T(n)=O(1)$

既然都有$T(n)$为什么还要引入$O(f(n))$ ?
用官方一点的话说，$O$比$T(n)$能更宏观的体现算法的性能。什么叫更宏观呢，就是“不要在意细节”。根据上面$O$的计算方法可以看出，$O$相比于$T(n)$，$O$忽略了系数并只保留了最高阶，为什么这样就更宏观了？

打个比方，2019年11月7日，福布斯发布2019年度中国富豪榜，马云蝉联榜首，财富值2701亿元，而我总资产为1000元，不难看出马云比我有钱，甚至100个我的资产加起来也比不过马云。因为我和马云在资产上，完全不属于一个层次。这就是不同数量级面前，当数据规模很大时，系数对其结果的影响变得微乎其微，我们可以将其忽略。

再比如，我们常见的游戏和平精英，每个人都会有一个段位（青铜、白银、黄金、铂金、钻石、皇冠、王牌、战神），当我们组队匹配，4个人的队伍中段位最高的1个人是“战神”，那么无论其他人的段位如何，这一局游戏匹配到的对手也多数都是战神段位，也就是所谓的“战神局”，由此可见最高段位的人对其的影响。这就是为什么$O$只保留了最高阶，一个算法的时间开销主要取决于运行频度最大的那条语句，其它语句对整体的影响就可以忽略。

如何确定算法哪条语句是运行频度最大（时间耗费最多）的语句?

一般的，涉及嵌套循环的算法，最里层循环的语句运行频度最大，直观点来说，就是如果代码排版没有问题，缩进量最多的一句运行频度最大；带有递归的算法，发生递归或者递归出口运行频度最大。

联系生活可以帮助我们理解，但是，这是一个数学关系，我们还是要用数据说话。

先来看不同数量级的差距

$n$	$n^2$	$n^3$
10	100	1000
100	10000	1000000
1000	1000000	1000000000
10000	100000000	1000000000000
100000	10000000000	1000000000000000

可以看到，数据不断增大的过程中，$n、n^2、n^3$三个数量级之间的差距越来越大。

再看看系数是否会对数量级之间的差距有影响

$n$	$500n$	$n^3$
10	5000	1000
100	50000	1000000
1000	500000	1000000000
10000	5000000	1000000000000
100000	50000000	1000000000000000

看得出来，一开始的时候数据较小，系数确实对其有些影响，随着数据的不断增大，$500n$与$n^3$差距也不断扩大，系数500对其的改变就相对很渺小。

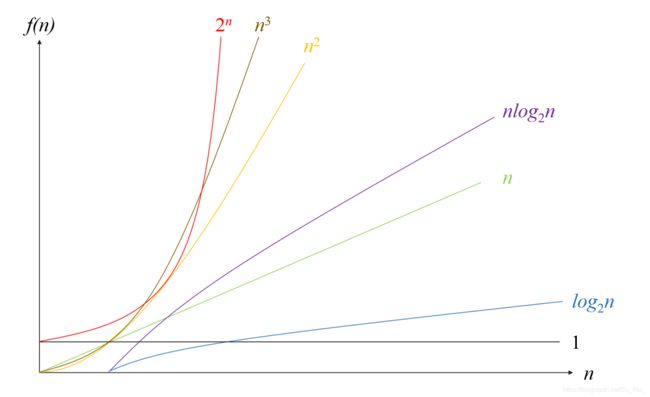
上图列出了几种常见函数的增长率，n较小时，几个函数值得差距并不大，随着n不断增大，几个函数的差距越来越明显。不难看出，时间复杂度为$O(2^n)$的算法效率极低，$n$稍大时就无法应用，$O(n^2)$、$O(n^3)$比起$O(2^n)$能稍好一些，但效率也不是很高，$O(nlo{g}_{2}n)$、$O(n)$、$O(lo{g}_{2}n)$、$O(1)$这几个相对比较平稳，是我们理想的状态。

常见的时间复杂度，按数量级递增排列依次是：常数阶$O(1)$、对数阶$O(lo{g}_{2}n)$、线性阶$O(n)$、线性对数阶$O(nlo{g}_{2}n)$、平方阶$O(n^2)$、立方阶$O(n^3)$、… 、k次方阶$O(n^k)$、指数阶$O(2^n)$，从时间角度，我们希望一个算法时间复杂度的数量级越低越好。

总结：时间复杂度 $O$ 的计算过程

1.找到算法执行频度最高的语句
2.计算出该语句的时间耗费$T(n)$
3.通过$T(n)$求出时间复杂度$O$

很多时候算法的时间复杂度不单纯与问题规模有关，还与输入的数据状态有关。比如，我要实现从小到大排序，同样输入5个数据，一个输入为1 2 3 4 5，另一个为5 4 3 2 1，两种状态下同一算法的时间复杂度也有不同。所以根据输入可能出现的最好情况，估计出最优时间复杂度，根据输入可能出现的最坏情况，估计出最坏时间复杂度，有时，我们也对输入数据的分布做出某种假定，讨论算法的平均时间复杂度。在分析和评估算法时我们更多考虑的是最坏时间复杂度和平均时间复杂度。

空间复杂度

一个程序执行时所占用的空间主要分成两部分：

• 静态存储空间
  这部分空间主要来自于指令、函数定义、常数、变量、输入数据等，这部分是每个程序都需具备的基本内容，与算法无关。

• 辅助存储空间
  这部分空间是算法执行时定义的，帮助算法临时存储、交换、转移数据等，与算法有关。

一个算法的空间耗费$S(n)$主要考虑的就是辅助存储空间，和时间复杂度类似，同样把空间耗费函数$S(n)$的数量级称为渐进空间复杂度，简称空间复杂度。

大部分算法，只要不涉及到动态分配的空间以及递归、栈所需的空间，空间复杂度通常为$O(1)$；如果我定义了一个临时数组Temp用来存放输入数据，临时数组的大小等于输入规模n，那算法空间复杂度为$O(n)$；一般递归分配临时辅助空间时的空间复杂度为$O(lo{g}_{2}n)$。

总结

时间复杂度和空间复杂度是评价算法的基本标准，但并不局限于这两点，特定的算法可能还有其他的方面需要考虑，比如排序算法还需考虑排序的稳定性等。

平时算法分析对空间复杂度的关注略逊于时间复杂度，并不是说空间复杂度不重要，只是分析一个算法性能时，我们更先考虑时间复杂度。有时如果空间内存充足，我们可能会牺牲存储空间来提高运行速度。原因也不难理解，就是机器的内存空间的提升比运行速度的提升相对容易一点，就比方说，我文件很多，一个优盘装不下，那我可以准备两个、三个优盘，而如果优盘传文件的速度慢，那可能就需要从硬件性能、底层架构、传输协议等很多方面去优化才能提升传输速度。

写在最后

参考资料:
《数据结构-用C语言描述》高等教育出版社
《计算机算法设计与分析》电子工业出版社
时间复杂度-百度百科
空间复杂度-百度百科

（只是分享个人学习时的想法和理解，如有问题还望大佬指点）