Python【逻辑回归】算法
文章目录
- 1、sklearn实现
- 2、算法实现
- 2.1、创建样本
- 2.2、Sigmoid函数
- 2.3、梯度上升
- 3、梯度下降原理
- 4、附录
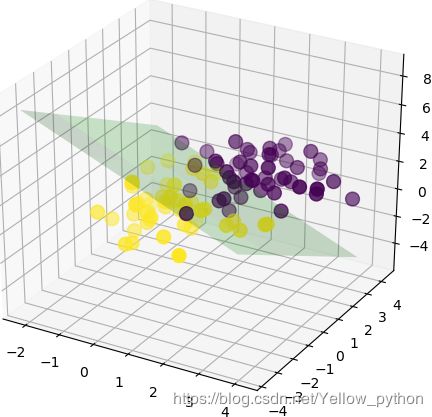
1、sklearn实现
from sklearn.linear_model import LogisticRegression
from sklearn.datasets.samples_generator import make_blobs
import numpy as np, matplotlib.pyplot as mp
from mpl_toolkits import mplot3d
# 创建数据
X, y = make_blobs(centers=[[2, 2, 2], [0, 0, 0]], random_state=3)
# 训练模型
model = LogisticRegression()
model.fit(X, y)
# 系数(coefficient)和截距
k = model.coef_[0]
b = model.intercept_[0]
# 可视化
fig = mp.figure()
ax = mplot3d.Axes3D(fig) # 获取三维坐标轴
# 散点图
ax.scatter(X[:, 0], X[:, 1], X[:, 2], s=99, c=y)
# 决策边界
x1 = np.arange(X[:, 0].min()-1, X[:, 0].max()+1, 2)
x2 = np.arange(X[:, 1].min()-1, X[:, 1].max()+1, 2)
x1, x2 = np.meshgrid(x1, x2)
x3 = (b + k[0] * x1 + k[1] * x2) / - k[2] # 边界函数
ax.plot_surface(x1, x2, x3, alpha=0.2, color='g')
mp.show()
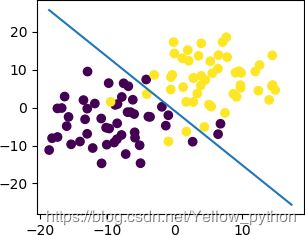
2、算法实现
import numpy as np, matplotlib.pyplot as mp
from sklearn.datasets import make_blobs
"""创建随机样本"""
X, Y = make_blobs(centers=2, cluster_std=5)
"""数据处理"""
X = np.insert(X, 0, 1, axis=1) # 增加一列,用于矩阵相乘
Y = Y.reshape(-1, 1)
"""sigmoid函数"""
sigmoid = lambda x: 1 / (1 + np.exp(-x))
"""梯度上升"""
d = X.shape[1] # 维数
theta = np.mat([[1]] * d) # 初始化回归系数
for i in range(5999, 8999):
alpha = 1 / i # 步长(先大后小)
h = sigmoid(X * theta)
theta = theta + alpha * X.T * (Y - h) # 最终梯度上升迭代公式
"""数据可视化"""
x1, x2 = X[:, 1], X[:, 2]
mp.axis([x1.min() + 1, x1.max() + 1, x2.min() + 1, x2.max() + 1])
mp.scatter(x1, x2, c=Y.reshape(-1)) # 原始样本点
x = np.array([x1.min(), x1.max()])
y = (-theta[0, 0] - theta[1, 0] * x) / theta[2, 0] # 决策边界
mp.plot(x, y)
mp.show()
2.1、创建样本
X, y = make_blobs(centers=2, cluster_std=6)
X = np.insert(X, 0, 1, axis=1) # 增加一列,用于矩阵相乘
y = y.reshape(-1, 1) # 转换成n*1维的矩阵
X = ( 1 x 12 x 13 1 x 22 x 33 ⋮ ⋮ ⋮ 1 x n 2 x n 3 ) n 行 3 列 y = [ y 1 y 2 ⋮ y n ] n 行 1 列 X = \begin{pmatrix} 1 & x_{12} & x_{13}\\ 1 & x_{22} & x_{33}\\ \vdots & \vdots & \vdots\\ 1 & x_{n2} & x_{n3}\\ \end{pmatrix}_{n行3列} y=\begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}_{n行1列} X=⎝⎜⎜⎜⎛11⋮1x12x22⋮xn2x13x33⋮xn3⎠⎟⎟⎟⎞n行3列y=⎣⎢⎢⎢⎡y1y2⋮yn⎦⎥⎥⎥⎤n行1列
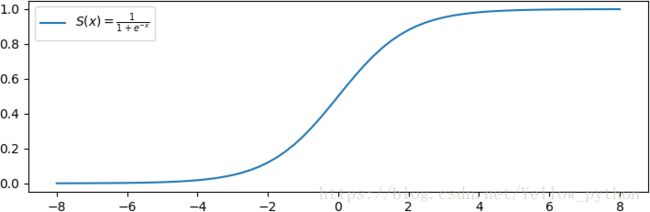
2.2、Sigmoid函数
亦称S型生长曲线。在信息科学中,常被用作神经网络的阈值函数,将变量映射到(0,1)
import numpy as np, matplotlib.pyplot as mp
sigmoid = lambda x: 1 / (1 + np.exp(-x)) # sigmoid函数
x = np.linspace(-8, 8, 65)
mp.plot(x, sigmoid(x), label=r'$S(x)=\frac{1}{1+e^{-x}}$')
mp.legend() # 图例
mp.show()
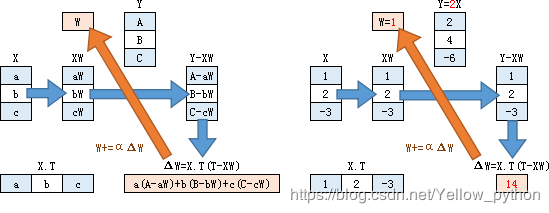
2.3、梯度上升
d = X.shape[1] # dimensionality
theta = np.mat([[1]] * d) # 初始化回归系数
for i in range(9, 9999):
alpha = 1 / i # 学习率(前期大步迭代,后期小步迭代)
h = sigmoid(X * theta)
theta = theta + alpha * X.transpose() * (y - h) # 最终梯度上升迭代公式
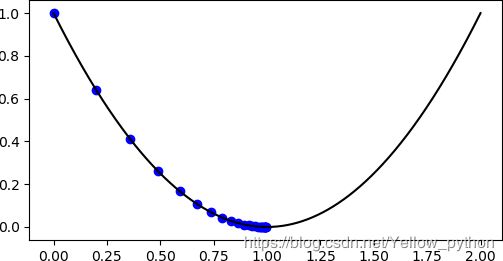
3、梯度下降原理
- 以 f ( x ) = x 2 − 2 x + 1 f(x)=x^2-2x+1 f(x)=x2−2x+1 为例,求函数的极值点
-
1、求导数:
f ′ ( x ) = 2 x − 2 f'(x)=2x-2 f′(x)=2x−2
2、计算机使用迭代的方法,一步一步逼近极值点
3、迭代公式: x i + 1 = x i − α ∂ f ( x i ) x i = x i − α ( 2 x i − 2 ) x_{i+1}=x_i-\alpha\frac{\partial f(x_i)}{x_i}=x_i-\alpha(2x_i-2) xi+1=xi−αxi∂f(xi)=xi−α(2xi−2)
import matplotlib.pyplot as mp, numpy as np
# 原函数
origin = lambda x: x ** 2 - 2 * x + 1
x = np.linspace(0, 2, 9999)
mp.plot(x, origin(x), c='black') # 绘制函数曲线
# 导数
derivative = lambda x: 2 * x - 2
# 梯度下降求极值点
extreme_point = 0 # 初始值
alpha = 0.1 # 步长,即学习速率
presision = 0.001 # 允许误差范围
error = np.inf # 初始化误差
while abs(error) >= presision: # 误差小于精度时退出迭代
mp.scatter(extreme_point, origin(extreme_point), c='b') # 绘制散点
error = alpha * derivative(extreme_point) # 步伐
extreme_point -= error # 梯度下降
mp.show() # 可视化
4、附录
| En | Cn |
|---|---|
| alpha | 希腊字母的第1个字母: α \alpha α |
| theta | 希腊字母的第8个字母: θ \theta θ |
| presision | 精度 |
| gradient ascent | 梯度上升 |
| linspace | abbr. 线性等分向量(linear space) |
| abbreviation | 缩写词 |
| shape | n. 形状;身材;v 形成 |
| extreme point | 极值点 |
| derivative | 导数 |
| partial derivatives | 偏导 |
import numpy as np, matplotlib.pyplot as mp
from sklearn.datasets import make_blobs
"""创建随机样本"""
X, Y = make_blobs(centers=2, cluster_std=5)
"""数据处理"""
X = np.insert(X, 0, 1, axis=1) # 增加一列,用于矩阵相乘
Y = Y.reshape(-1, 1)
x1, x2 = X[:, 1], X[:, 2]
fig, ax = mp.subplots() # 创建绘图对象
"""sigmoid函数"""
sigmoid = lambda x: 1 / (1 + np.exp(-x))
"""梯度上升"""
d = X.shape[1] # 维数
theta = np.mat([[1]] * d) # 初始化回归系数
for i in range(2000, 2200):
alpha = 1 / i # 步长(先大后小)
h = sigmoid(X * theta)
theta = theta + alpha * X.T * (Y - h) # 最终梯度上升迭代公式
"""数据可视化"""
ax.cla() # 清除
ax.axis([x1.min() + 1, x1.max() + 1, x2.min() + 1, x2.max() + 1])
ax.scatter(x1, x2, c=Y.reshape(-1)) # 原始样本点
x = np.array([x1.min(), x1.max()])
y = (-theta[0, 0] - theta[1, 0] * x) / theta[2, 0] # 决策边界
ax.plot(x, y)
mp.pause(.1)