【R的机器学习】模型性能提升探索：随机森林

基于上一节探索了调整决策树的参数进行优化，看到我们训练的模型具备更强的预测性：http://blog.csdn.net/yunru_yang/article/details/73873667

但是迄今为止，我们仍然是在决策树这个模型中进行优化，正如如果我们想跳的更高，更改了很多训练方式，可是我们的弹跳力仍然属于人的范畴；而我们想要有更大的飞跃，则需要做一个螳螂，在黑客帝国中，Neo被训练的就是在母体中，我们的思想禁锢了我们自己的潜能，而如何释放模型的潜能，当然就是从更大维度去探索，这一章介绍下决策树的升级版：随机森林。

顾名思义，森林应该就是很多树，所以随机森林也就是很多决策树的组合；还记得上一章进行了boosting算法的介绍，在这里再举一个通俗的例子：

一个简单的判断这个人是否有信用的决策树，遇到了一个小麻烦，因为每一次的分类，总有一些人分不干净，这个特征假设就是这个人的工资水平（假设银行只知道基本工资），因为在很多互联网公司中，有很多人不只有工资，还有股票（这个是隐含条件），但是银行不知道，所以隐隐感觉会有什么东西在工资背后作祟；那么基于此，对于那些工资低而且偿还能力好的用户（错误分类的对象），在迭代过程中提高这部分人的分类权重，我们看下，如果这个人的工资是1000元/月，理论上这个人是属于信用低下的用户，但是他每次都按期还贷，那么我们把这个人的分类权重调整更高，也就是默认了这个人是2000元/月的工资；在这里，我们看到boosting算法的一个优势：通过调整权重的方式进行了隐藏条件的过滤和预测。但是这是个串行方法：也就是说，我们只有先跑一次决策树，才能知道异常人在哪里，然后基于这个异常去调整权重。

而随机森林应用的方法主要是bagging，和boosting方法有点区别。关于这两个的区别，

http://blog.csdn.net/jlei_apple/article/details/8168856

这个博客已经说得非常明白，我再补充下，一般boosting方法应用的手段是gradient boosting，通俗来看就是这个权重赋值的大小是有一套规则的，而bagging方法比较简单，就是大家用投票的方式，比如三个决策树，第一个说这个条件信用高，第二个和第三个都说他信用低，那么这个人的信用就是低，这是一个并行方法，每个决策树都是独立的，不依赖其他决策树，也就是说，如果有三个人一起判断，boosting是第一个人判断完了，第二个人对第一个人修正，第三个人最后修正加审核，最后结果以第三个人最终审核完成为准–类似于工作流程；而bagging则更加民主，大家做同一件事，最后投票进行判断。

说了这么多，下面用R的决策树来模拟下随机森林，不是很准确，但是大概看到一个意思就可以。

随机森林一般情况下对于变量不会取完整的，经验上每一个决策树都是取sqrt(m)个特征，比如iris数据集有四个特征，那么每一个决策树取两个特征进行训练；而数据是有放回抽样，抽不中的理论上作为测试集。

set.seed(1234)
rn<-sample(nrow(iris),nrow(iris),replace=T)
train_1<-iris[rn,c(1:2,5)]
train_2<-iris[rn,c(2:3,5)]
train_3<-iris[rn,c(3:4,5)]
train_4<-iris[rn,c(1,3,5)]
train_5<-iris[rn,c(2,4,5)]
train_6<-iris[rn,c(1,4,5)]
test<-iris[-rn,]
m1<-C5.0(Species~.,data=train_1)
m2<-C5.0(Species~.,data=train_2)
m3<-C5.0(Species~.,data=train_3)
m4<-C5.0(Species~.,data=train_4)
m5<-C5.0(Species~.,data=train_5)
m6<-C5.0(Species~.,data=train_6)
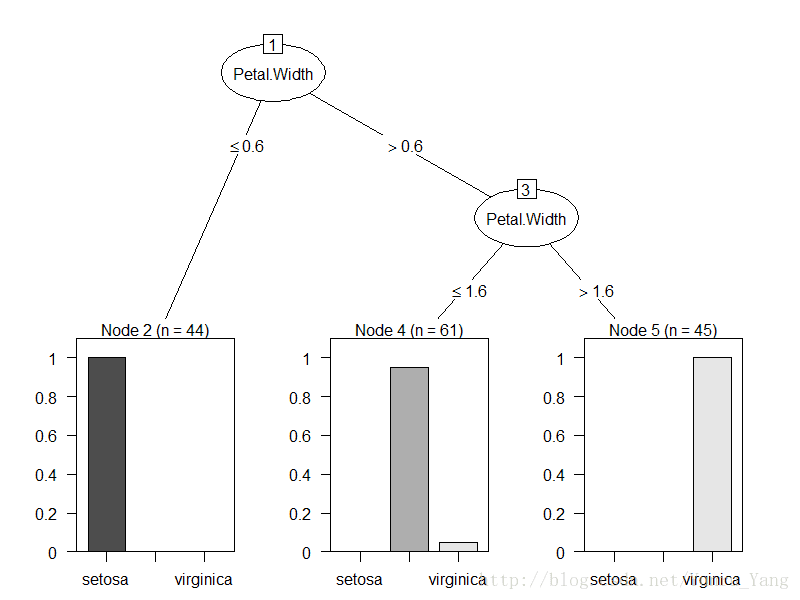
plot(m1)
plot(m2)
plot(m3)
plot(m4)
plot(m5)
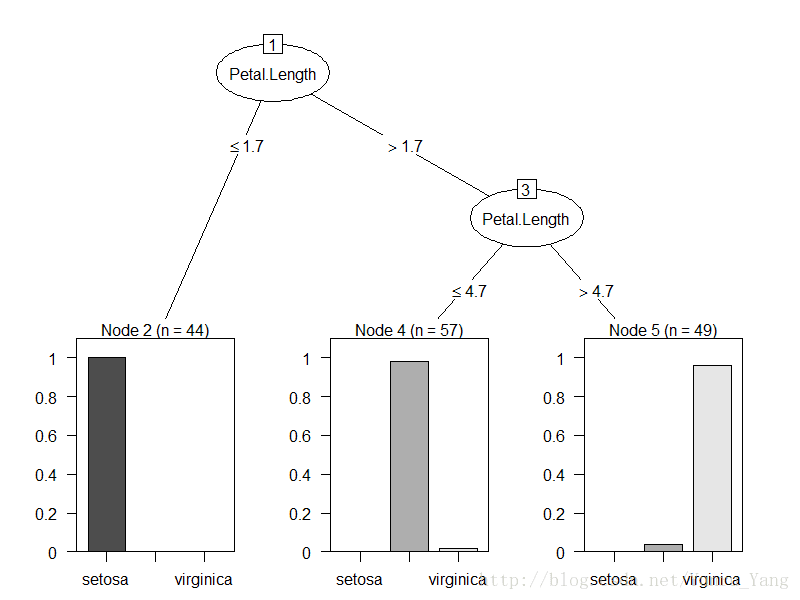
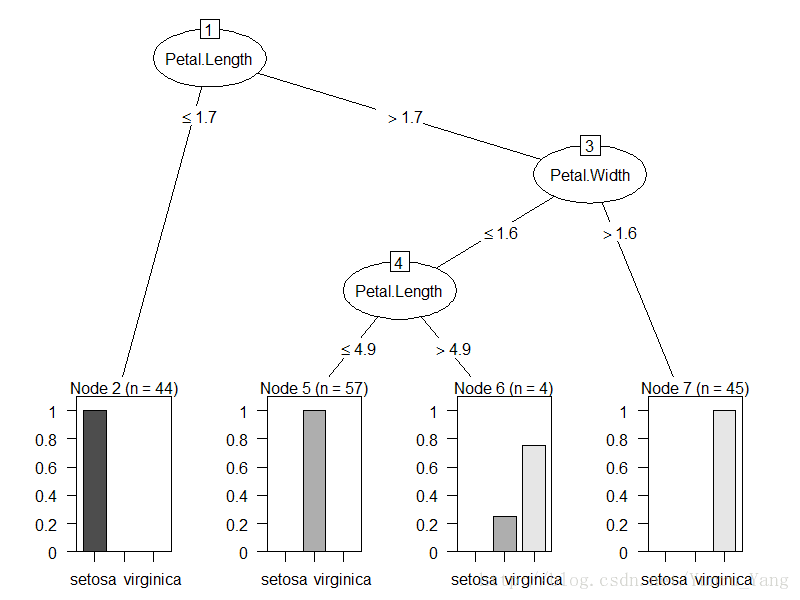
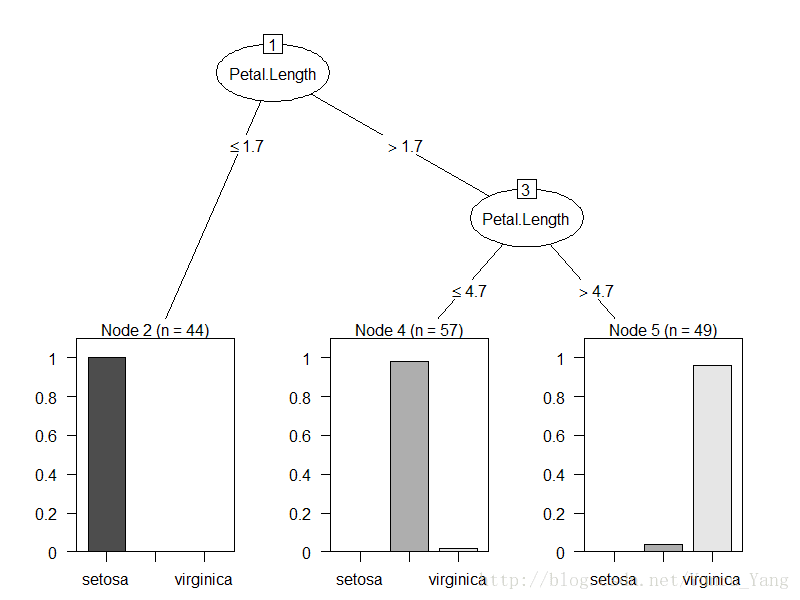
plot(m6)

Iirs数据集除了species（作为结果），特征一共有四个，如果按照每一次都是2个特征的话，一共需要有C4,2,=6种方式遍历，所以以上就是6棵决策树，而rn就是有放回抽样的行。

我们看下这六个图片加以说明：

OK,其实看到这六个决策树的分类都不是那么干净，但是用来投票是不是好一点呢？我们随便取一个test数据：

 Sepal.Length Sepal.Width Petal.Length Petal.Width Species
2          4.9           3          1.4         0.2  setosa

先看下这个在我们六棵决策树中的结果是什么：

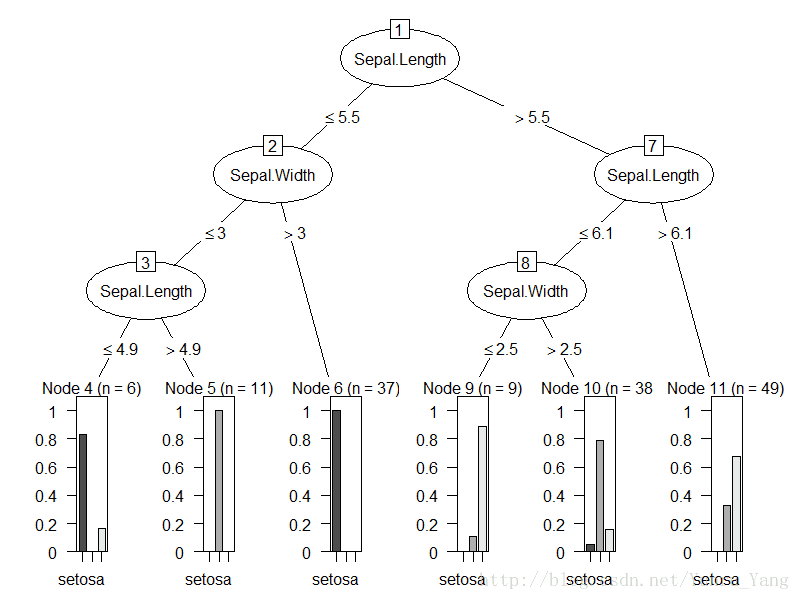
第一棵树，如果Sepal.Length=2<=5.5，进入左边分支，然后Sepal.Width=3<=3,再进入左边，然后Sepal.Length=2<=4.9，结果是setosa;

同理，第二棵树是setosa，第三棵树是setosa，第四棵树是setosa，第五棵树是setosa，第六课树是setosa，这个结果也是比较尴尬，本来以为可以有不同的意见，但是大家一致认为这个结果是setosa，一个6:0的投票，我们的模型预测就是setosa，而test中的结果就是setosa，这个比较准确了就。

当然，R中的随机森林不会这么复杂，手工去设定决策树，R中有个专门的randomforest函数，用来重复模拟决策树，提高准确性。

library(randomForest)
m_rf<-randomForest(Species~.,data=iris,ntree=500)

其中ntree的参数是决策树的个数，默认是500棵数，也不用调整。

而在之前的模型中，我们已经介绍过了，随机森林是有放回抽样，那么总有一些数据是抽取不到的，这些数据就作为了我们的测试集，所以这个模型自带评价属性：

Call:
 randomForest(formula = Species ~ ., data = iris, ntree = 500) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 2

        OOB estimate of  error rate: 4%
Confusion matrix:
           setosa versicolor virginica class.error
setosa         50          0         0        0.00
versicolor      0         47         3        0.06
virginica       0          3        47        0.06

下面的混淆矩阵，我们看到准确率是对角线的(50+47+47)/150=0.96，准确率达到96%，而

OOB estimate of  error rate: 4%

表明OOB（out-of-bag）率有4%，关于OOB，这篇文章翻译了stackflow的一篇回答，说的还是比较通俗易懂

http://blog.sina.com.cn/s/blog_4c9dc2a10102vl24.html

简单来说，因为我们的随机森林是随机抽样，并且基于没有抽到的数据作为测试集用来测试那些训练集，所以，这个出包错误率，可以理解成我们对于测试的准确率，一般这个OOB是4%，那么准确率大致上会是1-4%=96%，和我们看到的一致

基于此我们用了一个最简单的模型，但是还记得上一章说的caret函数么？可以对比一个模型中不同参数，而随机森林的参数选择，以及抽样的方式会影响到最终的模型准确度。

1、随机森林的特征参数选择
我们之前的决策树模拟随机森林，一般经验上都是用总体参数的平方根作为每个决策树的参数输入，那么既然对比森林的好坏，我们可以调整每个树的大小；

library(caret)
m_rf_im<-train(Species~.,data=iris,method='rf',metric='Kappa',
               tuneGrid=data.frame(.mtry=c(2,4,6,8)))

里面的metric=’Kappa’是输出带kappa值的结果，而tuneGrid是针对.mtry为2,4,6,8分别作为特征值迭代。

看下结果：

Random Forest 

150 samples
  4 predictor
  3 classes: 'setosa', 'versicolor', 'virginica' 

No pre-processing
Resampling: Bootstrapped (25 reps) 
Summary of sample sizes: 150, 150, 150, 150, 150, 150, ... 
Resampling results across tuning parameters:

  mtry  Accuracy   Kappa    
  2     0.9506443  0.9250162
  4     0.9503024  0.9245781
  6     0.9495181  0.9233774
  8     0.9480401  0.9211162

Kappa was used to select the optimal model using 
 the largest value.
The final value used for the model was mtry = 2.

不同的mtry的准确度差不多，反而是越小的越高，顺便说一句，如果mtry=8，也就是所有的参数作为一个树，那么和普通的决策树bagging方法是一样的，当参数越多，随机森林越收敛成决策树。

最后一行是推荐的mtry=2，和我们之前的默认参数一致；

2、 尝试次数
除了我们的参数的特征值选择，还有一个参数是类似之前决策树说的抽样次数，还记得之前我们说的，随机森林是进行有放回的随机抽样么？但是不管树多么多，抽样方式都是一种。

这块我们可以升级下抽样方式，从之前的随机有放回抽样，升级到多次有放回抽样，一个通常的方法是10折CV。

既然说到了这，除了简单的随机抽样，有其他两类常用抽样方式：

holdout：也叫保持法；把数据分成三份，第一份是训练集，第二份是验证数据集，第三个是测试集；模型由训练集训练，然后通过验证数据集进行评估和迭代，然后最后做测试

K-fold cross-validation：针对数据分成K份，每个数据中90%作为训练集，10%作为测试集，一般K=10，也就是10-cross-validation，即10折CV。

OK，那我们改进下抽样方案：

library(caret)
ctrl <- trainControl(method = "repeatedcv",
                    number = 10, repeats = 10) 
m_rf_im2<-train(Species~.,data=iris,method='rf',metric='Kappa',
                trControl=ctrl,
               tuneGrid=data.frame(.mtry=c(2,4,6,8)))

我们的结果是：

Random Forest 

150 samples
  4 predictor
  3 classes: 'setosa', 'versicolor', 'virginica' 

No pre-processing
Resampling: Cross-Validated (10 fold, repeated 10 times) 
Summary of sample sizes: 135, 135, 135, 135, 135, 135, ... 
Resampling results across tuning parameters:

  mtry  Accuracy   Kappa
  2     0.9526667  0.929
  4     0.9506667  0.926
  6     0.9520000  0.928
  8     0.9533333  0.930

Kappa was used to select the optimal model using 
 the largest value.
The final value used for the model was mtry = 8.

竟然又回来了。。推荐我们用mtry=8，也就是决策树的10折CV，Kappa值是0.93，准确率为95.3%；基本和上一章持平。

后续看看其他模型有没有更好的预测。