编译原理学习笔记之词法分析中的状态机与自动机

有限状态机

关于词法记号的识别可以用有限状态机来描述

有限状态机以转化图的形式描述状态的转化

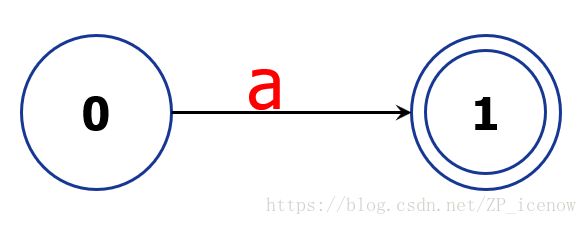
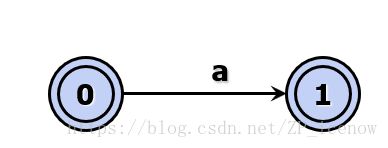
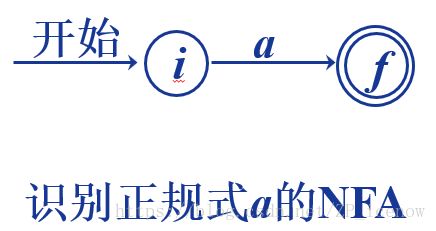
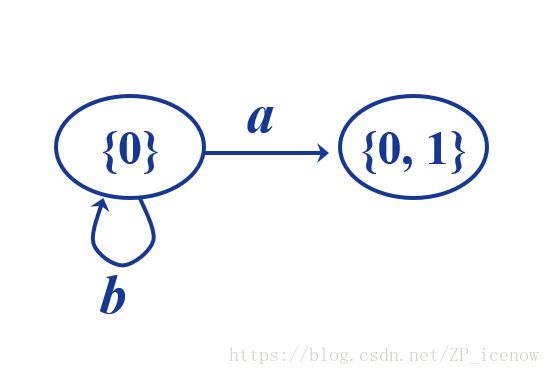
比如对于正规式d->a

其中初始状态为0，匹配到a之后，到达状态1，1的双圈表示最终状态；类似地

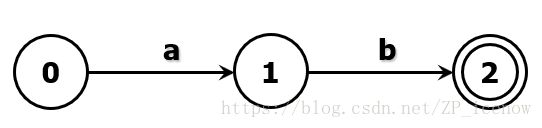
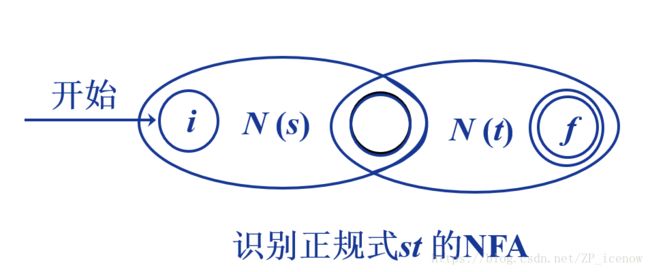
正规式d->ab

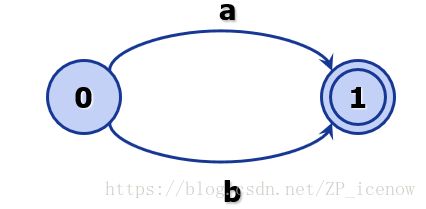
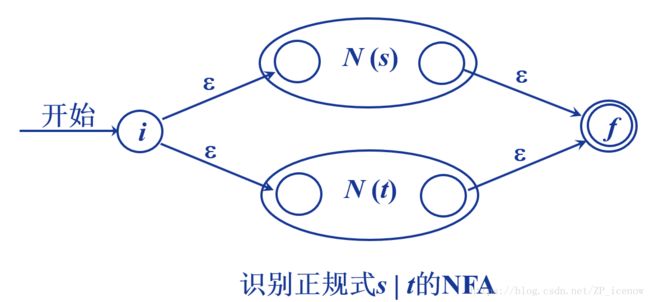
正规式d->a|b

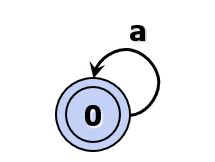
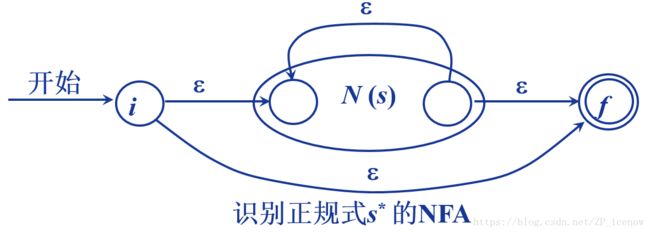
正规式d->a*

该状态表示可以匹配零个a到达最终状态0，也可以匹配无数个a到达最终状态0

正规式d->a?

表示a出现0次或1次，因此有两个最终状态

因此我们可以将独立地正规式加以组合处理来解决复杂的正规式

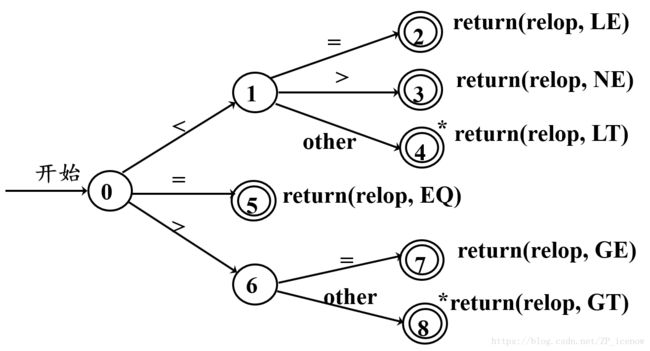
比如对关系运算符的匹配

其中诸如 *return...的结果表示指针回退一位，吐出多读入的other字符

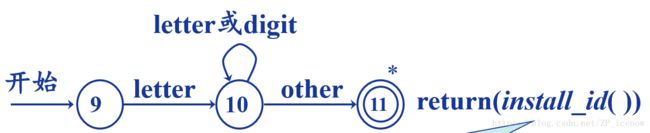
再比如标识符的匹配id ->letter (letter | digit )*

其中匹配过程可以概括为三步

• 检查关键字表，如果在表中发现该词法单元则返回相应的记号并退出，否则转向2

• 该词法单元是标识符，在符号表中查找，若找到该词法单元则返回该条目的指针并退出，否则执行3

• 在符号表中建立一个新的条目，把该词法单元填入，并返回此新条目的指针

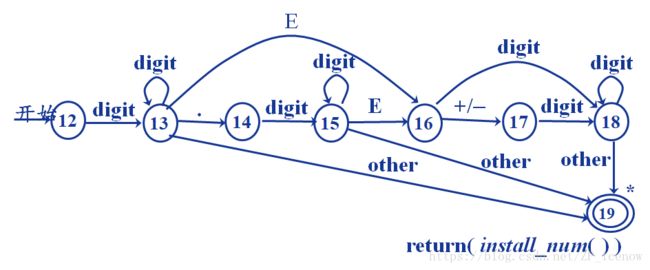
对于无符号数num ->digit+ (.digit+)? (E (+ | -)? digit+)?

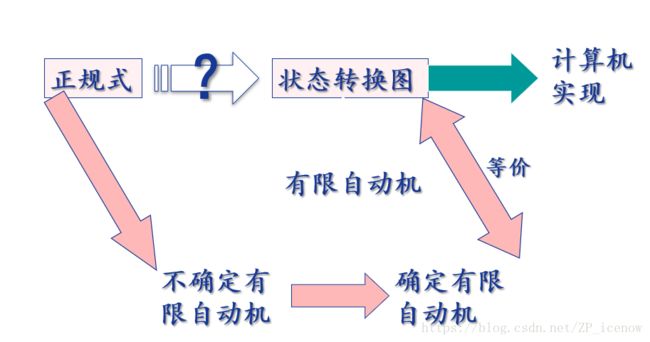
这个就稍微有点复杂了，因此直接通过正规式有些很难写出状态转化图，因此我们需要借助中间手段来实现这一过程

一般的流程如下图所示

因此我们引入有限自动机的概念

在编程中，我们提到的自动机，状态机之类的一般都指一种程序

识别器：是一个程序，取串x作为输入，当x是语言的句子时，它回答“是”，否则回答“不是”

确定有限自动机（Deterministic Finite Automata，DFA）

DFA是这样一个数学模型，包括

• 状态集合S
• 输入字母表Σ
• 转换函数move：S x Σ ->S
• 唯一的初态s∈S
• 终态集合F 包含于 S 

不确定的有限自动机（Non-Deterministic Finite Automata，NFA）

NFA是这样一个数学模型，包括

• 状态集合S
• 输入字母表Σ
• 转换函数move：
• 唯一的初态s∈S
• 终态集合F 包含于 S

不难发现，DFA和NFA的主要区别就在于转换函数的入口，NFA的输入字符包括ε，另外NFA一个状态对于某个字符可能有多条输出边，这也是NFA的缺点，计算机当然不具备人脑的联想判断功能，因此对于所有的输入必须要求是确定状态的，因此NFA只是我们推出DFA的一个中间过程。

NFA与DFA的区别

• NFA中允许ε转换边，而DFA不允许
• NFA的move（s，a）可以是一个多元集合，而DFA中的move（s，a）最多有一个元素

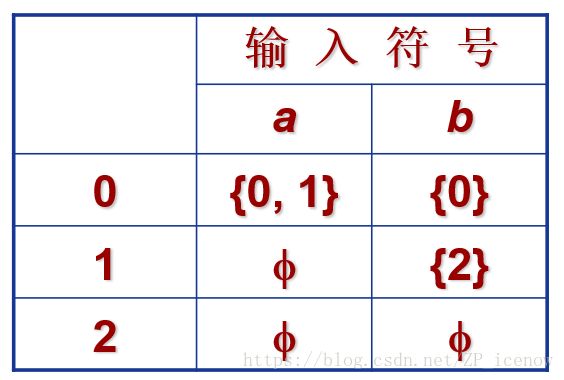
由于计算机对图不具有直接识别能力，因此我们引入状态迁移表 的形式

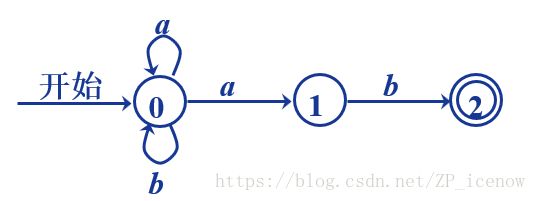
比如对于(a|b)*ab NFA为

对应的状态迁移表为：

• 优点：快速定位
• 缺点：字母表过大，或大部分转换状态为空集时浪费空间

DFA的构建

途径1.自然语言描述-》DFA

比如识别S ={0,1}上能被能5整除的二进制数

方法

• 首先列出全部的可能状态
• 从各个状态出发构造边及输入记号

途径2.正规式-》DFA

比如上面提到的关系运算符的识别，就可以直接根据正规式画出DFA

途径3.正规式-》NFA-》DFA

• 先构建NFA
• NFA-》DFA（子集构造法）
• DFA化简

①.先构建NFA

首先拆分成独立地正规式结构

、

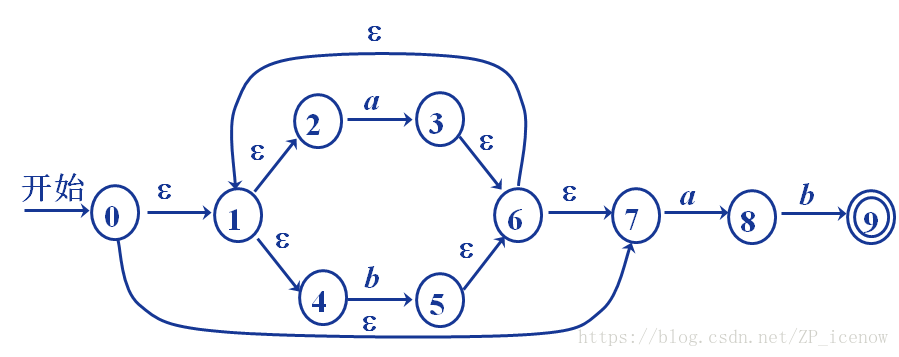
这样，对于(a|b)*ab => NFA，即为：

 

以上，我们完成了第一步，即正规式-》NFA，然后进入第二步

②.NFA->DFA

理论依据：根据有限自动机理论，设L为一个有不确定的有限自动机接受的集合，则存在一个接受L的确定的有限自动机

简单点说就是对于任一个NFA，都能找到与之对应的DFA，这也是我们转化的前提

转换过程运用子集构造法

• DFA的一个状态是NFA的一个状态集合
• 读了输入a1 a2 … an后，NFA能到达的所有状态：s1, s2, …,  sk， 则DFA到达状态{s1, s2, …,  sk}

简单点可以理解为DFA将NFA能够到达的状态集合视作一个状态

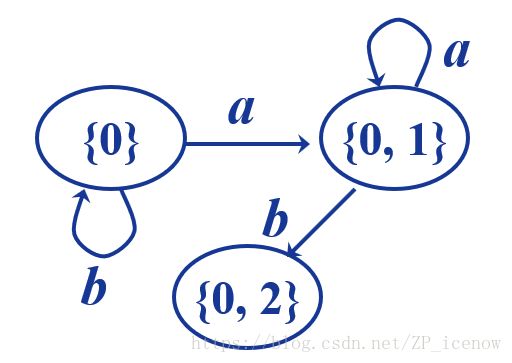
还是以(a|b)*ab 为例，对应右侧的NFA，我们将其转换为DFA

 

首先初始状态为0没什么好说的，NFA（图右侧）中0状态经过a可以到达0状态或者1状态，因此DFA的状态即是这两个状态的集合，如图左，同理我们接下来画出0状态经过b到达的状态(集)如下

同理，我们找到{0，1}这个DFA状态经过a，b到达的状态，其中0 --a-> 0/1, 1不经过a，所以{0，1}经过a还是可以到达0，1，同理，0--b-> 0； 1 --b-> 2,所以{0，1}经过b可以到达的状态是0，2，写成集合，另外因为2是接受状态(最终状态),所以含有2的DFA状态集应该也为接受状态，所以要化成同心圆，下图中应该是同心圆

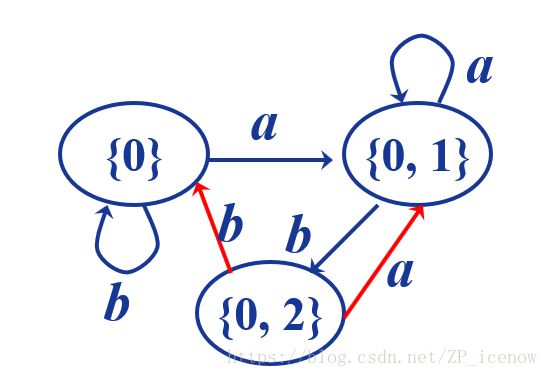
同理我们再找出{0，2}这个DFA状态经过a，b到达的状态

就是这样

同样如果是过程化的状态机图，即下面这种形式

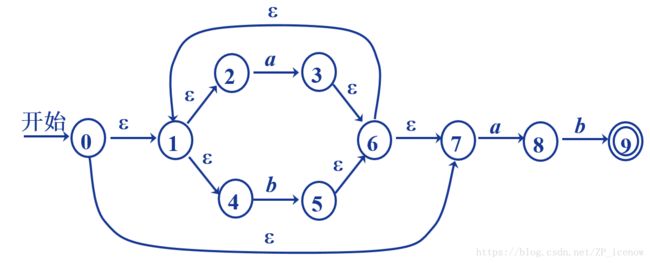
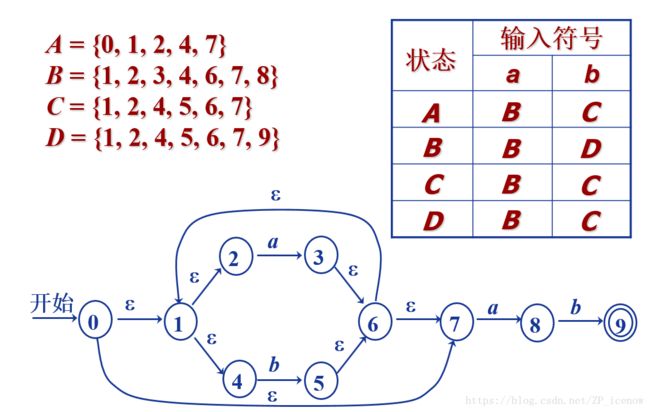
也是按照同样的步骤，其中，经过空串到达的状态全部等价，即初始状态应该为{0，1，2，4，7}，我们用A表示

随即就是找A状态经过a，b能够到达的状态，包括经过空串等价的状态，得到B={1，2，3，4，6，7，8}，C={1，2，4，5，6，7}

以此类推，顺便引入状态迁移表（方便下一步骤），结果如下

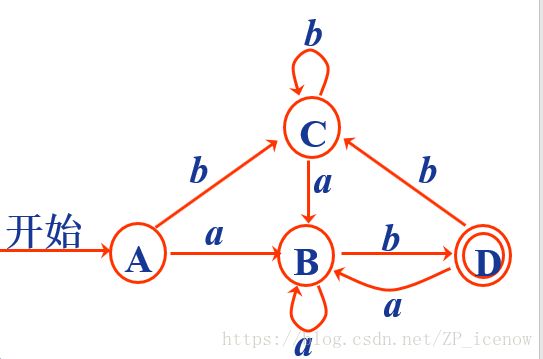
最后根据状态迁移表，我们画出对应的DFA，如下

 

那么问题来了，这种形式的DFA是不是最终的形式呢，接下来就是我们的第三步

③.DFA化简

其实对于一个正规式，DFA可以有很多种，但是只有一种是最简的，我们知道，计算机是不能够判断模棱两可的东西，因此我们必须给出唯一的标准，也就是唯一的最简式

那么如何判断一个DFA是不是最简的呢？我们引入以下概念

状态的可区分性：存在串w，使得从状态s开始，对w进行状态转换，最终停在某个接受状态；而对于从t开始对w进行状态转换后，却停在某个非接受状态

关于接受状态和非接受状态上面有渗透该知识，接受状态就是最终状态，即输入的串满足该正规式的要求，该正规式接受这一输入串，不满足要求就是不接受啦~所以上面的概念我们举个例子理解一下

比如在上一个图中，对于A，C两个状态，经过a，二者都到达B状态，经过b，二者都到达C状态，反应完全一致，我们即判定A，C两个状态不可区分；对于A，B两个状态，A状态经过a到达B状态，B状态经过a同样到达b状态，但是A状态经过b状态到达C状态，而B‘状态经过b状态到达D状态，D状态即是接受状态，满足可区分性的判定，因此A，B状态在b上可区分

如果两个状态不可区分，即对任何输入串的反应一致，那么显然，这两个状态应该是一致的，即我们可以合并不可区分的状态

DFA化简途径：

• 根据状态是否可以区分，将状态划分成若干个集合，每个集合内的状态之间都不可区分，而任意两个集合中的元素都是可以互相区分的
• 依据原始的DFA，在合并后的状态基础上，建立新的状态转换关系

化简时DFA的状态转换函数必须是一个全函数

（全函数：对于所有的输入都有对应的边，比如有a，b两个输入，那么每个状态必须有a，b两个出边，否则称之为部分函数

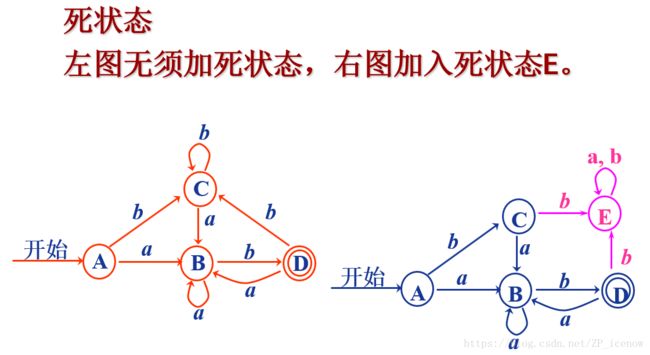
部分函数需要添加死状态变成全函数，死状态即是添加一个状态，使所有缺失的边都指向它，它自己的所有输出边也指向本身，如下图

 

首先将接受状态和非接受状态分为两个部分

{A, B, C}, {D}

对于非接受状态，判断其转换函数

move({A, B, C}, a} = {B}             ---------->   结果还是非接受状态

move({A, B, C}, b} = {C, D}        ------------>  结果出现接受状态，而这种改变是由于状态B造成，因此将B拆分出来

{A, C}, {B}, {D}

重复以上过程

move({A, C}, a} = {B}

move({A, C}, b} = {C}

发现A，C不存在例外了

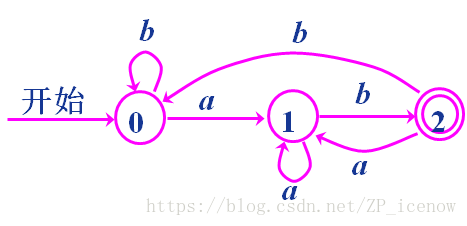
为格式化，我们将字母变成数字表示，将A。C合并

则有

这就是最终结果

 

 

以上，转换的全部过程，至此，状态机和自动机的部分也全部结束