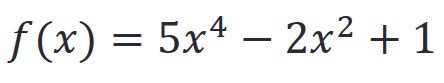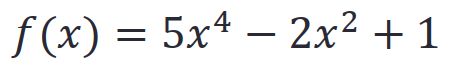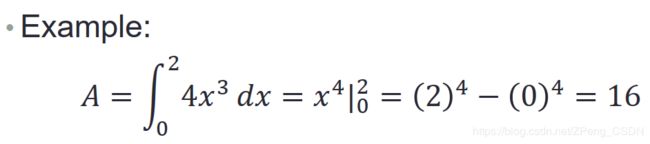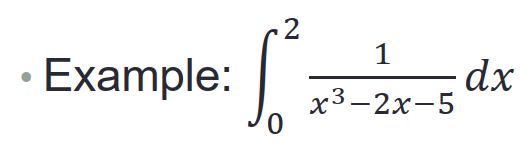MATLAB学习笔记——数值微积分
前言
本次主要是为了记录下学习和复习MATLAB中的知识点，顺便复习一波高数，以此来巩固一下自己薄弱的知识体系，MATLAB前面基础零散的小知识点就暂时先不管，事先声明，本人是跟着的B站上的教程视频 MATLAB教程_台大郭彦甫（14课）原视频补档，所以博客中的大部分案例也都来自郭老师得教案。
基础必知
公式：
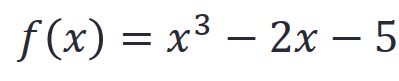
在MATLAB中用p = [1 0 -2 -5];表示，所在位置为变量指数。
多项式微分公式：
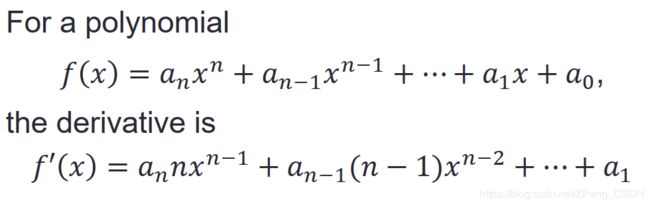
多项式积分公式：
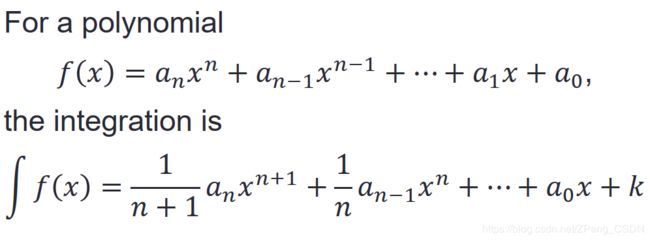
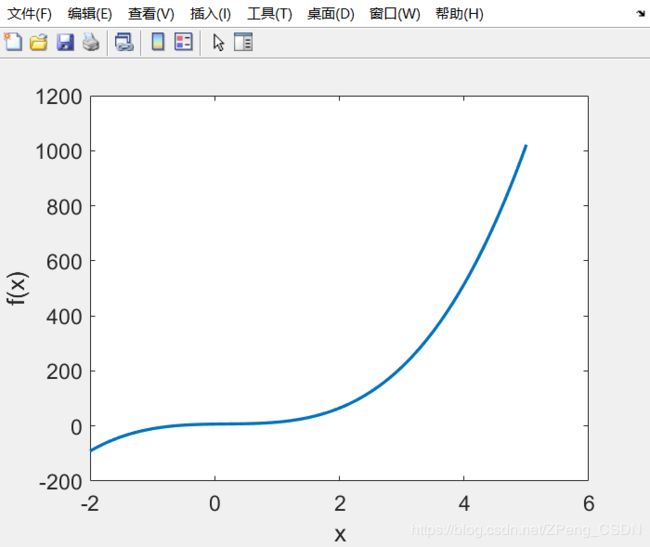
多项式计算
a = [9,-5,3,7]; x = -2:0.01:5;
f = polyval(a,x);
plot(x,f,'LineWidth', 2);
xlabel('x'); ylabel('f(x)');
set(gca, 'FontSize', 14)
polyval - 多项式计算
此 MATLAB 函数 计算多项式 p 在 x 的每个点处的值。参数 p 是长度为 n+1 的向量，其元素是 n 次多项式的系数（降幂排序）。
多项式微分
p=[5 0 -2 0 1];
polyder(p)
polyder - 多项式微分
此 MATLAB 函数 返回 p 中的系数表示的多项式的导数。
计算微分后某个点的值。
polyval(polyder(p),7)
多项式积分
p=[5 0 -2 0 1];
polyint(p, 3)
polyint - 多项式积分
此 MATLAB 函数 使用积分常量 k 返回 p 中系数所表示的多项式积分。
计算积分后某个点的值。
polyval(polyint(p, 3),7)
函数求导
x = [1 2 5 2 1];
diff(x)
diff - 差分和近似导数
此 MATLAB 函数 计算沿大小不等于 1 的第一个数组维度的 X 相邻元素之间的差分。
可以看出得到的结果为每个数之间的间隔。
求两点之间的斜率
x = [1 2]; y = [5 7];
slope = diff(y)./diff(x)
特定区间内求导
h = 0.5; x = 0:h:2*pi;
y = sin(x); m = diff(y)./diff(x);
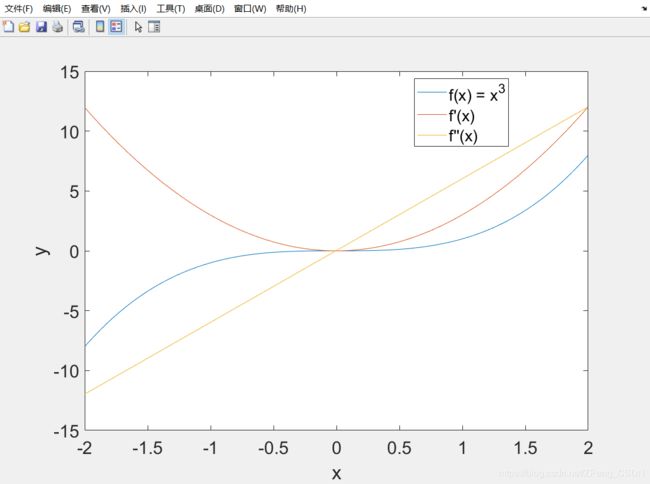
二次求导与三次求导
x = -2:0.005:2; y = x.^3;
m = diff(y)./diff(x);
m2 = diff(m)./diff(x(1:end-1));
plot(x,y,x(1:end-1),m,x(1:end-2),m2);
xlabel('x', 'FontSize', 18);
ylabel('y', 'FontSize', 18);
legend('f(x) = x^3','f''(x)','f''''(x)');
set(gca, 'FontSize', 18);
end - 1是因为每次求导后区间都会缩小1。
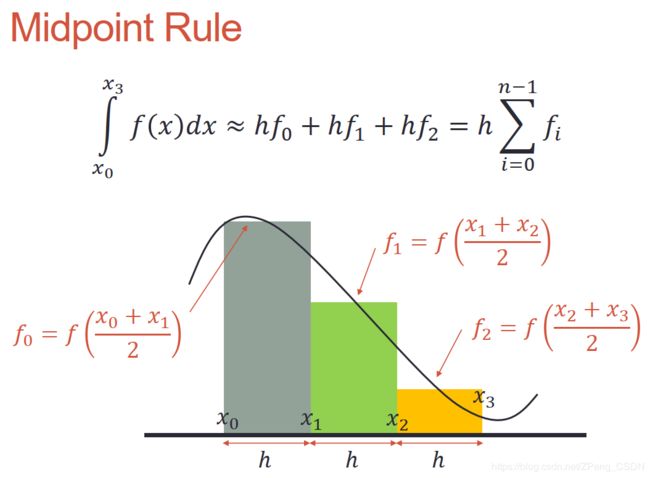
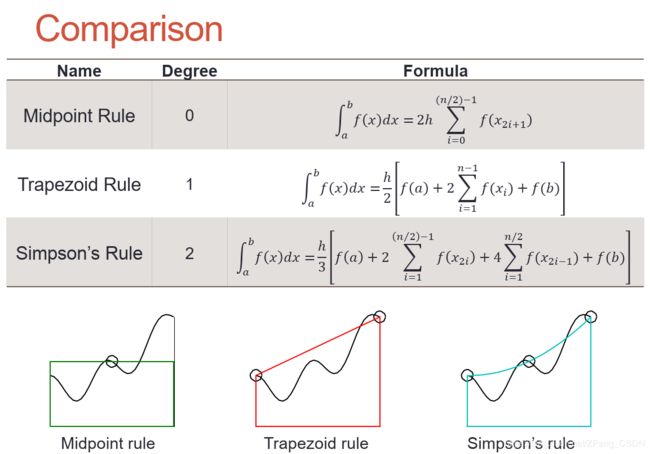
中点法则（Midpoint Rule）
使用Midpoint Rule来求积分的区间面积。
h = 0.05; x = 0:h:2;
midpoint = (x(1:end-1)+x(2:end))./2;
y = 4*midpoint.^3;
s = sum(h*y)
midpoint - Midpoint weight initialization function
This MATLAB function takes two arguments, Number of rows (neurons) R-by-Q matrix of input value ranges = [Pmin Pmax]
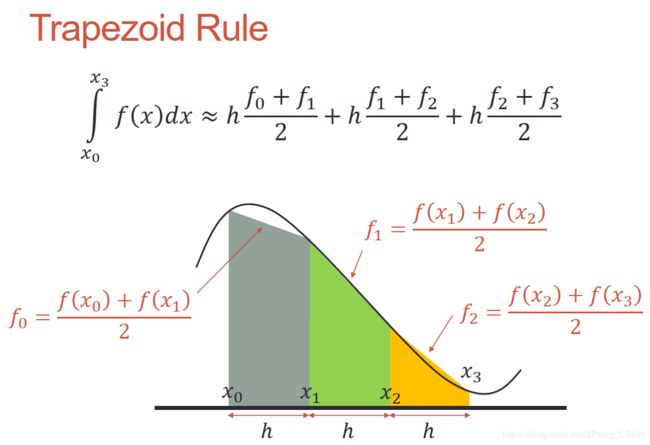
梯形法则（Trapezoid Rule）
使用Trapezoid Rule来求积分区间面积。
h = 0.05; x = 0:h:2; y = 4*x.^3;
s = h*trapz(y)
trapz - 梯形数值积分
此 MATLAB 函数 通过梯形法计算 Y 的近似积分（采用单位间距）。Y 的大小确定求积分所沿用的维度：
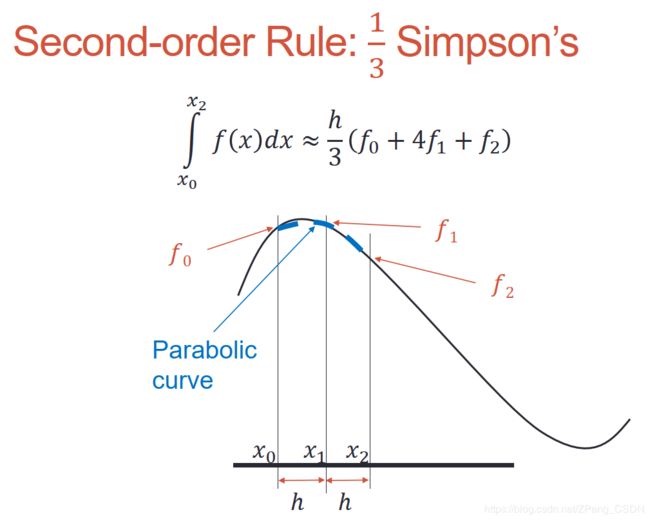
二阶规则（Second-order Rule）
使用Second-order Rule计算积分区间面积。
h = 0.05; x = 0:h:2; y = 4*x.^3;
s = h/3*(y(1)+2*sum(y(3:2:end-2))+...
4*sum(y(2:2:end))+y(end))
三者比较
回到最简单的方法（Function Handles (@) ）
求积分
y = @(x) 1./(x.^3-2*x-5);
integral(y,0,2)
多重积分
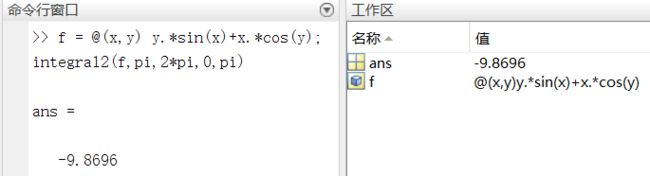
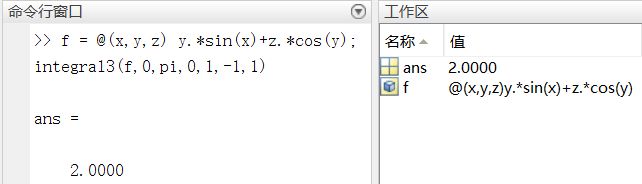
二重积分
f = @(x,y) y.*sin(x)+x.*cos(y);
integral2(f,pi,2*pi,0,pi)
三重积分
f = @(x,y,z) y.*sin(x)+z.*cos(y);
integral3(f,0,pi,0,1,-1,1)
