【笔试】【python】【每天10道代码笔试题】数据结构与算法-刷题
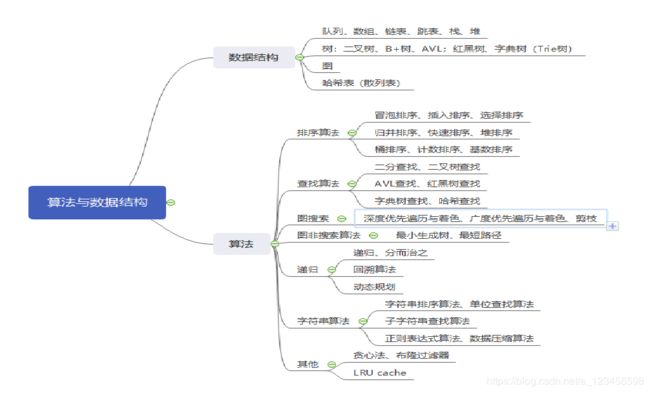
数据结构与算法框架:
1.
while True:
try:
do something
except:
breakwhile True 必须和break结合,无异常时执行try,异常时执行except,break退出循环。
2.raw_input()与input()
python2
存在raw_input()和input()两个函数
raw_input()将所有输入作为字符串看待,并且返回字符串类型
input()只用于数字的输入,返回所输入数字类型
python3
只存在input()函数,接收任意类型的输入,并且将输入默认为字符串类型处理,返回字符串类
3.赋值a=b,开辟新地址,b变化不会影响a。
(1)不可变对象(数字、字符串、元组),可变对象(列表、字典、集合)
(可变/不可变 分析的是 ‘=’情形下的地址。)
不可变对象:存放在地址中的值不会被改变,对象改变时会开辟新地址。
可变对象:存放在地址中的值会原地改变,对象改变时不会开辟新地址。
(2)python赋值、深拷贝和浅拷贝的区别:
(深、浅拷贝分析的是可变对象情形下的的地址)
对于可变类型 List、Dictionary、Set,举例:列表alist和a:
1)赋值:改变alist,a作相同变化,地址均不变。
2)copy.copy( )浅拷贝: 变量开辟新地址,元素地址不变。
3)copy.deepcopy( )深拷贝:变量和元素都开辟新地址。
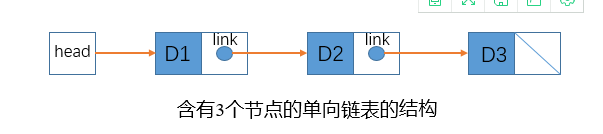
4.链表
单向链表节点的表示:
class Node(object):
'''定义单链表节点类'''
def __init__(self,data,next = None):
'''data为数据项,next为下一节点的链接,初始化节点默认链接为None'''
self.data = data
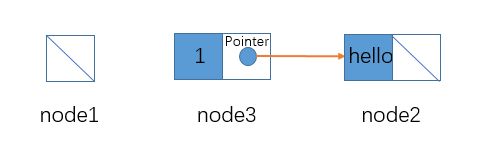
self.next = next节点实例化:
# 定义3个节点对象分别为node1、node2和node3
node1 = None
node2 = Node(1,None)
node3 = Node('hello',node2)
print(node1,node2.data,node2,node3.next)![]()
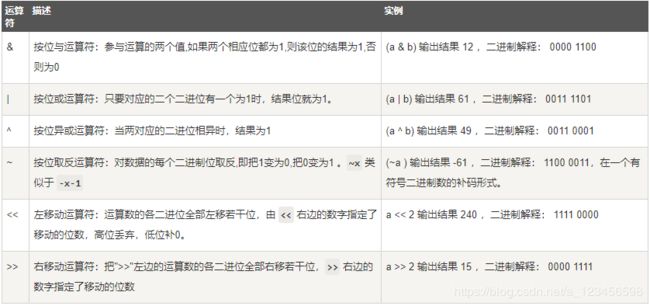
5.位运算:
n小于0时,用补码表示:
if n < 0:
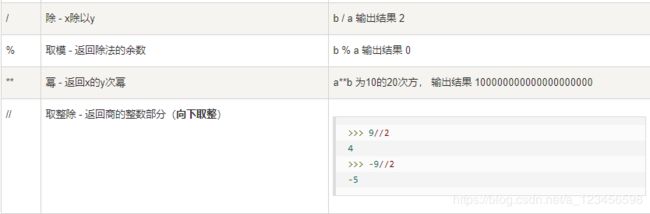
n = n & 0xffffffff6.算数运算符:
注意:python3中, / 返回float,// 返回int
7.python3中,range()用法和列表切片经常搞混:
(1)range()返回的不是列表,而是一个包含索引的对象:
range()是一个函数,用的是括号和逗号。
for i in range(n): #顺着取索引,0~n-1
for i in range(n-1,-1,-1) #倒着取索引,n-1~0(2)列表切片:
切片是取列表,用的是中括号和冒号。
list = [1, 2, 3, 4, 5, 6, 7 ]
list2[1:5]: [2, 3, 4, 5]
8.用sys模块输入:
import sys(1)控制台单个数字输入
a=int(sys.stdin.readline().strip())(2)把这一行用空格分开的数字,变为列表
b=list(map(int,sys.stdin.readline().strip().split()))(3)指定行数 输入多行数据 返回二维list
c=[]
for i in range(a):
cc=list(map(int,sys.stdin.readline().strip().split()))
c.append(cc)
print(c)
(4)不指定行数 输入多行数据 返回二维list:
d=[]
while True:
try:
dd=list(map(int,sys.stdin.readline().strip().split()))
if not dd:
break
d.append(dd)
except:
break
print(d)9.子结构和子树的区别:
子树的意思是:
包含了一个结点,就得包含这个结点下的所有节点,一棵大小为n的二叉树有n个子树,就是分别以每个结点为根的子树。
子结构的意思是:
包含了一个结点,可以只取左子树或者右子树,或者都不取。
10、列表:
.append(a) #在末尾加上元素a
.pop() #删除末尾元素
.extend([1,2]) #加入新列表
#列表删除元素还可以进行切片操作。
11.空列表[ ]、数字0、关键字None
都是代表否的意思。
12.图:深度优先遍历(DFS)、广度优先遍历(BFS)
DFS:对于树来说,是前序遍历。沿着一条路一直走到底,然后进行回溯
BFS:对于树来说,是层级遍历。优先搜索所有相邻的节点,再访问所有相邻节点的邻节点。
(1)树的BFS、DFS:
# 定义节点类
class Node(object):
def __init__(self,val,left=None,right=None):
self.val = val
self.left = left
self.right = right
# 创建树模型
node = Node("A",Node("B",Node("D"),Node("E")),Node("C",Node("F"),Node("G")))
def BFS(root):
# 使用列表作为队列,pop(0)
queue = []
# 将首个根节点添加到队列中
queue.append(root)
# 当队列不为空时进行遍历
while queue:
# 从队列头部取出一个节点并判断其是否有左右节点
# 若有子节点则把对应子节点添加到队列中,且优先判断左节点
temp = queue.pop(0)
left = temp.left
right = temp.right
if left:
queue.append(left)
if right:
queue.append(right)
print(temp.val,end=" ")
def DFS(root):
# 使用列表作为栈,pop()
stack = []
# 将首个根节点添加到栈中
stack.append(root)
# 当栈不为空时进行遍历
while stack:
# 从栈的末尾弹出一个节点并判断其是否有左右节点
# 若有子节点则把对应子节点压入栈中,且优先判断右节点
temp = stack.pop()
left = temp.left
right = temp.right
if right:
stack.append(right)
if left:
stack.append(left)
print(temp.val,end=" ")
print("BFS",end=" ")
BFS(node)
print("")
print("DFS",end=" ")
DFS(node)
BFS A B C D E F G
DFS A B D E C F G
(2)图的BFS、DFS:
# 定义图结构
graph = {
"A": ["B","C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D","E"],
"D": ["B", "C", "E","F"],
"E": ["C", "D"],
"F": ["D"],
}
def BFS(graph,vertex):
# 使用列表作为队列
queue = []
# 将首个节点添加到队列中
queue.append(vertex)
# 使用集合来存放已访问过的节点
looked = set()
# 将首个节点添加到集合中表示已访问
looked.add(vertex)
# 当队列不为空时进行遍历
while(len(queue)>0):
# 从队列头部取出一个节点并查询该节点的相邻节点
temp = queue.pop(0)
nodes = graph[temp]
# 遍历该节点的所有相邻节点
for w in nodes:
# 判断节点是否存在于已访问集合中,即是否已被访问过
if w not in looked:
# 若未被访问,则添加到队列中,同时添加到已访问集合中,表示已被访问
queue.append(w)
looked.add(w)
print(temp,end=' ')
def DFS(graph,vertex):
# 使用列表作为栈
stack = []
# 将首个元素添加到队列中
stack.append(vertex)
# 使用集合来存放已访问过的节点
looked = set()
# 将首个节点添加到集合中表示已访问
looked.add(vertex)
# 当队列不为空时进行遍历
while len(stack)>0:
# 从栈尾取出一个节点并查询该节点的相邻节点
temp = stack.pop()
nodes = graph[temp]
# 遍历该节点的所有相邻节点
for w in nodes:
# 判断节点是否存在于已访问集合中,即是否已被访问过
if w not in looked:
# 若未被访问,则添加到栈中,同时添加到已访问集合中,表示已被访问
stack.append(w)
looked.add(w)
print(temp,end=' ')
# 由于无向图无根节点,则需要手动传入首个节点,此处以"A"为例
print("BFS",end=" ")
BFS(graph,"A")
print("")
print("DFS",end=" ")
DFS(graph,"A")
BFS A B C D E F
DFS A C E D F B
13.
树节点类、
二叉树类(包括前、中、后序遍历)、
二叉树实例的创建:
'''
树的构建:
3
9 20
15 7
'''
class Tree():
'树的构造'
def __init__(self,data, left = 0, right = 0):
self.data = data
self.left = left
self.right = right
def __str__(self):
return str(self.data)
class MyTree():
'二叉树的实现'
def __init__(self,base = 0):
self.base = base
def _Empty(self):
'判断是否为空树'
if self.base == 0:
return True
else:
return False
def front_search(self,tree_base):
'前序遍历:根-左-右'
if tree_base == 0:
return
print(tree_base.data)
self.front_search(tree_base.left)
self.front_search(tree_base.right)
def middle_search(self,tree_base):
'中序遍历:左-根-右'
if tree_base == 0:
return
self.middle_search(tree_base.left)
print(tree_base.data)
self.middle_search(tree_base.right)
def behind_search(self,tree_base):
'后序遍历:左-右-根'
if tree_base == 0:
return
self.behind_search(tree_base.left)
self.behind_search(tree_base.right)
print(tree_base.data)
# test tree
tree1 = Tree(data=15)
tree2 = Tree(data=7)
tree3 = Tree(20,tree1,tree2)
tree4 = Tree(data=9)
base = Tree(3,tree4,tree3)
btree = MyTree(base)
print('前序遍历:')
btree.front_search(btree.base)
print('中序遍历:')
btree.middle_search(btree.base)
print('后序遍历:')
btree.behind_search(btree.base)14.二叉搜索树:
又称为二叉排序树(二叉查找树),它或许是一棵空树,或许是具有以下性质的二叉树:
1.若它的左子树不为空,则左子树上所有的节点的值小于根节点的值
2.若它的右子树不为空,则右子树上所有的节点的值都大于根节点的值
3.它的左右子树也分别是二叉搜索树
###中序遍历可以按顺序排列
15.排序:
sorted(iterable, cmp=None, key=None, reverse=False)
lambda函数:
add = lambda x, y : x+y
add(1,2) # 结果为3
16.
快速排序:
def quick_sort(list1, start, end):
if start>=end:
return
left=start
right=end
mid=list1[left]
while leftlist1[left]:
left+=1
list1[left],list1[right]=list1[right],list1[left]
mid=list1[left]
quick_sort(list1,left+1,end)
quick_sort(list1,start,left-1) 归并排序:
def merge_sort(lst):
if(len(lst) <= 1):
return lst
left = merge_sort(lst[:len(lst)//2])
right = merge_sort(lst[len(lst)//2:len(lst)])
result = []
while len(left) > 0 and len(right)> 0:
if( left[0] > right[0]):
result.append(right.pop(0))
else:
result.append(left.pop(0))
if(len(left)>0):
result.extend(merge_sort(left))
else:
result.extend(merge_sort(right))
return result17.itertools.permutations(ss)
输出字符串排序的不同方法,每个方法一个组合,集合成一个非常规对象,有重复的
import itertools
class Solution:
def Permutation(self, ss):
# write code here
if not ss:
return []
return sorted(list(set(map(''.join, itertools.permutations(ss)))))
#map(''.join,A) 转化为字符串组成的对象
#set() 返回无重复元素集,降重;可以看作不能重复的集合,也可看做set()对象。
#list() 转化为列表
#sorted() 排序18.max( )函数、min( )函数:
max(x,y,z):返回x,y,z中最大元素。
max([1,1,2]):返回[1,1,2]中最大元素。(列表)
19.次数问题:创建字典,以元素为键,次数为值。
d={}
numbers=[1,1,2,2,2,3,3,3]
for i in numbers:
try:
dict[i]+=1
except:
dict[i]=1pop( )、get()、del
对字典排序用sorted排序:(列表既可用sort也可用sorted)
a={1:2,3:4,5:1}
b=dict(sorted(a.items(),key=lambda b:b[1]))
print(b)
20.考试执行时,多用try-except语句避免异常:
try-except
try:
fun()
do something1
expect:
do something2while-True-try-except(解决处理多个case)(最后再加,避免无法调试)
while True:
try:
a=sys.stdin.readline().strip()
if not a:
break
fun()
except:
break21.sorted( )和sort( )的小区别:
#sort()改变了a,且不能赋值给b。
a=[1,4,3,2]
a.sort()
print(a)
#sorted()未改变a,改变后的对象赋值给b。
a=[1,4,3,2]
b=sorted(a)
print(a,b)22.tab与空格的问题:
(1)tab与空格不能混用:同一列不能一个用tab,一个用空格。(pycharm里处理过的,所以只要对齐,就不用担心)
(2)建议缩进都用4个空格的长度(考试时一定要检查)
23.python中,{集合}不支持索引。
24.题义有时候很迷,直接看输入描述、输出描述,看的还明白些。
25.tuple可以作为字典的键,list不能。
26.字符串函数find、rfind
s.find('a'):返回s中a的最小索引
s.rfind('a'):返回s中a的最大索引
列表函数index
list.index(a):返回list中a的最小索引
27.collections库
import collections
d = collections.OrderedDict() #有序字典(输出顺序与添加顺序有关//无序字典无关)
a = collections.Counter(b) #计数器,Counter类型,加dict变成计数字典28.if和elif的区别:
if:会一直遍历完所有的if,不管你想判断的条件有没有遍历到,他都会继续执行完所有的if。
elif :走到符合查询条件的语句后,后面所有的elif和else就不会再被执行。
29.五大算法思想(最优解算法):
(1)贪心算法:
在对问题求解时,总是作出在当前看来是最好的选择。(一件事情分为很多步,每步都做最好的选择)(局部最优>>全局最优,必须无后效性)
(2)动态规划算法:
每次决策依赖于当前状态,又随即引起 ‘状态的转移’。一个‘决策序列’就是在变化的状态中产生出来的,所以,这种多阶段最优化决策解决问题的过程就称为动态规划。(经分解后得到的子问题往往不是互相独立的,即下一个子阶段的求解是建立在上一个子阶段的解的基础上,进行进一步的求解)
(3)分治法:
分治法的设计思想是:将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
(4)DFS(深度优先搜索、回溯法):
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。
(5)BFS(广度优先搜索、分支限界法):
类似于回溯法,也是一种在问题的解空间树T上搜索问题解的算法。但在一般情况下,分支限界法与回溯法的求解目标不同。回溯法的求解目标是找出T中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解,即在某种意义下的最优解。
30.图:
32.哈希表(散列表):
哈希表(Hash table,也叫散列表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表或哈希表。具体表现为: 存储位置 = f(key)
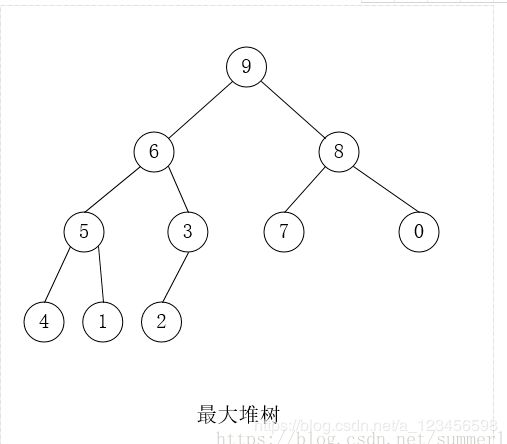
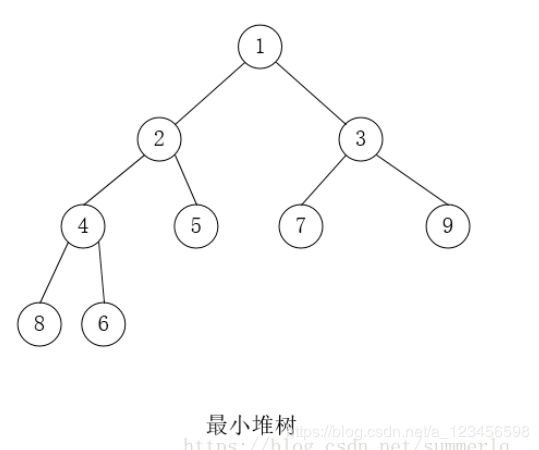
33.堆:
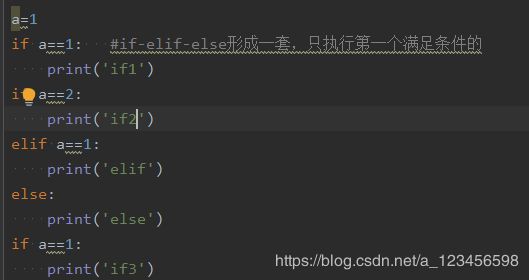
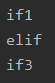
34.if-elif-else形成一套,只执行第一个满足条件的;后面再遇到if就是第二套:
输出:
35.round(x,2) #把x换为两位小数的浮点型
36.平衡二叉树(AVL):
定义:
一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
平衡树的判定:
#遍历每个结点,借助一个获取树深度的递归函数,根据该结点的左右子树高度差判断是否平衡,然后递归地对左右子树进行判断。
class Solution:
def IsBalanced_Solution(self, pRoot):
# write code here
if pRoot == None:
return True
if abs(self.TreeDepth(pRoot.left)-self.TreeDepth(pRoot.right)) > 1:
return False
return self.IsBalanced_Solution(pRoot.left) and self.IsBalanced_Solution(pRoot.right)
def TreeDepth(self, pRoot): #计算树的深度
# write code here
if pRoot == None:
return 0
nLeft = self.TreeDepth(pRoot.left) #左子树的深度
nRight = self.TreeDepth(pRoot.right)
return max(nLeft+1,nRight+1)37.return可以返回一个判定语句,根据语句真实性选择True或False。
38.字符串:
(1)join() 方法用于将序列中的元素以指定的字符连接生成一个新的字符串
str.join(sequence)