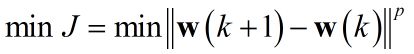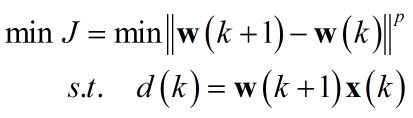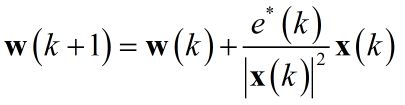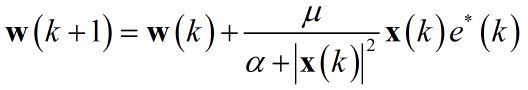自适应滤波：LMS/NLMS
转自：http://www.cnblogs.com/xingshansi/p/6658203.html
前言
西蒙.赫金的《自适应滤波器原理》第四版第五、六章：最小均方自适应滤波器（LMS，Least Mean Square）以及归一化最小均方自适应滤波器（NLMS，Normalized Least Mean Square）。全文包括：
1）LMS与维纳滤波器（Wiener Filter）的区别；
2）LMS原理及推导；
3）NLMS推导；
4）应用实例；
内容为自己的读书记录，其中错误之处，还请各位帮忙指出！
一、LMS与维纳滤波器（Wiener Filter）的区别
- 这里介绍的LMS/NLMS，通常逐点处理，对应思路是：随机梯度下降；
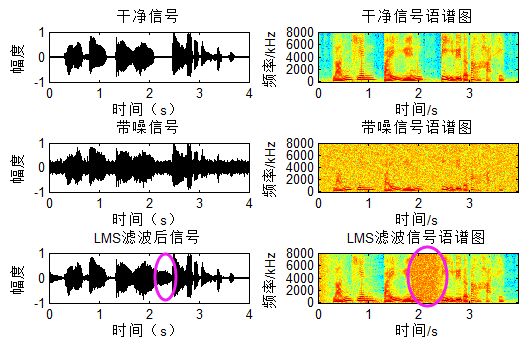
- 对于Wiener Filter，给定准则函数J，随机/批量梯度都可以得出最优解；
- LMS虽然基于梯度下降，但准则仅仅是统计意义且通常引入误差，可以定义为
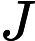
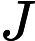J0，简而言之 J通常不等于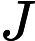 J0，得出的最优解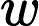 
wo自然也通常不等于维纳最优解； - 分析LMS通常会分析稳定性，稳定性是基于Wiener解，之前已给出分析。但LMS是Wiener解的近似，所以：迭代步长的稳定性，严格适用于Wiener解，对于LMS只是一种近似参考，并没有充分的理论依据。
下文的分析仍然随机梯度下降的思路进行。
二、LMS原理及推导
LMS是时间换空间的应用，如果迭代步长过大，仍然有不收敛的问题；如果迭代步长过小，对于不平稳信号，还没有实现寻优就又引入了新的误差，屋漏偏逢连夜雨！所以LMS系统是脆弱的，信号尽量平稳、哪怕短时平稳也凑合呢。
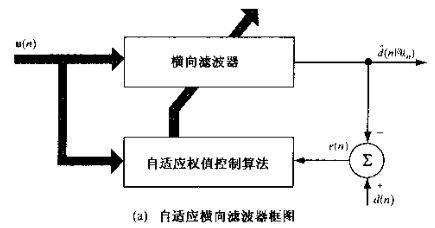
给出框图：
关于随机梯度下降，可以参考之前的文章。这里直接给出定义式：
利用梯度下降：
−∇J=x(wTx−d)T
给出LMS算法步骤：
1）给定
w(0)，且
1<μ<1/λmax；
2）计算输出值：
y(k)=w(k)Tx(k);
3）计算估计误差：
4）权重更新：
三、NLMS推导
看到Normalized，与之联系的通常是约束条件，看到约束不免想起拉格朗日乘子。思路有了，现在开始分析：
假设 
w(k)⇒w(k+1)得到最优权重，即：
d(k)=w(k+1)x(k)
我们希望在得到期望权重的附近，迭代不要过大以免错过最优值：
写出准则函数：
利用之前文章提到的拉格朗日乘子法：
这里仅仅分析基于欧式距离 
p=2的情形，其它范数类似。求解得出:
通常为了防止分母为零迭代方程需要修正，而修正后步长存在偏差，故添加调节因子 
μ：
给出NLMS算法步骤：
1）给定
2）计算输出值：
3）计算估计误差：
4）权重更新：
四、应用实例
A-自适应噪声滤波
这个场景可以简化为：一个房间两个麦克风，一个放在远处采集房间噪声，一个放在说话人附近采集带噪语音，认为两个音频文件的噪声相似。
这里噪声直接用白噪声，对应实际场景可以认为是采集的噪声数据，给出主要代码：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
[s, fs, bits] =
wavread
(filename);
s=s-
mean
(s);
s=s/
max
(
abs
(s));
N=
length
(s);
time=(0:N-1)/fs;
%%生成带噪信号
clean=s';
ref_noise=0.1*
randn
(1,
length
(s));
mixed = clean+ref_noise
%NLMS
mu=0.05;M=32;espon=1e-4;
% [en,wn,yn]=lmsFunc(mu,M,ref_noise,mixed);%
[en,wn,yn]=nlmsFunc(mu,M,ref_noise,mixed,espon);
|
LMS代码：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
function
[e,w,ee]=lmsFunc(mu,M,u,d)
% Normalized LMS
% Call:
% [e,w]=nlms(mu,M,u,d,a);
%
% Input arguments:
% mu = step size, dim 1x1
% M = filter length, dim 1x1
% u = input signal, dim Nx1
% d = desired signal, dim Nx1
% a = constant, dim 1x1
%
% Output arguments:
% e = estimation error, dim Nx1
% w = final filter coefficients, dim Mx1
%intial value 0
w=
zeros
(M,1);
%This is a vertical column
%input signal length
N=
length
(u);
%make sure that u and d are colon vectors
u=u(:);
d=d(:);
%NLMS
ee=
zeros
(1,N);
for
n=M:N
%Start at M (Filter Length) and Loop to N (Length of Sample)
uvec=u(n:-1:n-M+1);
%Array, start at n, decrement to n-m+1
e(n)=d(n)-w'*uvec;
w=w+2*mu*uvec*e(n);
% y(n) = w'*uvec; %In ALE, this will be the narrowband noise.
end
|
NLMS代码：
对应结果图：
可以看出LMS/NLMS在最开始都有一个自适应的过程。
NLMS基于信号 
x的能量实现变步长，信号大步长小，信号小则步长大：目标信号明显，则迭代细致，不明显，则一带而过，呵呵，跟平时看书还挺像，聪明的孩子。
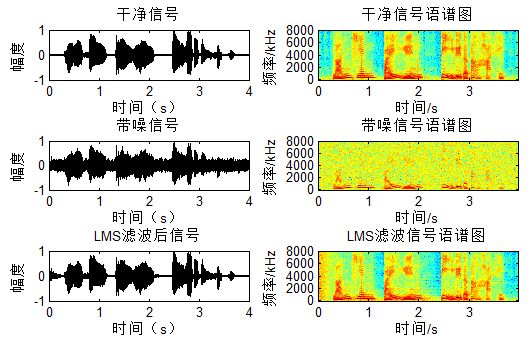
再来看一组信号：
这里在中间令噪声突变，可以看到滤波器又需要重新自适应，因此对于短时平稳LMS勉强使用，如果不断变呢？非平稳LMS自然无效了，这个时候就需要Kalman Filter来搭把手。
B-工频噪声滤波
现在有一个音频信号，分析频谱：
可以看到信号带有明显的 
50Hz噪声，我们知道 50Hz的正弦与余弦可以组合成任意相位的 50Hz频率信号，基于这个思路，进行自适应滤波：
给出主要的代码：
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
x1=
cos
(2*
pi
*50*time);
x2=
sin
(2*
pi
*50*time);
w1=0.1;
w2=0.1;
e=
zeros
(1, N);
y=
zeros
(1, N);
mu=0.05;
for
i
=1: N
y(
i
)=w1 * x1(
i
)+ w2 * x2(
i
);
e(
i
) =x(
i
)-y(
i
);
w1=w1+mu * e(
i
) * x1(
i
);
w2=w2+mu * e(
i
) * x2(
i
);
end
|
结果图可以看出，工频50Hz滤除：
基于LMS的应用还有很多，不一一说啦。
参考：
- Simon Haykin 《Adaptive Filter Theory Fourth Edition》.
- 宋知用：《MATLAB在语音信号分析和合成中的应用》.