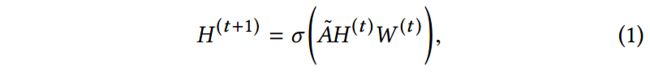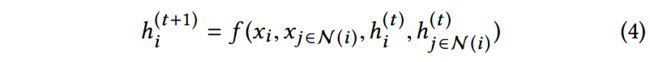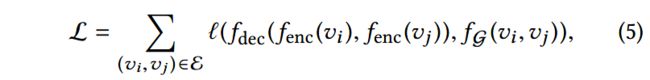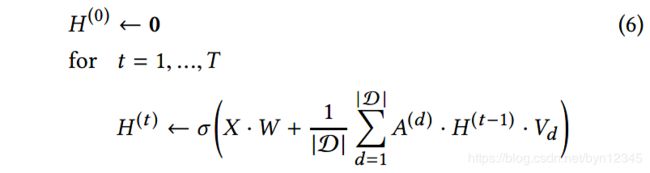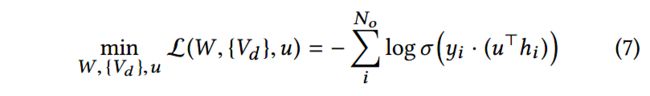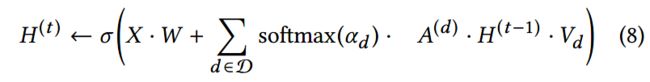【论文解读 CIKM 2018 | GEM】Heterogeneous Graph Neural Networks for Malicious Account Detection
论文链接:https://arxiv.org/abs/2002.12307
来源:CIKM 2018
官方介绍:https://zhuanlan.zhihu.com/p/48243724
文章目录
- 1 摘要
- 2 介绍
- 3 预备知识
- 3.1 GNN
- 3.2 Node Embedding
- 4 提出的方法
- 4.1 数据分析
- 4.1.1 设备聚集
- 4.1.2 行为聚集
- 4.2 A Motivation: Subgraph Components
- 4.3 Heterogeneous Graph Construction
- 4.4 模型
- 4.5 注意力机制
- 5 实验
- 6 总结
1 摘要
本文提出GEM模型,是一个异质图神经网络方法,用于在支付宝中检测恶意账户。
本文的方法受连通子图方法的启发,基于攻击者的两个基本弱点,从异质的账户-设备(account-device)图中自适应地学习到embedding。
使用了自注意力机制,为不同类型的节点分配不同的注意力。聚合每种节点的信息时,使用的是求和(sum)的方式。
2 介绍
要能检测出恶意账户,首先要研究恶意账户的攻击特征。现有的研究主要从三个方面展开:
(1)基于规则的方法:使用复杂的规则,识别恶意账户。
(2)基于图的方法:考虑用户之间的关联,恶意账户和异常账户之间有关联。
(3)基于机器学习的方法:利用大量的历史数据,建立统计模型。
攻击策略是会不断变化的,所以需要有一个能适应不断变化的策略的检测系统。
作者总结了来自攻击者的两个主要特征:
(1)设备聚集(Device aggregation)
攻击者要承受计算资源带来的成本,所以大多数攻击者只在少数计算资源上注册或频繁地登录。
(2)行为聚集(Activity aggregation)
攻击者受攻击时间的限制,通常要在很短的时间内完成既定目标,所以恶意账户的行为可能在有限的时间内爆发。
虽然我们已经广泛分析了攻击者的弱点,但保证识别的高准确率和高召回率还是非常有挑战性的。
现有的方法通常假阳率(FP, 模型判断是恶意账户,实际上不是)很低,也就是假阴率(FN, 模型判断不是恶意账户,实际上是)很高,这样虽然对用户友好,避免误伤,但是可能会错过识别出更多可疑账户的机会。这是因为,大量的良性账户和少量的可以账户交织在一起,形成了低信噪比。
因此,在不同设备构成的异构图中同时考虑"设备聚集"和"行为聚集"是很重要的。
本文提出GEM模型(Graph Embeddings for Malicious accounts),同时考虑了异质图中的“设备聚集”和“行为聚集”,是一种基于图网络的图表示学习方法。
本文提出的方法本质上是对异质的account-device图进行建模,同时考虑了局部结构中账户的行为特征。
模型的基本思想是:账户是正常的还是恶意的,取决于其他账户是如何通过设备与该账户聚集的,以及那些与该账户共享同一设备的账户的行为表现是什么样子的。
本文贡献如下:
(1)提出基于图表示方法的神经网络,同时关注攻击者“设备聚集”和“行为聚集”两个特点,以实现对恶意账户的检测。是第一个使用GNN方法进行欺诈检测的工作。
(2)本文的模型已在支付宝中应用,每天可以有效检测出上万的恶意账户。
3 预备知识
3.1 GNN
Kipf提出的GCN是在接地那的一阶邻居上进行卷积。 X ∈ R N , D X\in R^{N,D} X∈RN,D是节点特征向量 x i ∈ R D x_i\in R^D xi∈RD组成的矩阵。无向图 G = ( V , E ) G=(V,E) G=(V,E),有 N N N个节点 v i ∈ V v_i\in V vi∈V,边 ( v i , v j ) ∈ E (v_i,v_j)\in E (vi,vj)∈E,邻接矩阵为 A ∈ R N × N A\in R^{N\times N} A∈RN×N。卷积层计算如下:
其中 A ~ \tilde{A} A~是 A A A添加self-loops后对称归一化(symmetric normalization )的结果: A ~ = D ^ − 1 2 A ^ D ^ − 1 2 , A ^ = A + I \tilde{A}=\hat{D}^{-\frac{1}{2}}\hat{A}\hat{D}^{-\frac{1}{2}}, \hat{A}=A+I A~=D^−21A^D^−21,A^=A+I, D ^ \hat{D} D^是 A ^ \hat{A} A^中节点度的对角矩阵。
关于GCN的解释可以参考这位大佬的博客,总结的非常好:
图卷积网络 GCN Graph Convolutional Network(谱域GCN)的理解和详细推导-持续更新
GCN学习到了函数 f ( X , A ) f(X,A) f(X,A),使用 A A A中节点 v i v_i vi的邻居信息表示该节点。
文章中还介绍了两个GNN的工作
总之,GNN的工作可以看成是递归地聚合邻居信息的方法:
GNN中大多数的工作都是围绕"感受野(receptive fileds)"的研究,也就是进行聚合的范围。图结构的数据时非欧式的,每个节点的邻居数目不确定,不像图像数据每个像素点就只有8个邻居。
有学者提出了GeniePath,可以自适应地为每个节点设定不同的感受野,而不像GCN那样预先设定好卷积的感受野。
本文的工作可以看成是GCN的变形。作者使用求和(sum)的操作捕获每个节点 T T T步邻居聚合来的信息,并且使用注意力机制衡量不同类型节点的重要性。
3.2 Node Embedding
图嵌入学习的目的是,保留图结构的同时学习到节点的表示。
大多数方法目的都是最小化如下的衡量重构能力的经验损失:
4 提出的方法
4.1 数据分析
本节研究了支付宝中真实数据的“设备聚集”和“行为聚集”的特性。
4.1.1 设备聚集
基本思想是:若一个账户与大量的其他账户一起注册或邓丽同一组设备,则这些账户就会被怀疑是恶意账户。
计算连通子图的规模,衡量账户的风险。
4.1.2 行为聚集
基本思想是:如果共享设备的账户成批运行,则这些账户就是可疑的。使用向量内积作为衡量标准,例 S i , i ′ a = < x i , x i ′ > S^a_{i,i^{'}}=
这样的度量两个账户关联性的方法,可以用于对连通子图进行进一步分割,来提高假阳性概率。
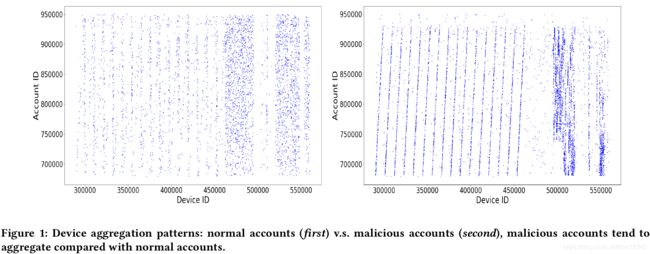
上图表示设备聚集,展示了支付宝中连续7天的account-device数据图。对于正常账户,蓝色的点均匀分布在图中。对于恶意账户,点的分布表明特定的设备以不同的模式连接了大量的账户。
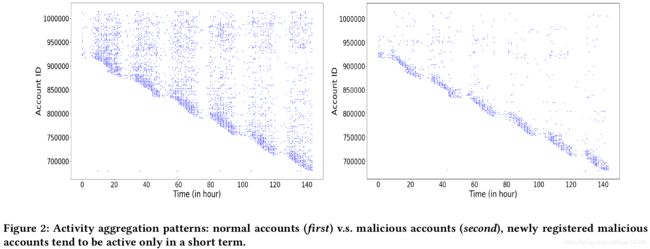
上图表示行为聚集,展示了账户在不同时间的行为模式。左图的正常账户的行为显示,每个新注册的账户在未来几天内的行为是均匀分布的。而右图中的恶意账户的行为往往只在短时间内爆发。
4.2 A Motivation: Subgraph Components
上述的设备和行为聚集模式启发了作者。
第一步尝试称为“连通子图(connected subgraph)”。
基本思想是建立账户构成的图,希望用边建立起一组账户。连通子图方法由以下三步组成:
(1)给定图 G = ( V , E ) G=(V,E) G=(V,E),有 N N N个节点, M M M条边。 { ( i , j ) } {\{(i,j)\}} {(i,j)}表示账户 i i i在设备 j j j上有登录行为。目标是构建一个由账户节点构成的同质图 G a = ( V a , E a ) G^a=(V^a,E^a) Ga=(Va,Ea),边 ( i , i ′ ) (i,i^{'}) (i,i′)表示账户 i i i和 i ′ i^{'} i′有一段时间在同一设备上登录。
这样,同质图 G a G^a Ga就由多个连通子图所构成,每个子图表示一组账户。这组账户数量越多,则为恶意账户的风险越大。
但是实际操作中有很多噪声,例如不同账户登录相同的ip地址,混淆正常账户和恶意账户的现象很普遍。
(2)接着按照如下的方法删除掉一些边。由图2所示,异常账户的行为通常在特定的一天内爆发。为了衡量 G a G^a Ga中两个账户节点间的相似性,使用向量 x i = [ x i , 1 , . . . , x i , p ] ⊤ x_i=[x_{i,1},...,x_{i,p}]^\top xi=[xi,1,...,xi,p]⊤表示账户 i i i的行为, x i , t x_{i,t} xi,t表示账户 i i i在第 t t t小时行为的频率。
使用内积运算 x i ⊤ x i ′ x^{\top}_i x_{i^{'}} xi⊤xi′衡量两个账户之间的相似度。若 x i ⊤ x i ′ < θ x^{\top}_i x_{i^{'}}<\theta xi⊤xi′<θ,则在图 G a G^a Ga中删除边 ( i , i ′ ) (i,i^{'}) (i,i′)。 θ \theta θ是一个调节 G a G^a Ga稀疏性的超参数。
(3)使用每个账户所属的子图的大小为其打分。
尽管该方法可以在最大的连通子图中准确检测出恶意账户,但是它不能很好地在较小的连通子图中检测出恶意账户。
能不能使用机器学习方法进行恶意账户识别呢?与传统的先提取特征 X X X然后学习判别函数 f ( X ) f(X) f(X)的方法不同,能否同时使用特征和图的结构,直接学习得到 f ( X , G ) f(X,G) f(X,G)呢?
从上述构建连通子图的3步可以观察到两点:
(1)连通子图的评分由以下两点确定:1)每个点和邻居的连通性;2)一个连通子图中的节点数目,
连通性取决于 G a G^a Ga(设备聚集)的结构以及节点间的向量内积(行为聚集)。子图中节点的数目反映了连通性的强度。
(2)还需要一个将account-device图 G G G转换为account-account图 G a G^a Ga的转换函数。
4.3 Heterogeneous Graph Construction
假定 N N N个节点包括账户和设备,每个设备都对应一个类型 d ∈ D d\in D d∈D。给出在时间范围 [ 0 , T ) [0,T) [0,T)的 M M M条账户和设备之间的连边 { ( i , j ) } {\{(i,j)\}} {(i,j)}。每条边都表示账户 i i i在设备 j j j上有行为,例如注册、登录等。对于包含 N N N个节点的图 G = ( V , E ) G=(V,E) G=(V,E),有邻接矩阵 A ∈ { 0 , 1 } N , N A\in{\{0,1\}}^{N,N} A∈{0,1}N,N。
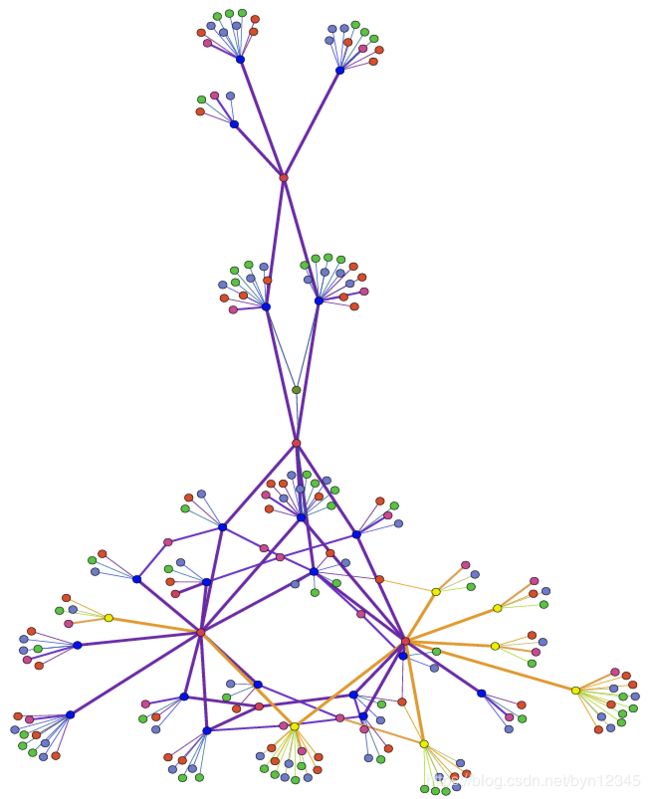
图 G G G中的一个连通子图展示如下,其中蓝色节点是正常账户,黄色节点是异常账户:
为了方便,作者按照设备(device)的类型,抽取出了 ∣ D ∣ |D| ∣D∣个子图 { G ( d ) = ( V , E ( d ) ) } {\{G^{(d)}=(V,E^{(d)})\}} {G(d)=(V,E(d))},每个子图都包含了 G G G中的所有节点。
注意,这里设备的概念比较宽泛,例如设备可以是IP地址、电话号码、User Machine ID(UMID)、MAC地址、IMSI(International Mobile Subscriber Identity)、APDID(Alipay Device ID)、TID,这就构成了异质图。
在这些图的基础上,进一步处理每个账户的行为。假定矩阵 X ∈ R N , p + ∣ D ∣ X\in R^{N,p+|D|} X∈RN,p+∣D∣,若 i i i是账户节点则每一行 x i x_i xi表示了节点 i i i的行为。
账户 i i i在时间范围 [ 0 , T ) [0,T) [0,T)内的行为可以分为 p p p个时间小段,每一个时间小段表示账户在这段时间产生行为的次数。
对于和该账户相关联的设备,只需使用将向量的最后 ∣ D ∣ |D| ∣D∣维根据所属设备,编码成one-hot向量就可以了。
最终的目的是:
给定邻接矩阵 A A A、在 [ 0 , T ) [0,T) [0,T)时间内的行为矩阵 X X X,以及在 [ 0 , T − 1 ) [0,T-1) [0,T−1)时间内 N 0 N_0 N0个已标注账户是否为恶意账户的标签,学习到函数 f ( { A d } , X ) f({\{A^d\}},X) f({Ad},X),正确预测在 T T T时刻的恶意账户。
4.4 模型
上述章节讨论了数据中发现的模式(“设备聚集”和“行为聚集”),以及异质图的构建。并且说明了这些模式可以通过给定 A , X A, X A,X的函数学习得到。
仍然需要一个强大的函数来捕获这些模式。
我们希望通过聚合转换后的行为矩阵 X X X,从而为每个节点 i i i学习到有效的embedding h i h_i hi:
其中, H ( t ) ∈ R N , k H^{(t)}\in R^{N,k} H(t)∈RN,k表示 t t t层的嵌入矩阵,每行表示一个节点的embedding。 T T T表示节点跳数,也表示隐藏层的层数。 W , { V d } W, {\{V_d\}} W,{Vd}是需要优化的参数。
随着迭代的加深(例如T步),节点就可以在隐层聚合T-step的邻居信息,这就和连通子图中定义的打分函数(计算连通子图中的节点数)有相似之处。区别在于,我们的方法是在原始的account-device图上工作的,通过将T-step邻居的行为嵌入求和,来讲节点映射到隐层空间。
损失函数定义如下:
使用EM算法优化,在e-step,基于参数 W W W和 { V d } {\{V_d\}} {Vd}使用(6)式计算embeddings;在m-step,优化(7)式中的参数并调整embeddings。
本文的方法可以看成是GCN的变形,主要区别在于:
1)本文的算法可以用于HIN;
2)聚合函数是不同的,本文的模型对不同类型的图 G ( d ) G^{(d)} G(d)中的两种模式(设备聚集和行为聚集)进行的是求和操作,然后按照图类型的数目取了均值。
4.5 注意力机制
引入注意力机制,在学习过程中自适应地为不同类型的子图分配注意力:
5 实验
数据集:Alipay(支付宝)
实验任务:
对比方法:
- 连通子图:4.2中提出的方法
- GBDT+Graph:一种基于机器学习的方法,GBDT全称为Gradient Boosting Decision Tree
- GBDT+Node2Vec:基于随机游走的节点嵌入方法
- GCN:经典的图卷积网络方法,聚合公式是(1)式
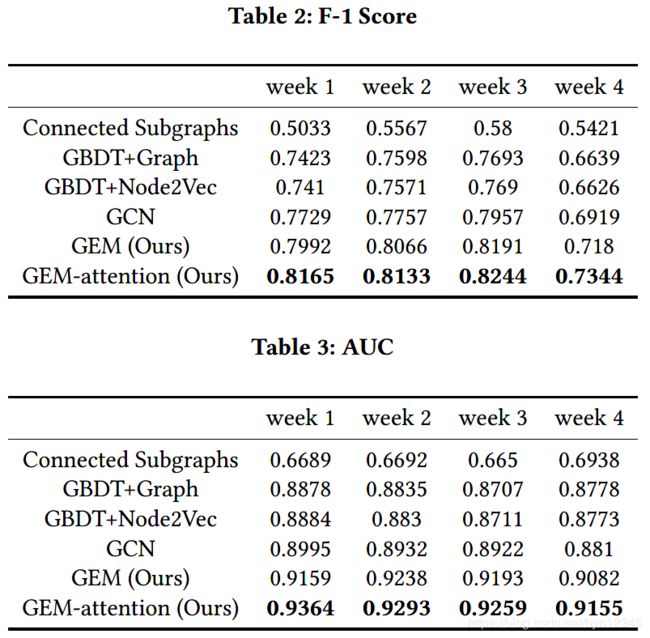
实验结果:
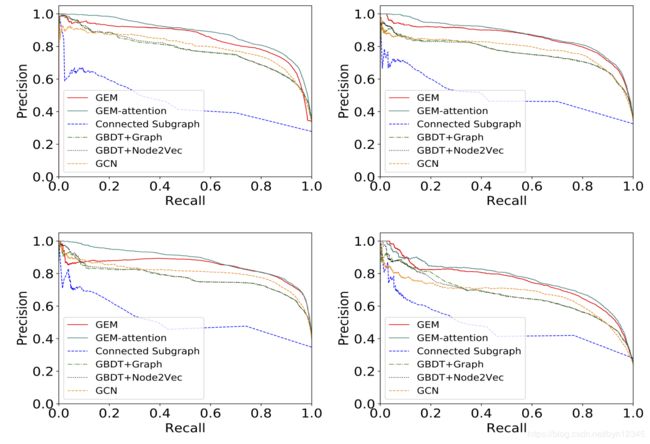
不同方法在测试集上,第1,2,3,4周的precision-recall曲线对比如下:
6 总结
本文提出了GEM模型,用于日常在支付宝中恶意账户的发现。
总结了攻击者的两个基本特点:设备聚集、行为聚集。
是第一个使用GNN方法实现欺诈检测的方法。
未来的工作:在随时间变化的动态图上建立恶意账户检测系统。
正如作者所说,这个应用场景实际上应该是应用动态图的,这也是未来的一个研究方向。动态图很难做。