25 近似推断 Approximate Inference

这一讲，主要是从一些宏观的角度来描述了一下近似推断的方法和思想。几乎所有的无向图都会涉及到推断(Inference) 的问题。概率图模型的三大问题分别是，表示(Representation)，学习(Learning)和推断问题(Inference)。本节侧重从深度学习的角度来看一下Inference。

1 Background

1.1 推断的目的

首先我们要明确推断的目的是什么？我们为什么要进行推断，我们假设$v$ 是可观测变量，$h$ 是不可观测的隐藏变量。推断的目的可以分为以下两个部分。

1.1.1 推断本身的意义

推断行为，求解的是在给定观测变量下，隐藏变量的后验概率分布，即为$P(h|v)$。这是一种对原因的追溯，就像当我们看到一个事实的时候，去想他为什么会发生，这本身就很有意义。

1.1.2 Learning 问题中的运用

在Learning 的过程中，很多时候我们都用到了推断。比如在EM 算法中，第一步是求关于$P(h|v)$的后验下，关于$P(h,v)$ 的期望，然后在令这个函数最大化。这是一个反复迭代的过程，在最大化的过程中，我们要知道$E_{P(h|v,\theta (t))}[P(h,v,\theta )]$ 的参数化表达形式，所以避免不了求$P(h|v,\theta (t)0$ 的过程。所以在学习的过程中，经常涉及到Inference 的问题。

1.2 为什么要近似推断？

为什么要近似近似推断呢？因为大部分情况下，精确推断实在是太复杂了，基本上是intractable。为了解决这个大问题，诞生了很多近似推断的方法，为什么会造成这个原因呢？我们看看下面四个模型，为了方便描述，假设每个节点都是离散随机变量，服从伯努利分布(0/1 分布)。

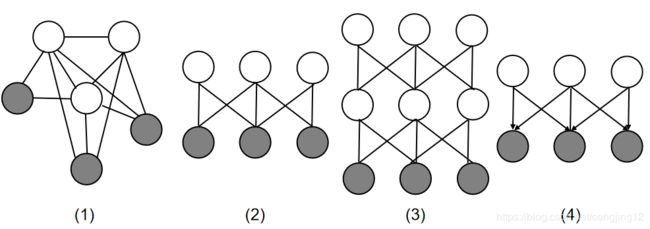
图1: Boltzmann Machine，Restricted Boltzmann Machine，Deep Boltzmann Machine 和Sigmoid Belief Network 的概率图模型，灰色的节点代表$v$，白色的节点代表$h$。

1.2.1 Boltzmann Machine

图一中的(1) 就是Boltzmann Machine，它的理论依据是很好的，但是并没有很好的办法去解决它。无向图求解概率密度分布，需要转换成最大团势函数的乘积，而Boltzmann Machine 中节点之间的关系过于复杂，很难被分解。所以导致计算基本是intractable 的。无向图的后验不好处理的原因就是连接本身带来相互作用，不容易进行分解，这是无向图模型的硬伤。

1.2.1 Boltzmann Machine

图一中的(1) 就是Boltzmann Machine，它的理论依据是很好的，但是并没有很好的办法去解决它。无向图求解概率密度分布，需要转换成最大团势函数的乘积，而Boltzmann Machine 中节点之间的关系过于复杂，很难被分解。所以导致计算基本是intractable 的。无向图的后验不好处理的原因就是连接本身带来相互作用，不容易进行分解，这是无向图模型的硬伤。

1.2.2 Restricted Boltzmann Machine

图一中的(2) 就是Restricted Boltzmann Machine，在这个概率图模型中，可以看到，h 和v 集
合内部的节点都是互相独立的，而集合之间的节点都是相互连接的。结点内部的节点相互独立性可以通过局部马尔可夫性质证明。

1.2.3 Deep Boltzmann Machine

图一中的(3) 就是Deep Boltzmann Machine，很显然虽然第三层是可观测的，而第一层和第二层节点之间的关系函数很复杂，不可做到相互独立，相互分离，那么同样还是intractable，无法处理。只有当两层是可观测的之后，剩下的那层节点之间才是相互独立的。

1.2.4 Sigmoid Belief Network

图一中的(4) 就是Sigmoid Belief Network，网络中的概率图模型是有向的，同样P(h|v) 是求不
出来的。根据D-Separation 中Head to Head 的结构。当中间节点被观测到时，两个head 节点是有关系的，不是相互独立的。那么，h 节点之间就是无法分解的，后验分布求解依然很困难，这就是有向图的explain away 问题。
如果，条件分布是Gaussian Distribution 就很优美了，根据Gaussian 分布的自共轭性，他的条件，联合概率分布都是Gaussian 的，这就很好办了，我们之前有用待定系数的方法俩求这个后验概率分布。

1.2.5 小结

关于无向图精确推断主要问题就是节点之间的mutual interaction；有向图精确推断主要问题就是explain away。

2 推断即优化

2.1 变分推断

由于精确推断的难度很高，所以近似推断崛起了。比如EM 系列和VI 系列。
可以将可观测变量的Log Likelihood 转为一个优化ELBO 下界和KL 散度的形式，从而优化
ELBO 下界就可以了。Log Likelihood 公式表达如下所示：
$$\frac{1}{N}\sum _{v}logP(v)$$

而$logP(v)$，可以表达为：
$$\log p(v)=\log \frac{p(h,v)}{p(h|v)}=\log p(h,v)-\log p(h|v)=\log \frac{p(h,v)}{q(h|v)}-\log \frac{p(h|v)}{q(h|v)}$$
将等式两边都乘上 $q(h|v),$ 可以得到：
$$q(h|v)\log p(v)=q(h|v)\left(\log \frac{p(h,v)}{q(h|v)}-\log \frac{p(h|v)}{q(h|v)}\right)$$
因为 $q(h|v)$ 是一个关于 $h$ 的函数，我们将等式两边对 $p(v)$ 和 $h$ 没有关系，而$\int q(h|v)=1,$所以有
$$\int q(h|v)\log p(v)dh=\log p(v)\int q(h|v)dh=\log p(v)$$
那么有,
$$\begin{array}{rl}\log p(v)& =\int q(h|v)\left[\log \frac{p(h,v)}{q(h|v)}-\log \frac{p(h|v)}{q(h|v)}\right]dh\\ & =\int q(h|v)\left[\log \frac{p(h,v)}{q(h|v)}\right]dh-\int q(h|v)\left[\log \frac{p(h|v)}{q(h|v)}\right]dh\\ & =\int q(h|v)\left[\log \frac{p(h,v)}{q(h|v)}\right]dh+\int q(h|v)\left[\log \frac{q(h|v)}{p(h|v)}\right]dh\\ & =\underset{\mathrm{E}\mathrm{L}\mathrm{B}\mathrm{O}}{{\mathbb{E}}_{q(h|v)}\left[\log \frac{p(h,v)}{q(h|v)}\right]}+\mathrm{K}\mathrm{L}[q(h|v)\Vert p(h|v)]\\ & \le {\mathbb{E}}_{q(h|v)}\left[\log \frac{p(h,v)}{q(h|v)}\right]\end{array}$$
因为KL 散度是很大于0 的，那么我们只要优化ELBO 就可以优化$p(v)$ 了，这就是优化下界的方法。
而ELBO 可以继续化简为：
$$\begin{array}{rl}{\mathbb{E}}_{q(h|v)}\left[\log \frac{p(h,v)}{q(h|v)}\right]& ={\mathbb{E}}_{q(h|v)}[\log p(h,v)-\log q(h|v)]\\ & ={\mathbb{E}}_{q(h|v)}[\log p(h,v)]-{\mathbb{E}}_{q(h|v)}[\log q(h|v)]\\ & ={\mathbb{E}}_{q(h|v)}[\log p(h,v)]+\mathrm{H}(q(h|v))\end{array}$$

我们可以将ELBO 函数看成$\mathcal{L}(v,h,q)(q(h|v)$ 是一个函数，函数的函数被称为泛函)。我们的目标就是优化这个函数，从而达到计算$P(v)$。$p(v)$ 是一个未知的客观真理，所以我们把它当成一个常量来看，而最大化ELBO，实际上也在最小化KL 散度。所以，这个算法的目的就是找一个简单的q(h|v) 去靠近$p(h|v)$，这个$p(h|v)$ 是不是就是推断。所以说，推断即优化。

2.2 小结

本小节主要是通过变分推断的例子来揭示了为什么说推断就是优化，在变分推断的例子中，我用最大化ELBO 来使一个简单的分布$q(h|v)$ 来逼近$p(h|v)$。

3 总结

本章，首先介绍了推断的目的是什么，1. 寻找事情发生的原因；2. Learning 问题中的使用。然后，分无向图和有向图介绍了精确推断的难点，无向图精确推断主要问题就是节点之间的mutual interaction；有向图精确推断主要问题就是explain away。从而引出了近似推断，然后用变分推断的例子来讲述了推断即优化的思想。整个过程比较流畅。