VAE 变分自动编码器入门

概率论复习

熟悉的旁友直接跳过这一章节吧

贝叶斯公式

$$P(A|B)=\frac{P(A)\times P(B|A)}{P(B)}$$

其中P(A|B)是指在事件B发生的情况下事件A发生的概率。

在贝叶斯定理中，每个名词都有约定俗成的名称：

• $P(A|B)$是已知$B$发生后$A$的条件概率，也由于得自$B$的取值而被称作$A$的后验概率。
• $P(A)$是$A$的先验概率（或边缘概率）。之所以称为"先验"是因为它不考虑任何$B$方面的因素。
• $P(B|A)$是已知$A$发生后$B$的条件概率，也由于得自$A$的取值而被称作$B$的后验概率。
• $P(B)$是$B$的先验概率或边缘概率。

按这些术语，贝叶斯定理可表述为：

$$后验概率=(似然性\ast 先验概率)/标准化常量$$

也就是说，后验概率与先验概率和相似度的乘积成正比。

另外，比例P(B|A)/P(B)也有时被称作标准似然度（standardised likelihood），贝叶斯定理可表述为：

$$后验概率=标准似然度\ast 先验概率$$

全概率公式

$$P(A)=\sum _{n}P(A|B_n)P\left(B_n\right)$$

简单的理解就是，消去$B$事件对$A$事件的影响

最大似然估计

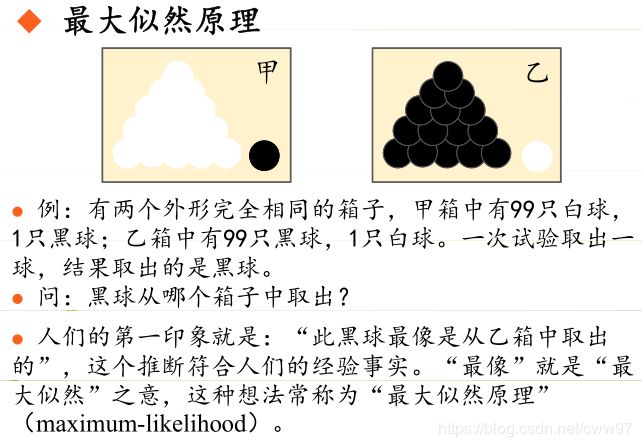
总结起来，最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

由于样本集中的样本都是独立同分布，可以只考虑一类样本集$D$，来估计参数向量$\theta$。记已知的样本集为：

$$D=\left\{x_1,x_2,\cdots ,x_N\right\}$$

似然函数（linkehood function）：联合概率密度$p(D|\theta )$函数称为相对于$\left\{x_1,x_2,\cdots ,x_N\right\}$的$\theta$的似然函数。

$$l(\theta )=p(D|\theta )=p\left(x_1,x_2,\cdots ,x_N|\theta \right)=\prod _{i=1}^{N}p\left(x_i|\theta \right)$$

如果$\hat{\theta }$是参数空间中能使似然函数$l(\theta )$最大的θ值，则$\hat{\theta }$应该是“最可能”的参数值，那么$\hat{\theta }$就是$\theta$的极大似然估计量。它是样本集的函数，记作：

$$\hat{\theta }=d\left(x_1,x_2,\cdots ,x_N\right)=d(D)$$

极大似然函数:ML估计：求使得出现该组样本的概率最大的θ值：

$$\hat{\theta }=\arg \underset{\theta }{\max }l(\theta )=\arg \underset{\theta }{\max }\prod _{i=1}^{N}p\left(x_i|\theta \right)$$

因为这是个连乘不太好求导，所以经常取个对数

$$H(\theta )=\ln l(\theta )$$

$$\hat{\theta }=\arg \underset{\theta }{\max }H(\theta )=\arg \underset{\theta }{\max }\ln l(\theta )=\arg \underset{\theta }{\max }\sum _{i=1}^N\ln p\left(x_i|\theta \right)$$

这个时候就到了大家熟悉的概率论书后习题了，全是加法，对$\theta$求导，解出导数为0的时候的

$$\frac{dH(\theta )}{d\theta }=\frac{d\ln l(\theta )}{d\theta }=0$$

如果$\theta$不止一个参数，那就求梯度吧，再议再议，有这么一个概念，下面的东西读起来可能不会出人命

KL散度

相对熵（relative entropy）又称为KL散度（Kullback–Leibler divergence，简称KLD），信息散度（information divergence），信息增益（information gain）。

KL散度是两个概率分布P和Q差别的非对称性的度量。 KL散度是用来 度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下，P表示数据的真实分布，Q表示数据的理论分布，模型分布，或P的近似分布。

对于离散随机变量，其概率分布P 和 Q的KL散度可按下式定义为

$$D_{\mathrm{K}\mathrm{L}}(P\Vert Q)=-\sum _{i}P(i)\ln \frac{Q(i)}{P(i)}$$

等价于

$$D_{\mathrm{K}\mathrm{L}}(P\Vert Q)=\sum _{i}P(i)\ln \frac{P(i)}{Q(i)}$$

即按概率P求得的$P$和$Q$的对数商的平均值。KL散度仅当概率$P$和$Q$各自总和均为$1$，且对于任何$i$皆满足 $Q(i)>0$及 $P(i)>0$时，才有定义。式中出现 $0\ln 0$的情况，其值按$0$处理。

对于连续随机变量，其概率分布P和Q可按积分方式定义为

$$D_{\mathrm{K}\mathrm{L}}(P\Vert Q)={\int }_{-\infty }^{\infty }p(x)\ln \frac{p(x)}{q(x)}\mathrm{d}x$$

emmm,这一段，似乎把公式记住就够用了

自动编码器

自动编码器是是个什么玩意呢

众所周知，图片一般，按像素存的话，very large，处理起起来极其的烧显卡

自动编码器的一个idea就是把高维度的数据（i.e.图像），编码到一个低维的隐空间中，使用的方法可能是如图的线性方法或者非线性的方法（i.e.深度全联通网络，卷积神经网络等等），可以简单地把这些方法看做一个函数，输入时图像$x$输出是隐空间内的编码$z$，这是一个编码（Encode）的的过程。

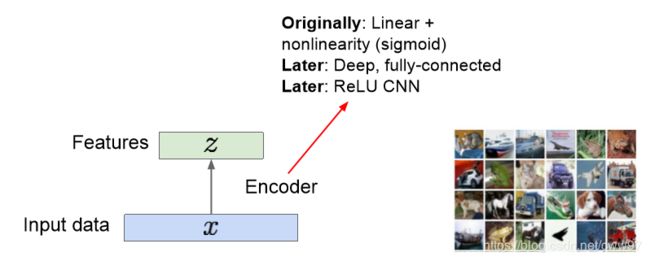
$z$通常是一个比原图像$x$尺寸小很多的一个向量，维度减少是因为隐空间里更多的存储了图像中有意义的信息（图像的特征）

那么现在问题来了，如果学习到这样一个学习图像特征的表示的方法呢？训练的特征应当可以用于还原出原始的图片，这就是所谓的“自动编码器”——编码自己

此时，训练这么一个编码器网络和一个解码器网络，$x$是原图像，$z$是隐空间中编码的向量， $\hat{x}$解码器还原出的图像。很容易写出的损失函数：

$$\mathcal{L}=||x-\hat{x}|{|}^2$$

自动编码器的训练过程主要在这里。训练结束之后，我们可以把解码器网络直接扔掉，没错，直接扔掉，想想看一些图像处理的任务，最简单的，图像分类，直接处理隐空间的图像特征信息是不是比直接处理图像简单很多。玩一些有监督的学习，分类器之类的工作，瞬间感觉舒服了许多是不是。

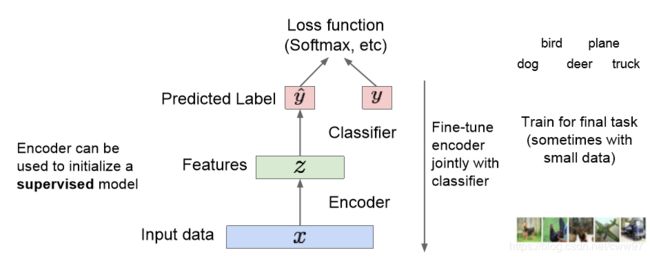
自动编码器可以还原出图像，可以学习到图像的特征信息用于初始化一个监督学习的模型。更进一步，我们能不能使用我们的编码的隐空间的图像的特征信息来生成一些新的本来不存在的图像呢

变分自动编码器

好了，现在我们的想法是想要一个生成模型。假设我们的训练数据 $\{x^{(i)}{\}}_{i=1}^N$是从隐空间的分布$z$中生成的

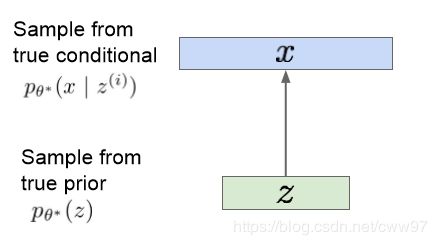
注意上图中 $x(i)$ 是一张图片，$z$是 隐空间中用于生成 $x$的变量。对于这样一个生成模型，我们想要估计$z$的真实分布的参数 $\theta$。该如何表示这个模型呢。

众所周知，万事万物很多东西都服从高斯分布，我们简单的将这个$z$假装它是个高斯分布（为什么可以这么假设？？？可能这就是高斯分布牛逼的地方了吧）。条件概率 $p(x|z)$是一个比较复杂的，从隐空间生成图片的一个神经网络，${\theta }^{\ast }$是这个网络的真实参数。

隐空间中的图片 $z$ 服从一个先验分布 $p_{{\theta }^{\ast }}(z)$，完美的解码器即为 $p_{{\theta }^{\ast }}(x|z^{(i)})$。现在的问题是如何训练这个 ${\theta }^{\ast }$。注意这是一个生成模型，我们最终的目标是生成$x$，那直接求$x$的最大似然：

$$p_{\theta }(x)=\int p_{\theta }(z)p_{\theta }(x|z)dz$$

这里的$p_{\theta }(z)$是一个简单的高斯分布，$p_{\theta }(x|z)$是解码器的神经网络，但是无法对所有 的$z$求积分。故此路不通，尝试使用贝叶斯公式：

$$p_{\theta }(x)=\frac{p_{\theta }(x|z)p_{\theta }(z)}{p_{\theta }(z|x)}$$

分子易得，则需要求$p_{\theta }(z|x)$：

$$p_{\theta }(z|x)=p_{\theta }(x|z)p_{\theta }(z)/p_{\theta }(x)$$

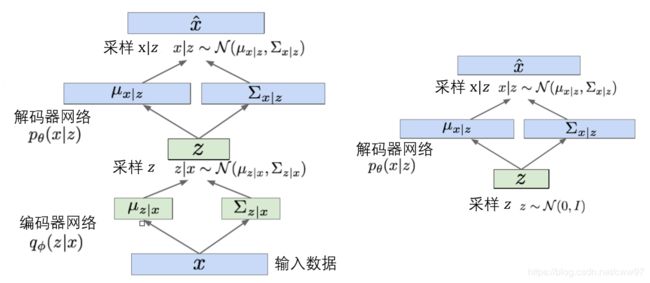
我们发现此处再一次出现了原问题$p_{\theta }(x)$，这已经是一个死循环了，必须有一些平如的操作才能继续算下去。引入一个额外的编码器 $q_{\varphi }(z|x)$来估计${\mathrm{p}}_{\theta }(\mathrm{z}|\mathrm{x})$，此时我们有图 \ref{vae_pq}中的两个网络：解码器网络记为$q_{\varphi }(z|x)$，编码器网络记为${\mathrm{p}}_{\theta }(\mathrm{z}|\mathrm{x})$。

此时对于个数据集$X$里的一张图片 $x^{(i)}$，我们可以求解$log$数据似然：

$$\begin{array}{rl}\log p_{\theta }\left(x^{(i)}\right)& ={\mathbf{E}}_{z\sim q_{\varphi }(z|x(i))}\left[\log p_{\theta }\left(x^{(i)}\right)\right]\left(p_{\theta }\left(x^{(i)}\right)\text{ 不依赖于 }z\right)\\ & ={\mathbf{E}}_z\left[\log \frac{p_{\theta }\left(x^{(i)}|z\right)p_{\theta }(z)}{p_{\theta }(z|x^{(i)})}\right]\left(贝叶斯公式\right)\\ & ={\mathbf{E}}_z\left[\log \frac{p_{\theta }\left(x^{(i)}|z\right)p_{\theta }(z)}{p_{\theta }(z|x^{(i)})}\frac{q_{\varphi }(z|x^{(i)})}{q_{\varphi }(z|x^{(i)})}\right]\left(乘一个常数\right)\\ & ={\mathbf{E}}_z\left[\log p_{\theta }\left(x^{(i)}|z\right)\right]-{\mathbf{E}}_z\left[\log \frac{q_{\varphi }(z|x^{(i)})}{p_{\theta }(z)}\right]+{\mathbf{E}}_z\left[\log \frac{q_{\varphi }(z|x^{(i)})}{p_{\theta }(z|x^{(i)})}\right]\left(log展开\right)\\ & ={\mathbf{E}}_z\left[\log p_{\theta }\left(x^{(i)}|z\right)\right]-D_{KL}\left(q_{\varphi }(z|x^{(i)})\Vert p_{\theta }(z)\right)+D_{KL}\left(q_{\varphi }(z|x^{(i)})\Vert p_{\theta }(z|x^{(i)})\right)\end{array}$$

这里第一项中的$p_{\theta }\left(x^{(i)}|z\right)$由解码器网络提供，$D_{KL}\left(q_{\varphi }(z|x^{(i)})\Vert p_{\theta }(z)\right)$则是编码器和$z$的先验分布（正态分布）的KL散度，最后一项包含$p_{\theta }(z|x^{(i)})$无法计算，但是我们知道任意的KL散度是非负的。所以我们领损失函数：

$$\mathcal{L}\left(x^{(i)},\theta ,\varphi \right)={\mathbf{E}}_z\left[\log p_{\theta }\left(x^{(i)}|z\right)\right]-D_{KL}\left(q_{\varphi }(z|x^{(i)})\Vert p_{\theta }(z)\right)$$

该式即为数据似然的下界，即：

$$\log p_{\theta }\left(x^{(i)}\right)\ge \mathcal{L}\left(x^{(i)},\theta ,\varphi \right)$$

所以我们的优化目标：

$${\theta }^{\ast },{\varphi }^{\ast }=\arg \underset{\theta ,\varphi }{\max }\sum _{i=1}^N\mathcal{L}\left(x^{(i)},\theta ,\varphi \right)$$

损失函数前一项为解码器，从隐空间中重新构造出了输入图像，后一项使得编码器与先验分布相似。此时我们的VAE的结构如图 \ref{vae_struct}中左图所示。右图展示了训练完成的VAE，VAE本质是一个生成模型，我们的$z$是服从高斯分布的，而任意高斯分布可以从$0$-$1$高斯分布转化而得。所以生成图片的过程等价于从$0$-$1$高斯分布中采样，这是VAE实现高效采样的根本原因。

Reference

• cs231n
• wiki-贝叶斯定理
• 极大似然估计详解
• wiki-相对熵

Appendix

草稿纸，推导过程