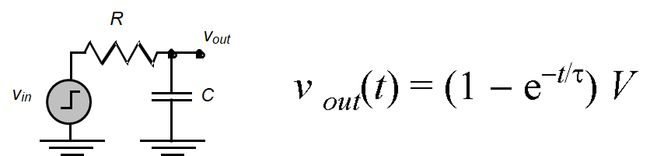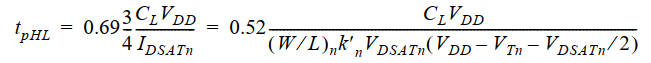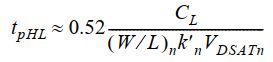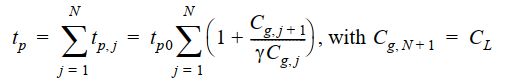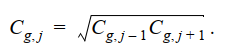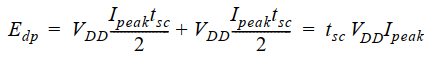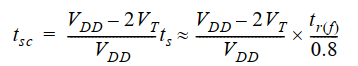专用集成电路 -- 反相器

专用集成电路 – 反相器

@(知识点汇总)

《数字集成电路–电路、系统与设计》第二版 复习笔记

[TOC]

Chapter 1

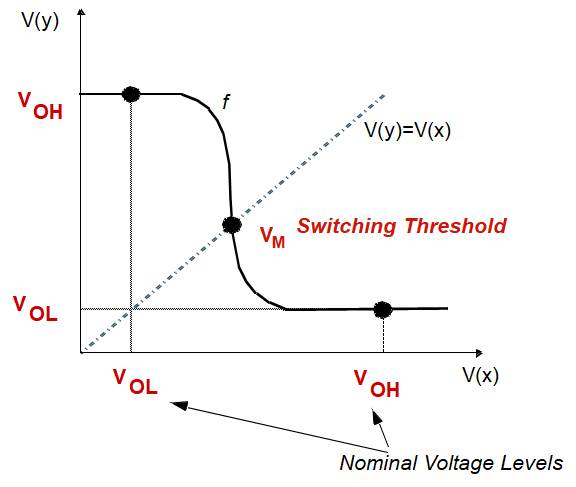
1.反相器的电压传输特性 （VTC)

• $V_{OH}$: 额定高电压
• $V_{OL}$ : 额定低电压
• $V_M$ : 门阈值电压（开关阈值电压，非晶体管VT）
  • 是$V_{out}=V_{in}$的点
  • 是开关特性的中点，在门的输出端短接到输入端得到

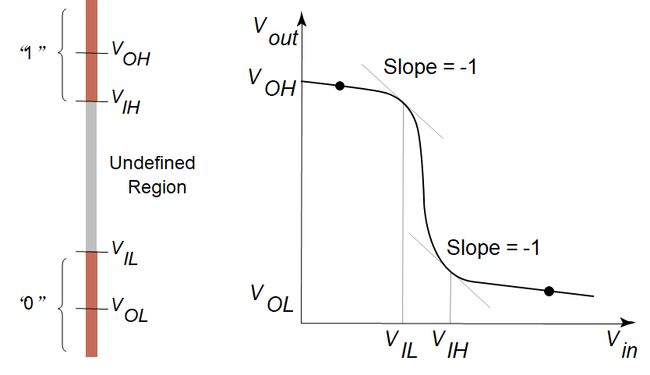
• $V_{IH}$: 可接受的高电压下限
• $V_{IL}$: 可接受的低电压上限
  • 这两个值都是在VTC增益（$d{V}_{out}/d{V}_{in}$)等于-1的点
• $V_{IH}-V_{IL}$: 不确定区域，或者叫过渡宽度（Transition Width, TW)

噪声容限：

• $N{M}_L$: 低电平噪声容限

• $N{M}_L=V_{IL}-V_{OL}$

• $N{M}_H$: 高电平噪声容限

  • $N{M}_H=V_{OH}-V_{IH}$

前级的输出在后级的噪声容限范围内是可以接收的。

再生性：

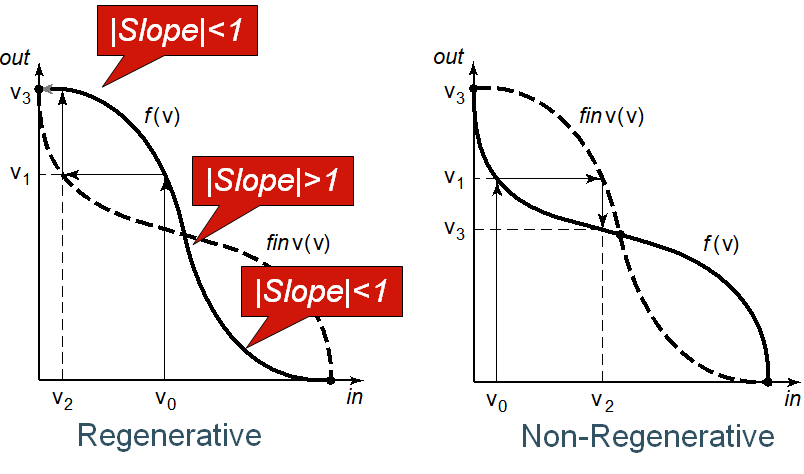
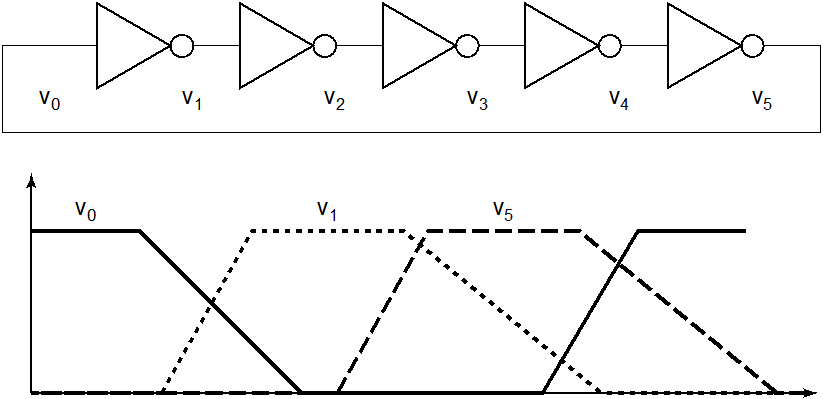
要保证多级反向器级联以后，输出能趋向于逻辑电平，需要保证反向器链满足再生性：过渡区增益绝对值大于1，合法区增益绝对值小于1

V0的输出接到V1的输入，如果这些反向器都相同，他们的VTC都一样，只是输入和输出对调位置。考察反向器链，他们的VTC组合图如上面。如果满足再生性，则V0-V1-V2…的输出会越来越趋近VOH。反之，不满足再生性（右图），则输出趋近VTC交点。

扇入和扇出：

• 扇出表示连接到驱动门输出的负载门数目。

  • 增加扇出会影响其逻辑输出电平（因为扇出电流*输出电阻将分掉一部分输出电压），通过使扇出负载门的输入电阻尽可能大（输入电流最小），并保持驱动门的输出电阻较小（减小负载电流对输出电压的影响）可以减小这一影响。
  • 负载门过多影响驱动门动态性能，因此库单元定义了最大扇出数

• 扇入

  • 大扇入会使静态和动态特性都变差

2. 数字电路的性能

• 性能： 数字电路的计算能力，经常用时钟频率衡量（能跑多快）

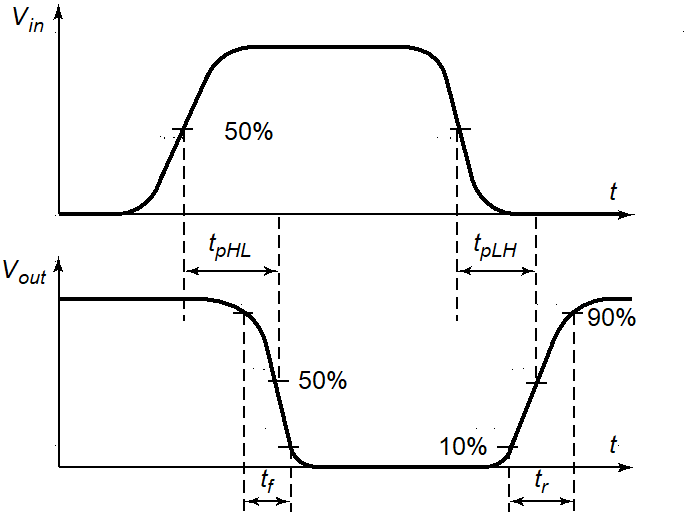
• 门的传播延时：$t_p$， 定义为输入和输出波形50%(假设VM是开关中点）翻转点之间的时间

• $t_{pLH}$ : 输出由低到高翻转的响应时间（跟输入也有关，不是单纯的输出低到高的时间）

• $t_{pHL}$ : 输出由高到低翻转的响应时间

• 传播延时$t_p=\frac{t_{pLH}+t_{pHL}}{2}$

• 传播延时与门的输入输出信号斜率有关，而上升下降延时只是针对单个波形，而非门。
• $t_r$ : 上升时间 10%-90%
• $t_f$ : 下降时间
• 取决于驱动门的强度和它所承受的负载

3. 环振

• 振荡周期$T=2\ast t_p\ast N$ ，其中 $N$是级数。
• 起振条件：$2N{t}_p>>t_f+t_r$
• 一般至少要5级才能工作。

4. 一阶RC网络

一般反相器可以模拟成如下的一阶RC网络，当输入加上一个阶跃信号（Vin从0到V)

• $\tau =RC$
• Vout达到50%时，$t=ln(2)\tau =0.69RC$, 这里输入的tr为0，所以 $t_p=0.69RC$
• 输出$t_f=ln(9)\tau =2.2RC$

5. 功耗

$Power_Delay_Product (PDP) =
Energy_per_operation = P_{av}*t_p $

$Energy_Delay_Product (EDP) =
quality_metric_of_gate = E*t_p $

一阶RC网络的能耗

当加上阶跃信号（0-V),信号源从过渡开始到结束，输入的总能量为：

可以看到，对于阶跃输入，使电容从0充电到V需要的能量和电容大小和电压有关，与电阻无关。

同样，从过渡结束时有下面这么多能量存储在电容上：

另一半的能量消耗在了电阻上。

同样，在放电时（一个V至0的阶跃），存储在电容上的能量也通过电阻变为热能。

Chapter 5

1. CMOS反向器的VTC曲线

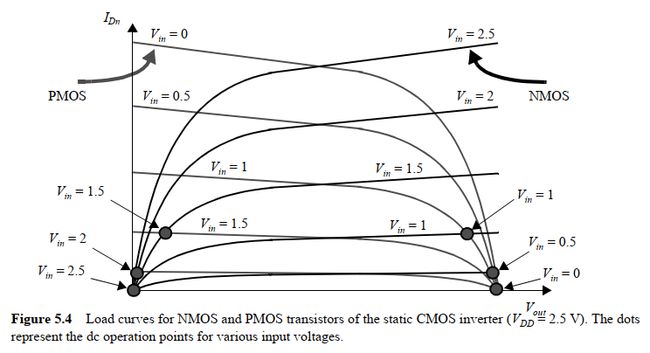
通过将PMOS管Ids和Vds特性曲线转换到NMOS管的坐标中，可以得到如下曲线：

### 2. 静态特性 #### 2.1 开关阈值

开关阈值$V_M$定义为$V_{in}=V_{out}$的点，在该区域$V_{GS}=V_{DS}$,因此PMOS和NMOS总是饱和的。
通过电流相等的关系联立P和N的速度饱和区方程可以得到$V_M$:
$$V_M=\frac{r{V}_{DD}}{1+r},r=\frac{v_{satp}{W}_p}{v_{satn}{W}_n}$$

• r是P管和N管的相对驱动强度比。一般希望开关阈值在电压摆幅中点，（以便获得相同的噪声容限）也就是VDD/2处，因此要求r=1，也就是P和N的驱动强度相等。
• 同时，增大P管驱动强度（加大p管宽长比）将使开关阈值大于VDD/2（上漂）；增大N管驱动强度则开关阈值下移。

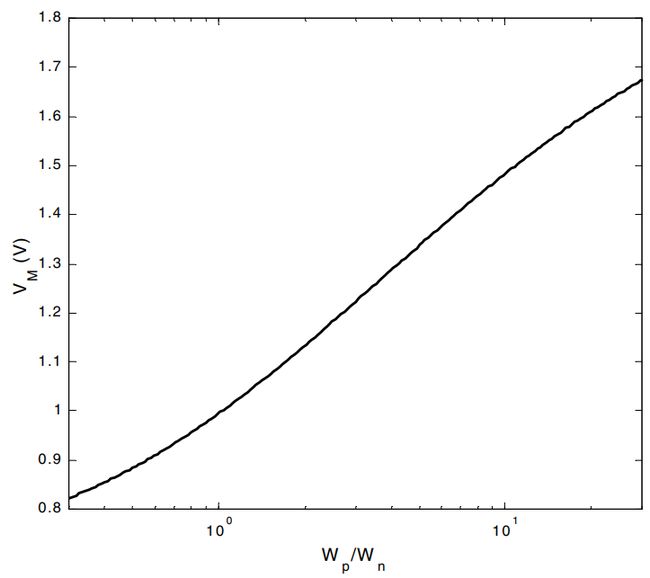
$V_M$可以表示为P管和N管的宽长比的函数，VDD=2.5：

当$V_M=1.25$时，通过公式计算得到的P和N宽长比之比为3.5

• 通过曲线可以发现，$V_M$对宽长比的变化相对来说是不敏感的，因此实际工艺生产中并不要求P管宽度等于完全对称时的宽度。
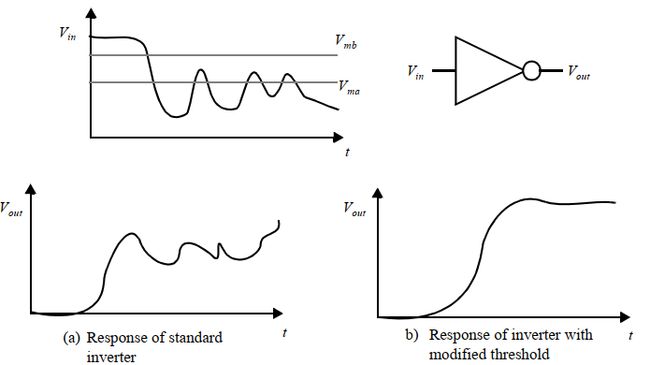
• 通过增加P或N的宽度可以使得开关阈值上移或下移，这种不对称的传输特性在设计时非常有用。比如下图通过调整阈值使得原本对输入噪声敏感的反相器变得不那么敏感：

2.2 噪声容限

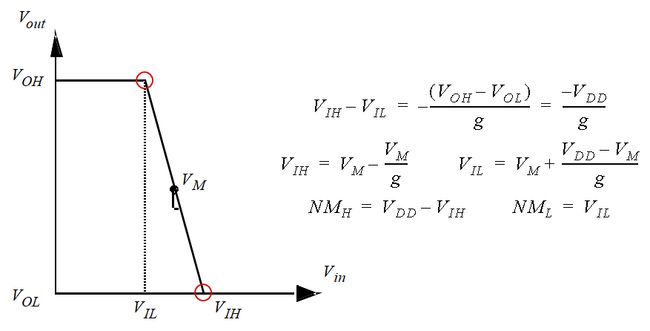
VIL和VIH需要计算VTC的增益g=-1的点，不过还有一种简化的噪声容限可以用下面的公式表示，相当于将过渡区线性近似。

当然，使用上述近似得到的噪声容限是比较乐观的。

4. 增益曲线

通过求解VTC曲线的梯度可以得到增益g关于输入的曲线：

可以发现：

• 静态CMOS反相器也可以作为一个模拟放大器使用，在过渡区会有相当高的增益。但是这一区域很窄，作为放大器的一些其他性质也很差。
• 可见模拟和数字设计的差异：
  • 模拟设计会把放大器偏置在过渡区中点获得最大的线性度
  • 而数字设计则将其工作在极端的非线性区域，得到明确和分离很号的高低电平

2.3 鲁棒性

器件在不同的制造工艺（Process),工作电压（Voltage)以及温度（Temperature)条件下其参数一定会偏离设计中采用的典型值，但静态CMOS反相器的dc特性对这些变化不敏感，所以可以在很宽的工作条件下正确工作，这也是静态CMOS门普遍使用的主要原因。

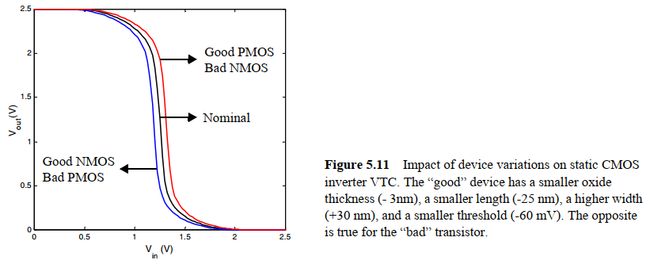
下图显示了器件参数变化对VTC的影响：

可见，好的PMOS使开关阈值上移动，差的NMOS使其下移，但无论哪种其正常工作没有受到影响。

2.4 降低电源电压的影响

现代工艺尺寸连续缩小迫使电源电压和器件尺寸也按比例降低。但是器件的阈值电压却保持不变。
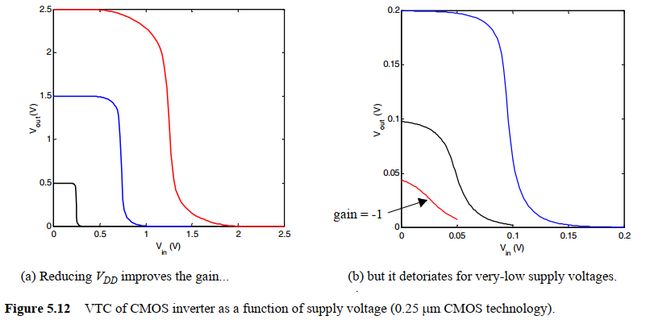
从增益公式可以发现，电压降低会使得过渡区增益增大！并且仍能正常工作（这不是非常好，可以改善dc特性，接近理想的反相器）如图：

但是在接近阈值电压的VDD下工作会有诸多问题：

1. 虽然降低电压能减少功耗，但绝对会使门的延时增大。
2. 一旦电源电压接近阈值电压，dc特性对器件参数（比如阈值）的波动将变得越发敏感（降低了鲁棒性）。
3. 降电压意味着减少信号摆幅，虽然能抑制系统内部噪声，比如串扰，但是对外部不变的噪声将更加敏感。

上图中右边图展示了在非常低的电压下的工作曲线，可以发现在低于阈值电压的VDD下电路仍能得到反相器的特性，这实际上处于晶体管的亚阈值工作区，亚阈值电流足以使门在高低电平之间转换，并得到可接受的VTC.
但这么小的电流值决定了反相器工作非常慢，不过在特殊场景下也可以接受（比如手表）

3. 动态特性

3.1 传播延时

要精确求解反相器延时需要对电容充放电电流积分，是难以求解的。但是可以通过另一种方式近似，也就是求等效导通电阻转化为一阶RC模型。
MOS管的平均导通电阻为：

对于一个电压阶跃激励，可以求得传播延时：
$$t_{pHL}=0.69R_{eqN}{C}_L,t_{pLH}=0.69R_{eqP}{C}_L$$
$$t_p=\frac{t_{pHL}+t_{pLH}}{2}$$

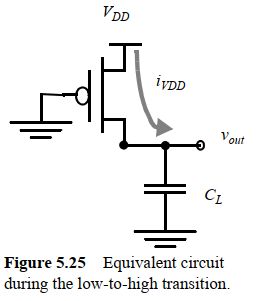
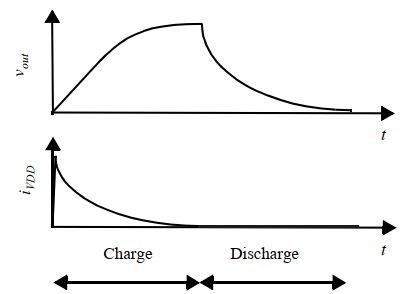
下图展示了一个模拟得到的反相器阶跃响应输出曲线：

由于存在栅极到漏极的电容，所以阶跃开始时就会把输入节点上的阶跃信号耦合到输出，导致了图中的尖峰（过充）。

对于更精确的传播延时，需要带入等效电阻公式：

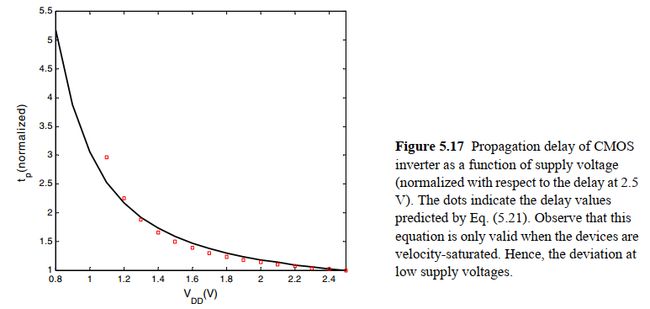
可以发现，当电源电压足够大时，传播延时几乎和电源电压无关，因为公式化简为：

下图展示了VDD和传播延时的关系，可以发现，当VDD较大时，传播延时变化不明显，或者说提高电源电压能带来很小的性能改善。而当电源电压小于$2V_T$时，延时迅速增加。

因此，减小门延时可以从如下几个方面考虑：

• 减小$C_L$:包括三部分电容：门本身内部扩散电容，互连线电容和扇出电容
• 增加晶体管宽长比：提高晶体管的驱动强度，但是也会增加本身的扩散电容（本征电容），当增加的扩散电容开始超过连线和扇出形成外部负载，增加门就不再对延时有贡献，这也被叫做$自载效应$。
• 提高VDD：会增加功耗，并且到一定程度后改善非常有限。

3.2 实际设计中的传播延时

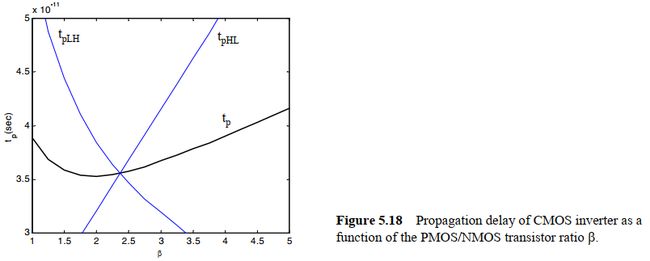
器件尺寸比$\beta =\frac{W/L_p}{W/L_n}$对传播延时也有较大影响，如图：

可以发现在$\beta$比值为1.9时,总的延时最小。
进一步分析延时的组成：
$$t_p=0.69R_{eq}(C_{int}+C_{ext})$$
$$=0.69R_{eq}{C}_{int}(1+C_{ext}/C_{int}）=t_{p0}(1+C_{ext}/C_{int})$$
其中，$C_{int}$是本征电容，$t_{p0}$是本征延时。表示器件在不加负载时的延时。本征延时跟门的尺寸无关。
增大器件尺寸实际上会增大本征电容，进而减小本征延时，但是会增加硅面积。
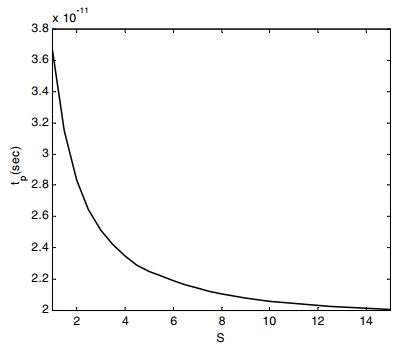
定义尺寸系数S,表示反相器跟标准反相器的尺寸比，则$C_{int}=S{C}_{iref},R_{eq}=R_{ref}/S$,S会影响传播延时：

可以发现，最大的性能改善约为2（1.9），当S大于5时，延时已经得到了较大改善，再增大得到的收益很有限。

3.3 确定反相器链的尺寸

增大尺寸可以减小延时，但也增加了输入电容，当门处于实际环境时如何确定尺寸呢？简单的反相器链是最好的研究起点。
首先反相器的输入栅极电容$C_g$与本征输出电容的关系可以写为：
$$C_{int}=\gamma C_g$$
对于大多数亚微米工艺$\gamma$接近1，延时公式可以重写为：
$$t_p=t_{p0}(1+f/\gamma )$$
其中$f=C_{ext}/C_g$为等效扇出。对于一个反相器链：

可以得到最终的输出延时公式为各级延时之和：

要使最后的总延时最小，根据公式可以得到需要每一级的等效扇出相等，也就是需要每级的栅电容是前后的算数平均，假设$F=C_L/C_{g.1}$为总等效扇出，则有：

最后的延时可以表示为：

那么如何选择一个反相器链的正确级数呢？
对于给定的F，再选择级数时，如果级数比较大，则通过对延时求导可以得到最优的级数,在忽略自载时（$\gamma =0$)时有收敛解：
$$N=ln(F)，且每一级的等效扇出f=e.$$
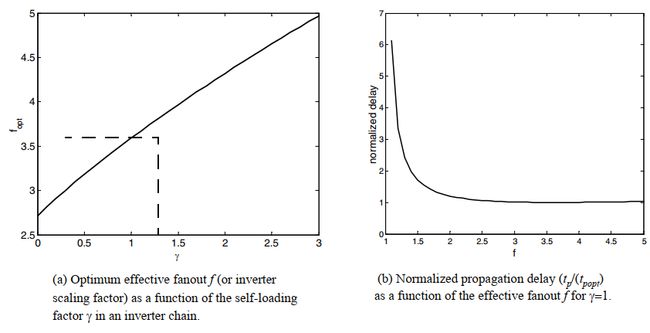
左图表示了等效扇出与自载系数的关系，右图表示$\gamma =1$时的延时和等效扇出的关系：

可见，$\gamma = 1$时，最优的f=3.6,选择稍大的f不会过多影响延时，但可以减少缓冲器级数和面积，通常选择最优扇出为4.过多的级数会使得f小于最优值，增大延时。

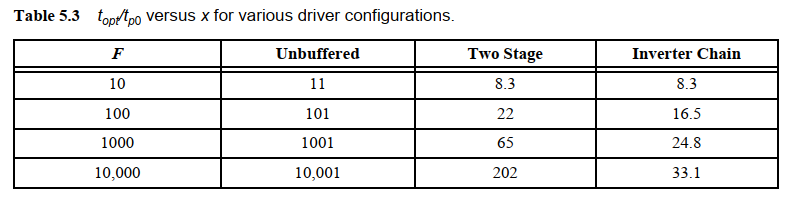
反相器链可以加速驱动大负载的延时：
下表展示了无缓冲器，两级反相器以及反相器链在驱动特定负载时的归一化延时：

可见，反相器链相比于直接驱动可以极大地减小延时。

4. 功耗、能量和能量延时

4.1 动态功耗

a.电容充放电功耗（开关功耗）

在第一章已经讨论过，MOS管的充放电功耗。充电和放电消耗的总能量为：$C_L{V}_{DD}^2$,其中有一半消耗在P管上，另一半存储在电容上。在放电时这部分能量通过N管消耗掉。
因此这部分动态功耗取决于开关活动性（每个周期翻转多少次）：
$$P_{dyn}=C_L{V}_{DD}{f}_{0->1}$$
其中，$f_{0->1}$可以表示为一段时间内的翻转次数乘上频率。

---

确定晶体管尺寸使得能耗最小：
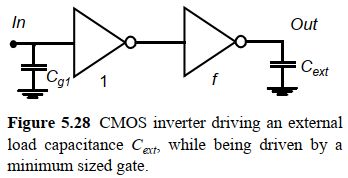
下图是一个静态反相器驱动外部负载的情形。为考虑负载效应，假设反相器本身被一个最小尺寸器件驱动。目的是使整个电路能耗最小且保持最低性能指标。设计参数是VDD和f。优化的约束是其性能应该和f=1,VDD=Vref的参考电路相当。

通过传播延时的约束$t_p=t_{pref}$可以得到f和VDD的约束关系，如上面的左图所示。同时根据左图以及动态功耗公式可以得到右图f和功耗的关系。
左边图很好理解，由最小f=1增加尺寸会使性能提高，因此可以降电压来降低功耗，但当f达到最优解$f=\sqrt{F}$(N=2)后，再加大尺寸会增加自载效应，必须提高电压来弥补性能损失。
通过上图可以发现：

• 改变器件尺寸并降低电压可以有效减少能耗。对于较大扇出F的电路尤其明显。
• 在最优f之外过多增大尺寸会付出较大的能量代价。
• 能量的最优f通常小于考虑性能的最优f。

b. 直流通路功耗（短路功耗）

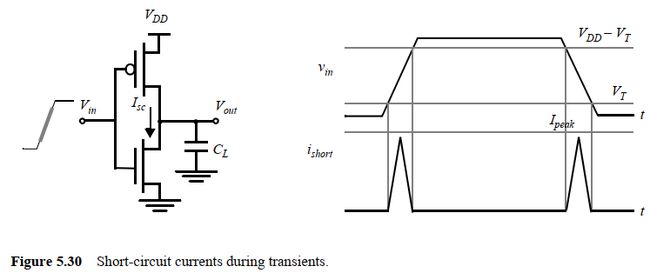
输入波形存在上升和下降时间，导致在开关过程中形成直流通路，造成短路电流。假设脉冲电流可以近似为三角形，如下图：

则可以计算其能量为：

对应的平均功耗$P_{dp}$: $$ \color{red}{P_{dp}=t_{sc}V_{DD}I_{peak}f_{0->1}=C_{sc}V_{DD}^2f_{0->1}} $$ $C_{sc}$可以看作一个和CL并联的电容，用来模拟短路功耗。 直流通路引起的功耗和**开关活动性**成正比。其中$t_{sc}$表示导通时间，和VT有关：

下面考察峰值电流$I_{peak}$的情况：

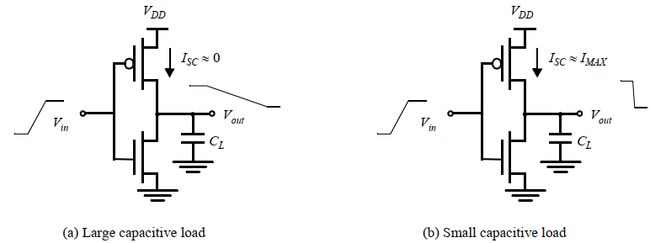
• 当负载很大，RC常数大，输出端变化很慢，所以输出的下降时间明显比输入上升时间大，输出在改变之前P管VDS就基本为0，P管就基本关断了，所以$I_{peak}$很小
• 反之，当负载很小，输出下降时间明显小于输入上升时间，PMOS的VDS大部分时间等于VDD,所以导致了最大的短路电流（PMOS的饱和电流）。
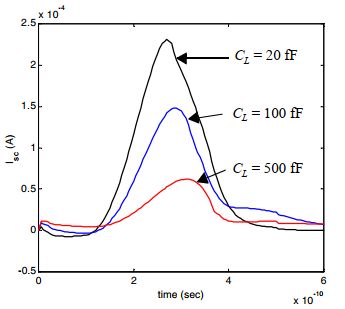
  下图展示了输出电容跟短路电流的关系：

可以发现，使输出的上升下降时间大于输入上升下降时间可以减小短路功耗，但输出的上升下降时间太大会降低性能，并在扇出门中引起短路电流。可见局部优化是不行的。
从全局角度优化短路功耗：
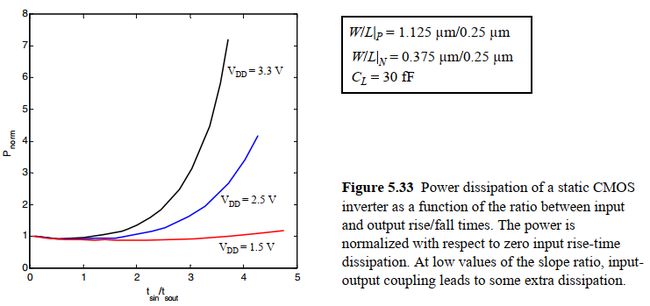
单个门的输入和输出上升下降时间相等对这个门来说不是最优的结果，但是能保持整个电路的短路电流在一定范围内。下图是一个反相器的功耗与输入输出上升下降时间之比的关系曲线。

可以看到：

• 当负载电容比较小时，短路功耗将占主导，而当负载电容较大时，功耗都用来充放电负载。
• 如果使得输入输出上升下降时间相等，则大部分功耗与开关功耗也就是充放电功耗有关。只有很小（<10%)一部分来自短路电流。
• 当电压降低到VDD

4.2 静态功耗

静态功耗可以表示为：
$$P_{stat}=I_{stat}VDD$$
也就是在没有开关活动时存在电源到地的电流。
正常情况下P和N在正常工作下不会同时导通，但总会有如下形式的泄露电流：

1. 源或漏与衬底之间的反偏二极管漏电（结的泄露电流）
   • 通常情况下非常小，但该部分漏电是由热产生的载流子引起的，当结温上升时，结漏电指数上升。
   • 解决办法：限制电路功耗或者使用有效散热的封装
2. 亚阈值电流。
   • VGS接近阈值电压时会有源漏电流，在深亚微米工艺下，电源电压降低导致这一电流越发显著。
   • 解决办法：保持较高的阈值电压。但在现代工艺，保持阈值不变而降低电压会导致严重的性能损失。因此必须要在可接受的亚阈值漏电的前提下同步降低阈值电压，这就形成了性能和静态功耗之间的权衡取舍
   • 下图展示了阈值电压降低后亚阈值漏电增大的原因：

3. 栅极泄露电流。
   • 栅极采样了较薄的绝缘层，栅极电子可能发生量子隧穿通过栅氧化层到达源或漏，导致泄露电流。

注：具体降低动态和静态功耗的方法可以看Synopsys UPF文档。