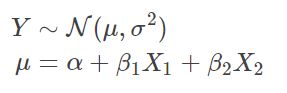贝叶斯学习笔记

概率编程允许在用户自定义的概率模型上进行自动贝叶斯推断。

本文主要基于概率编程的一个常用框架——PyMC3进行操作。PyMC3使用Theano通过变分推理进行梯度计算，并使用了C实现加速运算。PyMC3具有先进的下一代MCMC采样算法如No-U-Turn Sampler (NUTS; Hoffman, 2014)和Hamiltonian Monte Carlo自整定变体(HMC; Duane, 1987)。这类采样算法在高维和复杂的后验分布上具有良好的效果，允许对复杂模型进行拟合而不需要对拟合算法有特殊的了解。NUTS和HMC算法从似然函数中获得梯度信息，因此其收敛速度比传统采样方法快很多，特别是针对大模型。

预备知识

1、各种分布的基本特点：指数分布、Beta分布、Gamma分布等常见分布。其中Beta分布具有处于0~1之间，适合表征概率参数的概率分布（如抛硬币正面朝上的概率p的概率分布）。

2、离散分布的PMF、连续分布的PDF，以及CDF。

推荐另一个值得一读的博客：浅谈贝叶斯和MCMC

 

案例1：贝叶斯线性回归

本案例来自：PyMC3 - 简介和入门、Getting started with PyMC3

对于线性回归，频率学派采用最小二乘法等方法求解系数，那么贝叶斯学派怎么思考这个问题呢？

考虑一个简单的贝叶斯线性回归模型，其参数具有正态分布（Normal）先验。我们预测的具有正态分布的观测值 Y ，其期望 μ 是两个预测变量（X1、X2）的线性组合：

      

其中 α 是截距， βi 是变量 Xi 的系数； σ 代表观察误差。

建立贝叶斯模型，模型中的未知变量需要赋予先验分布，这里选择零均值的正态先验。其中，系数 α 、 βi 的方差为100，代表参数的弱信息。选择半正态分布作为观测误差 σ 的先验分布（半正态分布以0为边界的、形态为正态分布的一半）。

      

代码：

import numpy as np
import matplotlib.pyplot as plt
import pymc3 as pm

# 模拟观察数据
np.random.seed(123)

alpha=1
sigma=1
beta =[1, 2.5]

N=100

X1=np.random.randn(N)
X2=np.random.randn(N)

Y=alpha + beta[0]*X1 + beta[1]*X2 + np.random.randn(N)*sigma

# 建立贝叶斯模型
basic_model = pm.Model()
with basic_model:

    # 设置各参数的先验信息，使用随机变量（stochastic）
    alpha=pm.Normal('alpha',mu=0,sd=10)
    beta=pm.Normal('beta',mu=0,sd=10,shape=2)
    sigma=pm.HalfNormal('sigma',sd=1)

    # 构建线性回归关系，使用确定性变量（deterministic）
    mu=alpha+beta[0]*X1+beta[1]*X2

    # 设置Y的先验，并加入Y的观察数据
    Y_obs=pm.Normal('Y_obs',mu=mu,sd=sigma,observed=Y)

    ## 采样推断模型参数
    # 用MAP获得初始点
    start = pm.find_MAP(fmin=optimize.fmin_powell)

    # 实例化采样器
    step = pm.Slice(vars=[sigma])

    # 对后验分布进行5000次采样
    trace = pm.sample(5000, step=step,start=start)

说明：

为了使用MCMC采样以获得后验分布的样本，PyMC3需要指定和特定MCMC算法相关的步进方法（采样方法）,如Metropolis, Slice sampling, or the No-U-Turn Sampler (NUTS)。PyMC3中的 step_methods 子模块提供了如下采样器： NUTS, Metropolis, Slice, HamiltonianMC, and BinaryMetropolis。可以由PyMC3自动指定也可以手动指定。自动指定是根据模型中的变量类型决定的：
* 二值变量：指定 BinaryMetropolis
* 离散变量：指定 Metropolis
* 连续变量：指定 NUTS

 

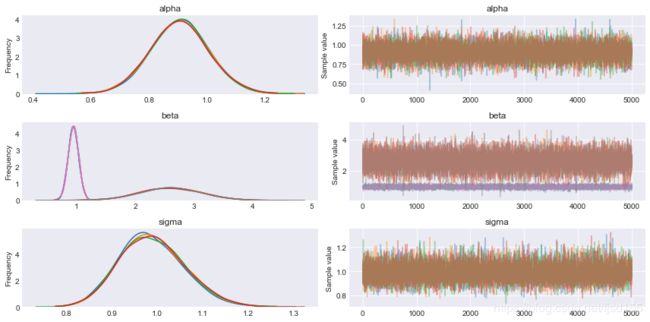
PyMC3提供了 traceplot 函数来绘制后验采样的趋势图。

pm.traceplot(trace)

      

 

案例2：贝叶斯A/B测试

摘自：Bayesian Methods for Hackers: Probabilistic Programming and Bayesian Inference

有一批关于A药和B药治疗某种疾病的数据（是否治愈），我们想知道两个药的治愈率哪个更高。假定药物治愈该疾病服从伯努利分布。频率学派常采用 t 检验等方法进行测试，那么贝叶斯学派又是如何测试呢？

代码：

import pymc3 as pm
figsize(12, 4)

# 真实值，但现实情况中我们并不知道
true_p_A = 0.05
true_p_B = 0.04

# notice the unequal sample sizes -- no problem in Bayesian analysis.
N_A = 1500
N_B = 750

# 模拟观察数据
observations_A = stats.bernoulli.rvs(true_p_A, size=N_A)
observations_B = stats.bernoulli.rvs(true_p_B, size=N_B)

# 贝叶斯建模推断
with pm.Model() as model:

    # 设置先验
    p_A = pm.Uniform("p_A", 0, 1)
    p_B = pm.Uniform("p_B", 0, 1)
    
    # Define the deterministic delta function. This is our unknown of interest.
    delta = pm.Deterministic("delta", p_A - p_B)

    
    # Set of observations, in this case we have two observation datasets.
    obs_A = pm.Bernoulli("obs_A", p_A, observed=observations_A)
    obs_B = pm.Bernoulli("obs_B", p_B, observed=observations_B)

    # 设置step方法，采样后丢弃前1000样本（burn策略）
    step = pm.Metropolis()
    trace = pm.sample(20000, step=step)
    burned_trace=trace[1000:]

p_A_samples = burned_trace["p_A"]
p_B_samples = burned_trace["p_B"]
delta_samples = burned_trace["delta"]

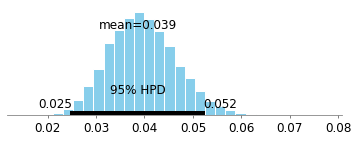
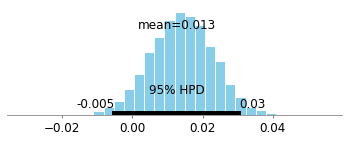
pm.plots.plot_posterior(trace=p_A_samples)
pm.plots.plot_posterior(trace=p_B_samples)
pm.plots.plot_posterior(trace=delta_samples)

print("Probability site A is BETTER than site B: %.3f" % \
    np.mean(delta_samples > 0))

      

      

      Probability site A is BETTER than site B: 0.918

 

案例3：抛硬币与共轭分布

这是一个极其简单的例子，此处举例主要是为了引出“共轭分布”的概念。

我们都知道抛硬币正面朝上的概率为0.5（硬币没被做手脚的情况下，并且本案例也默认真实概率为0.5），频率学派直接用频率推断概率。那么贝叶斯学派是怎么推断这个概率的呢？贝叶斯学派先要假定一个先验概率，我们假定先验知识为：正面朝上的概率服从0~1之间的均匀分布（我们一无所知），随着抛硬币实验结果一个个出现，我们用实验结果逐步更新后验概率。代码如下

%matplotlib inline
from IPython.core.pylabtools import figsize
import numpy as np
from matplotlib import pyplot as plt
figsize(11, 9)

import scipy.stats as stats

dist = stats.beta
n_trials = [0, 1, 2, 3, 4, 5, 8, 15, 50, 500]
data = stats.bernoulli.rvs(0.5, size=n_trials[-1])
x = np.linspace(0, 1, 100)

# For the already prepared, I'm using Binomial's conj. prior.
for k, N in enumerate(n_trials):
    sx = plt.subplot(len(n_trials)/2, 2, k+1)
    plt.xlabel("$p$, probability of heads") \
        if k in [0, len(n_trials)-1] else None
    plt.setp(sx.get_yticklabels(), visible=False)
    heads = data[:N].sum()
    y = dist.pdf(x, 1 + heads, 1 + N - heads)
    plt.plot(x, y, label="observe %d tosses,\n %d heads" % (N, heads))
    plt.fill_between(x, 0, y, color="#348ABD", alpha=0.4)
    plt.vlines(0.5, 0, 4, color="k", linestyles="--", lw=1)

    leg = plt.legend()
    leg.get_frame().set_alpha(0.4)
    plt.autoscale(tight=True)


plt.suptitle("Bayesian updating of posterior probabilities",
             y=1.02,
             fontsize=14)

plt.tight_layout()

      

注意到，我们直接使用公式更新了概率分布，而不是每次都进行MCMC采样推断。这个公式利用了一个重要的原理：

一个Beta先验分布连同二项式生成的观测数据将形成一个Beta后验分布。即：

若 p~Beta(α, β)，且 X~Binomial(N, p)，则 p|X ~ Beta(α+X, β+N-X) 。

注意：均匀分布等价于Beta(1, 1)，即服从Beta分布 。

我们称Beta分布是二项分布的共轭分布。更多的共轭分布，可以查看维基百科的共轭先验表。比如Dirichlet 分布是多项式分布的共轭分布（Beta分布和二项式分布的多维推广）。对于简单的一维问题，可以尝试这种方法。但是，对于复杂的问题，往往很难利用共轭分布这个技巧，MCMC采样推断仍然是最重要的。

需要强调的是，对于一个基本贝叶斯推断问题，至少存在2个分布类型需要设置：所需估计的参数的先验分布，观察数据的分布。先验分布根据经验进行设定，可以存在一定的主观性，先验的分布类型选错了也不会导致特别大的问题（一般情况下）；观察数据的分布，是真正的贝叶斯模型，是观察数据产生的框架，分布类型如果没选好，模型也就难以拟合。贝叶斯推断，是基于这个假定的模型框架，根据观察数据去推断这个模型框架的各个参数值。在贝叶斯推断里，复杂的变换可以通过建立逻辑关系映射到最终的因变量，然后为因变量选定分布类型，使得观察数据的产生服从这个分布类型。

 

案例4：概率质量函数推断似然函数

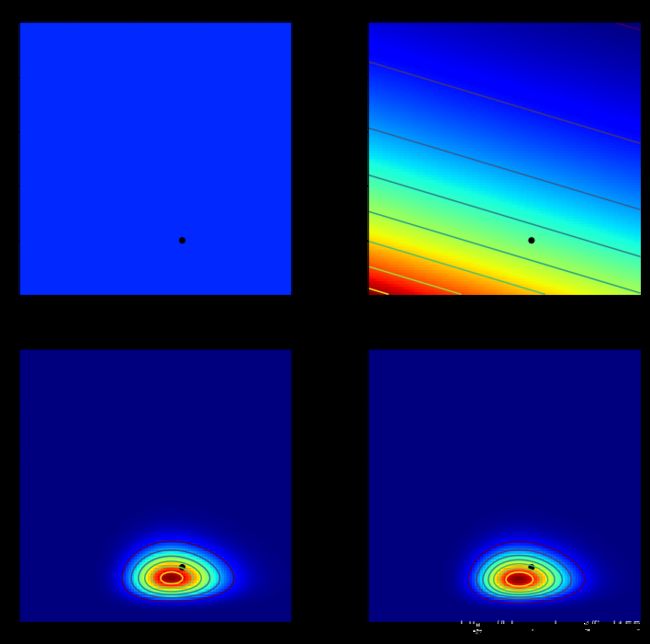
Poisson分布的概率质量函数在参数 lambda 处取得最大值（这一点不容忽视）。假设当前假定的lambda值为b（所有可能的lambda值通过枚举产生），利用观察数据a和模拟的 lambda值b 可以求出观察数据a处的概率密度值；若有多个观察数据，则可将多个概率密度值累乘，从而估算出参数b为真实lambda值的可能性。将这个可能性与先验分布相乘，则可得到后验分布。

%matplotlib inline
import scipy.stats as stats
from IPython.core.pylabtools import figsize
import numpy as np

import matplotlib.pyplot as plt

jet = plt.cm.jet

# sample size of data we observe, trying varying this (keep it less than 100 ;)
N = 10

# the true parameters, but of course we do not see these values...
lambda_1_true = 1
lambda_2_true = 3

#...we see the data generated, dependent on the above two values.
data = np.concatenate([
    stats.poisson.rvs(lambda_1_true, size=(N, 1)),
    stats.poisson.rvs(lambda_2_true, size=(N, 1))
], axis=1)
print("observed (2-dimensional,sample size = %d):" % N, data)

# plotting details.
x = y = np.linspace(.01, 5, 100)
likelihood_x = np.array([stats.poisson.pmf(data[:, 0], _x)
                        for _x in x]).prod(axis=1)
likelihood_y = np.array([stats.poisson.pmf(data[:, 1], _y)
                        for _y in y]).prod(axis=1)
L = np.dot(likelihood_x[:, None], likelihood_y[None, :])

figsize(12.5, 12)
# matplotlib heavy lifting below, beware!
plt.subplot(221)
uni_x = stats.uniform.pdf(x, loc=0, scale=5)
uni_y = stats.uniform.pdf(x, loc=0, scale=5)
M = np.dot(uni_x[:, None], uni_y[None, :])
im = plt.imshow(M, interpolation='none', origin='lower',
                cmap=jet, vmax=1, vmin=-.15, extent=(0, 5, 0, 5))
plt.scatter(lambda_2_true, lambda_1_true, c="k", s=50, edgecolor="none")
plt.xlim(0, 5)
plt.ylim(0, 5)
plt.title("Landscape formed by Uniform priors on $p_1, p_2$.")

plt.subplot(223)
plt.contour(x, y, M * L)
im = plt.imshow(M * L, interpolation='none', origin='lower',
                cmap=jet, extent=(0, 5, 0, 5))
plt.title("Landscape warped by %d data observation;\n Uniform priors on $p_1, p_2$." % N)
plt.scatter(lambda_2_true, lambda_1_true, c="k", s=50, edgecolor="none")
plt.xlim(0, 5)
plt.ylim(0, 5)

plt.subplot(222)
exp_x = stats.expon.pdf(x, loc=0, scale=3)
exp_y = stats.expon.pdf(x, loc=0, scale=10)
M = np.dot(exp_x[:, None], exp_y[None, :])

plt.contour(x, y, M)
im = plt.imshow(M, interpolation='none', origin='lower',
                cmap=jet, extent=(0, 5, 0, 5))
plt.scatter(lambda_2_true, lambda_1_true, c="k", s=50, edgecolor="none")
plt.xlim(0, 5)
plt.ylim(0, 5)
plt.title("Landscape formed by Exponential priors on $p_1, p_2$.")

plt.subplot(224)
# This is the likelihood times prior, that results in the posterior.
plt.contour(x, y, M * L)
im = plt.imshow(M * L, interpolation='none', origin='lower',
                cmap=jet, extent=(0, 5, 0, 5))

plt.scatter(lambda_2_true, lambda_1_true, c="k", s=50, edgecolor="none")
plt.title("Landscape warped by %d data observation;\n Exponential priors on \
$p_1, p_2$." % N)
plt.xlim(0, 5)
plt.ylim(0, 5)

      

 

补充知识

理性使用MCMC采样点

1、MCMC采样点的初期阶段，采样不够成熟，可考虑舍弃初期预热的采样点，即采用burn策略；此外，可以利用MAP方法（包括fmin、Powell等方法）设定MCMC的起点来缩短预热期。

2、MCMC采样具有自相关性（不容忽视的概念），为了保证采样的独立性，可考虑进行稀释（每隔K个点纳入最终分析）。

 

贝叶斯建模的基本思路

我们拿到一堆观察数据，思考这些数据是如何产生的是进行贝叶斯建模的不错的开始。

1、什么样的随机变量最可能产生这些观察数据？也就是说，我们需要选定一个分布类型。

2、所选定的分布类型，需要哪些参数？这些参数又是怎么产生的？比如某些参数服从某种分布，比如某些参数是其他参数推导来的。如果需要的参数服从某种分布，那么那种分布又需要哪些参数来构建？

3、重复2的思考，直到可以放心地设置某个参数的先验分布。

总结一下：贝叶斯建模的关键在于，理解观察数据产生的随机规律（分布类型）（对应于概率模型），感知参数产生的规律（对应于先验分布），归纳参数之间的逻辑规律（对应于推导变换）。

 

概率模型的诊断

1、利用当前推断的参数（得到的模型）生存新的观测数据，比较新数据与旧数据的相似性。

2、贝叶斯p值。

3、分离图（separation plots）。

 

更多案例

其他典型案例见 Bayesian Methods for Hackers: Probabilistic Programming and Bayesian Inference

如：用户短信行为变化、学生作弊、挑战者号事故、无监督聚类等等。

用户短信行为和无监督聚类的例子，本质上是类似的。前者在数据上有两个参数不同的Poisson分布（lambda不同），后者在数据上有两个参数不同的正态分布（均值和方差不同）。都可以采用共同的随机变量，推断不同的参数。注意构建共同变量时采用的技巧。

学生作弊问题采用了两种贝叶斯推断模型，能对比两种思路可知，灵活的数学推导思路直接影响了贝叶斯建模。理解背后的数学规律、观察数据如何产生，这些都很重要。

挑战者号事故，本质上是在拟合Logistic回归，可与“贝叶斯线性回归”案例对比。

 

贝叶斯推断不仅可以解决频率学派能解决的统计学问题，贝叶斯还能解决一些频率学派不太好解决的情景。之后有时间将对贝叶斯的优势进行简单举例和总结。本文的案例都比较简单，对于复杂的问题，需要挑选合适的先验分布，这其实并不简单；如何为不同参数选择合适的MCMC具体算法（如 M-H、NUTS、HMC等）也不简单。

 

参考资料

Bayesian Methods for Hackers: Probabilistic Programming and Bayesian Inference

贝叶斯方法：概率编程与贝叶斯推断

PyMC3 - 简介和入门

Getting started with PyMC3