scala机器学习实战(三) 保险数据预测分析(LR算法详解)
LR算法详解
前言
前景提要,前两篇文章,借助于Scala Machine Learning Projects一书,利用保险服务的数据,进行了保险行业数据的预测分析,第一篇文章分别用了三种不同的算法进行相同数据的测试,来对比三种算法的模型性能;第二篇则详细通过LR实例解释了spark机器学习中各种输入参数和模型评估的输出参数所代表的的实际意义,本篇文章将详细阐述LR算法的原理,作用以及代码实现。
文章一:scala机器学习实战(一) 保险数据预测分析
文章二:scala机器学习实战(二) 保险数据预测分析(代码参数详解)
内容概要
本篇文章将主要着力于LR算法的原理和实现两部分,希望能够以比较非学术性的词汇,来表达清楚LR算法所想要的表达含义,同时,也将通过代码实现LR算法,更加深入的理解LR算法的实现过程。
LR产生背景
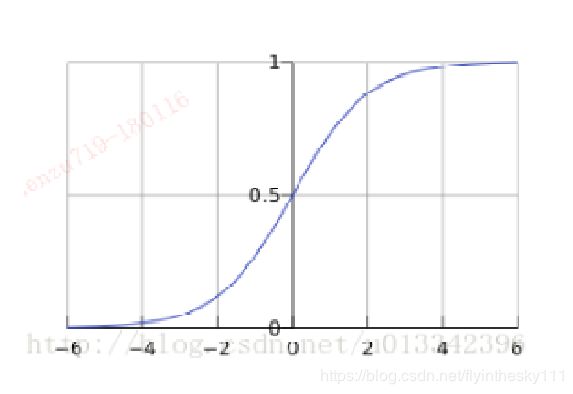
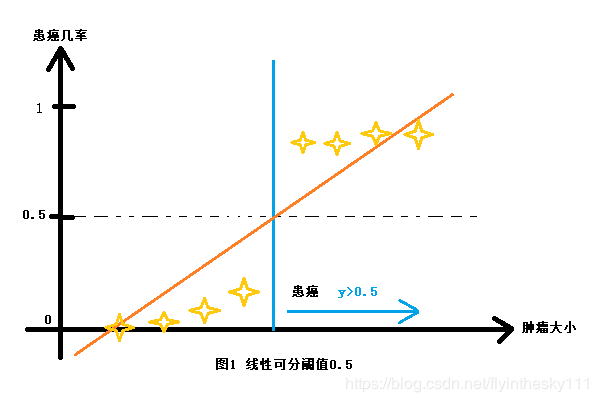
先看一下下面两张图,X表示肿瘤大小,Y轴>0.5表示是癌症,否则不是,蓝色直线表示预测直线,从图1中可以看出,X对应到预测直线上的值之后,上面4点是癌症,下面4点不是癌症。再看图二,当点排列发生变化时,0.5的阈值就很可能不适用,这主要是在线性拟合中,Y值无限延伸造成的
为了解决Y值无限延伸的问题,LR算法应运而生,把Y值限定在0和1之间,就解决了这个问题,如图三所示。
LR算法应用场景
LR算法主要解决分类问题的判别概率问题。例如垃圾邮件的判别,推荐系统,疾病预测等等。一般用来判决某件事属于某个分类的概率来确定类别。例如:一封邮件是垃圾邮件的概率是90%,就可以判定是垃圾邮件;某个用户可能概率最大的三类产品是华为,小米,OPPO,则给这个用户推荐的产品就是对应的品牌产品。类似于如此的都可以根据特征概率,来判定属于某个分类。
LR算法计算公式以及推导
计算公式
线性回归: z = θ 0 + θ 1 x 1 + θ 2 x 2 + θ 3 x 3 + . . . + θ n x n = θ T x z=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_3+...+\theta_nx_n=\theta^Tx z=θ0+θ1x1+θ2x2+θ3x3+...+θnxn=θTx
逻辑回归:
h θ ( x ) = 1 1 + e − z = 1 1 + e − θ T x h_\theta(x)=\frac{1}{1+e^{-z}}=\frac{1}{1+e^{-\theta^Tx}} hθ(x)=1+e−z1=1+e−θTx1
推导过程
其中,
y = 1 1 + e − x y=\frac{1}{1+e^{-x}} y=1+e−x1 被称作 s i g m o i d sigmoid sigmoid函数,我们可以看到,LR算法是将线性函数的结果映射到了 s i g m o i d sigmoid sigmoid函数中
s i g m o i d sigmoid sigmoid函数图形如下:
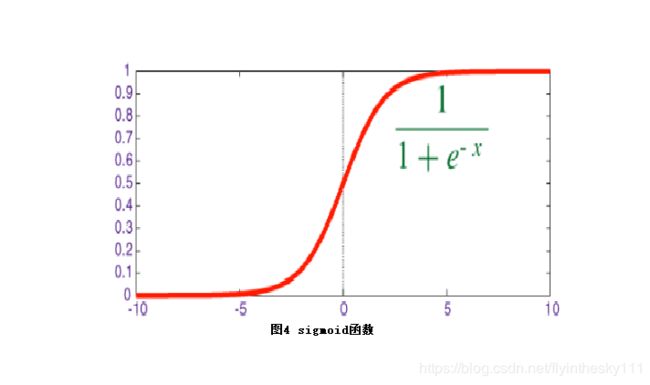
s i g m o i d sigmoid sigmoid函数的输出是在(0,1)之间,中间值是0.5,之前的公式 h θ ( x ) h_\theta(x) hθ(x)的含义就很好理解了。
h θ ( x ) h_\theta(x) hθ(x)函数输出在(0,1)之间,也就表示了数据属于某一类别的概率,例如当 h θ ( x ) h_\theta(x) hθ(x)<0.5时,数据属于A类; h θ ( x ) h_\theta(x) hθ(x)>0.5时,数据属于B类。
h θ ( x ) h_\theta(x) hθ(x)作为一个构造预测函数,他的值有特殊意义,他表示结果取一的概率,因此对于输入X分类结果为类别A和类别B 的概率分别为:
P ( y = 1 ∣ x ; θ ) = h θ ( x ) P(y=1|x;\theta)=h_\theta(x) P(y=1∣x;θ)=hθ(x)
P ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) P(y=0|x;\theta)=1-h_\theta(x) P(y=0∣x;θ)=1−hθ(x) (1)
衡量 h θ ( x ) h_\theta(x) hθ(x)函数预测好坏的 C o s t Cost Cost函数和 J ( θ ) J(\theta) J(θ)函数:
C o s t ( h θ ( x ) , y ) = { − l o g ( h θ ( x ) ) if y = 1 − l o g ( 1 − h θ ( x ) ) if y = 0 Cost(h_\theta(x),y)= \begin{cases} -log(h_\theta(x))& \text{if y = 1}\\ -log(1-h_\theta(x))& \text{if y = 0} \end{cases} Cost(hθ(x),y)={−log(hθ(x))−log(1−hθ(x))if y = 1if y = 0 (2)
J ( θ ) = 1 m ∑ i = 1 m C o s t ( h θ ( x ( i ) , y i ) ) = − 1 m [ ∑ i = 1 m y ( i ) l o g h θ ( x i ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] J(\theta)=\frac{1}{m}\sum_{i=1}^mCost(h_\theta(x^{(i)},y^{i}))=-\frac{1}{m}[\sum_{i=1}^my^{(i)}logh_\theta(x^{i})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] J(θ)=m1∑i=1mCost(hθ(x(i),yi))=−m1[∑i=1my(i)loghθ(xi)+(1−y(i))log(1−hθ(x(i)))] (3)
将(1)式综合可得:
P ( y ∣ x ; θ ) = ( h θ ( x ) ) y ( 1 − h θ ( x ) ) 1 − y P(y|x;\theta)=(h_\theta(x))^y(1-h_\theta(x))^{1-y} P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y (4)
对其取似然函数:
L ( θ ) = ∏ i = 1 m P ( y ( i ) ∣ x ( i ) ; θ ) = ∏ i = 1 m ( h θ ( x ( i ) ) y ( i ) ( 1 − h θ ( x ( i ) ) ) 1 − y ( i ) ) L(\theta)=\prod_{i=1}^mP(y^{(i)}|x{(i)};\theta)=\prod_{i=1}^m(h_\theta(x^{(i)})^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-y^{(i)}}) L(θ)=∏i=1mP(y(i)∣x(i);θ)=∏i=1m(hθ(x(i))y(i)(1−hθ(x(i)))1−y(i)) (5)
对数似然函数:
l ( θ ) = l o g L ( θ ) = ∑ i = 1 m ( y ( i ) l o g h θ ( x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ) l(\theta)=logL(\theta)=\sum_{i=1}^{m}(y^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))) l(θ)=logL(θ)=∑i=1m(y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))) (6)
求 J ( θ ) J(\theta) J(θ)的最小值:(运用的是梯度下降法)
θ j : = θ j − α 1 m s u m i = 1 m ( h θ ( x i ) − y i ) x i j \theta_j:=\theta_j-\alpha\frac{1}{m}sum_{i=1}^m(h_\theta(x_i)-y_i)x^j_i θj:=θj−αm1sumi=1m(hθ(xi)−yi)xij
算法代码实现
代码:
object LogisticRegression {
def loadDataSet() = {
//数据矩阵
val dataMat = new ArrayBuffer[Array[Double]]
//标签矩阵
val labelMat = new ArrayBuffer[Double]
//读取数据源
val data: BufferedSource = Source.fromFile("")
for (line <- data.getLines()) {
val lineArr = line.trim().split("\t").map(_.toDouble)
dataMat.append(Array(1.0, lineArr(0), lineArr(1)))
//标签矩阵
labelMat.append(lineArr(2))
}
(dataMat.toArray, labelMat.toArray)
}
//定义sigmoid函数
def sigmoid(inX: Double) = {
1.0 / (1 + math.exp(-inX))
}
def stocGradAscent(dataMatrix: Array[Array[Double]], classLabels: Array[Double], numIter: Int = 150) = {
//训练数据的长度,有多少条数据
val m = dataMatrix.length
//数据维度,每条数据的属性
val n = dataMatrix(0).length
//初始权重
var weights = Array.fill(n)(1.0)
for (j <- 1 to numIter) {
val dataIndex: ArrayBuffer[Int] = ArrayBuffer.empty
//添加索引数字
for (loc <- 0 to m - 1) dataIndex.append(loc)
for (i <- 0 to m - 1) {
val alpha = 4 / (1.0 + j + i) + 0.0001
val randIndex = Random.nextInt(dataIndex.length)
val rowZipWeight = dataMatrix(dataIndex(randIndex)).zip((weights))
val h = sigmoid(rowZipWeight.map(x => x._1 * x._2).sum)
//计算预测误差
val error = classLabels(randIndex) - h
//更新权重
weights = rowZipWeight.map(x => x._1 + alpha * error * x._2)
//移除此次计算的随机数组,下次计算重新生成
dataIndex.remove(randIndex)
}
}
weights
}
def classifyVector(inX:Array[Double],weights:Array[Double])={
//根据sigmoid函数计算的值,来判断属于哪一类
val prob = sigmoid(inX.zip(weights).map(x=> x._1* x._2).sum)
if (prob > 0.5) 1.0 else 0.0
}
def main(args: Array[String]): Unit = {
//加载数据
val dataSet = loadDataSet()
//数据矩阵
val dataMatrix = dataSet._1
//标签矩阵
val classLabels = dataSet._2
val weights = stocGradAscent(dataMatrix,classLabels,100)
//分类结果
val res = dataMatrix.map(x=> classifyVector(x,weights))
//计算准确率
val erroe: Double = res.zip(classLabels).filter(x=> x._1 == x._2).length.toDouble/classLabels.length
}
}
结语
对于LR算法的解释就到这里,我们最后的代码实现了一个简易的LR算法,后续还会推出其他两种算法的解释和简易代码实现,尽请关注!!!
下篇文章内容概要
下篇文章将会接着分析GBT算法的原理和代码实现,欢迎各位大佬指点
如有问题或者指导欢迎添加作者微信:ljelzl416108 ,一同交流学习大数据和机器学习的知识!!!