DCGAN 训练+代码总结
自从两年前蒙特利尔大学的Ian Goodfellow等人提出生成式对抗网络(Generative Adversarial Networks,GAN)的概念以来,GAN呈现出井喷式发展。
这篇发布在O’Reilly上的文章中,作者向初学者进行了GAN基础知识答疑,并手把手教给大家如何用GAN创建可以生成手写数字的程序。
本教程由两人完成:Jon Bruner是O’Reilly编辑组的一员,负责管理硬件、互联网、制造和电子学等方面的出版物;Adit Deshpande是加州大学洛杉矶分校计算机科学专业的大二学生。
判别网络
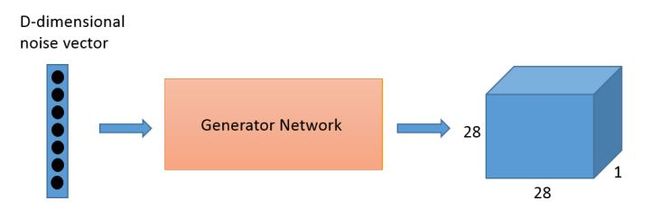
判别器就是一个典型的CNN,它能将二维或三维的像素值矩阵(matrix of pixel values)转化成一个概率。然而作为一个生成器,需要d-维度向量 d-dimensional vector ,并需要将其变为28*28的图像。ReLU和批量标准化(batch normalization)也经常用于稳定每一层的输出。
判别器的结构与TensorFlow的样例CNN分类模型密切相关。它有两层特征为5×5像素特征的卷积层,还有两个全连接层按图像中每个像素计算增加权重的层。
创建了神经网络后,通常需要将权重和偏差初始化,这项任务可以在tf.get_variable中完成。权重在截断正态分布中被初始化,偏差在0处被初始化。
tf.nn.conv2d()是TensorFlow中的标准卷积函数,它包含四个参数:首个参数就是输入图像(input volume),也就是本示例中的28×28像素的图片;第二个参数是滤波器/权矩阵,最终你也可以改变卷积的“步幅”和“填充”。这两个参数控制着输出图像的尺寸大小。
其实上面这些就是一个普通简单的二进制分类器,如果你不是初次接触CNN,应该对此并不陌生。
定义了判别器之后,我们需要回头看看生成模型。我们将以Tim O’Shea编写的简单生成器代码为基础构建模型的整体结构。
其实你可以把生成器想象成反向卷积神经网络的一种。判别器就是一个典型的CNN,它能将二维或三维的像素值矩阵(matrix of pixel values)转化成一个概率。然而作为一个生成器,需要d-维度向量 d-dimensional vector ,并需要将其变为28*28的图像。ReLU和批量标准化(batch normalization)也经常用于稳定每一层的输出。
在这个神经网络中,我们用了三个卷积层和插值,直到形成28*28像素的图像。
我们在输出层添加了一个tf.sigmoid() 激活函数,它将挤压灰色呈现白色或黑色相,从而产生一个更清晰的图像。
看起来像噪音对吧。现在我们需要训练生成网络中的权重和偏差,将随机数转变为可识别的数字。我们再看看损失函数和优化。
训练GAN
构建和调试GAN就复杂在它有两个损失函数:一个鼓励生成器创造出更好的图像,另一个鼓励判别器区分哪个是真图像,哪个是生成器生成的。
我们同时训练生成器和判别器,当判别器能够很好区分图像来自哪里时,生成器也能更好地调整它的权重和偏差来生成更以假乱真的图像。
所以,让我们首先考虑一下我们需要在网络中得到什么。判别器的目标是正确地将MNIST图像标记为真,而判别器生成的标记为假。我们将计算判别器的两种损失:Dx和1(代表MNIST中的真实图像)的损失,以及Dg与0(代表生成图像)的损失。我们将这个函数在TensorFlow中的tf.nn.sigmoid_cross_entropy_with_logits()函数上运行,计算Dx和0与Dg和1之间的交叉熵损失。下一步,你需要制定两个优化器,我们一般选择Adam优化算法,它利用了自适应学习速率和动量。我们调用Adam最小函数并且指定我们想更新的变量——也就是我们训练生成器时的生成器权重和偏差,和我们训练判别器时的判别器权重和偏差。
我们为判别器设置了两套不同的训练方案:一种是用真实图像训练判别器,另一种是用生成的“假图像”训练它。有时使用不同的学习速率很有必要,或者单独使用它们来规范学习的其他方面。
收敛GAN是一件棘手的事情,经常需要训练很长时间。可以用TensorBoard追踪训练过程:它可以用图表描绘标量属性(如损失),展示训练中的样本图像,并展示神经网络中的拓扑结构。
现在先给判别器几个简单的原始训练进行迭代,这种方法有助于形成对生成器有用的梯度。
之后我们继续进行主要的训练循环。当训练生成器的时候,我们需要将随机的z向量输入到生成器中,并将其输出传递给判别器(这就是我们早先定义的Dg变量)。生成器的权重和偏差将被改变,主要是为了生成能骗过判别器的图像。
为了训练判别器,我们将给它提供一组来自MNIST数据集中的正面例子,并且再次用生成的图像训练判别器,用它们作为反面例子。
因为训练GAN通常需要很长时间,所以我们建议如果您是第一次使用这个教程,建议先不要运行这个代码块。但你可以先执行下面的代码块,让它生成出一个预先训练模型。
如果你想自己运行这个代码块,请做好长时间等待的准备:在速度相对较快的GPU上运行大概需要3小时,在台式机的CPU上可能耗费10倍时间。
所以,建议你跳过上面直接执行下面的cell。它加载了一个我们在高速GPU机器上训练了10小时的模型,你可以试验下训练过的GAN。
训练不易
众所周知训练GAN很艰难。在没有正确的超参数、网络体系结构和培训流程的情况下,判别器会压制生成器。
一个常见的故障模式是,判别器压制了生成器,肯定地把生成图像定义为假的。当判别器以绝对肯定时,会使生成器无梯度可降。这就是为什么我们建立判别器来产生未缩放的输出,而不是通过一个sigmoid函数将其输出推到0或1。
在另一种常见的故障模式(模式崩溃)中,生成器发现并利用了判别器中的一些弱点,如果它不顾生成器输入z.变量,生成了很多相似图像,你是可以识别出这种模式崩溃的。模式崩溃有时可以通过“强化”鉴别器来修正,例如通过调整其训练速率或重新配置它的层。
先看main.py:
with tf.Session(config=run_config) as sess:
if FLAGS.dataset == 'mnist':
dcgan = DCGAN(
sess,
input_width=FLAGS.input_width,
input_height=FLAGS.input_height,
output_width=FLAGS.output_width,
output_height=FLAGS.output_height,
batch_size=FLAGS.batch_size,
y_dim=10,
c_dim=1,
dataset_name=FLAGS.dataset,
input_fname_pattern=FLAGS.input_fname_pattern,
is_crop=FLAGS.is_crop,
checkpoint_dir=FLAGS.checkpoint_dir,
sample_dir=FLAGS.sample_dir)
再看model.py:
def discriminator(self, image, y=None, reuse=False):
with tf.variable_scope("discriminator") as scope:
if reuse:
scope.reuse_variables()
yb = tf.reshape(y, [self.batch_size, 1, 1, self.y_dim])
x = conv_cond_concat(image, yb)
h0 = lrelu(conv2d(x, self.c_dim + self.y_dim, name='d_h0_conv'))
h0 = conv_cond_concat(h0, yb)
h1 = lrelu(self.d_bn1(conv2d(h0, self.df_dim + self.y_dim, name='d_h1_conv')))
h1 = tf.reshape(h1, [self.batch_size, -1])
h1 = tf.concat_v2([h1, y], 1)
h2 = lrelu(self.d_bn2(linear(h1, self.dfc_dim, 'd_h2_lin')))
h2 = tf.concat_v2([h2, y], 1)
h3 = linear(h2, 1, 'd_h3_lin')
return tf.nn.sigmoid(h3), h3def conv2d(input_, output_dim,
k_h=5, k_w=5, d_h=2, d_w=2, stddev=0.02,
name="conv2d"):
with tf.variable_scope(name):
w = tf.get_variable('w', [k_h, k_w, input_.get_shape()[-1], output_dim],
initializer=tf.truncated_normal_initializer(stddev=stddev))
conv = tf.nn.conv2d(input_, w, strides=[1, d_h, d_w, 1], padding='SAME')
biases = tf.get_variable('biases', [output_dim], initializer=tf.constant_initializer(0.0))
conv = tf.reshape(tf.nn.bias_add(conv, biases), conv.get_shape())
return convdef generator(self, z, y=None):
with tf.variable_scope("generator") as scope:
s_h, s_w = self.output_height, self.output_width
s_h2, s_h4 = int(s_h/2), int(s_h/4)
s_w2, s_w4 = int(s_w/2), int(s_w/4)
# yb = tf.expand_dims(tf.expand_dims(y, 1),2)
yb = tf.reshape(y, [self.batch_size, 1, 1, self.y_dim])
z = tf.concat_v2([z, y], 1)
h0 = tf.nn.relu(
self.g_bn0(linear(z, self.gfc_dim, 'g_h0_lin')))
h0 = tf.concat_v2([h0, y], 1)
h1 = tf.nn.relu(self.g_bn1(
linear(h0, self.gf_dim*2*s_h4*s_w4, 'g_h1_lin')))
h1 = tf.reshape(h1, [self.batch_size, s_h4, s_w4, self.gf_dim * 2])
h1 = conv_cond_concat(h1, yb)
h2 = tf.nn.relu(self.g_bn2(deconv2d(h1,
[self.batch_size, s_h2, s_w2, self.gf_dim * 2], name='g_h2')))
h2 = conv_cond_concat(h2, yb)
return tf.nn.sigmoid(
deconv2d(h2, [self.batch_size, s_h, s_w, self.c_dim], name='g_h3'))生成器以及判别器的输出:
self.G = self.generator(self.z, self.y)
self.D, self.D_logits = \
self.discriminator(inputs, self.y, reuse=False)
self.D_, self.D_logits_ = \
self.discriminator(self.G, self.y, reuse=True)再看损失函数:
self.d_loss_real = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(
logits=self.D_logits, targets=tf.ones_like(self.D)))
self.d_loss_fake = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(
logits=self.D_logits_, targets=tf.zeros_like(self.D_)))
self.g_loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(
logits=self.D_logits_, targets=tf.ones_like(self.D_)))优化器:
d_optim = tf.train.AdamOptimizer(config.learning_rate, beta1=config.beta1) \
.minimize(self.d_loss, var_list=self.d_vars)
g_optim = tf.train.AdamOptimizer(config.learning_rate, beta1=config.beta1) \
.minimize(self.g_loss, var_list=self.g_vars)for epoch in xrange(config.epoch):
batch_idxs = min(len(data_X), config.train_size) // config.batch_size
for idx in xrange(0, batch_idxs):
batch_images = data_X[idx*config.batch_size:(idx+1)*config.batch_size]
batch_labels = data_y[idx*config.batch_size:(idx+1)*config.batch_size]
batch_images = np.array(batch).astype(np.float32)[:, :, :, None]
batch_z = np.random.uniform(-1, 1, [config.batch_size, self.z_dim]) \
.astype(np.float32)
# Update D network
_, summary_str = self.sess.run([d_optim, self.d_sum],
feed_dict={
self.inputs: batch_images,
self.z: batch_z,
self.y:batch_labels,
})
self.writer.add_summary(summary_str, counter)
# Update G network
_, summary_str = self.sess.run([g_optim, self.g_sum],
feed_dict={
self.z: batch_z,
self.y:batch_labels,
})
self.writer.add_summary(summary_str, counter)
# Run g_optim twice to make sure that d_loss does not go to zero (different from paper)
_, summary_str = self.sess.run([g_optim, self.g_sum],
feed_dict={ self.z: batch_z, self.y:batch_labels })
self.writer.add_summary(summary_str, counter)
errD_fake = self.d_loss_fake.eval({
self.z: batch_z,
self.y:batch_labels
})
errD_real = self.d_loss_real.eval({
self.inputs: batch_images,
self.y:batch_labels
})
errG = self.g_loss.eval({
self.z: batch_z,
self.y: batch_labels
})
counter += 1How to Train a GAN? Tips and tricks to make GANs work
1. Normalize the inputs
- normalize the images between -1 and 1
- Tanh as the last layer of the generator output
2: A modified loss function
In GAN papers, the loss function to optimize G is min (log 1-D), but in practice folks practically use max log D
- because the first formulation has vanishing gradients early on
- Goodfellow et. al (2014)
In practice, works well:
- Flip labels when training generator: real = fake, fake = real
3: Use a spherical Z
- Dont sample from a Uniform distribution
![]()
- Sample from a gaussian distribution
![]()
- When doing interpolations, do the interpolation via a great circle, rather than a straight line from point A to point B
- Tom White's Sampling Generative Networks ref code https://github.com/dribnet/plat has more details
4: BatchNorm
- Construct different mini-batches for real and fake, i.e. each mini-batch needs to contain only all real images or all generated images.
- when batchnorm is not an option use instance normalization (for each sample, subtract mean and divide by standard deviation).
![]()
5: Avoid Sparse Gradients: ReLU, MaxPool
- the stability of the GAN game suffers if you have sparse gradients
- LeakyReLU = good (in both G and D)
- For Downsampling, use: Average Pooling, Conv2d + stride
- For Upsampling, use: PixelShuffle, ConvTranspose2d + stride
- PixelShuffle: https://arxiv.org/abs/1609.05158
6: Use Soft and Noisy Labels
- Label Smoothing, i.e. if you have two target labels: Real=1 and Fake=0, then for each incoming sample, if it is real, then replace the label with a random number between 0.7 and 1.2, and if it is a fake sample, replace it with 0.0 and 0.3 (for example).
- Salimans et. al. 2016
- make the labels the noisy for the discriminator: occasionally flip the labels when training the discriminator
7: DCGAN / Hybrid Models
- Use DCGAN when you can. It works!
- if you cant use DCGANs and no model is stable, use a hybrid model : KL + GAN or VAE + GAN
8: Use stability tricks from RL
- Experience Replay
- Keep a replay buffer of past generations and occassionally show them
- Keep checkpoints from the past of G and D and occassionaly swap them out for a few iterations
- All stability tricks that work for deep deterministic policy gradients
- See Pfau & Vinyals (2016)
9: Use the ADAM Optimizer
- optim.Adam rules!
- See Radford et. al. 2015
- Use SGD for discriminator and ADAM for generator
10: Track failures early
- D loss goes to 0: failure mode
- check norms of gradients: if they are over 100 things are screwing up
- when things are working, D loss has low variance and goes down over time vs having huge variance and spiking
- if loss of generator steadily decreases, then it's fooling D with garbage (says martin)
11: Dont balance loss via statistics (unless you have a good reason to)
- Dont try to find a (number of G / number of D) schedule to uncollapse training
- It's hard and we've all tried it.
- If you do try it, have a principled approach to it, rather than intuition
For example
while lossD > A:
train D
while lossG > B:
train G
12: If you have labels, use them
- if you have labels available, training the discriminator to also classify the samples: auxillary GANs
13: Add noise to inputs, decay over time
- Add some artificial noise to inputs to D (Arjovsky et. al., Huszar, 2016)
- http://www.inference.vc/instance-noise-a-trick-for-stabilising-gan-training/
- https://openreview.net/forum?id=Hk4_qw5xe
- adding gaussian noise to every layer of generator (Zhao et. al. EBGAN)
- Improved GANs: OpenAI code also has it (commented out)
14: [notsure] Train discriminator more (sometimes)
- especially when you have noise
- hard to find a schedule of number of D iterations vs G iterations
15: [notsure] Batch Discrimination
- Mixed results
16: Discrete variables in Conditional GANs
- Use an Embedding layer
- Add as additional channels to images
- Keep embedding dimensionality low and upsample to match image channel size
17: Use Dropouts in G in both train and test phase
- Provide noise in the form of dropout (50%).
- Apply on several layers of our generator at both training and test time
- https://arxiv.org/pdf/1611.07004v1.pdf
reference:
https://github.com/soumith/ganhacks
https://zhuanlan.zhihu.com/p/27440393