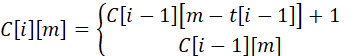找零钱问题【动态规划】【python】

问题描述

设有n种不同面值的硬币，各硬币的面值存于数组T[1:n]中。现要用这些面值的硬币来找钱，可以实用的各种面值的硬币个数不限。当只用硬币面值T[1],T[2],…,T[i]时，可找出钱数j的最少硬币个数记为C(i,j)。若只用这些硬币面值，找不出钱数j时，记C(i,j)=∞。

« 编程任务

设计一个动态规划算法，对1≤j≤L，计算出所有的C( n,j )。算法中只允许实用一个长度为L的数组。用L和n作为变量来表示算法的计算时间复杂性

« 数据输入

从屏幕输入数据。输入第1行中有1个正整数n（n<=13），表示有n种硬币可选。接下来的一行是每种硬币的面值。由用户输入待找钱数j。

« 结果输出

 程序运行结束时，将计算出的所需最少硬币个数输出到屏幕。

输入示例	输出文件示例
3 1 2 5 9	3

建立二维动态规划表

m为该次需要找的钱数，

i为所用钱的种类数，

边界条件：

1）当找不开时，C[i][m]=∞

2）当m=0时，C[i][m]=0

递归关系：

但是要注意找不开的情况，

只有m>=t[i-1]时，才会走：

m

编程检验的时候可以使用

3

2 3 5

6

这个例子

def give_coins(t,amount):
    maxc=(float('inf'))
    lent=len(t)
    C=[[maxc for i in range(amount+1)] for k in range(lent+1)]
    for i in range(lent+1):
        for m in range(amount+1):
            if i==0:  #初始化第一行
                C[i][m]=maxc
            elif m==0:  #初始化第一列
                C[i][m]=0
            else:
                if m-t[i-1]>=0:  
                    C[i][m]=min(C[i][m-t[i-1]]+1,C[i-1][m])

                else:
                    C[i][m]=C[i-1][m]
    return C

#回溯（未成功）
# def back(t,c):
#     select=[]
#     lent=len(t)
#     import numpy as np
#     minc=(np.min(C,axis=0))[-1]   #数组C最后一列的最小值
#     minarg=(np.argmin(C,axis=0))[-1]   #数组C最后一列最小值的下标
#     while minc>0:
#         minc-=t[lent-1]
#         minarg-=t[lent-1]


if __name__=="__main__":

    n=(int)(input())
    #小菜鸟刚学会把n个数输入到列表中
    lista=[int(i) for i in input().split()]
    # print(lista)
    amount=(int)(input())
    result=give_coins(lista,amount)
    #动态规划表
    # for list in result:
    #     print(list)
    import numpy as np
    minc=(np.min(result,axis=0))[-1]   #数组C最后一列的最小值
    print(int(minc))