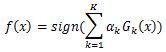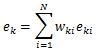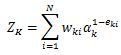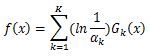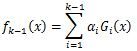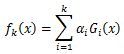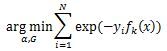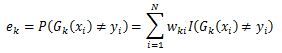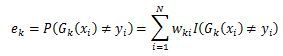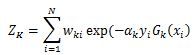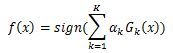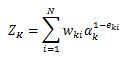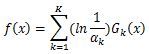机器学习之集成学习(二)AdaBoost算法
一、boosting算法的基本原理
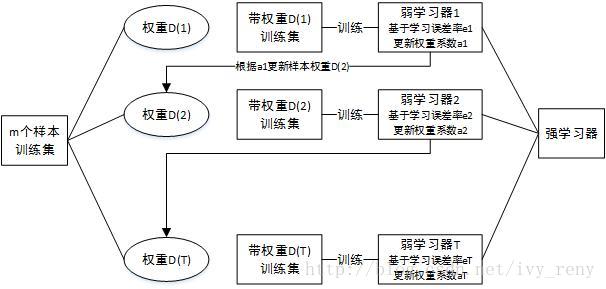
集成学习器根据个体学习器的生成是否存在依赖关系,可以分为两类:个体学习器间存在强依赖关系,必须串行生成,代表算法是boosting系列算法;个体学习器之间不存在强依赖关系,可以并行生成,代表算法是bagging和随机森林系列算法。在boosting系列算法中,AdaBoost是最著名的算法之一。AdaBoost既可以用作分类,也可以用作回归。Boosting算法的工作机制是首先从训练集中用初始权重训练出一个弱学习器1,根据弱学习器的学习误差率来更新训练样本的权重,使弱学习器1学习误差率高的训练样本点的权重变高,在后面的弱学习器2中得到更多的重视,然后基于调整权重后的训练集来训练弱学习器2,如此重复,直到弱学习器数目达到事先指定的数目T,最后将T个弱学习器通过集合策略进行整合,得到最终的强学习器。从偏差-方差分解的角度看,Boosting主要关注降低偏差,因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成。
Boosting系列算法需要解决以下几个具体问题:
1、如何计算学习误差e?
2、如何得到弱学习器权重系数a?
3、如何更新样本权重D?
4、使用何种结合策略?
二、AdaBoost算法的基本思路
假设训练数据集2.1 Adaboost的分类问题
误差率e
由于多元分类是二元分类的推广,这里假设是二元分类,输出为{-1, 1},则第k个弱分类器Gk(x)在训练集上的加权误差率为弱学习器权重系数a
对于二元分类问题,第k个弱分类器Gk(x)的权重系数为从上式可以看出,分类误差率e_k越大,则对应的弱分类器权重系数越小,误差率小的弱分类器权重系数越大。这个权重系数公式的来源在后文AdaBoost损失函数优化时再讲。
更新样本权重D
假设第k个弱分类器的样本集权重系数为这里Z_K是规范化因子
从
结合策略
AdaBoost分类采用加权平均法,最终的强分类器为2.2 Adaboost的回归问题
AdaBoost的回归问题有很多变种,这里以AdaBoost R2算法为准误差率e
第k个弱学习器在训练集上的最大误差这里的误差损失为线性。如果用平方误差
如果用指数误差
最终得到第k个弱学习器的误差率
弱学习器权重系数a
更新样本权重D
第k+1个弱学习器的样本集权重系数为这里Z_K是规范化因子
结合策略
采用加权平均法,最终的强回归器为三、AdaBoost分类问题的损失函数优化
AdaBoost的弱学习器权重系数公式和样本权重更新公式,可以从AdaBoost的损失函数推导出来。AdaBoost算法是模型为加法模型、损失函数为指数函数、学习算法为前向分步算法时的二类分类学习方法。
模型为加法模型很好理解,最终的强分类器是若干个弱分类器加权平均得到的。
前向分步学习算法也好理解,算法是通过一轮轮的弱学习器学习,利用前一个弱学习器的结果来更新后一个弱学习器的训练集权重,即第k-1轮的强学习器为
第k轮的强学习器为
可以得到
AdaBoost损失函数为指数函数,定义损失函数为
利用前向分步学习算法的关系可以得到
令
首先求
将
其中e_k为分类误差率。
最后求样本权重的更新,利用
四、AdaBoost二元分类问题算法流程
输入:样本集输出:最终的强分类器f(x)
(1) 初始化样本集权重为
(2) 对于k=1, 2, …, K
a) 使用权重D(k)的样本集来训练数据,得到弱分类器
b) 计算
c) 计算弱分类器的权重系数
d) 更新样本集的权重分布
这里Z_K是规范化因子
(3) 构建最终分类器
对于AdaBoost多元分类算法,其原理和二元分类类似,最主要区别在弱分类器的系数上。
其中R为类别数,如果是二元分类,R=2,则上式和二元分类算法中的弱分类器系数一致。
五、AdaBoost回归问题算法流程
AdaBoost回归算法变种很多,这里以AdaBoost R2回归算法为例。输入:样本集
输出:最终的强学习器f(x)
(1) 初始化样本集权重为
(2) 对于k=1, 2, …, K
a) 使用权重D(k)的样本集来训练数据,得到弱分类器
b) 计算训练集上的最大误差
如果是线性误差,则
如果是平方误差,则
如果是指数误差,则
d) 计算回归误差率
e) 计算弱学习器的权重系数
f) 更新样本集的权重分布
这里Z_K是规范化因子
(3) 构建最终强学习器
六、AdaBoost算法的正则化
为防止AdaBoost过拟合,通常会加入正则化项,这个正则化项通常称为步长,定义为ν,对于前面弱学习器的迭代七、AdaBoost小结
理论上任何学习器都可以用于Adaboost,但一般来说,使用最广泛的Adaboost弱学习器是决策树和神经网络。对于决策树,Adaboost分类用了CART分类树,而Adaboost回归用了CART回归树。Adaboost的主要优点有:
(1)Adaboost作为分类器时,分类精度很高;
(2)在Adaboost的框架下,可以使用各种回归分类模型来构建弱学习器,非常灵活;
(3)作为简单的二元分类器时,构造简单,结果可理解;
(4)不容易发生过拟合。
Adaboost的主要缺点有:
对异常样本敏感,异常样本在迭代中可能会获得较高的权重,影响最终的强学习器的预测准确性。