python - 用struct以及HxD查看浮点数在内存中的存储，默认是双精度浮点数

In [25]: for i in struct.pack("!d",0.0456):
    ...:     print(bin(i)[2:].rjust(8,"0"),end="")
    ...:
    ...:
0011111110100111010110001110001000011001011001010010101111010100

以上代码也可缩写为：

In [32]: print("".join(bin(i)[2:].rjust(8,"0") for i in struct.pack("!d",0.0456)))
0011111110100111010110001110001000011001011001010010101111010100

之所以用d双精度，是因为我实在是无法在内存中找到f单精度，于是赋值了多个变量，观察内存状态，之后确定就是他了

In [1]: a=0.0456

In [2]: hex(id(a))
Out[2]: '0x20f7d6d6d30'

In [3]: a.__sizeof__()
Out[3]: 24

In [4]: import struct

In [8]: "".join(hex(i)[2:].rjust(2,"0")+" " for i in struct.pack("@d",a))
Out[8]: 'd4 2b 65 19 e2 58 a7 3f '

python下，浮点存储的结构：头 类型 数据

参考：
Python中struct.pack()和struct.unpack()用法详细说明

In [22]: "".join(bin(i)[2:].rjust(8,"0")+" " for i in struct.pack("!d",1))
Out[22]: '00111111 11110000 00000000 00000000 00000000 00000000 00000000 00000000 '

In [23]: "".join(bin(i)[2:].rjust(8,"0")+" " for i in struct.pack("!d",2))
Out[23]: '01000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 '

In [24]: "".join(bin(i)[2:].rjust(8,"0")+" " for i in struct.pack("!d",3))
Out[24]: '01000000 00001000 00000000 00000000 00000000 00000000 00000000 00000000 '

1、2、3在浮点中很奇妙，其实1就可以验证浮点存储的S E M位，如果不确定，2，3，出来后就很确定了。
于是双精度d的存储方式就是

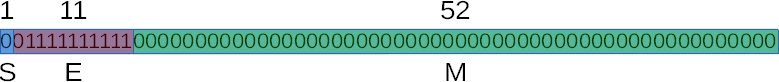
最大数：0 11111111110 11111111111111111111111111111111111111111111111111111111111111111111

In [27]: struct.unpack("!d",b'\x7f\xef\xff\xff\xff\xff\xff\xff')
Out[27]: (1.7976931348623157e+308,)

In [45]: 2**1023*1.999999999999999
Out[45]: 1.797693134862315e+308

In [46]: 2**1023*1.9999999999999999
Out[46]: inf

下面的无穷是进位超了，于是其实进位的原则还是很简单的，但是一旦E：11111111111，就无穷了！？