对问卷数据进行线性分析
引入包
library(dplyr)
library(ggplot2)
library(tidyr)绘制时间序列图
原始数据:
可以看到日期是字符串形式,现在将其转换为数值型
menus <- read.csv(file.choose(), stringsAsFactors = FALSE, colClasses = c('factor', 'Date', 'numeric'))再次观察:
> head(menus)
品名 日期 销售额
1 关东煮 2015-03-01 4046
2 关东煮 2015-03-02 3437
3 关东煮 2015-03-03 3191
4 关东煮 2015-03-04 3499
5 关东煮 2015-03-05 3536
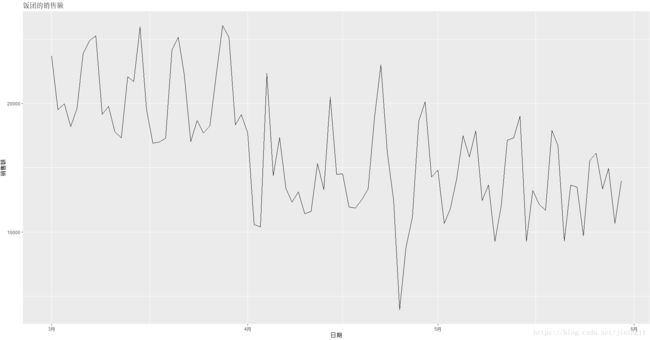
6 关东煮 2015-03-06 3841针对饭团绘制销量随时间的变化曲线
# 筛选行
fantuan <- menus %>% filter(品名 == '饭团')
# 制作饭团的时间序列图
ggplot(fantuan, aes(日期, 销售额)) + geom_line() + scale_x_date() + ggtitle('饭团的销售额')
观察多因子两两影响
接下来观察各个面条之间销量的影响,要筛选出所有的面条,我们需要更加复杂的语句
# 筛选出所有的面条
noodles <- menus %>% filter(品名 %in% c('意大利面', '乌冬面', '拉面', '什锦面'))> head(noodles)
品名 日期 销售额
1 乌冬面 2015-03-01 8849
2 乌冬面 2015-03-02 6063
3 乌冬面 2015-03-03 6060
4 乌冬面 2015-03-04 6283
5 乌冬面 2015-03-05 7138
6 乌冬面 2015-03-06 9264由于相关分析分析的变量需要单独占一列,而上述表头显然不符合要求,因而我们需要将长表转为宽表
> noodles2 <- noodles %>% spread(品名, 销售额)
> head(noodles2)
日期 拉面 什锦面 乌冬面 意大利面
1 2015-03-01 17644 6245 8849 5947
2 2015-03-02 12756 4469 6063 5010
3 2015-03-03 13764 5159 6060 5263
4 2015-03-04 14670 4399 6283 5150
5 2015-03-05 13371 4791 7138 4883
6 2015-03-06 18845 6039 9264 6410由于日期也是不相关的因子,因此我们将其去除:
> noodles2[,-1]
拉面 什锦面 乌冬面 意大利面
1 17644 6245 8849 5947
2 12756 4469 6063 5010
3 13764 5159 6060 5263
4 14670 4399 6283 5150
5 13371 4791 7138 4883
6 18845 6039 9264 6410计算相关系数并绘制散点图矩阵:
> noodles2[,-1] %>% cor
拉面 什锦面 乌冬面 意大利面
拉面 1.0000000 0.9220467 0.9129860 0.9188441
什锦面 0.9220467 1.0000000 0.9099195 0.9101794
乌冬面 0.9129860 0.9099195 1.0000000 0.8979937
意大利面 0.9188441 0.9101794 0.8979937 1.0000000
> noodles2[,-1] %>% pairs如下图所示的散点图可用来快速分析,找出可能有所关联的变量
我们可以看到相关因子有0.8,0.9,1.0等等,那我们该如何判断相关关系大还是小呢?一般来说,有这样几条规则:
| 相关系数 | 相关程度 |
|---|---|
| -1.0~-0.7 |
强负相关 |
| -0.7~-0.3 | 弱负相关 |
| -0.3~0.3 | 不相关 |
| 0.3~0.7 | 弱负相关 |
| 0.7~1.0 | 强正相关 |
对饭团和牛奶进行最小二乘拟合
milk <- menus %>% filter(品名 %in% c('饭团', '牛奶')) %>% spread(品名, 销售额)
milk %>% ggplot(aes(饭团, 牛奶)) +
geom_point(size = 2, color = 'grey50') +
geom_smooth(method = "lm", se = TRUE) +
ggtitle('饭团与牛奶的散点图')
summary(lm(饭团~牛奶, data = milk))接下来重点看一下从summary得到的总结信息
Call: # 调用了哪些函数
lm(formula = 饭团 ~ 牛奶, data = milk)
Residuals: # 残差,即实际观察值与估计值(拟合值)之间的差,下面依次是最小值/四分位点/最大值
Min 1Q Median 3Q Max
-9406.8 -2660.0 -870.2 3016.4 9643.9
Coefficients: # 系数
Estimate Std. Error t value Pr(>|t|)
# 截距估计值 误差 t值 p值(P值小于0.05,抛弃零假设即'斜率为零',采信备择假设)
(Intercept) 24125.0042 1238.8045 19.474 < 2e-16 ***
# 斜率估计值 误差 t值 p值
牛奶 -3.2530 0.4911 -6.624 2.58e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3815 on 89 degrees of freedom
判定系数,越接近1越好,越接近0越差
Multiple R-squared: 0.3302, Adjusted R-squared: 0.3227
F统计量,P值
F-statistic: 43.88 on 1 and 89 DF, p-value: 2.58e-09
相关系数和线性回归分析通常一个在前一个在后,如果确认有较高的相关系数,才能采取回归分析