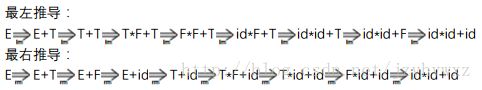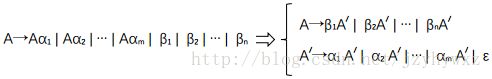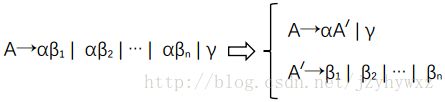【编译原理】语法分析(一)
词法分析器把源程序转换成了一个词素序列,它让我们知道了一个符号序列’i’、’f’是一个关键词”if”,而一个符号序列’1’、’2’、’3’、’4’是一个常量”1234”等等。但是,词法分析器的工作也到此为止了,它不能说明几个词素之间的关系。例如,对于词素串”int”、”x”、”=”、”1”、”;”,词法分析器不知道它是一个语句;对于词素串”int”、”x”、”==”、”1”、”;”,词法分析器不能检测出它的语法错误。为此,在词法分析之后,还需进行语法分析。
语法分析器的作用
我们都知道,在使用某一种程序设计编写程序时,都要遵循一套特定的规则。比如,在C语言中,一个程序由多个函数组成,一个函数由声明和语句组成,一个语句由表达式组成等等。这组规则精确描述了一个良构的程序设计语言的语法。语法分析器能够确定一个源程序的语法结构,能够检测出源程序中的语法错误,并且能够从常见的错误中恢复并继续处理程序的其余部分。
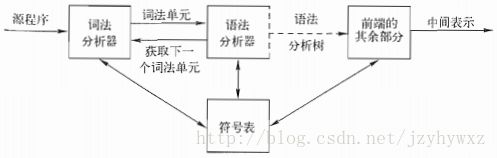
一个语法分析器从词法分析器获得一个词素序列,并验证这个序列是否可以由源语言的文法生成。语法分析器会构造一棵语法分析树,并把它传递给编译器的其他部分进一步处理,在构建语法分析树的过程中,就验证了这个词素序列是否符合源语言的文法。语法分析器在编译器中的位置如下图:
文法
一个文法用于系统的描述程序设计语言的构造的语法。一个正确设计的文法给出了一个语言的结构,该结构有助于把源程序翻译为正确的目标代码,也有助于检测错误。
上下文无关文法
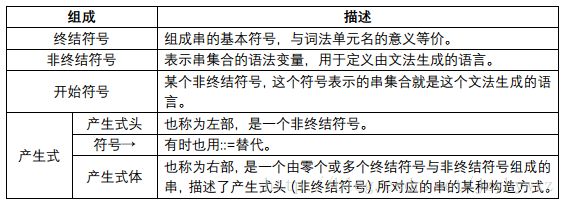
一个上下文无关文法(下文简称文法)由终结符号、非终结符号、一个开始符号和一组产生式组成:
对于产生式头相同的两个或多个产生式,可以把它们的产生式体用“|”连接写成一个产生式。例如,对产生式E→E+T和E→T,可以写成E→E+T|T。
一个贯穿全文的表达式文法
在进入主题之前,先给出一个简单的表达式文法,把它称为文法G,它将作为一个贯穿全文的例子:
E→E+T|T
T→T*F|F
F→(E)|id在文法G中,有3个产生式。其中,符号”+”、”*”、”(“、”)”、”id”是终结符号,符号”E”、”T”、”F”是非终结符号;符号E是开始符号,表示文法G可以生成的语言。
关于符号的约定
在下文中由于需要会出现大量的符号,为了减少冗余和方便理解,我们在此对使用的符号有如下约定:
- 大写字母表示非终结符号,如A、B、C等;
- 希腊字母表示任意由非终结符号和终结符号组成的串或者空串,如α、β、γ等。
推导和规约
语法分析器在构建一棵语法分析树时,常用的方法可以分为自顶向下和自底向上的。顾名思义,自顶向下的方法是从语法分析树的根结点开始向叶子结点构造的方法,自底向上的方法是从语法分析树的叶子结点开始向根结点构造的方法。在自顶向下的构造过程中,需要从一个非叶子结点“推导”出其子树;在自底向上的构造中,需要把几个非根结点“规约”成其根结点。
推导
从产生式的角度来看,一次推导过程是把产生式的左部替换成产生式的右部的过程。
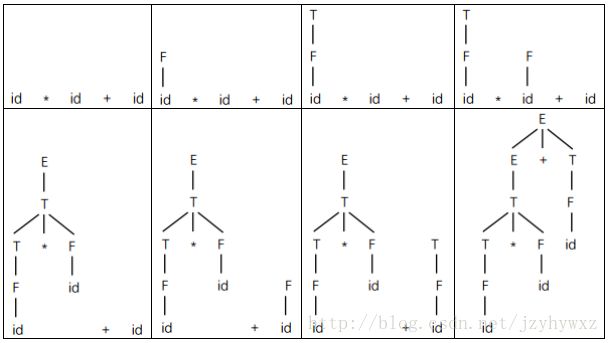
对文法G,从E到id*id+id的一个最左推导和最右推导分别为:
其中,id*id+id是文法G的一个句子,其他中间步骤是文法G的句型。从此亦可看出,对相同句型的推导过程不唯一。
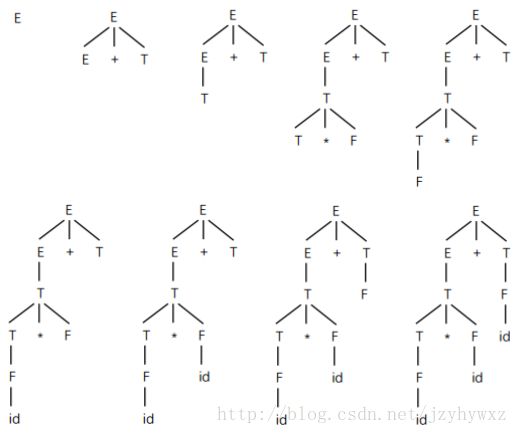
推导过程可以用语法分析树表示,从E到id*id+id的最左推导的语法分析过程如下图所示:
每棵语法分析树对应于某一次推导,从左到右把语法分析树的叶子结点连接起来就是文法G的一个句型,也称为语法分析树的结果或边缘,最后一棵语法分析树的叶子结点从左到右连接起来是文法G的一个句子。
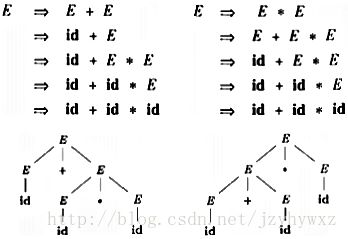
规约
规约是推导的逆过程,一次规约是把一个与某产生式体相匹配的串替换为该产生式头的非终结符号。
规约过程可以用于自底向上构造语法分析树。例如,把id*id+id规约成E,这里的每次规约是某次最右推导的逆过程,构造的语法分析树如下图所示:
设计文法
本节将介绍如何对一个文法进行转换使其更适用于语法分析,这些转换方法包括消除二义性,消除左递归和提取左公因子。
消除二义性
如果一个文法可以为某个句子生成多棵语法分析树,那么它就是二义性的,简单地说,二义性文法就是对同一个句子有多个最左推导或多个最右推导的文法。
考虑下面的文法:
E→E+E
E→E*E
E→(E)
E→id它对句子id+id*id有两个最左推导,下图给出了推导过程和相应的语法分析树:
可以看出,这两个推导过程反映了加法和乘法的优先级问题,左边的推导乘法优先级比加法高,右边的推导加法的优先级比乘法高。实际上,左边的推导过程更符合我们的观念。
通过把该文法改写成文法G的形式,可以解决这个二义性问题,该文法和文法G都生成同样的语言。
消除左递归
如果一个文法对一个非终结符号A,经过一次或多次推导后得到串Aα,那么这个文法是左递归的。如果该文法中存在形如A→Aα的产生式,则该产生式是立即左递归的。
在介绍消除文法的左递归之前,我们先介绍如何消除产生式的立即左递归。对任意立即左递归的产生式,可以用下面的方法消除立即左递归:
右边的两个产生式生成的串集合和左边的产生式生成的串集合是相同的,并且右边的两个产生式没有左递归,这样就消除了产生式的左递归。
现在正式介绍对一个左递归的文法如何消除其左递归。对一个左递归的文法,用下面的方法消除左递归:
对文法G,消除它的左递归:
- 将非终结符号排序为E、T、F;
- 当i=1时,对符号E,产生式
E→E+T|T是立即左递归的,把它替换为E→TE'和E'→+TE'|ε; - 当i=2时,对符号T,产生式
T→T*F|F中没有E,但它是立即左递归的,把它替换为T→FT'和T'→*FT'|ε; - 当i=3时,对符号F,产生式
F→(E)|id中有E,把E替换为TE'后得到F→(TE')|id,它不是立即左递归的,算法结束; - 最后得到的非左递归文法为:
E→TE'
E'→+TE'|ε
T→FT'
T'→*FT'|ε
F→(TE')|id提取左公因子
当使用自顶向下的方法构造语法分析树时,如果在“展开”一个非终结符号的结点时,有不止一个产生式可以选择,此时无法明确知道该使用哪一个产生式。为了解决这个问题,我们可以通过改写产生式来推后这个决定,等获得足够的信息后再做出正确的选择。
例如,对于产生式A→+α|+β,假设α和β开头的符号不同,当看到输入“+”时,不能明确决定使用+α还是+β来替换A,只有继续读入下一个输入,才能确定到底使用哪一个产生式。对此,可以把A→+α|+β转换成A→+A'和A'→α|β,这样当看到输入“+”时,可以把A替换为A',再根据后续的输入决定如何替换A'。
对一个文法提取左公因子,对于每个非终结符号A,找出它的两个或多个选项之间的最长公共前缀α,如果α不是空串,那么将所有头为A的产生式做如下替换:
其中,γ表示所有不以α开头的串,A'是一个新的非终结符号。不断应用这个转换,直到每个非终结符号的任意两个产生式体都没有公共前缀为止。