翻译-Forecasting Sunspot Time Series Using Deep Learning Methods

摘要

为了预测太阳周期25，我们使用了太阳黑子数（SSN）的值，这些值已经从1749年到现在定期测量。 在这项研究中，我们将SSN数据集（由1749年至2018年间的SSN组成）转换为时间序列，并借助深度学习（DL）算法进行了十年预测。 我们的结果表明，DL算法等长期短期记忆（LSTM）和神经网络自回归（NNAR）等算法的性能优于ARIMA，Naive，Seasonal Naive，Mean和Drift等许多算法。 作为大时间序列估计过程中的经典算法。 使用R编程语言，还预测太阳周期（SC）25的最大振幅将在2022和2023之间达到。

1. Introduction

太阳活动对人类，其他生物以及世界上的重要技术产生了重大影响。 由于太阳活动的变化约为11年，行星际环境和磁层中近地空间的偏差会影响这一时期的电离层等离子体密度。 此外，太阳活动的变化会影响航空导航，太空导航，太空飞行，雷达，高频无线电通信和地面电线。 这些变化还可能影响世界上的气候和生物，包括人类（Aguirre，Letellier和Maquet，2008; Pesnell，2008; Pishkalo，2008; Petrovay，2010）。 因此，太阳活动的预测对于改进电离层模型和其他应用以及对太阳行为的基本了解都很重要。
太阳黑子数（SSN）是用于估算太阳黑子周期（SC）的主要指标之一，是许多领域的重要参数，包括电离层研究（Sagir等，2015; Atici，2018; Kim，Kim）和Chang，2018; Sagir，Atici和Ozcan，2018; Sagir和Yesil，2018）。
由于基于该参数的时间序列的估计难度，重要性和潜在应用，它仍然是活动领域。已经提出了几种模型来估计SC参数（Layden等，1991; Thompson，1993; Dikpati，De Toma，和Gilman，2006; Kilcik等，2009; Pesnell，2008; Petrovay，2010; Pishkalo，2008， 2014）。在这些模型中，使用SSN时间序列值，其通常具有从1749年到2018年的太阳活动数据。因此，建模时间序列和预测未来对于实际生活中的许多领域是非常重要的。最近，在这个问题上已经做了大量的工作。文献中引入了许多重要的模型来准确有效地建模和预测时间序列。时间序列的重要性似乎看到了未来，特别是通过回顾过去。对于许多领域来说，未来的计划至关重要（Adhikari和Agrawal，2013; Raissi和Karniadakis，2018; Sirignano和Spiliopoulos，2018）。因此，时间序列广泛用于经济学，科学，商业和金融领域。
今天，在强大的计算机的帮助下使用不同的算法来估计时间序列。除了经典算法之外，机器学习（ML）和深度学习（DL）算法用于预测时间序列。 ML最重要的元素无疑是数据。通过使用作为ML原材料的大型数据集，可以比以前更好地掌握更复杂的现象。 ML的历史可以追溯到20世纪80年代，DL的历史可以追溯到20世纪60年代。然而，现有技术的DL算法已经使预测过程更进一步。本研究的目的是利用DL算法，利用1749年至2018年太阳黑子时间序列的月度观测数据，估算未来十年的SSN，本研究的主要贡献如下：

1. 基于1749年至2013年间的SSN数据进行了研究。本研究的目的是通过使用DL算法基于1749年和2018年之间的月度数据来估计太阳黑子数据的结果，并显示

2. DL算法在如此大的时间序列上的成功优于传统算法。使用R编程语言和库比较长短期记忆（LSTM），神经网络自回归（NNAR），ARIMA，朴素和季节性朴素算法的表现。

3. 在rsample（r语言的流行库）之一的帮助下，使用作为单变量时间序列的太阳黑子数据集的训练，测试和验证更加真实。

2. Background

在本节中，我们简要总结了有关时间序列的一般结构和特别是在研究中使用的算法的技术信息。 如果我们表达一个在时间t测量的案例（其中t可以是年度，季度，月度，每周，每日和每小时数据）并形成时间序列，我们可以简单地以yt形式显示它。 在开始时，t = 0，此时测量的有序事件，在t = t时，初始值和未来值可表示如下：

当在相同时间序列中回归时，时间序列中的每个yt值导致自回归模型，这取决于先前的值，例如yt-1。 我们可以在数学上表达这样一个模型：

在这样的模型中，前一次的响应变量是下一步的预测变量。 错误[_t]在简单线性回归模型中具有关于错误的通常假设。 自回归（AR）模型的程度取决于所用时间段中先前值的数量。 在这种情况下，等式2中的模型的程度是AR（1）。 如果我们想通过考虑前两年（即yt-1和yt-2）找到太阳黑子时间序列的预测，则二阶AR（2）模型可以表示为：

考虑前两个模型，以最一般的形式，t -1，t -2，t -3，…。。 ，t-k，k-阶可以表示为自回归模型AR（k）。 时间序列中两个值的系数之间的相关性称为自相关函数（ACF），其是测量在时间t观察到的值与先前值之间的关系的方法。 ACF可以显示为（Shumway and Stoffer，2011）

其中ACF仅使用值yt测量时间t-k时间序列的线性可预测性。 此外，部分自相关函数（PACF）方法用于确定自回归模型的顺序。

2.1. Long-Short-Term Memory (LSTM)

LSTM是一种特殊类型的递归神经网络（RNN），是深度学习（DL）算法之一。 它在众多任务中表现优于最先进的深度神经网络（DNN），特别是在语音和手写识别方面（Zazo等，2016）。 该算法由具有结构输入和输出的连续特殊单元组成。 获得通过LSTM单元进行的数据作为单元的输出数据，同时将其用作下一单元的输入数据。 在这方面，LSTM可以记忆比RNN更长的数据序列。 可以使用特殊门（通过使用三个乘法门单元：输入门，输出门和遗忘门）来销毁，过滤或收集每个单元中的数据以用于后续单元。 因此，基于Sigmoidal神经网络的门允许相应的细胞通过或破坏数据（Lewis，2016）。

2.2. NNAR Method in R

机器学习中最重要的工具之一，受到大脑结构的启发，人工神经网络（ANNs）是使计算机更具人性化的答案。它们允许对输入回归量和响应变量之间的复杂非线性关系进行建模。在时间序列模型中，时间序列的延迟值可以用作神经网络的输入，因为我们在线性AR模型中使用延迟值。这称为神经网络自回归（NNAR）模型。 NNAR模型是参数和非线性估计模型（Sena和Nagwani，2016）。这种模型用于R环境中，参数为p和k（NNETAR（p，k）作为前馈神经网络，具有滞后输入，用于预测单变量时间序列和单个隐藏层）。这里，p表示滞后输入，而k表示隐藏层中的节点数。例如，NNETAR（120,11）使用输入来模拟最后120个观测值（yt-2，yt-2，yt-3，…，yt-120），其中隐藏层中的11个神经元预测输出yt 。

2.3. Performance Metrics for Evaluation

为了通过使用太阳黑子时间序列数值来检查模型的性能，使用均方根误差（RMSE）（Adhikari和Agrawal，2013）。 它测量实际值和预测值之间的差异或残差。

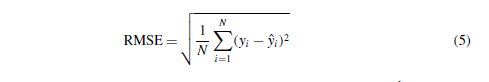
其中N是观察总数。 yi是实际值; 而ˆyi是预测值。 使用RMSE的主要优点是它可以处理预测时发生的极端错误。

3. Experimental Study and Analysis

本研究中进行的所有分析都是在R软件版本3.5.1（2018年7月2日）的环境中进行的，这是一种开源语言，免费且极其强大。请注意，此处报告的所有实验在SATA驱动器上安装的Windows 10 Pro操作系统上使用3.2 GHz CPU的PC Intel i5和8 GB RAM。本研究中使用的太阳黑子数量来自SILSO网站（www.sidc.be/silso/datafiles）的V2.0系列，作为月平均测量值（来自世界数据中心SILSO，比利时皇家天文台，布鲁塞尔的太阳黑子数据） 。
从SILSO网站以CSV格式下载的太阳黑子数据集中的数据由1749年至2018年之间的月度数据组成。所使用的数据属于270年的时期，包括总共3240个月的观察。在估算过程之前，在数据处理阶段，数据集中为零的非测量观测值与之前的稳健观测值保持一致，从而试图确保数据集的完整性。为了更好地改进预测并帮助理解时间序列，尝试使用分解方法将时间序列拆分为多个组件也很有用。测量中获得的数据的原始时间序列数据和分解图分别显示在图1和2中。基于数据结构，时间序列数据通常具有循环模式，其中观察在很长一段时间内上升和下降。
通过使用R中的分解方法，太阳黑子时间序列的三个分量如图2所示。图表底部显示的余数分量是从时间序列数据中减去季节和趋势周期分量时的残差 。如图2所示，SSN特征由正弦波趋势和变化方差组成。如图1和图2所示，由于数据集中的短期可变性以及长期不规则性，大量观察结果使得估计过程变得困难。

交叉验证（CV）方法用于使预测更加真实。利用该方法，在RStudio样本库的帮助下分析了3240个观测数据，该库使用滚动 - 起源 - 预测重采样方法。表1显示了太阳黑子数据集的6切片和12切片CV估计计划，其包括总共3240个月的观察。

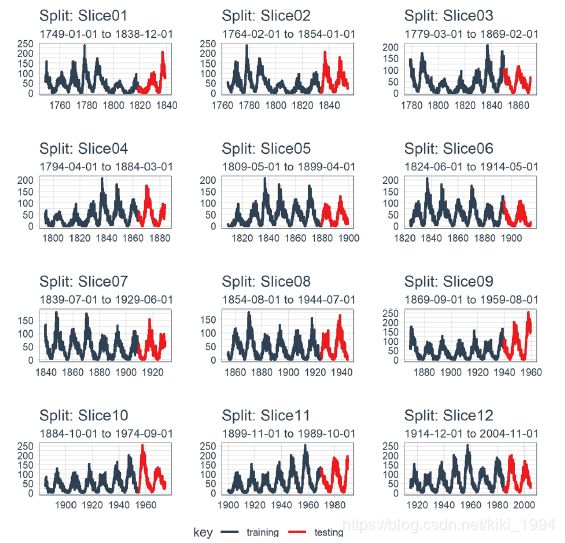
太阳黑子数据集的每个部分，在使用LSTM模型之前设置为12切片，被分为训练和测试两部分，如表​​1所示。此外，分配给训练的数据的三分之一是保留用于验证过程。在此阶段之后，数据集的每个部分都包含培训，验证和测试。同一表中显示的数据集的训练部分用于训练LSTM模型，验证部分用于设置LSTM超参数，测试部分用于测量LSTM模型的实际性能。具有训练的每个渐进切片和测试分裂的采样窗口如图3所示。
图3中12个独立数据中显示的太阳黑子数据集由来自1749年1月1日至1838年12月1日的第一个切片的数据组成，而第二个切片包含1764年2月1日至1854年1月1日范围内的数据。 slice从滚动数据集开始，称为skip-span。换言之，下一个切片比上一个切片先180条开始记录。跳过跨度是基于12切片的模型的180条记录和基于6条切片的计划的240条记录。

3.1. LSTM Model Parameters

为了提高LSTM算法的性能，在R的配方包的帮助下缩放了培训，验证和测试数据。如果在机器学习的支持下训练的数据很大，那么一次训练现有数据可能不会在性能方面给出好的结果。不是将数据集用作单个部分，而是优选将其划分并使用多个部分。
在这项研究中，相同的策略适用于太阳黑子数据集。如表2所示，对于首先分为6个部分的太阳黑子数据集，分别使用1200,600和10的训练，测试和批量大小。因此，训练和测试迭代次数分别计算为120和60。由于DL算法使用梯度下降算法来优化他们自己的模型，因此通过训练数据集来不断更新权重以实现更准确的估计。因此，为了更好地训练LSTM模型，使用的纪元值为100。

3.2. Results

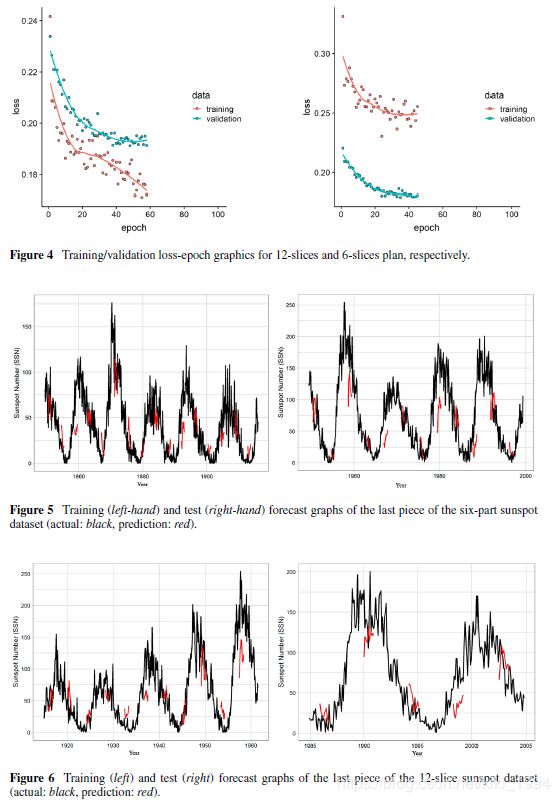
使用以两种不同方式配置的太阳黑子数据集来执行LSTM模型的训练，验证和测试。首先，在使用LSTM模型训练和测试6切片数据集的最后部分之后，将相同的过程应用于12切片数据集的最后切片。如图4所示，6件式滚动原点预测采样模型的损失低于重采样模型的12件滚动原点预测。
此外，由于6切片滚动原点预测出现在重采样模型（左）上，系统已经在大约60个时期停止了训练过程，因为验证损失保持不变。我们还可以说训练性能优于验证性能，如左图所示。
对于6切片和12切片模型，训练和测试的最后切片的预测分别显示在图5和6中。在图5和图6中，模型在训练和测试数据上的性能在实时周期的帮助下以图形方式显示。以一定间隔显示的红线在视觉上呈现训练（左）和测试（右手）估计的性能。很明显，使用两个模型计划中的训练数据的估计结果比测试结果更成功。
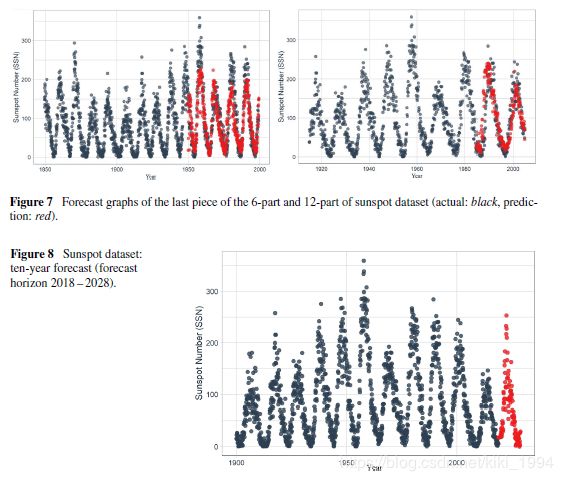
在图7中，太阳黑子数据的6部分和12部分方法的最后部分的RMSE测试值彼此接近，但是6部分方法显示出更好的预测性能。 6部分和12部分估计的RMSE测试值分别为35.9和36.9。
使用LSTM模型，对6段太阳黑子数据集的每个部分进行训练，验证和测试。 在培训，验证和测试过程结束时，接下来的120个月，换句话说，进行了十年（2018 - 2028）预测，如图8所示.LSTM模型用于估计时间间隔 在2018年至2028年间，太阳黑子数据集包含从1749年到2018年的3240个观测数据，涵盖270年的时期。

LSTM模型使用Keras模型序列函数创建，该函数由线性堆叠层组成。在该研究中，使用两个LSTM层，每个层由50个单元组成。第一个LSTM层用于输入。模型条目分别包括时间步长和许多特征。第二个LSTM层定义为第一层。在第二LSTM层中，返回2D数据形状，同时从第一LSTM层返回3D形状。在编译模型时，adam被用作优化器。作为优化算法，adam可用于基于训练数据迭代地更新网络权重。它需要相对较低的内存，即使只需稍微调整一下超参数，通常也能正常工作。在同一模型中，mae metric，平均绝对误差（mae）是两个连续变量之间差异的度量，因为使用了损失。在这里，我们使用DL方法从2018年开始进行下一个十年的SSN预测。在LSTM模型的帮助下，我们已经显示了像太阳黑子这样的非常大的数据集的成功结果。我们还看到时间序列的交叉验证方法显示了更令人满意的结果。

在R环境中，它是统计计算和图形的语言，我们使用Mean，Naïve，Seasonal Naive，Drift，ARIMA和NNAR模型来预测太阳黑子数据集，如图9所示.LSTM DL模型的太阳黑子数据集以两种不同的方式建模，首先是6件，然后是12件。为了计算每种方法的平均RMSE，计算6部分方法的平均值（六种不同的RMSE值）。然后计算12部分方法的平均值（12个RMSE值）。为了使用该方法，我们在LSTM模型中使用并因此实现更真实的结果，我们将太阳黑子数据集分成12个单独的部分，这些部分每月获得并包含3240个记录。作为分割过程的结果获得的每个数据集部分包含540个记录。在这里，我们使用所研究的时间序列的最后部分研究了经典模型。在540条记录中，90％用于培训（486条记录），其余10％（54条记录）用于测试。作为本研究中使用的算法的训练结果，算法测试程序的RMSE值如表3所示。
如表3所示，性能最佳的算法是LSTM 6部分方法，LSTM 12部分方法，NNAR和ARIMA，RMSE值分别为35.9,36.9,42.41和45.60。应用于太阳黑子数据集的NNAR模型的测试结果和使用NNAR模型的未来十年预测显示在图10和11中。

3.3. Comparison with Other Studies

3.3.1. Comparison of Analysis Results in Terms of Statistical Accuracy

Siami-Namini和Namin（2018）使用不同的数据集比较了LSTM和ARIMA模型。他们发现ARIMA和LSTM的RMSE平均值分别为511.481和64.213。在同一项研究中，他们表明LSTM模型表现更好。比ARIMA模型。我们同意Siami-Namini和Namin（2018）的观点，即LSTM模型比经典模型表现更好。 Maleki等人。 （2018）比较了ARIMA和NNAR模型的性能，并表明NNAR模型的表现优于ARIMA模型。 Dancho（2018）试图通过在太阳黑子数据集中使用LSTM来预测未来十年，该数据集包含R数据集中1749年至2013年之间的月度数据。根据1749年至2013年间的太阳黑子数据集，发现测试数据的RMSE约为26.91，包含265年（3177条记录）。然而，我们研究中的数据涵盖1749年至2018年，为期270年，包含3240条记录。使用的两个数据集之间存在五年的差异;换句话说，60个月。他们使用R数据集库中的就绪和已处理数据。但是，我们已经从SILSO站点下载了太阳黑子数据集。因此，我们尝试使用我们研究中的最新数据。考虑到上述两个数据集之间的差异，预计RMSE值将不同。在从SILSO站点下载的太阳黑子数据中，一些测量值为零。这些值保持与先前测量值相同。在本研究中，我们使用了LSTM和NNAR模型，这些模型表现出比ARIMA和Naive模型更好的性能。

分析问题和解决问题的方法论方法与Maleki等人的方法非常相似。 （2018）。 Shaikh等人。 （2008）在傅里叶变换技术（FFT）的帮助下，使用1818年至2002年之间的太阳黑子数据集进行了分析。 Chattopadhyay和Chattopadhyay（2012）使用ARIMA和一个自回归神经网络（AR-NN）模型来预测1992年至2008年的太阳黑子时间序列。对于太阳黑子时间序列的同质性测试，他们使用Pettit测试，Mann-Kendall测试趋势，以及正常分布的Kolmogorov-Smirnov检验。在他们的主要结论中，他们表明AR-NN（3）模型比ARMA（3,1）和AR（3）模型具有更好的性能。 Gkana和Zachilas（2015）使用平均互信息（AMI）和假最近邻（FNN）方法来估计1749年至2013年间每月太阳黑子时间序列的合适嵌入参数。他们使用神经网络型核心算法来预测2013年 - 2014年间隔。

我们简要总结了使用与上述几乎相同的数据集的工作，特别是在我们的研究中。我们的研究基于1749年至2018年的SNN数据。对于每天增加新记录的不断增长的数据集，例如太阳黑子，使用DL算法进行十年预测更为有利。

3.3.2. Comparison of SSN Forecasts

Rigozo等。 （2011）进行了一项研究，根据光谱成分的外推估算太阳周期24和25的太阳活动强度。他们估计第25周期的太阳黑子最大数量将发生在2023年4月，太阳黑子数量为132.1（太阳周期长度为118个月或9。8年）。在同一项研究中，还估算了太阳周期24，并且2013年11月的最大SSN值预计为113.3。但是，当检查实际的SSN值时，2014年2月达到SSN值的最大SSN值。 146.1。因此，可以说Rigozo等人。 （2011）达到其最大SSN估计，与实际SSN值偏差约30％，因此估计方法是好方法。
在一项类似的研究中，Quassim，Attia和Elminir（2007）使用神经模糊方法估算了SC 24和25的振幅和地磁活动。因此，他们表示太阳能周期24将达到最大值，2011年SSN为110，太阳周期25将达到最大值，2021年SSN为116.他们的估计与太阳周期24的实际情况不一致，因为太阳周期24的最大SSN是2014年2月。同样，可以说，对于Solar Cycle 25，他们的估计可能不可靠。
在另一项研究中，Okoh等人。 （2018）使用称为混合回归 - 神经网络的方法，其结合回归分析和神经网络学习来估计SSN。他们预测太阳活动周期24的结束时间为2020年3月（±7个月），SSN为5.4，太阳活动周期25的最大值为2025年1月（±6个月），SSN为122.1（±18.2）。 Kane（2007）预测太阳周期25的最大振幅在2022年到2023年之间将介于112和127之间（平均119）.Penn和Livingston（2011）发现太阳黑子磁场强度下降，确定了未来趋势，并得出结论，太阳周期24的SSN值将达到峰值66左右，太阳周期25将比太阳周期24弱，SSN为59.但是，可以看出周期24的估计不正确，因此它可能不适用于第25周期。
Hiremath（2008）预测SSN在Cycles 24和25最大值时为110，活动将在第26周期增长.Javaraiah（2008）发现第25周期比第24周更强大.Nielsen和Kjeldsen（2011年） ）得出结论，第25周期将比周期24弱。使用Neuro-Fuzzy模型，Attia，Ismail和Basurah（2013）发现第25周期将更弱，最大SSN将在2022年出现，峰值为90.7± 8。 Pishkalo（2008）通过检查SC 1 - 23的不同参数之间的关系来估算SC 24和SC 25.他表示SC 24将在2012年4月至6月达到最大振幅110.2±33.4，下一个最小值将是在2018年12月 - 2019年1月，SC 24将大约11。1年，SC 25将在2023年4月至6月达到最大振幅112.3±33.4。此外，Pishkalo（2014）估计SC 25将略强于SC 24最大SSN为105-110.Sabarinath和Anilkumar（2018）预测SC 25将弱于SC 24，最大SSN将为75-95.Li，Feng和Li（2015）表示SC 25 SSN为109.1，将于2023年10月达到最大值。最近，Sarp等人。 （2018）使用非线性方法预测SC 25。他们预测SC 25最大值将出现在2023.2±1.1，峰值SSN为157±12。在我们的研究中，估计太阳周期25的最大值将达到2022年7月的峰值SSN为167.3和周期25将持续大约十年。这一结果意味着第25周期将比第23周期和第24周期更强。所得结果与Pishkalo（2008），Rigozo等人的研究结果一致。 （2011年），Pishkalo（2014年），Sarp等人。 （2018），和Okoh等人。 （2018），因为所有人都认为第25周期比第24周期更强。

4. Conclusions

在本研究中，通过DL算法进行了11年期间太阳活动变化的预测，DL算法是机器学习的子领域。尽管在文献中有关于太阳周期预测的机器学习的研究，但是使用NNAR和LSTM深度学习算法对太阳周期25进行SSN预测，使用从1749年到2018年的SSN的月平均值.SSN估计是也是用经典模型制作的，如ARIMA，Naive，Seasonalnatïve和drift。然而，发现NNAR和LSTM深度学习模型更适合SSN估计。在一些关于周期25预测的研究中，发现该周期的幅度小于周期24，并且一些周期大于周期24.在该研究中，预测周期25将具有比之前更大的幅度。周期。还预测周期25的最大振幅将在2022和2023之间达到，如先前的一些研究所示（例如Kane，2007; Rigozo等，2011; Attia，Ismail和Basurah，2013; Sarp等。 ，2018）在文献中。
如前所述，预测太阳活动的变化对于与太阳有关的所有系统都至关重要。因此，考虑到机器学习的使用领域不断增加，本研究将成为机电学习在电离层研究中更广泛应用的重要一步。
披露潜在的利益冲突 作者声明他们没有利益冲突。
出版商的注释 Springer Nature在已发布的地图和机构关联中的管辖权声明方面保持中立。